基于遗传算法的护理机器人逆运动学求解方法
2022-11-09张立博李宇鹏朱德明付永领
张立博 李宇鹏 朱德明 付永领
(北京航空航天大学 机械工程及自动化学院, 北京 100083)
由于全球老龄化日益严重,未来老年人的护理问题变得十分严峻,随着现阶段人工智能技术的发展,护理机器人投入医疗护理领域,可以减轻护理人员负担,提高护理人员的工作效率,一定程度上可以解决护理对象的自理能力[1]。 护理任务中,护理机器人工作需要双臂和腰部的协调操作才能将病人抱举,而且所处的环境一般比较复杂,抱起沉重的病人很容易发生二次伤害[2]。
护理机器人系统存在着多变量、强耦合、高阶及非线性等特性,这些特性使得对护理机器人的逆运动学精确求解变得非常困难[3],特殊的结构没有非常满意的传统解法,各种算法根据自身的特点去解决特定结构形式的机器人[4-5]。 对于串联机器人来说逆运动学解比较复杂,根据结构的复杂程度不同求解难度也不同,基本原理都是根据结构参数,由机械臂末端位姿矩阵求解各关节的转动角度值[6-7]。 特定的结构可以采用现有方法直接求解,如三轴交于一点的结构一般用PIEPER 法进行研究[8-9]。 Pieper[10]证明了当机器人有3 个相邻关节轴相交于一点时,一定存在解析形式的逆解。 Duffy[11]证明了当3 个相邻的关节轴互相平行时,也一定存在解析形式的解。Goldenberg 等[12]提出了一种基于新的快速收敛约束非线性优化算法,适用于任意自由度的旋转或棱柱关节机器人。 Ayusawa 和Nakamura[13]提出了一种快速逆运动学算法,先将残差视为外力并分布到每个环节再利用牛顿-欧拉递推算法从静态平衡点计算梯度。 Manocha 和Canny[14]提出了一种通用六自由度机械臂的高效逆运动学算法及其实现,利用系统的代数性质通过降阶来计算特征值问题。 护理机器人结构复杂,而且大小臂轴线相错,几何结构不满足PIEPER 准则,代数法和几何法不能很好解决逆运动学解问题。 遗传算法的隐含并行性,让其在搜索过程中具有实时性,从而能够快速地找到合适的解[15]。 针对遗传算法在实际应用中出现早熟收敛和局部搜索能力较弱的缺点,文献[16]在简单遗传算法的基础上改进了交叉变异算子,改进了适应度函数排序方法;文献[17]通过改进交叉、变异算子自整定策略和精英策略,提高了算法的收敛速度;文献[18]通过优化选择算子和变异算子提高了算法搜索速度并保证全局最优性,具有更快的搜索速度和全局最优性。
为了解决护理机器人手臂末端位姿误差较大的问题,本文在分析结构约束关系的基础上,基于遗传算法提出了护理机器的腰臂耦合逆解算法,对解进行了合理的规划,使求解过程更为精确。
1 正向运动学分析
护理机器人正向运动学分析是遗传算法求解逆运动学的基础,需要依据正运动学和机器人末端位姿坐标系对逆运动学进行求解。
1.1 护理机器人结构
本文研究的护理机器人为移动式仿人双臂机器人,实体样机如图1 所示,由4 个全向轮、底盘框架、腰部、双臂和手掌部分组成,具有轮式机器人和双足机器人的优点。 采用全向轮的底盘,灵活便于控制,稳定性良好,与躯干机械臂组合成复合式机器人系统,既增加了护理机器人的灵活使用性,又拓展了其工作范围。 护理机器人共有15 个自由度,为高阶非线性耦合系统,底盘具有3 个自由度可实现整体纵、横和回转运动,腰部1 个俯仰自由度和1 个侧倾自由度,每条手臂有5 个自由度。

图1 护理机器人样机Fig.1 Nursing robot prototype
1.2 连杆坐标系的建立
首先,为每个杆件建立相对的参考坐标系,确定从一个坐标到下一个坐标的变换步骤。 然后,从基座的第一个杆件依次变换结合起来,得到机器人的总变换矩阵,建立最终的运动方程,从而求解机器人的位姿。
根据D-H 连杆坐标系建立机器人运动学模型,固连在连杆i上的固连坐标系称为{i},关节轴i-1 和关节轴i之间公垂线的长度为ai-1即连杆长度;夹角为αi-1;公垂线ai-1与关节轴i的交点到公垂线ai与关节轴i的交点的有向距离为连杆偏距di,ai-1的延长线和ai之间绕关节轴i旋转所形成的夹角为关节角θi。 图2 为护理机器人各连杆的连杆坐标系,腰部关节的自由度分别为俯仰关节转角θ1和侧倾关节转角θ2,左臂各关节的转角分别为θl3、θl4、θl5、θl6和θl7,右臂各关节的转角分别为θr3、θr4、θr5、θr6和θr7。

图2 护理机器人各连杆的连杆坐标系Fig.2 Linkage coordinate system of each linkage of nursing robot
考虑护理机器人初始状态各肢体的相对位置,基于D-H 模型,可以得到护理机器人运动学的连杆参数,如表1 所示。
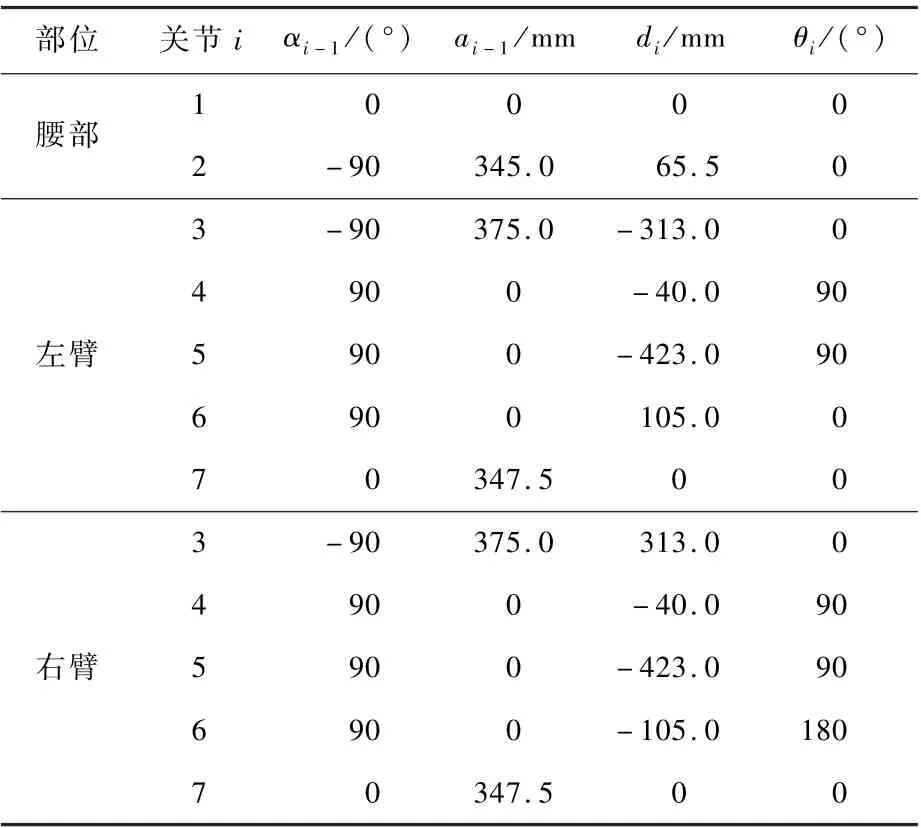
表1 护理机器人运动学连杆参数Table 1 Nursing robot kinematic linkage parameters
根据连杆坐标系模型的连杆参数计算出连杆的变换矩阵,从基座到末端把相应的连杆变换矩阵依次相乘得到坐标系{N}相对于坐标系{0}的变换矩阵:

2 个杆件的坐标系在世界坐标系中相互变化时,在坐标系没有相对运动的情况下,通过2 次平移和1 次旋转后2 个坐标系可以重合。 建立各杆件相对应的齐次坐标变换矩阵,并将其定义为T矩阵。
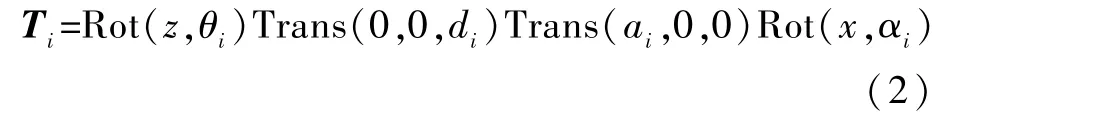
其变换矩阵为
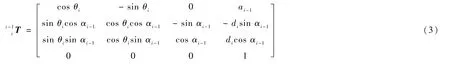
建立护理机器人各杆件相对应的齐次坐标变换矩阵,得到护理机器人的正运动学方程为
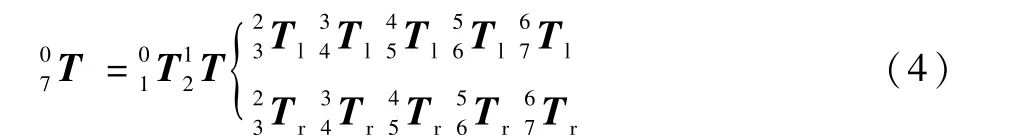
通过对双臂结构的分析可以将主体结构分解为具有对称结构的独立单臂在前2 个关节处重合形成的耦合结构。 分解后的左右机械臂末端的手腕坐标系在世界坐标系中的位置和姿态为
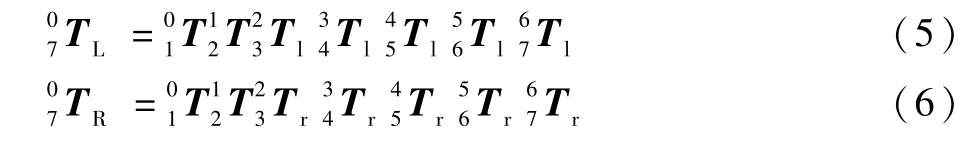
1.3 正运动学的仿真
护理机器人的运动学模型通过MATLAB 中的机器人工具箱得到运动过程的位姿图,输出的位姿矩阵可以用来验证所建立的机器人运动学模型的有效性和正确性。
将机器人初始状态的各关节转角值代入式(5)和式(6)中,利用MATLAB 的矩阵计算分别计算出机械臂的末端手腕关节的位姿矩阵为

将模型参数代入Roboticstoolbox 工具箱,通过工具箱的程序得到最终的位姿。 在MATLAB中对设计的机器人进行连杆模型简化,对正运动学求解过程进行编程,仿真结果如图3 所示。

图3 机器人在MATLAB 中的模型Fig.3 Robot model in MATLAB
利用函数fkine 得到的正运动学的解与运动学方程得到的初始状态末端手腕关节的位姿一致,证明本文所列运动学方程是正确的。
2 标准遗传算法的逆运动学解
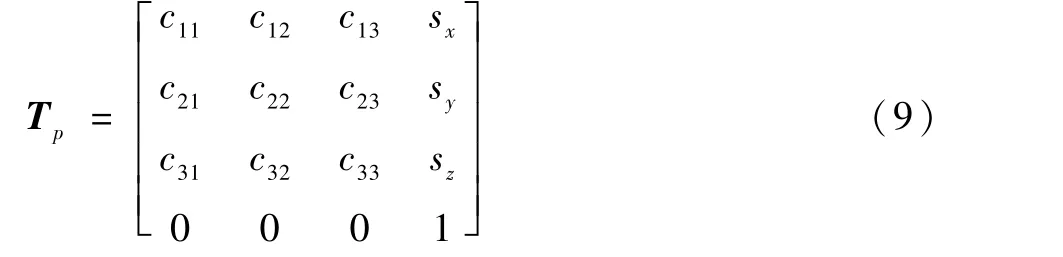
遗传算法求机器人逆运动学问题的首要任务是确定遗传算法的目标函数,以分解的左臂为对象,若P点是机械臂末端腕关节可达空间的一点,则点P对应的当前位姿矩阵Tp为
机器臂末端关节在直角坐标系中的目标位姿矩阵Te为
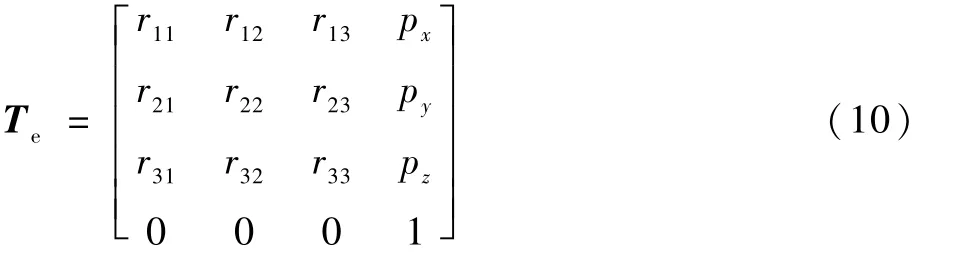
机械臂通常根据机器人末端目标位姿和当前位姿的差值作为整体优化条件来计算适应度的大小。 式(9)和式(10)为齐次变换矩阵,左上角3 ×3矩阵是机械手臂末端的姿态矩阵,此矩阵是一个单位矩阵,右上角3 ×1 列向量为机械手臂末端腕关节的坐标系原点位置向量。 根据机器人位姿矩阵的表示方法,目标位姿矩阵和当前位姿矩阵的差值可写成

式中:ΔP为位置向量差值;ΔO为姿态矩阵差值;关节变量θ(θ1,θ2,…,θ7)为遗传算法的种群个体,则目标函数为
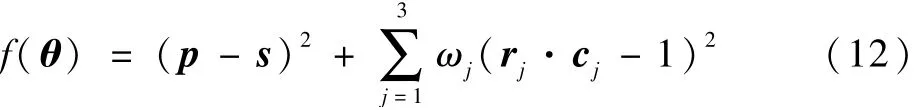
式中:p和s分别为目标位姿矩阵和当前位姿矩阵的位置列向量;r和c分别为目标位姿矩阵和当前位姿矩阵的姿态矩阵;ω为条件系数,当末端无方向要求时,ω=0,当末端有方向要求时,ω=1,由于护理机器人工作时需要调整末端姿态,取ω=1。 对于护理机器人逆运动学的遗传算法,适应度函数为

利用标准遗传算法进行最小值优化,设置遗传算法参数后在计算机中进行仿真实验。
经过50 次迭代后,种群中个体的目标函数值分布如图4 所示。 可以看出,初始种群个体的目标函数值分布比较集中,容易产生局部最优。
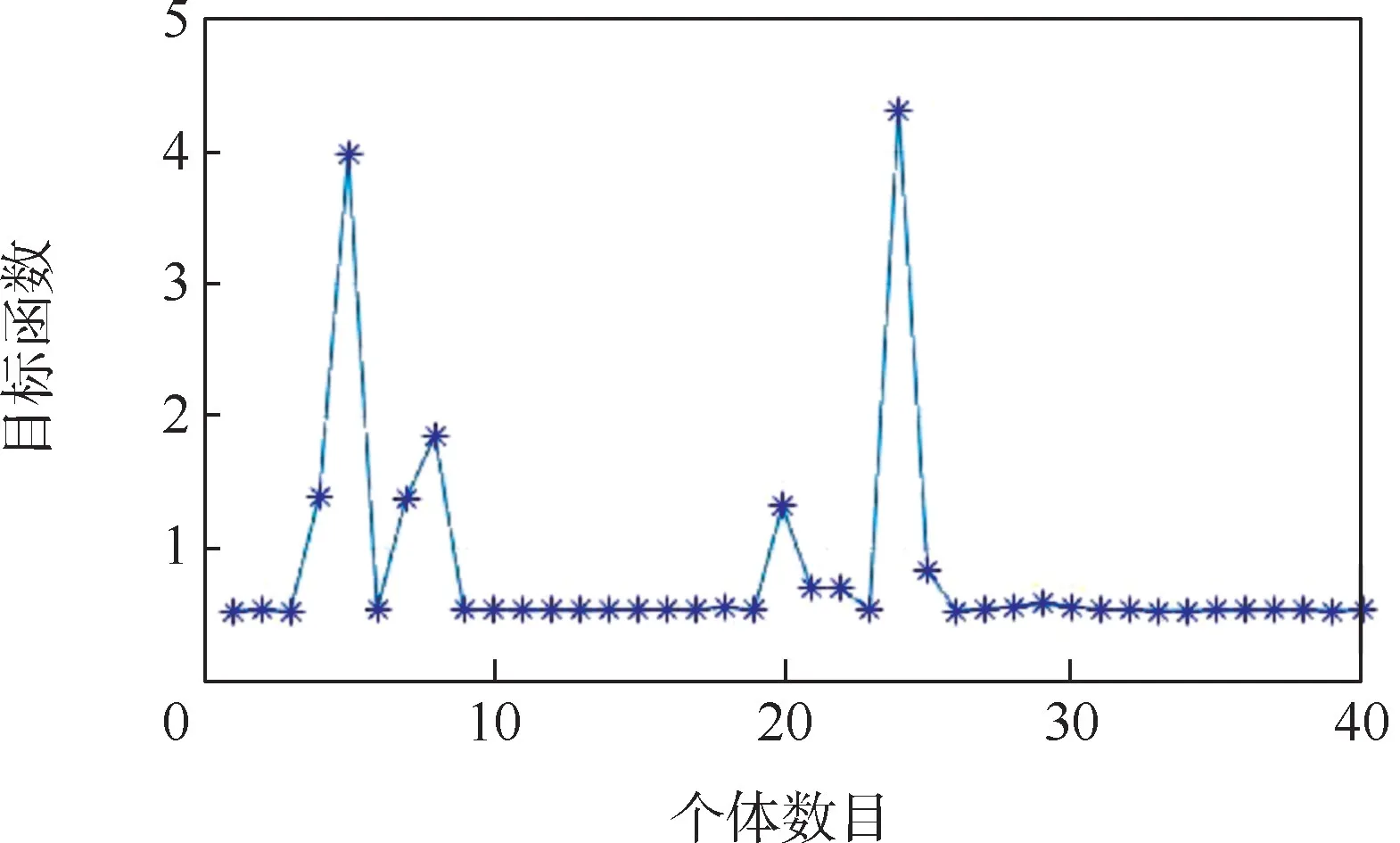
图4 种群中个体的目标函数值分布Fig.4 Distribution of objective function values of individuals in population
种群适应度函数均值和最优解随遗传代数的变化如图5 所示。 可以看出,遗传算法的适应度函数和有效逆解基本收敛,但最终收敛值不是理想的0,而是从第10 次迭代后就过早停止了向全局最优解进化,停滞在0.532 2 左右。
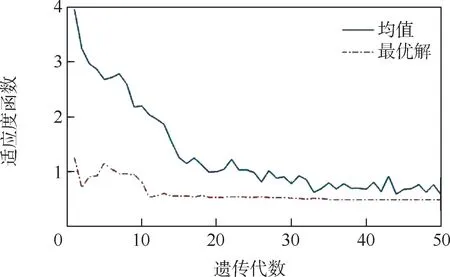
图5 种群适应度函数均值和最优解的变化Fig.5 Variation of the mean value of population fitness function and optimal solution
关节空间遗传算法优化解位姿如图6 所示。可以看出,标准遗传算法所得到的最优逆解和目标位姿存在误差,误差对应到有效逆解结果的位姿图示上可以看出,机器人手臂末端点没有达到目标位姿的目标点。

图6 关节空间遗传算法优化解位姿Fig.6 Genetic algorithm optimization of pose in joint space
护理机器人手臂关节较多,设定的基本种群规模相对较小,而且适应度函数值较大使得有效逆解不易被选取。 此外,适应度函数以位姿偏差为核心,机器人运动到不同状态时所处位置的位置偏差和姿态偏差变化方向不一致,个体很容易被淘汰,因此需要进一步优化。
3 标准遗传算法的改进算法
针对标准遗传算法的不足,从增加群体多样性和适应度函数标定2 个方面对标准遗传学算法进行适当改进,解决原始算法收敛速度慢和收敛精度低等问题,提高护理机器人逆运动学解的精度。
3.1 初始种群的产生
护理机器人关节转角范围相差大,且极其不均匀。 因此,在增加种群的基础上采用等分区间的方法来产生初始种群,即将各个关节的转角范围等分成相等的5 个小区间,再在每个小区间随机生成20 个个体,最后5 个小区间的所有个体一起来组成初始种群。
每个关节的运动范围的表达式为
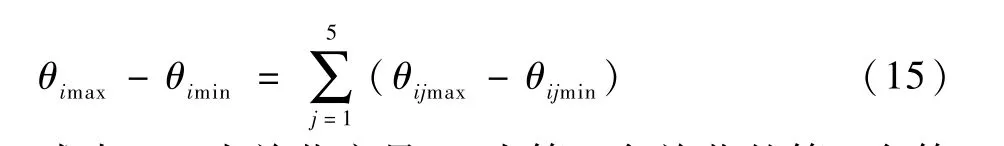
式中:θi为关节变量;θij为第i个关节的第j个等分区间。
关节运动范围等分区间如图7 所示,θ3的转角范围为π/4,θ5的转角范围为π。

图7 关节运动范围等分区间Fig.7 Joint range of motion equipartition interval
以θ3和θ5采用等分区间的方法前后产生初始种群的个体分布,如图8 所示。 可以看出,采用等分区间的方法所产生的个体分散程度比整体随机种群个体的分散程度高。

图8 等分区间前后个体的分布Fig.8 Distribution of individuals before and after equipartition interval
因此,采用等分区间后不仅增大初始种群包含最优解组合概率,而且避免了个体的不均匀分布,提高了搜索效率。
以等分区间方法产生的初始种群进行遗传算法求解最优解,其他参数设置基于标准遗传算法,运行算法得到适应度函数均值和最小值随代数的变化,如图9 所示。 可以看出,最优解在30 代是基本收敛到最小值,虽然没有得到较小的解,但延长了进化代数,推迟了早熟进程,提高了算法的可靠性。
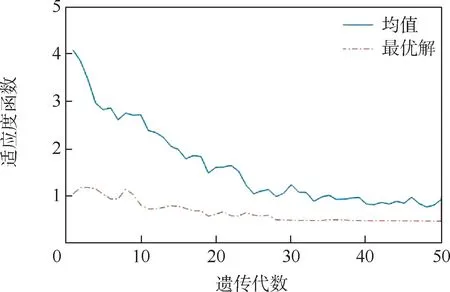
图9 等分区间种群适应度函数均值和最优解的变化Fig.9 Variation of the mean value of population fitness function and optimal solution in equipartition interval
3.2 适应度函数的选择
随机产生的种群适应度值较大的个体统治着整个初始种群,进化到最优个体之前停止进化,以至于无法产生全局最优解。 进化过程中个体适应度的值基本不变,造成了获得的最优解不是全局最优解。 为了解决该问题,通过反复地对比与运算,在适应度函数中加入了可变权因子β,随迭代次数基于位姿误差的最小可变权因子,改进后适应度函数的计算式如下:
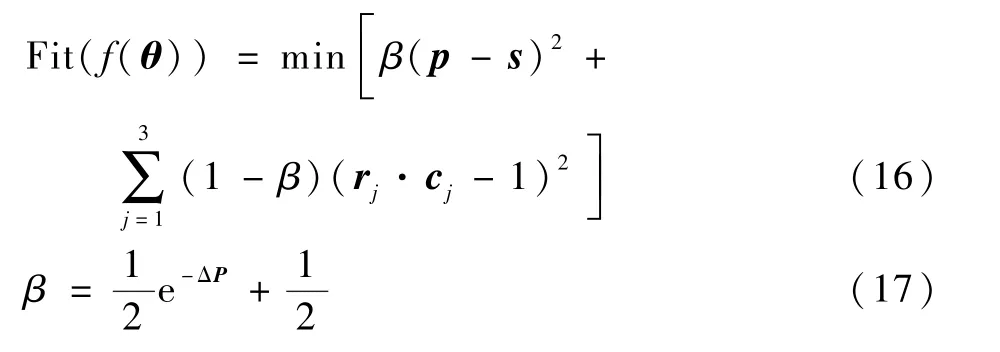
在进化开始时位置误差和姿态误差应分配相同的权重,初期位置误差较大,而姿态误差变化一直较小,因此可变权因子β表达式为式(17)。 在迭代进化过程中,β随着ΔP的改变而改变,ΔP的值在算法开始时一般比较大,此时β值接近于0.5;随着进化过程的继续进行,到了一定的代数以后,ΔP值逐渐变小,而β接近于1。 加入可变权因子β后的适应度函数,可以为位置误差和姿态误差在进化过程中分配合适的权重,确保了进化过程向全局最优解的方向进行收敛。
3.3 改进算法的仿真分析
在标准遗传算法运动学逆解程序的基础上,按等分区间划分产生种群,并且使用加入变权因子的适应度函数,进行仿真分析。 经过50 次迭代后,种群中个体的目标函数数值分布如图10 所示。 可以看出,个体的目标函数值分散程度高,保证了种群的多样性。
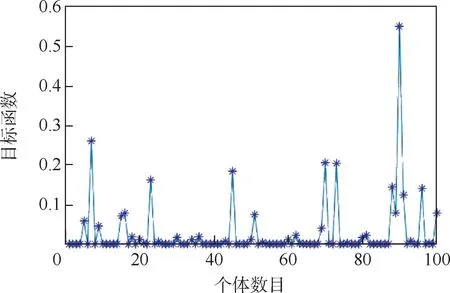
图10 改进算法种群中个体的目标函数值分布Fig.10 Distribution of objective function values of individuals in population of improved algorithm
种群适应度函数均值和最优解随遗传代数的变化如图11 所示。 通过算法改进前后的变化对比可以看出(见图5 和图11),在经过10 次迭代后,改进算法开始快速收敛于全局最优解,且适应度函数均值和最优解的函数值趋近于0,收敛精度高,可以得到精确的最优解。
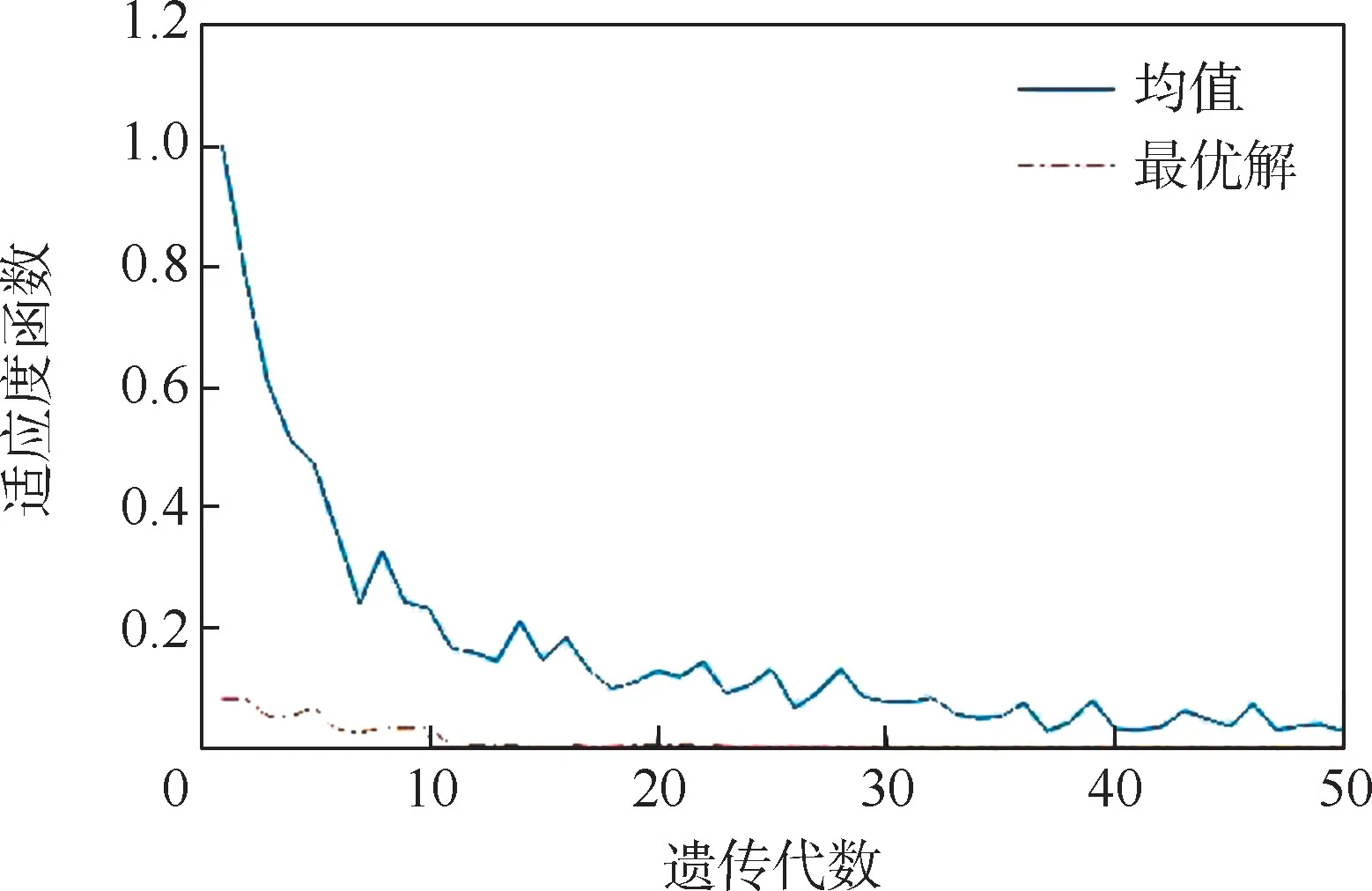
图11 适应度函数均值和最优解随遗传代数的变化Fig.11 Variation of the mean value of fitness function and optimal solution with number of genetic generations
关节空间遗传算法优化解位姿如图12 所示。对比图6 可以看出,目标位姿和当前位姿基本重合,误差很小。

图12 关节空间改进算法优化解位姿Fig.12 Optimization of pose in joint space using improved algorithm
改进遗传算法可以有效解决机器人运动学逆解,为护理机器人手臂的运动学逆解算法提供了一种新的思路,也可为实现机器人智能运动规划提供参考。
4 实验验证
在实验室环境中,搭建三坐标测量系统对护理机器人末端姿态进行测试。 通过摄影测量实现姿态的精准测量。 图13 为测试系统实物图,包含数码相机、测量光笔、工控机及软件系统。

图13 三坐标测量系统Fig.13 Three coordinate measuring system
通过测量光笔的位姿来间接测量护理机器人手臂的末端姿态位置,光笔的测量精度决定了测量准确性。 采用CLP 6800 的光笔,其测量精度为±0. 03 mm,工作温度0 ~45℃,可以满足系统需求。 图14 为测试实验图,操作人员手持光笔,在数码相机的有效拍摄范围内,对目标点进行测量,光笔外侧的LED 要指向数码相机。

图14 测量实验Fig.14 Measurement tests
以护理机器人水平抱举姿态为目标位姿点,对应的左臂末端位姿矩阵为

基于改进遗传算法求得的最优解InvsolL 为[0.444 6 -0.087 7 0.674 2 1.573 3 1.860 3-0.305 1 -0.162 9]。 护理机器人根据运动学逆解到目标位置后,对目标点进行测量。 测量得到的左臂末端的位姿为

对比分析其位姿误差ΔE,其中位置误差ΔP为末端执行器坐标系原点的位置向量与目标点位置向量差的模的平方:
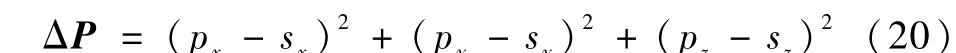
姿态误差ΔA为护理机器人末端执行器坐标系各个坐标轴向量与对应目标点坐标轴向量差的模减1 的平方:
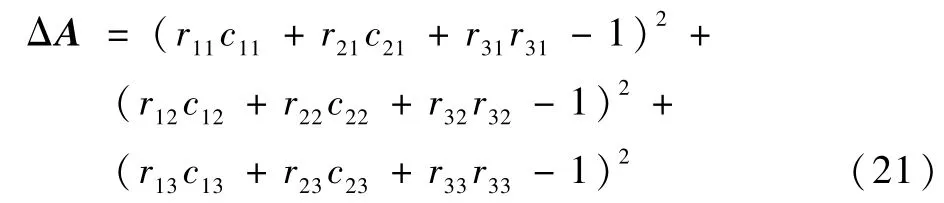
计算可得到左臂末端位置的位姿误差ΔEl为0.886 ×10-3m。 实验中右臂和左臂的运动一致,因此主要对左臂进行分析和实验。
从计算结果可以看出理论目标位置和测量目标位置之间存在一定的误差,但对于主要抱取病人的护理机器人来说,误差在允许的范围内。
5 结 论
1) 本文采用等分区间法产生的初始群体不仅增大了包含最优解组合的概率,而且避免了个体的不均匀分布,提高了搜索效率。
2) 在适应度函数中加入基于位姿误差的最小可变权因子,确保了进化过程向全局最优解的方向进行收敛。
3) 通过搭建实验测试系统,结果表明改进后的遗传算法求得的逆向运动学解为最优全局解,护理机器人的位姿误差较小。
