函数型正则广义典型相关分析
2022-11-09王志超TENENHAUSArthur王惠文赵青
王志超 TENENHAUS Arthur 王惠文 赵青
(1. 中国工商银行 博士后科研工作站, 北京 100032; 2. 法国高等电力学院 信号处理与电子系统系, 吉夫伊维特 91192;3. 北京航空航天大学 经济管理学院, 北京 100083;4. 北京航空航天大学 复杂系统分析与管理决策教育部重点实验室, 北京 100083)
Abstract: An effective dimension reduction method for multivariate functional data is developed within the theoretical framework of regularized generalized canonical correlation analysis. Functional data in square integrable spaces is first projected in an integral form to a series of numeric variables, and those variables are then used for simultaneously determining the related projection directions of functional features by maximizing a kind of global correlation measure, which achieves the featured information extraction and rapid dimension reduction of multivariate functional data as traditional numeric variables. A general basis function system is used to create the iterative computing algorithm for the optimal functional projection weights, which is independent of the specified basis functions. A large number of simulation results for infinite samples show that the proposed method is able to detect the correlation among multivariate functional data and obtain consistent estimates for the associated functional projection weights. The real-data study on the gait of Parkinson’s patients indicates the interpretability of the numeric featured information derived from the original functional data and the utility of the proposed method.
Keywords: functional data; regularized generalized canonical correlation analysis; feature extraction;functional principal component; gait of Parkinson’s syndrome
随着传感器、硬件存储等信息技术的快速发展,数据信息的获取得到极大便捷,可供使用的数据资料不再局限于传统单点型数值变量,而具有复杂多样的表现形式和内在特征。 作为新兴复杂数据类型之一,函数型数据描述一类指标变量随时间、空间等因素连续变化的曲线[1],被广泛应用于众多研究领域[2-7]。 例如,对于压力传感器实时监测的记录,以及高频变动的股票日内价格和收益率,这些指标应当认为是连续变化的,而不仅仅是若干时间点观测的离散数值。 曲线的无穷维特征,成为函数型数据分析(functional data analysis, FDA)需要解决的关键问题;因此,许多对于函数的等价表达方法被陆续提出,如基函数展开和重生核表示等[8]。
在日趋复杂的应用场景中,往往需要同时考虑2 个甚至更多函数型变量之间,或函数型变量与数值变量之间的关系。 面对数据多样化引发的高维问题,需要对多元函数型数据进行降维处理;对此,一种有效的解决方法是:从函数型数据中提取一系列蕴含原函数特征信息的数值变量用于后续统计建模。 按照这一思路,Ferre 和Yao[9]提出基于切片逆回归(sliced inverse regression, SIR)的函数型数据充分降维方法;Wang 等[10]进一步提出函数型SIR 方法的稳健估计;Reiss 和Ogden[11]则通过函数型主成分回归和函数型偏最小二乘(partial least squares, PLS)方法确定函数型数据的展开表示。
现有研究主要根据函数型数据变量内部变化信息或模型设定实现特征信息的数值化表达,当变量个数较多时,逐一进行特征信息提取不仅效率低下,且无法建立不同函数曲线之间的联系。基于SIR 和PLS 的方法虽然考虑了两两函数型变量之间的相关关系,但很难适用于更多变量的情形。 Tenenhaus 父子[12-14]提出的正则广义典型相关分析(regularized generalized canonical correlation analysis, RGCCA)将众多分块数据分析方法进行推广统一,得到许多推广和应用[15-18]。
为了实现多元函数型数据的特征信息提取及快速降维过程,本文在FDA 框架下,考虑函数型RGCCA(functional RGCCA, FRGCCA)。 具体来说,FRGCCA 沿一系列函数型积分投影方向将多元函数型数据投影至若干组数值变量;在整体相关性度量最大的准则下,借助函数型主成分分析(functional principal component analysis, FPCA)方法,确定主成分基函数展开系数,并最终估计最优积分投影方向。 经过大量数值验证,本文方法被验证能够快速有效探测多元函数型数据之间的相关关系,并得到相应最优投影权重函数的一致估计。 在实例研究中,通过帕金森综合征患者步态数据表明,由多元函数型数据投影得到的数值特征信息具有可解释性,本文方法具有一定实用价值。
1 FRGCCA 优化模型
考虑函数型随机变量{X(t):t∈F},F表示连续指标集。 对于任意t∈F,设X(t)均为数值随机变量,并存在二阶矩,即E[X2(t)] <∞,简记为X∈L2(F)。 这样,函数型数据的平方积分内积可以表示为

如式(1)所示,函数型数据X沿投影权重函数α被变换至一个数值积分投影。
对于J个函数型随机变量Xj∈L2(Fj)及其对应投影权重函数αj(j=1,2,…,J),FRGCCA 考虑极大化整体的相关性度量,即
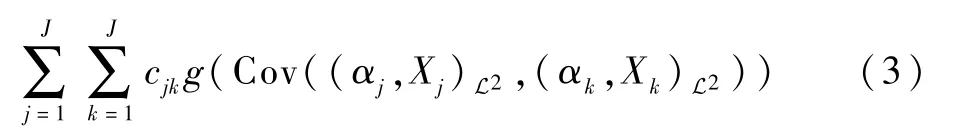
式中:连接参数cjk表示第j和第k个函数型随机变量之间是否存在关联性,当认为Xj与Xk相关时,cjk=1,否则为0;非负凸函数g(·)为给定的相关性度量;Cov(·,·)表示数值随机变量或随机向量之间的协方差或协方差矩阵。
与此同时,待估参数αj需要满足一定约束条件,即
式中:Var(·)为数值随机变量的方差;收缩参数τj∈[0,1]平衡投影方向长度和投影方差两方面约束,特别当τj=1 时,FRGCCA 具有多元PLS 的形式,当τj=0 时,FRGCCA 退化为广义典型相关分析。
2 FRGCCA 参数估计
本文重点讨论FRGCCA 的参数求解过程,即在式(4)约束条件下,使整体相关性度量式(3)达到最大的一系列最优投影权重函数的估计方法。
2.1 基函数展开
给定Fj上一组基函数ϕj= (ϕj1,ϕj2,…,ϕj,Sj)T,Sj为维数,对于任意t∈Fj,Xj可以表示为



2.2 最优投影权重函数估计
通过上述基函数展开表达,式(3)可以表示为

式中:Σjk= Cov(Uj,Uk);λj为拉格朗日乘子。
由L(aj,λj;j=1,2,…,J)关于aj的偏梯度可以得到平稳方程:

式(12)的推导过程详见附录A。

式(13)和式(14)优化过程基于一系列给定的基函数系统,即ϕj(j=1,2,…,J)。 事实上,ϕj的选取不会影响Fj上最优投影权重函数αj的最终结果(过程详见附录B)。
本文所提出FRGCCA 的求解算法总结如下:
步骤1 初始化。

如果ω≤ωmax,或者

注:本文采用基函数展开方法将函数型数据转换为一系列数值展开系数,通过对多组展开系数进行分析建模,以此重构得到对应函数型投影权重的相关结果。 这一建模思路表明:本文所提出的FRGCCA 方法同样适用于多组数值数据与一个或多个函数型数据同时存在的混合数据情形。 此时,数值变量和函数型变量分别在实向量空间和平方可积空间中通过各自投影实现数值化降维。 具体来说,在式(11)中,不妨假设第j个变量Xj退化为数值变量,此时选取实向量空间中的自然基ϕj,那么对应度量矩阵Wj退化为单位矩阵,aj即为Xj在ϕj下的投影权重向量。 相应计算过程与上述FRGCCA 求解算法保持一致。
2.3 其他因素
选取特定参数形式的基函数往往具有一定主观性[19];对此,本文采用基于数据驱动的FPCA方法确定基函数系统。 具体来说,在给定ϕj的基础上,FPCA 希望找到某个函数ξj∈L2(F),使得Xj与ξj的数值积分投影的方差最大:
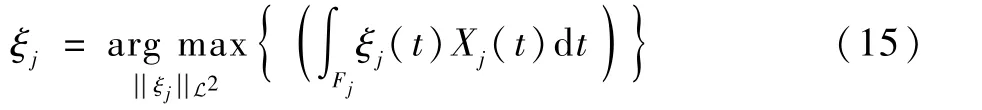
令vj表示ξj在ϕj下的展开系数,则式(15)等价于求解关于vj的多元主成分问题:


式中:0≤l0≤1 为设定的累积方差贡献率阈值。
通过标准正交基函数系统ξ0j= (ξ1j,ξ2j,…,

式中:mjkl(k,l=1,2,…,Sj)为Mj中第k行、第l列元素,mjkl和mjkk的方差用相应无偏估计替代。
3 数值实验
本节从3 个方面检验所提出FRGCCA 方法在有限样本情况下对多元函数型数据进行特征信息提取的表现,即函数型数据样本量、特征信息强度及观测扰动强度、收缩参数设置。
3.1 生成模型
考虑3 个定义在不同区间Ij上的函数型变量Xj(j=1,2,3),Xj由Ij上通过等间隔内节点决定的3 次B 样条基函数ϕj= (ϕj1,ϕj2,…,ϕj,Sj)T线性生成,生成系数为Uj。

对于非对角分块,
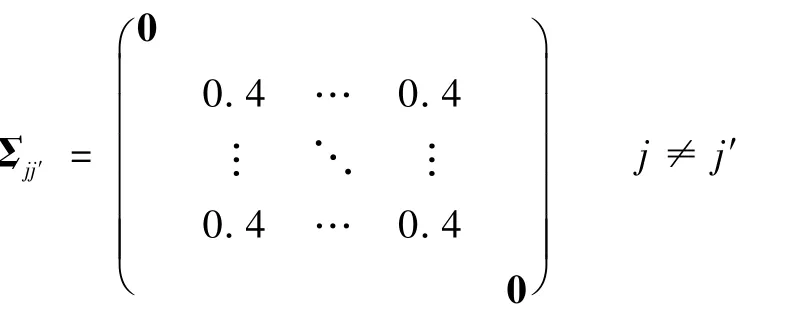
在3 组展开系数中,依次假设第2 至第3、第4 至第7、第8 至第11 个展开系数分量之间是相关的。 那么当τj=1 时,W1/2j aj的理论最优解为单位化向量(0,0,…,0,1,1,…,1,0,0,…,0)T,其中取值为1 的分量对应具有相关性的展开系数分量。 在上述假设下,首先从U中独立生成Xj的n组展开系数uij(i=1,2,…,n),然后在Ij上等概率选取T个时刻tj,并生成一系列数值观测:
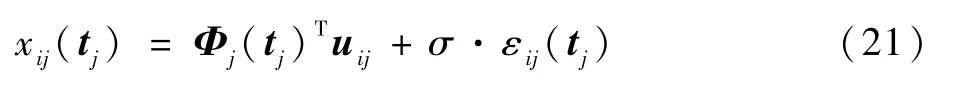
式中:Φj(tj)为如式(6)所示的数据矩阵;εij(tj)为从标准正态分布中独立产生的观测扰动;σ>0为控制扰动强度。
在每次实验中,假设3 个函数型变量之间两两相关,并使用Horst 型单位函数作为相关性度量;在FPCA 确定基函数系统过程中,选取通过相应区间上17 个等间隔内节点决定的3 次B 样条函数作为初始基函数。 记通过FRGCCA 估计得到的最优投影权重函数及其对应展开系数分别为^αj和^aj,用积分平方误差(integral square error,ISE)衡量^αj的估计精度,即
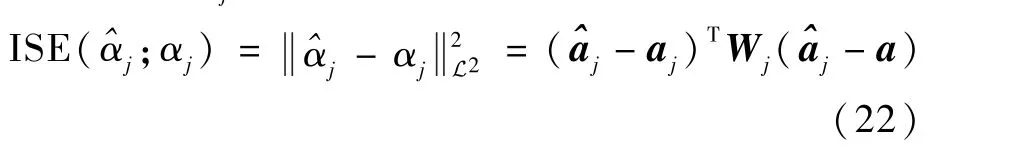
对于式(21)生成模型中的每种参数设置,独立重复进行1 000 次数值实验。
3.2 函数型数据样本量
考虑不同函数型数据样本量n对^αj的影响。在式(21)生成模型中,依次从n=200 增加至n=1 000,并固定T=200、σ=0.1 及收缩参数τj=1(j=1,2,3)。 表1 报告了不同函数型数据样本量情况下,^αj关于αj理论最优解的ISE(放大100 倍)的均值和标准差。
从表1 中可以看到,随着n的增加,^αj的均值与相应理论最优解的差距一致减小,其标准差也同步减小;基于FPCA 生成基函数得到的估计结果,逐步趋近于已知真实设定基函数系统及投影权重函数展开系数的理想情况。 上述数值结果表明,所提出FRGCCA 方法能够在有限样本情况下对αj的估计具有一致性。
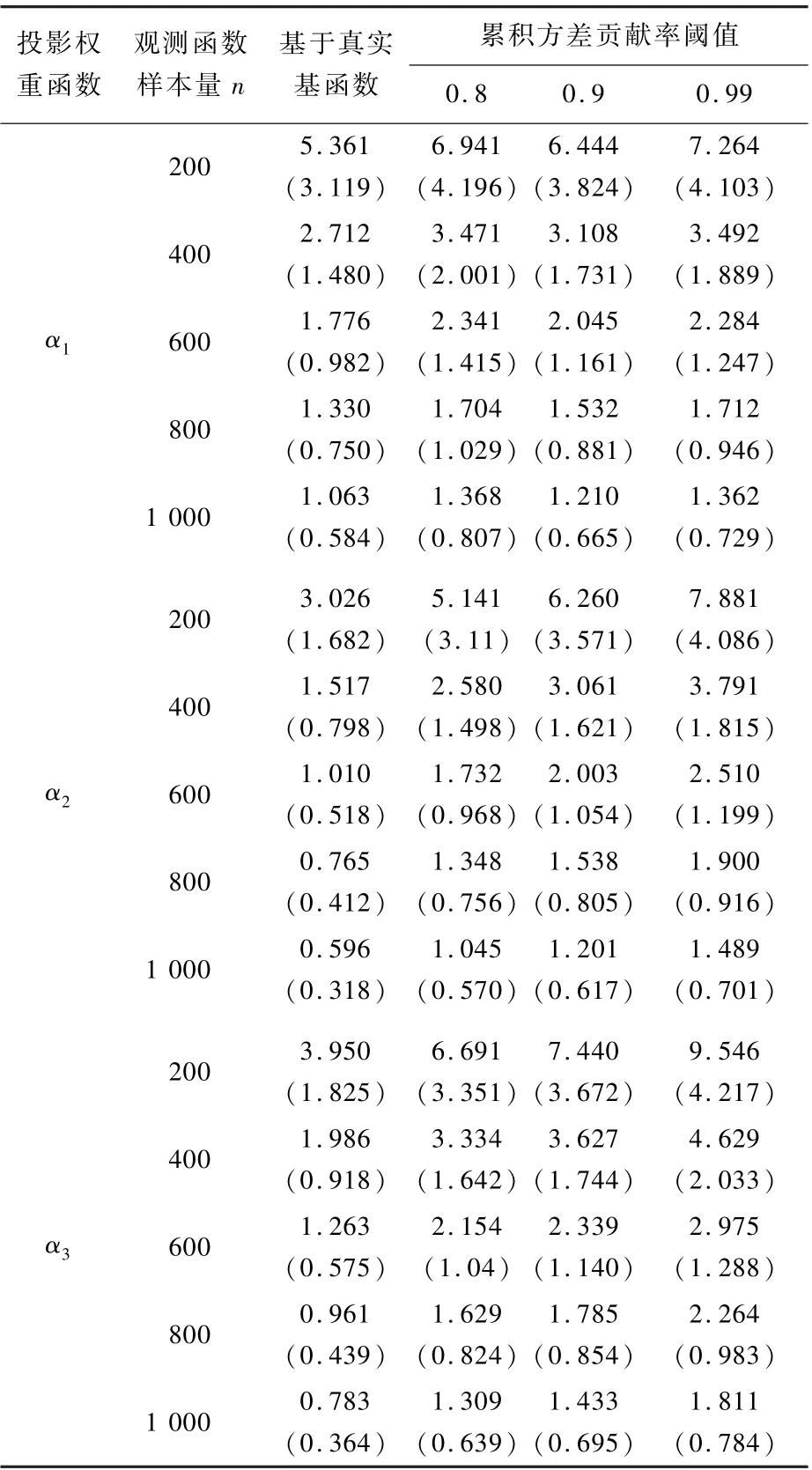
表1 不同函数型数据样本量下FRGCCA 的估计精度Table 1 Estimation accuracy of FRGCCA under different sample sizes of functional data
3.3 特征信息及扰动强度
用函数型数据中数值观测量T的大小来衡量相应特征信息强度,考虑T对^αj的影响。 在式(21)生成模型中,依次设T=50,100,…,300,并固定n=500、σ=0.1 及τj=1(j=1,2,3)。 表2 报告了不同数值观测量情况下,关于αj理论最优解的ISE(放大100 倍)的均值和标准差。
从表2 中可以看到,当函数型数据中数值观测量较少(如T=50)时,对αj的估计也普遍较差;当观测量适量增加时,相应估计结果将显著提升,并同样接近真实设定基函数系统及投影权重函数展开系数已知情况下的理想结果。 然而,在达到一定规模(如T=200)后,由于基函数展开存在截断误差,过多的数值观测无法进一步提高估计精度。
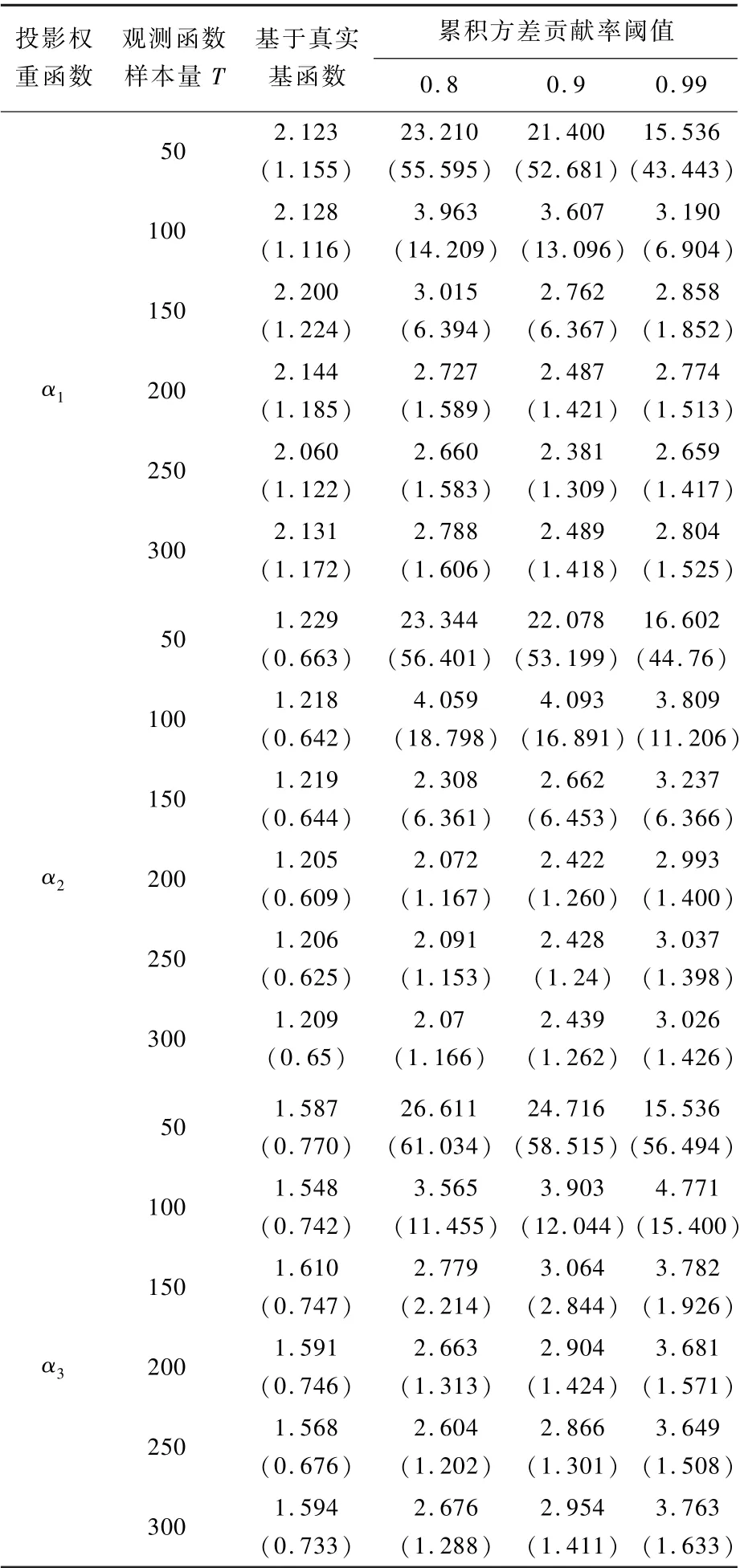
表2 不同数值观测量下FRGCCA 的估计精度Table 2 Estimation accuracy of FRGCCA under different sizes of observations
在本节参数设置基础上,固定T=200,并考虑不同扰动强度σ∈{0,0.2,…,1}。 特别地,σ=0 表示生成模型中不存在观测扰动,但由于使用FPCA 确定基函数系统,相应展开系数并不等同于由分布生成的真实设置。 表3 报告了不同数值观测扰动强度情况下,^αj关于αj理论最优解的ISE(放大100 倍)的均值和标准差。 从表3 中可以看到,增加σ虽然从整体上增加了^αj的偏差,但增加程度相对较小。
由表1 ~表3 可知,在FPCA 确定基函数系统过程中,设定较小的累积方差贡献率阈值(如l0=0.8)即可得到较好的估计结果;设定过大的累积方差贡献率阈值(如l0=0.99)将引入不必要的观测扰动信息,从而干扰优化过程,使得估计结果产生一定偏差和波动。 此外,累积方差贡献率阈值的经验设定可以根据函数型数据的数值观测量进行调整。 当数值观测不足时,需要通过较多的基函数展开系数尽可能挖掘函数型数据的变化特征,即设置较大的l0;而当观数值观测较多时,则需要适当减少使用的展开系数个数,以避免过拟合。 不过,累积方差贡献率阈值的设定并不会对投影权重函数的估计产生显著影响。
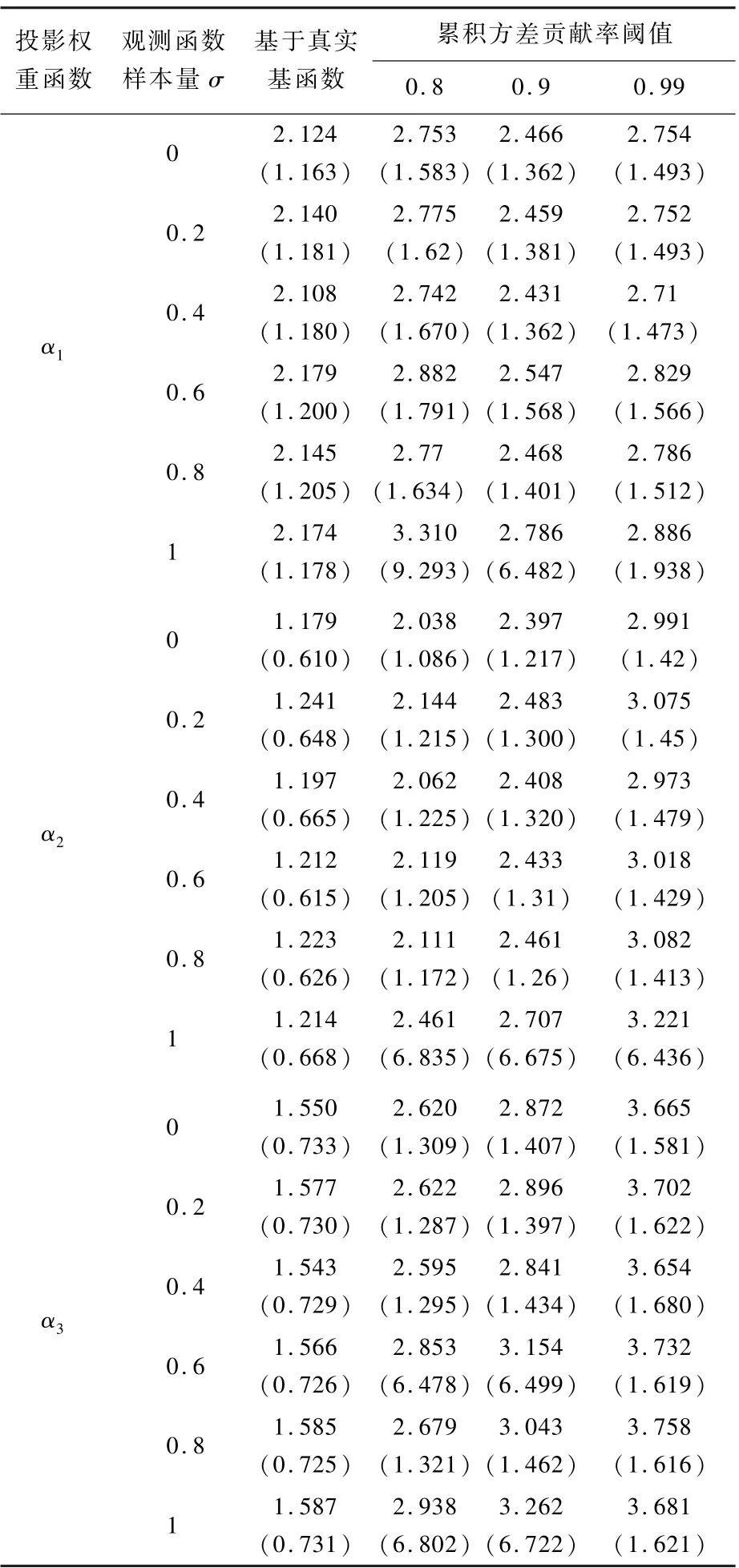
表3 不同数值观测扰动强度下FRGCCA 的估计精度Table 3 Estimation accuracy of FRGCCA under different perturbations of observations
3.4 收缩参数
考虑不同收缩参数τj对^αj的影响。 在式(21)生成模型中,设n=600、T=200 且σ=0.1。 为了衡量^αj的整体波动,考虑^αj在Ij上的积分方差(integral variance, IVar),即
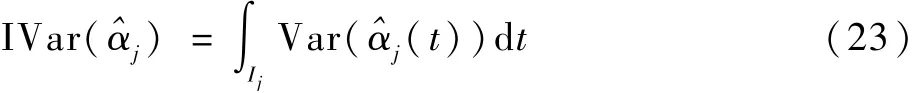
图1 展示了收缩参数从1 同步变化至0 情况下,相应IVar(^αj)的折线图。 图中:竖直线段表示均值加减一个标准差范围。 此外,设l0=0.9。
如图1 所示,随着τj减小,IVar(^αj)的均值和标准差显著增加,这意味着^αj逐渐偏离τj=1 时αj的理论最优解,并具有更大波动。 事实上,在式(4)约束条件中,τj=1 要求αj具有单位函数长度,这使得αj无法变化很大;当τj逐渐减小时,这种约束随之减小,αj的变化程度则相应增加。图1验证了τj在FRGCCA 中的正则化功能,这与传统RGCCA 框架中的有关结论是一致的。
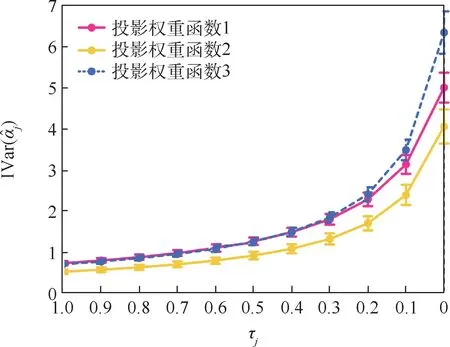
图1 不同收缩参数下FRGCCA 估计结果的Ivar 折线图Fig.1 Line chart for IVar of FRGCCA under different shrinkage parameters
4 实例分析
本节通过有关帕金森综合征患者行走步态的实例数据(简称Gait 数据集)检验所提出FRGCCA 方法的实用性。 表4 简要介绍了本文使用的Gait 数据集中4 组指标变量,更加详细的描述参见Goldberger 等[21]的研究。
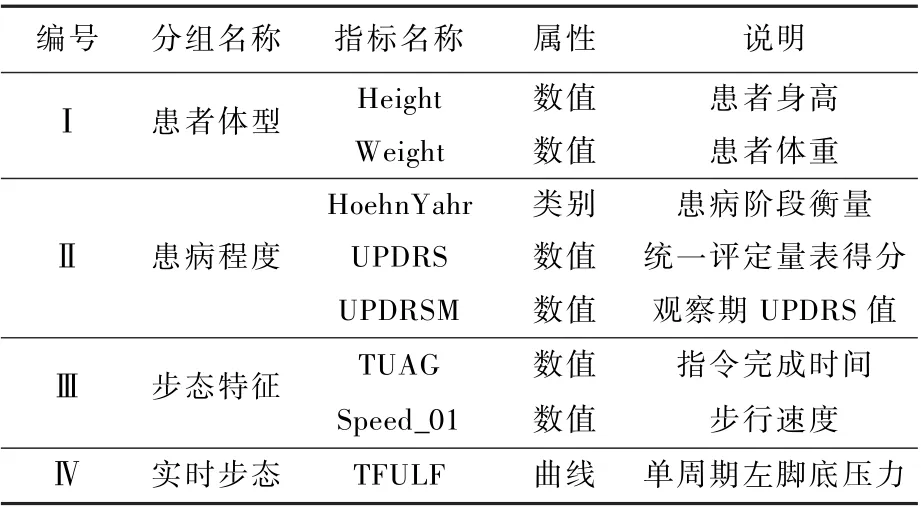
表4 Gait 数据集指标变量说明Table 4 Gait dataset indicator variables description
值得说明的是,在Gait 数据集中,同时存在若干组数值变量(患者体型等)和一个函数型变量(实时步态)。 按照本文所提出FRGCCA 方法采用的基函数展开思路,函数型数据和传统数值数据混合的情形同样适用于本文方法。 本文只需将函数型变量转化为对应的基函数展开系数。
首先将高频采集的TFULF 原始数据曲线进行分割,通过核函数估计方法对一系列分割的原始曲线进行拟合,并对齐至0 ~1 的区间,其中0和1 分别表示一步行走的开始和结束。 图2 展示了编号为“GaPt28”和“SiPt08”患者的TFULF 原始数据和拟合曲线。
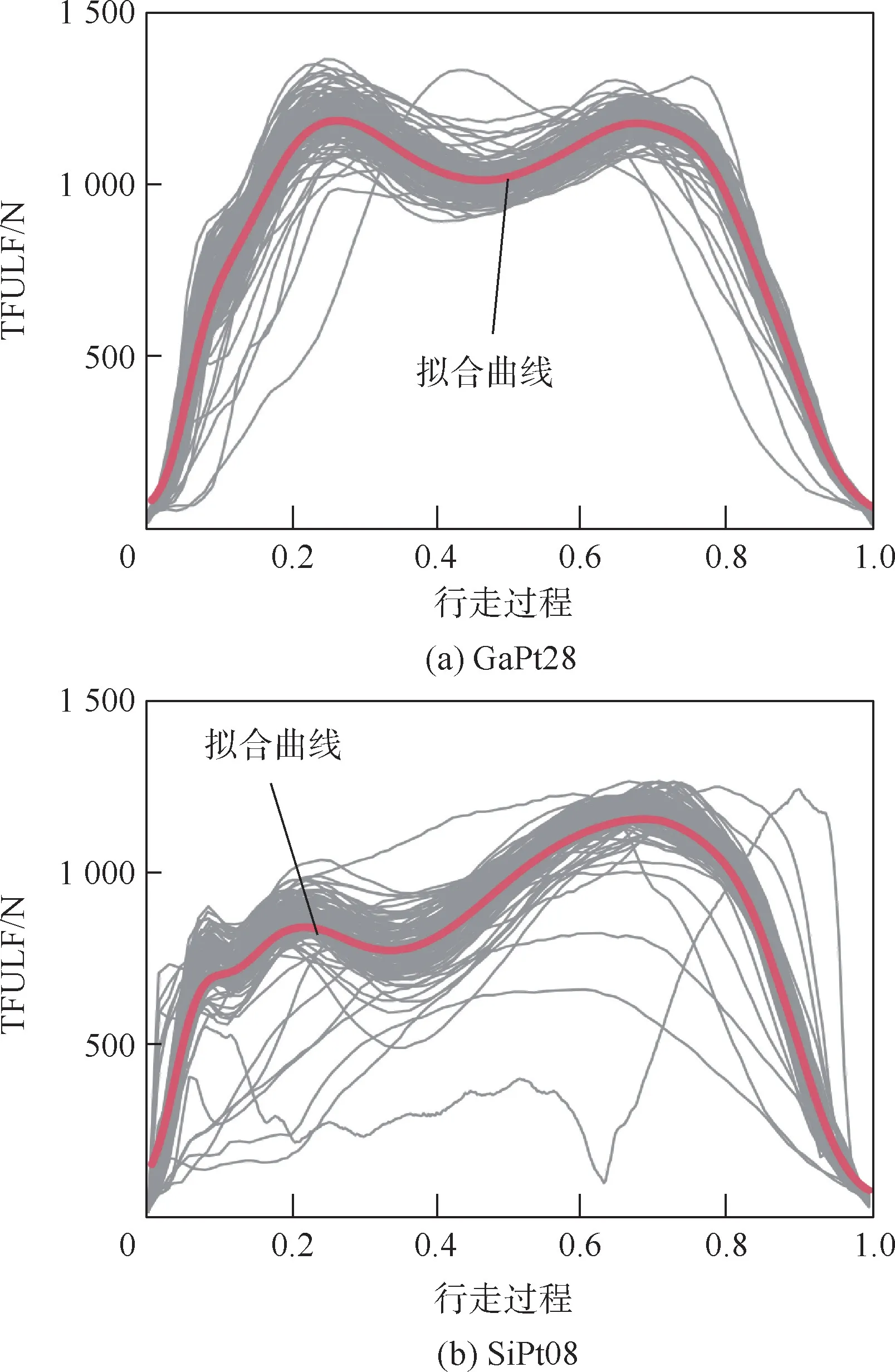
图2 Gait 数据集TFULF 曲线示意图Fig.2 Diagrams of curves of TFULF for Gait dataset
然后对上述指标变量建立FRGCCA 模型。采用Horst 型单位函数作为相关性度量,令收缩参数均为1,并假设“患者体型”与“患病程度”2组指标变量之间不存在相关性,那么相应关联关系矩阵为

在FPCA 确定基函数系统过程中,将通过[0,1]中17 个等间隔内节点决定的3 次B 样条函数作为初始基函数,并设l0=0.95。 与此同时,通过重抽样算法构造投影权重函数估计的置信域,并进行1 000 次独立重复实验。 在每次重复实验中,有放回选取80%实验数据。 表5 报告了通过全样本估计得到的3 组多元数值变量的最优投影方向估计及其相应经验置信区间。 图3 展示了函数型变量TFULF 对应最优投影权重函数的全样本估计及5%置信水平下的经验置信带。
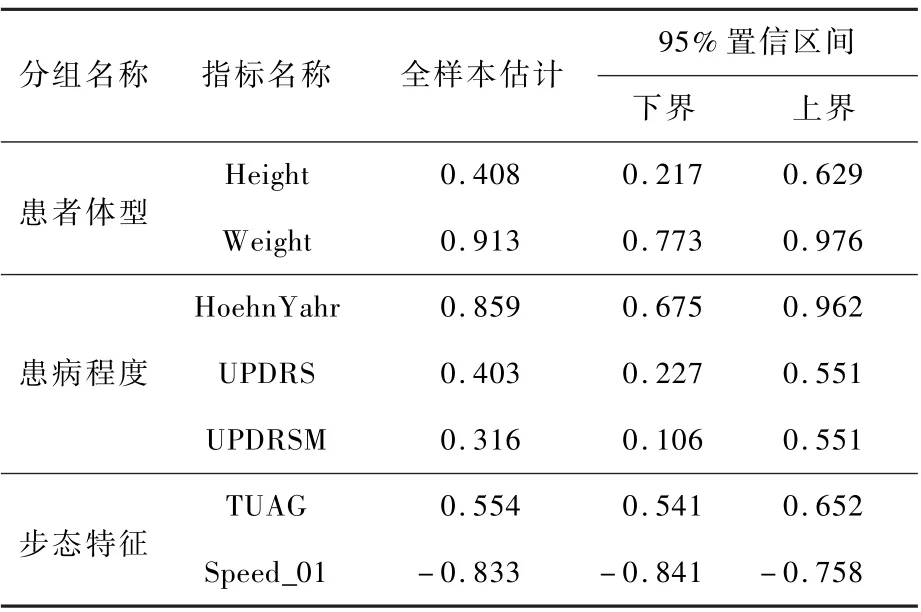
表5 三组多元数值变量对应投影权重向量的估计结果Table 5 Estimated results of corresponding weighted integral vectors for three multivariate groups
从表5 中可以看到,在“患病程度”分组中,投影权重向量的分量均为正数,这说明通过投影得到的数值特征信息与帕金森综合征患者的患病程度呈正相关关系。 与此同时,“步态特征”分组对应投影权重向量也印证了这一事实,即患病越严重,患者行走速度越慢、完成一个步态周期所需的时间也就越长。 在此基础上,“患者体型”分组对应估计结果说明,对于帕金森综合征患者而言,身高越高或体重越大均会加重患病的严重程度,且体重对于患病程度的影响更大。 在经验置信区间方面,FRGCCA 得到估计结果的置信区间普遍较窄,且在5%置信水平下均显著不为零。
从图3 中可以看到,TFULF 对应的最优投影权重函数估计曲线在步态周期开始(完成20%前)和结束(完成80%左右)存在2 个显著高于零的波峰,这一结果说明起步和收尾阶段的步态情况对判断帕金森综合征患者的患病程度存在显著关联。
5 结 论
本文提出对于多元函数型数据的RGCCA 理论,即FRGCCA,并推导其迭代求解算法。
1) 本文所提出FRGCCA 方法将RGCCA 的理论框架推广至FDA 领域,实现了对多元函数型数据特征信息的数值化提取及快速降维。
2) 通过基函数展开方法,推导得到关于最优函数型投影权重方向的迭代估计方法,该方法对于基函数系统的选取具有独立性。 通过基于数据驱动的FPCA 方法确定标准正交的基函数系统。
3) 通过一系列数值实验,从3 个方面说明了所提出FRGCCA 方法在有限样本情况下对投影权重函数的估计具有一致性,并有效实现多元函数型数据特征信息的数值化提取及快速降维。
4) 在对于Gait 数据集的实例数据研究中,所提出FRGCCA 方法得到的数值特征信息与患病程度呈正相关关系,由此验证了所提出方法的实用价值。
附录A:
附录B:
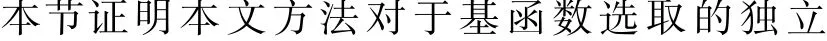

此时由式(B2)可以验证

