基于特征根有界摄动分析的高超声速飞行器双通道控制

杨雨宸 张增辉 闫佳宁 张晶 杨凌宇

(1. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083; 2. 北京机电工程总体设计部, 北京 100854)

高超声速飞行器飞行状态变化剧烈,包线范围跨度极大,是近年来各国争相发展的前沿技术[1-2]。 在多种气动控制方案中,以HTV-2 为代表的高超声速飞行器采用了一种双通道控制方案[3],其仅用一对升降副翼完成了飞行器的姿态控制,优点是可以有效降低飞行器结构复杂度、减轻质量;但对飞行器本身的气动特性和控制方法提出了更高的要求,尤其对于具有强不确定性的高超声速飞行器,该问题更为复杂。

与传统飞控系统设计不同,高超声速飞行器的高马赫飞行速度使得其对各类参数变化非常敏感,也由此带来了强不确定性、强耦合等问题,给其控制系统的设计带来了巨大挑战。 近年来,学者们进行了大量关于高超声速飞行器姿态控制的研究,包括自适应、鲁棒H∞、滑模、容错和智能等多种控制方法也都被运用在了其控制系统设计上[4-7]。 而对于类HTV-2 气动布局飞行器的双通道控制问题,相关研究相对较少且主要集中在理论研究层面。 文献[8]研究了非最小相位欠驱动高超声速飞行器的二阶动态滑模控制问题,通过系统分解的方法设计了滑模控制器。文献[9]从工程应用的角度出发,针对气动控制舵面仅有体襟翼的情况提出了一种基于欠驱动构型飞行器耦合特性的横侧向控制策略。 文献[10]针对只有2 个舵的欠驱动再入飞行器,分别针对快回路和慢回路设计了超扭曲滑模控制器和分层滑模控制器,组成了具有抗饱和功能的姿态跟踪控制器。 文献[11]提出了基于输出重定义的非最小相位动态逆控制方法,利用根轨迹法确定控制输出组合系数,实现系统零动态的分配。

可以看出,先进控制方法在稳定性理论和仿真验证方面取得了重要的进展,但仍未在工程设计界广泛应用,如何将先进控制理论与工程需求相结合仍是一个重要的问题。

在飞行器控制工程设计中,基于极点和模态的概念仍然是工程上分析和设计的重要手段,将欠驱动问题与模态设计结合起来,并提供适用的鲁棒性分析方法,对改善现有飞行控制设计流程和推进现代控制理论的工程化有较强的研究意义。

针对上述问题,本文以双通道高超声速飞行器为对象,以系统的闭环极点为结合点,提出基于特征根有界摄动分析的鲁棒性评价手段,并以六自由度非线性对象为例进行了对比分析和验证。首先,建立了NASA Winged-Cone 飞行器六自由度非线性模型;然后,给出了荷兰滚模态与气动系数之间的近似关系,并提出了2 种可行的双通道控制方案;同时,提出了特征根灵敏度矩阵与特征根有界摄动系数的概念及鲁棒性分析方法;最后,基于非线性模型进行了对比分析与验证。

1 高超声速飞行器非线性建模

本文所建立的高超声速飞行器再入模型采用NASA 兰利研究中心提供的公开高超声速飞行器Winged-Cone 的气动数据及总体参数[12],其气动布局如图1 所示。

图1 Winged-Cone 气动布局[12]Fig.1 Winged-Cone pneumatic layout[12]

Winged-Cone 采用三角机翼布局,尾部有左右独立工作的升降副翼和带有方向舵的垂直尾翼,前端还有可收缩的水平鸭翼。

在飞机的舵面使用上,由于本文主要针对无动力滑翔阶段,水平鸭翼收入机体不参与控制;另外,为开展双通道控制研究,将方向舵始终固定于平衡位置,飞机仅采用左右升降副翼完成姿态控制。

建模中所用到的其他假设如下:

1) 飞行器为理想刚体。

2) 无动力滑翔过程中质量不变,且推进系统不工作,即推力为0。

3) 飞行器为面对称,故近似认为惯性积Ixy和Iyz为0。

4) 地球为平面大地。

基于上述假设给出被控对象质心运动学模型为[13]

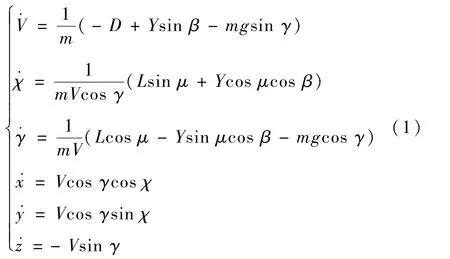
式中:[Vχγxyz]T分别为速度、航迹方位角、航迹倾角,以及质心在地球坐标系下的三轴位移分量;L、D、Y分别为升力、阻力、侧力;m为飞行器质量;g为当地重力加速度。

姿态动力学模型为

式中:[αβμpqr]T分别为迎角、侧滑角、倾侧角、滚转角速率、俯仰角速率和偏航角速率;Ix、Iy、Iz为转动惯量;Ixz为惯性积;LA、MA、NA分别为飞行器总的滚转力矩、俯仰力矩、偏航力矩。

非线性的气动力和气动力矩计算分别如下:

式中:CX、CY和CZ为气流系三轴力系数;Cl、Cm和Cn为三轴力矩系数,具体数值详见文献[12];Q为动压;S为机翼参考面积;b为翼展;c为气动弦长;Xcg为重心与取矩中心距离。

各参数具体数值如表1 所示。

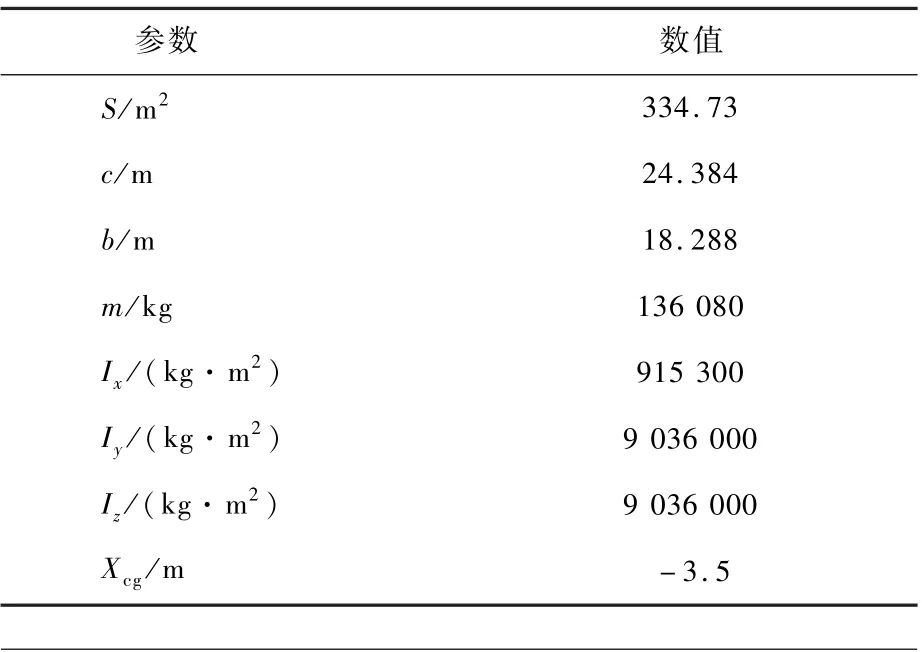
表1 Winged-Cone 主要参数Table 1 Key parameters of Winged-Cone

方程(1) ～(4)共同组成了所用的高超声速飞行器再入段的六自由度非线性模型。

2 荷兰滚模态分析及反馈控制方案

双通道控制的一个重要问题在于飞机的横侧向处于欠驱动状态,无法独立完成横向和航向的解耦控制,因此,如何利用单个控制量抑制荷兰滚模态的影响,并完成对横滚运动的跟踪控制,成为双通道控制的一个重要问题。

本节先从Jacobi 线性化得到的横侧向运动模型出发,推导荷兰滚模态的极点与气动参数关系;再结合工程要求,确定合理的反馈量与反馈形式,进而给出改善横侧向闭环特性的可行方案。

2.1 横侧向模态特性分析

选取横侧向状态对模型进行Jacobi 线性化,可以得到如下线性模型:

其中:Y′*、N′*和L′*分别为侧力、偏航力矩、滚转力矩对下角标变量的偏导数;γ0和α0分别为当前配平工作点的航迹倾角和迎角;δa为等效副翼。

矩阵AL中各元素为

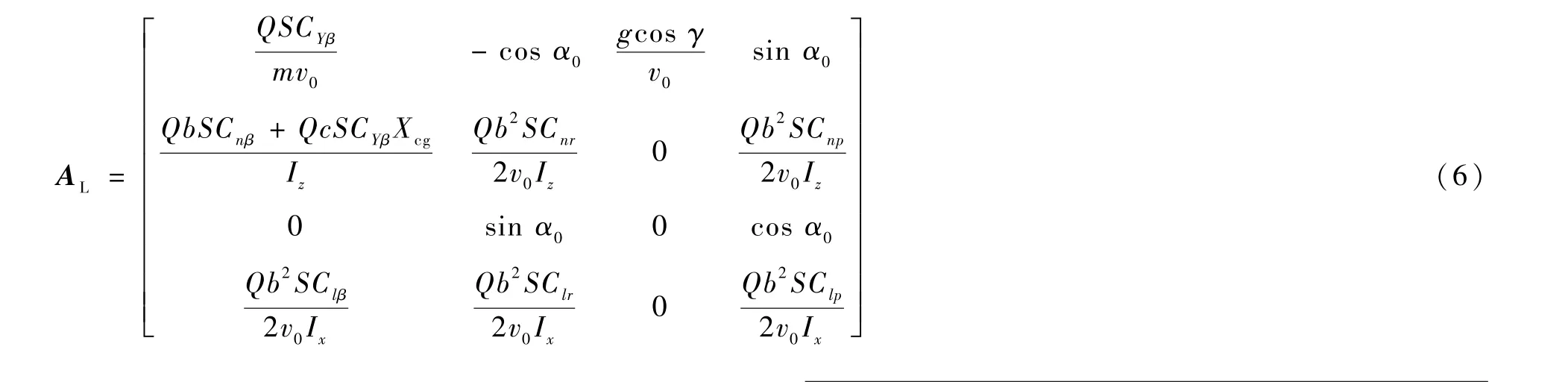
式中:v0、α0分别为线性化工作点处的空速、迎角;Cnβ为偏航力矩系数关于侧滑角偏导数;CYβ为侧力关于侧滑角偏导数;Clβ为滚转力矩系数对侧滑角偏导数;Cnr、Clp分别为偏航、滚转力矩系数的偏导数;Cnp、Clr为交叉力矩系数的偏导数。

对于面对称飞行器,矩阵AL特征方程一般为

式中:ξ和ω分别为荷兰滚模态阻尼比和固有频率; -λr为滚转阻尼模态极点; -λs为对应螺旋模态极点;In为n×n单位矩阵。

考虑到高超声速飞行器在整个飞行包线内气动特性变化显著,因此,选取滑翔段设计包线为α∈[ -2°,14°],马赫数Ma∈[4,12],对模型的横侧向特性进行分析,结果如图2 ～图4 所示。

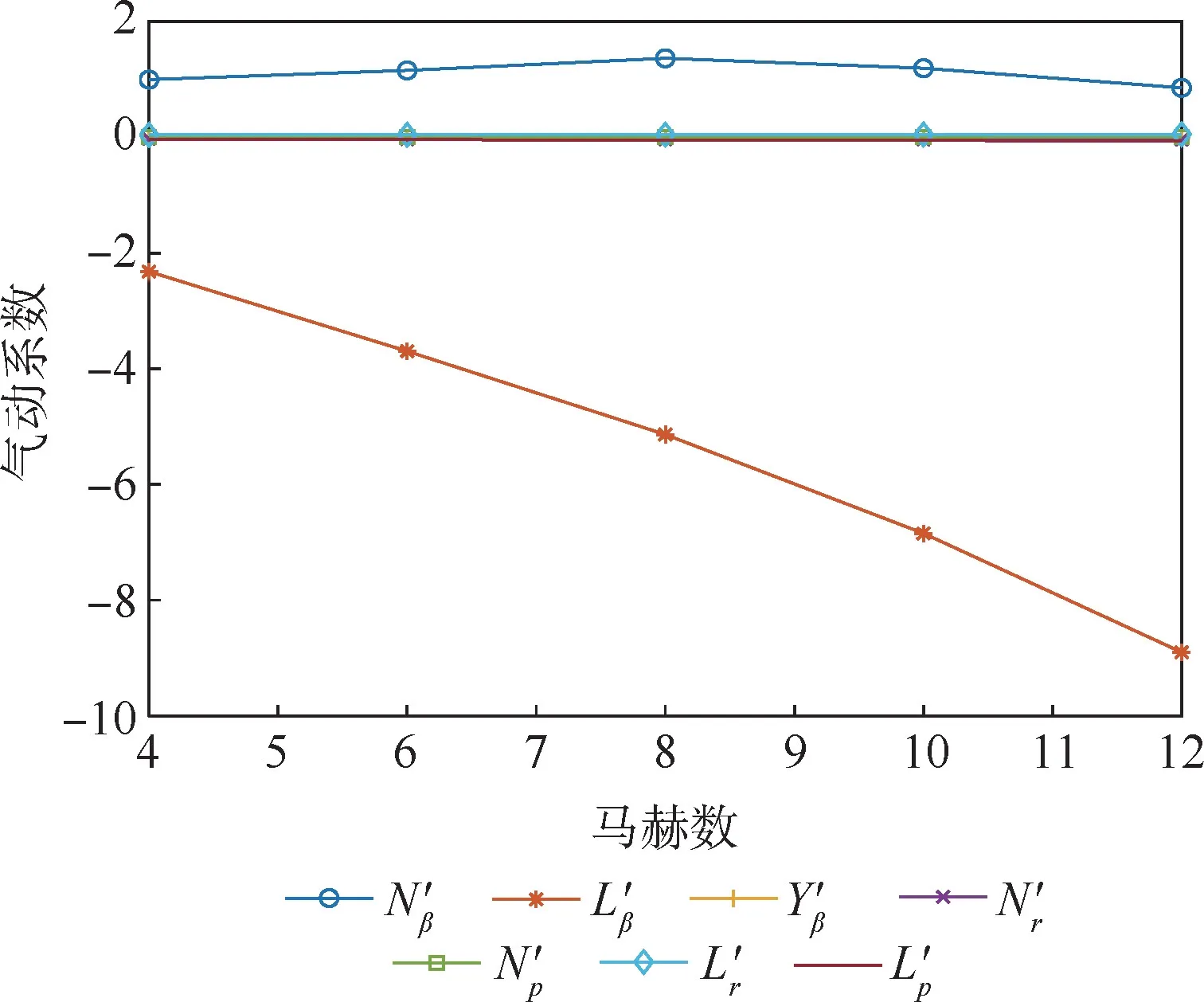
图4 气动系数随马赫数变化曲线Fig.4 Aerodynamic coefficients with Mach number

图2 为迎角12°时螺旋模态和滚转阻尼模态极点随Ma变化的曲线。 可以看出,Winged-Cone飞机与传统飞机类似,其螺旋模态对应非常小的实根,滚转阻尼模态对应较大的负实根,极点值在[ -0.03, -0.035]之间,大约为螺旋模态极点模值的5 ～10 倍。

图2 螺旋与滚转阻尼模态极点Fig.2 Spiral mode and roll-damping mode poles

图3 为荷兰滚阻尼比随迎角与马赫数变化曲线。 可以看出,在整个包线内荷兰滚模态阻尼很小,约在[0.005,0.025]之间,必须采用控制方法加以改善。

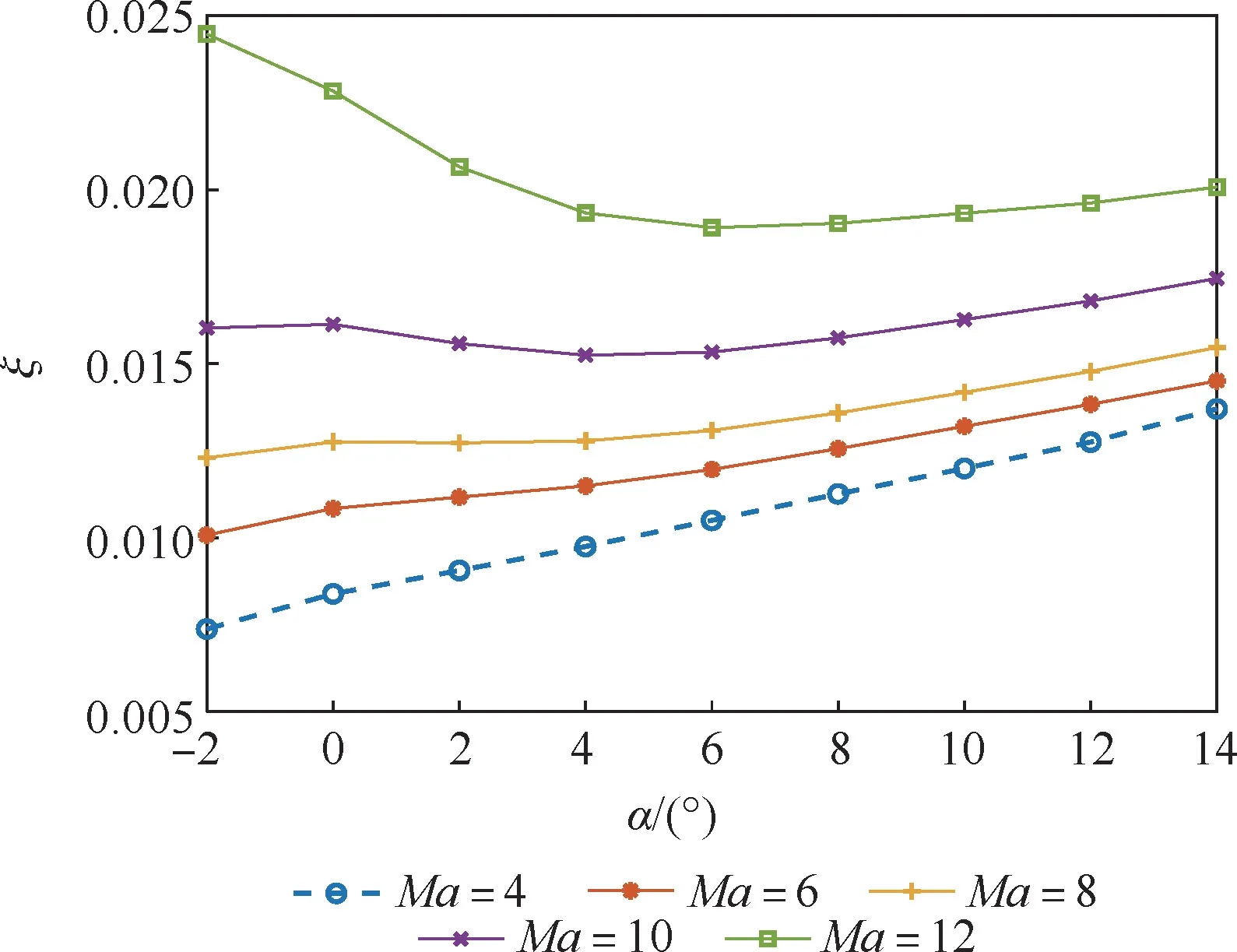
图3 荷兰滚阻尼比随迎角和马赫数变化曲线Fig.3 Dutch roll damping ratio with angle of attack and Mach number

另外,为了分析矩阵AL中各元素对闭环特性的影响,给出了矩阵AL主要气动参数随马赫数变化的曲线,如图4 所示。 可以看出,在所有气动系数中,N′β与L′β比其他元素大1 ～2 个数量级。

根据上述分析,可以发现此类飞行器具有以下特点:

1) 滚转阻尼模态极点数值远远大于螺旋模态极点,即λs≪λr。

2) 荷兰滚阻尼比ξ≪1,需要改善。

3)N′β与L′β比其他气动参数大1 ～2 个数量级。4) 副翼对航向控制效率近似为0,即N′δa≅0。

2.2 荷兰滚模态近似特性计算方法

传统飞行控制中对荷兰滚模态的近似分析方法基于克莱姆法则,在简化过程中忽略了交叉倒数项,如L′β、N′p等[14],对包含方向舵的飞行器可得到简单可行的控制方案;但对双通道控制飞机,由于缺乏方向舵改善荷兰滚阻尼,必须找到通过副翼改善荷兰滚阻尼的手段,本节采用多项式分解的方式,对多项式的每一系数分别讨论。

横侧向特征方程(7)可展开表示为

相对计算误差定义如式(21)所示。 为了验证式(21)的准确性,引入文献[14]中的传统方法进行对比,对设计包线内的荷兰滚模态的ξ和ω进行了计算,比较结果如图5 和图6 所示。

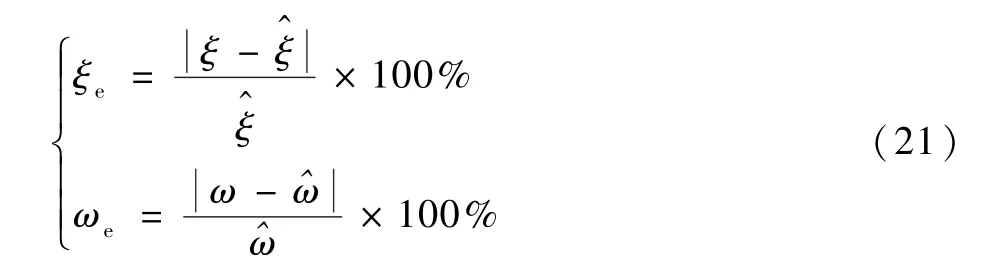
图5 飞行包线内ξ 相对估计误差Fig.5 Relative estimation error of ξ in flight envelope

图6 飞行包线内ω 相对估计误差Fig.6 Relative estimation error of ω in flight envelope

式中:ξ^ 和^ω分别为ξ和ω的真值。

图5 和图6 中,红线为各马赫数下本文方法得到的相对误差,蓝线为传统方法计算得到的相对误差[14]。 从图中误差结果来看,在整个设计包线内,所推导的荷兰滚阻尼比相对误差都在21%以下,固有频率相对误差小于1%,估计精度明显优于文献[14]中的荷兰滚预测方法,这表明推导的荷兰滚模态关系足以满足研究的需要。

2.3 横侧向反馈控制方案分析

双通道控制的难点在于缺少产生航向力矩的舵面,因此其荷兰滚模态的改善不能采用常规方式。 本节根据荷兰滚模态与气动系数之间的关系来研究可行的反馈控制方案。

由式(20),并注意Y′β、N′r和L′β均为负,可得出以下结论:

1) 减小Y′β、N′r和N′β均能改善荷兰滚阻尼,这也是常规飞行器改善荷兰滚特性的主要手段,但对于双通道控制飞行器,其副翼对偏航和侧力的操纵效率极低,需要较大增益才能对这3 项产生明显影响,考虑到舵偏限制,该方式在工程上不具备可行性。

2) 观察式(20)实部中L′p相关项,当α0很小时,2 项近似相消,因此增大L′p对荷兰滚模态的改善效率很低,但增大L′p对改善滚转阻尼模态具有较强的效益[14]。

3) 增大L′β绝对值能改善荷兰滚阻尼,且由于副翼对滚转操纵效率较高,不存在舵偏过限的问题,因此工程上是可以实现的。

综合上述结论,较为合理的反馈状态量选取应为侧滑角与滚转角速率,给出“极点配置方案”,该方案的主要思路为:通过合适的增益反馈改变L′β与L′p的值,进而改善闭环系统和荷兰滚特性。 按照前述反馈策略,配置反馈增益:

除了上述“极点配置方案”,工程上经常采用一种通道隔离的解耦设计方法,即将被控状态与动态性能差的状态解耦,以降低影响。 对于滑翔段,其主要控制量为航迹倾角,若将其与荷兰滚模态解耦,也可以达到设计要求,因此本文提出了“解耦控制方案”,其基本思想为:偏航通道利用对象本身静稳定性实现镇定,不再追求荷兰滚模态快速收敛;反馈目的变为消除偏航通道对滚转通道的影响,也就是通过反馈来降低L′β;对滚转通道实现合理增稳。

解耦控制方案的控制结构与极点配置方案相同,但K的设计过程需要满足:

3 特征根有界摄动分析方法

对于高超声速飞行器,其强不确定性会直接影响系统闭环极点,进而导致系统动态性能偏离预期,定量分析闭环极点随系统参数变化的程度和趋势对评价系统鲁棒性具有较强的指导意义。

在对一般矩阵特征根求导理论[15]基础上,本节提出一种特征根有界摄动分析方法,通过求取闭环系统的横侧向模态极点关于各参数的灵敏度,来定量分析闭环系统对参数摄动的鲁棒性,以判定工程实际中控制方法可行性。

定义1 设系统矩阵A∈Rn×n有n个互异特征根λk(k=1,2,…,n),则称Λk= ∂λk/∂A为第k个特征根λk所对应的特征根灵敏度矩阵,表示为

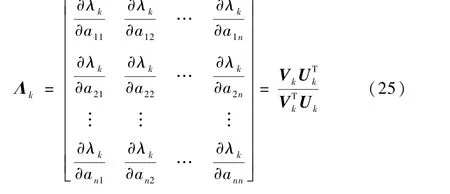
式中:aij为A中第i行j列的元素;Vk和Uk分别为λk所对应的右特征向量和左特征向量。

可见,特征根灵敏度矩阵表示的是矩阵中某元素对给定特征根的影响程度,该值越大,说明系统特征根对该参数越敏感。

式(25)推导过程如下:首先,根据特征向量定义,Vk和Uk分别满足:

特征根灵敏度矩阵Λk体现了系统对各参数单位变化时的敏感程度,但其并不与各参数的摄动程度直接关联,为了定量体现不确定性对特征根的影响,本文提出了特征根有界摄动矩阵的概念。

定义2 设系统阵为A∈Rn×n的参数摄动量化矩阵为R,满足:

特征根有界摄动系数为

定义2 引入了参数摄动修正项R,可以看出Γk中的每一个元素代表对应参数在摄动范围内对极点的最大影响,而ηk则表征所有参数最大影响的叠加,ηk越大,说明系统特征根的鲁棒性越差,反之则鲁棒性越好。

通过引入上述概念,考虑了工程应用中的实际参数摄动情况,进一步提升了其适用性,也能更准确地帮助判断所设计的闭环系统对于参数摄动的鲁棒性。

基于前述分析与方法,下文将结合对象模型在具体工作点给出2 种不同的控制方案,并用所提特征根有界摄动矩阵来判定2 种控制方案的鲁棒性。

4 仿真结果与分析

为验证本文方法,选取工作点为马赫数10、高度36 km、迎角4°为例进行2 种方案的设计与分析。 首先,给出此工作点的线性化模型为

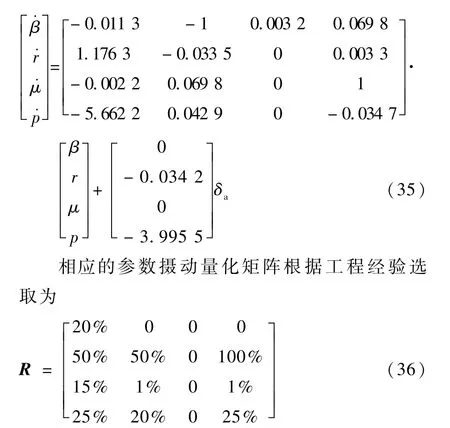
设舵偏限幅为±35°,舵机模型选择为

可知,原系统荷兰滚模态与滚转阻尼特性都需要改善。

基于上述设定,基于六自由度非线性模型作为被控对象,本节将对所提出的2 种控制器设计方案及特征根有界摄动矩阵的计算过程进行比较和分析。

4.1 极点配置反馈控制方案

经2.3 节分析,已经确定为侧滑角与滚转角速率,那么主要问题在于确定反馈增益。 设期望荷兰滚阻尼比和滚转阻尼极点要求为

从系统极点来看,经过对侧滑角的大增益反馈,显著提升了荷兰滚阻尼,并且加大了滚转阻尼,标称状态下满足预期设计要求。 采用特征根有界摄动分析方法判断方案1 的鲁棒性,按式(33)分别求λd1、λr所对应的特征根有界摄动矩阵分别为

特征根有界摄动系数分别为

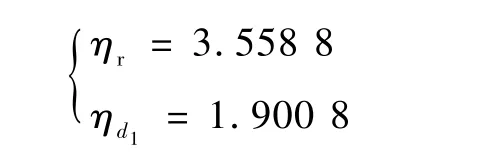
从特征根有界摄动矩阵来看,闭环系统极点在R所描述的摄动情况下,对L′p、N′p、L′β项的摄动比较敏感,在实际复杂环境下飞行时,可能会严重影响闭环极点,进而导致该控制方案鲁棒性较差。

为了验证上述结论的正确性,参照参数摄动量化矩阵(36)对L′p项加入±25%的参数摄动,即在区间[ -9.033 4, -5.420 0]变化,绘制闭环系统极点随L′p变化的情况,如图7 所示,其中线条越粗大代表L′p越大。

从图7 中可以看出,荷兰滚模态在加入参数扰动后依旧在左半平面变化,但滚转阻尼极点变化非常剧烈,在有限的参数摄动下甚至会导致系统的主导极点改变,严重影响闭环系统性能。 这样的结果与上文计算的Γr、Γd1保持了一致。

图7 方案1 极点受L′p扰动的影响Fig.7 Poles of method 1 vary with L′p

为了进一步说明本文方法的有效性,进行了闭环六自由度非线性仿真,分别为标称状态和拉偏状态仿真,参数拉偏包含气动系数误差、大气密度误差、总体参数误差及风干扰,均取工程极端偏差值,总扰动与式(36)相匹配。 倾侧角跟踪曲线及侧滑角和舵偏的响应曲线如图8 ～图10 所示。

图8 方案1 倾侧角响应Fig.8 Bank angle response of method 1

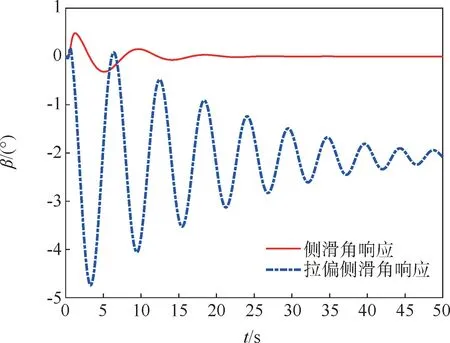
图9 方案1 侧滑角响应Fig.9 Sideslip angle response of method 1

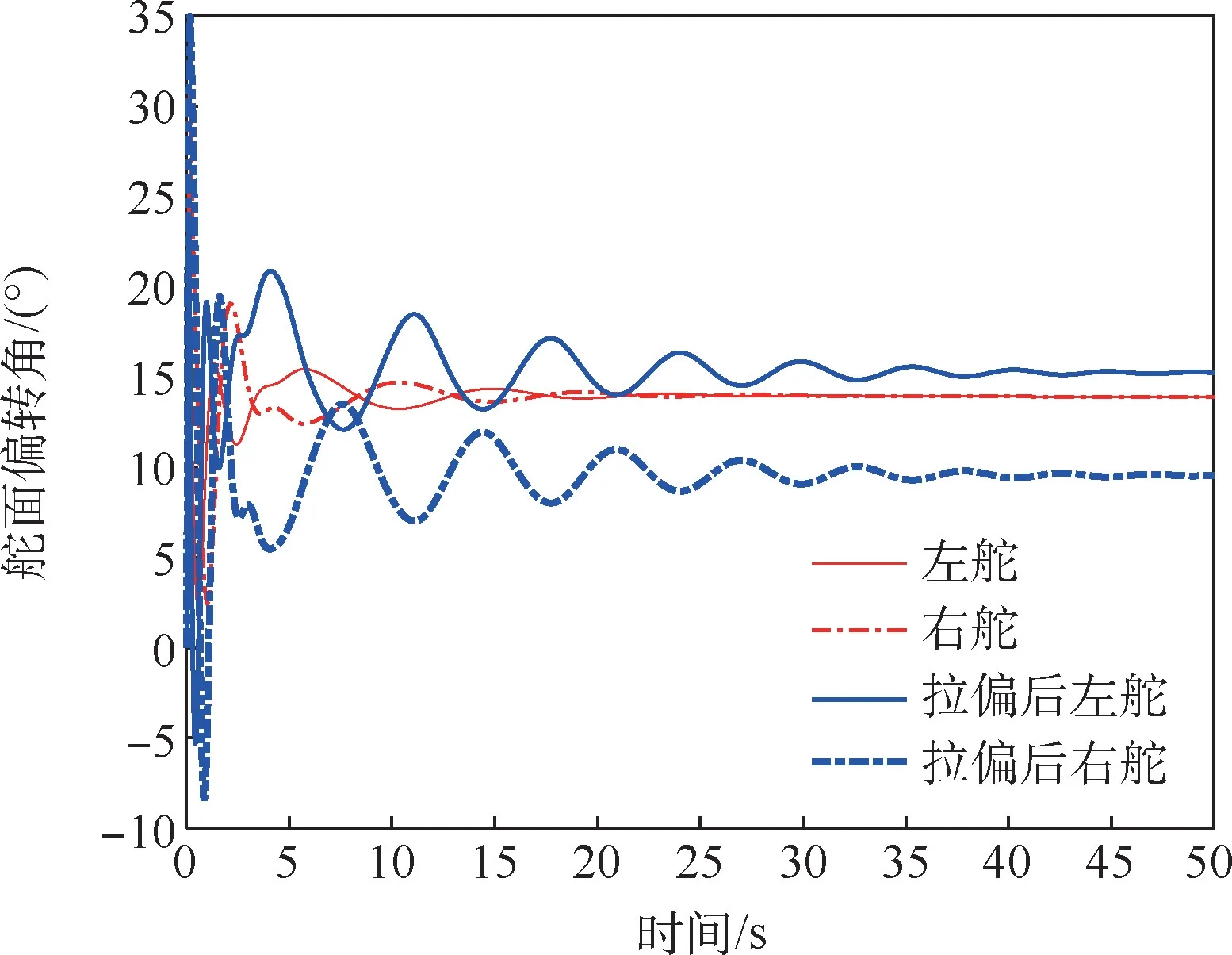
图10 方案1 舵面响应Fig.10 Aileron response of method

从仿真结果中可以看出,基于极点配置的方案在标称状态下,倾侧角能够稳定跟踪期望指令,侧滑角振荡收敛较快,系统舵偏响应调整迅速,除瞬态阶段无明显波动;但在参数拉偏后,控制器虽然稳定,但倾侧角出现较大的波动和静差,侧滑角和舵面的波动加剧且收敛变慢,系统性能鲁棒性较差,与特征根有界摄动分析结果吻合。

4.2 反馈解耦控制方案

工作点与前文保持一致,根据式(24)反馈增益为

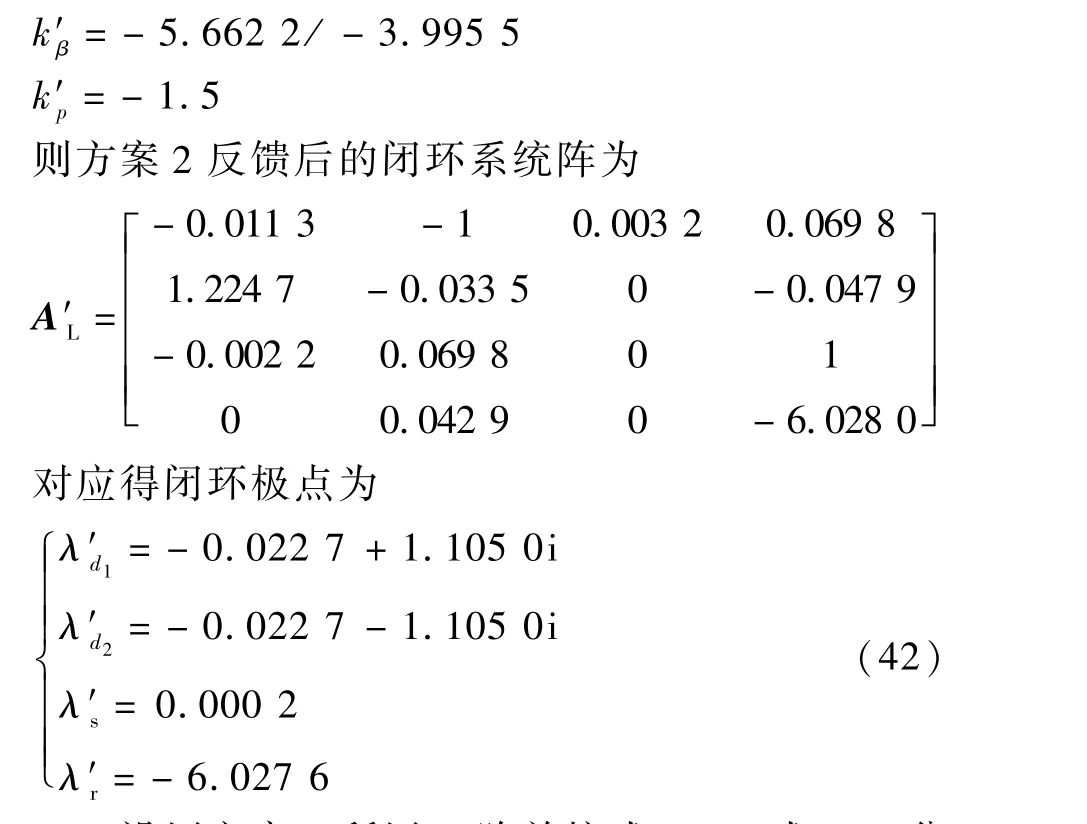
沿用方案1 所用R阵并按式(32)、式(33)分别求λ′d1、λ′r所对应的特征根有界摄动矩阵分别为

其对应特征根有界摄动系数为

与方案1 有显著不同,方案2 系统极点总的来看对参数摄动不敏感,这说明参数扰动对系统极点的影响很小,系统鲁棒性较强。 其特征根有界摄动系数要显著小于方案1 的矩阵范数,这一结果同样印证其对参数摄动不敏感。

同样在方案中对L′p项加入±25%的摄动,即在区间[ -7.535 0, -4.521 0]变化,系统极点随L′p变化的情况如图11 所示,其中线条越粗大代表L′p越大。

从图11 中可以看出,采用方案2 闭环后的系统,在加入±25% 的L′p参数摄动后,系统荷兰滚极点几乎不受影响,滚转阻尼极点受的影响有限,鲁棒性更强,这也与计算得到的Γ′r、Γ′d1结果一致。在与方案1 相同条件下进行闭环六自由度仿真,得到响应如图12 ～图14 所示。

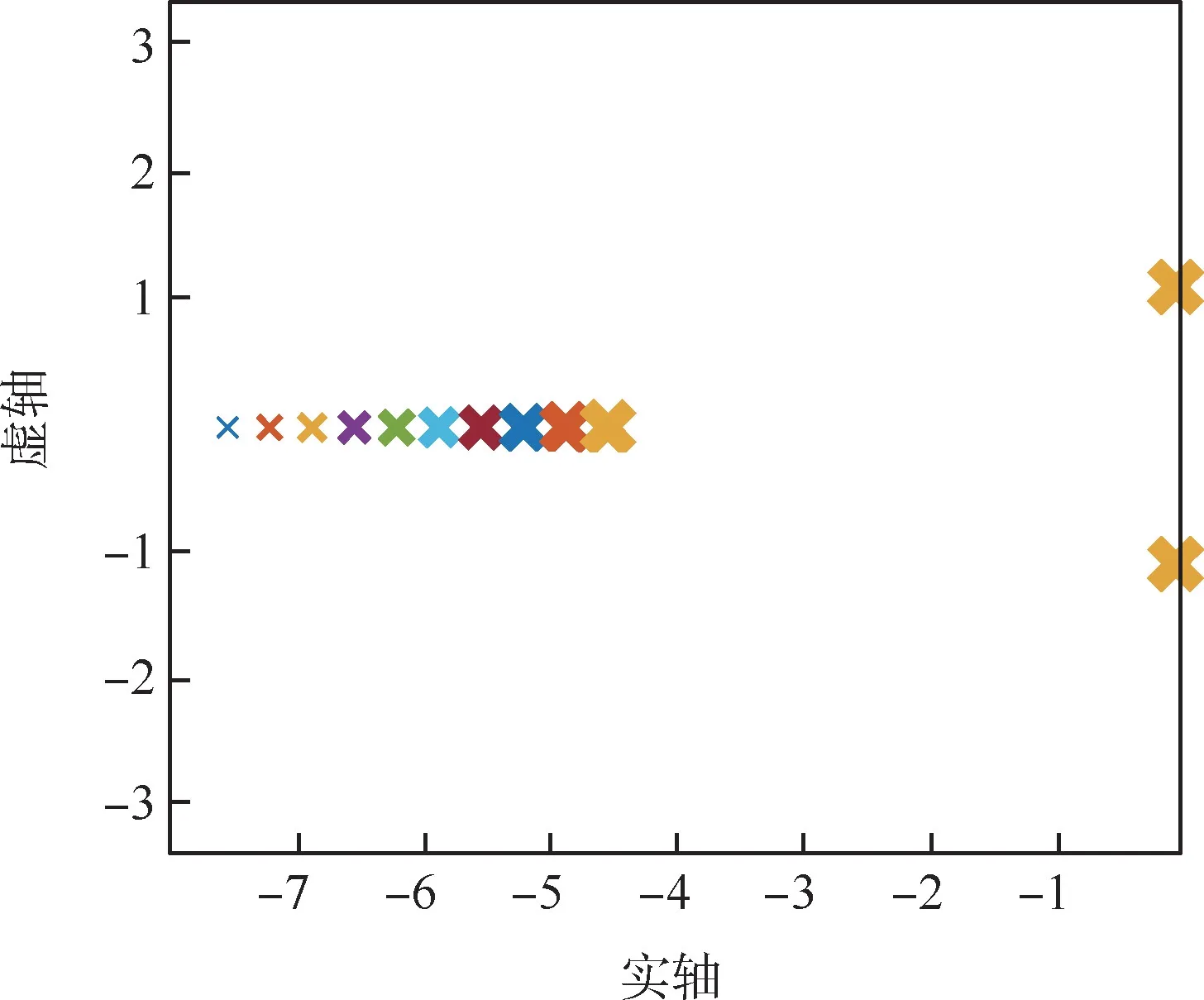
图11 方案2 极点受扰动的影响Fig.11 Poles of method 2 vary with uncertainties

图12 方案2 倾侧角响应Fig.12 Bank angle response of method 2

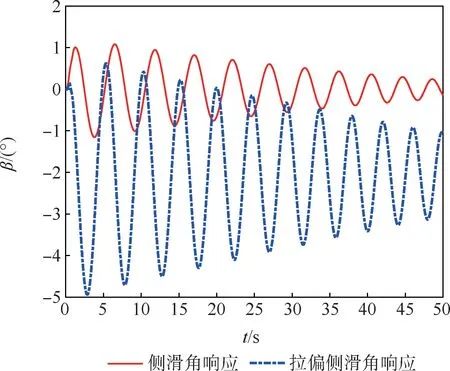
图13 方案2 侧滑角响应Fig.13 Sideslip angle response of method 2

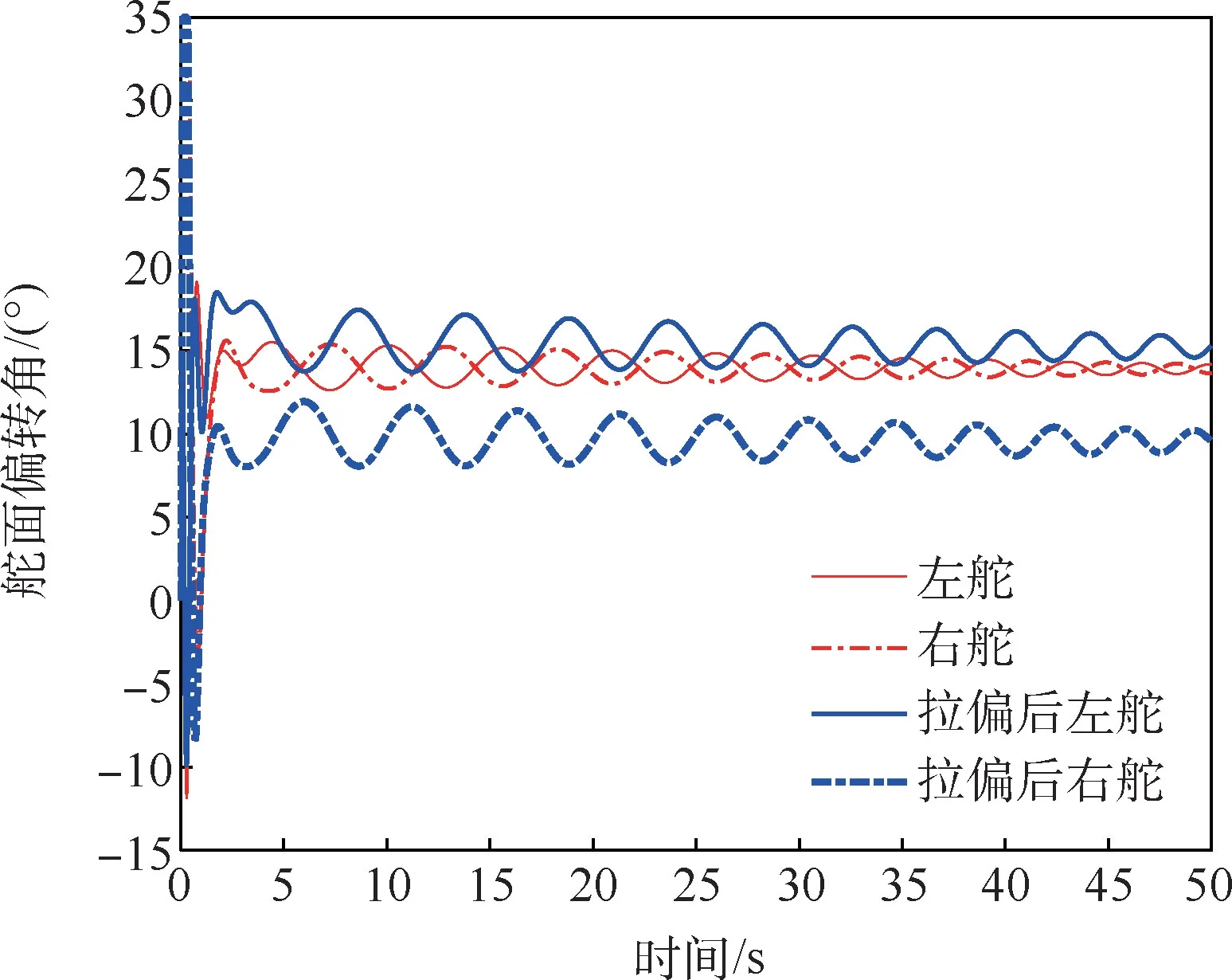
图14 方案2 舵面响应Fig.14 Aileron response of method 2

从仿真结果来看,由于偏航通道利用其本身静稳定性实现稳定,侧滑角呈现缓慢收敛的特点。但倾侧角的控制效果良好,调节时间在2 ～3 s内,且在极端干扰情况下仍能对飞行器实现有效控制,相比方案1 有更强的鲁棒性。

综合来看,对极点配置方案虽然实现了荷兰滚模态的快速镇定,但由于其高增益特性,导致鲁棒性下降,适用于模型精确情况。 而模态解耦方案的滚转与俯仰通道控制效果更好,其优势在于鲁棒性强,工程应用的潜力更大。

5 结 论

针对高超声速飞行器的双通道控制问题,本文提出了一种基于特征根有界摄动的鲁棒性分析方法,并给出了2 种实现双通道反馈控制的方案。

1) 给出了一种更为详细的荷兰滚阻尼预测式,特别是给出了交叉阻尼系数对荷兰滚阻尼的影响,进而引出了2 种双通道控制方案。 另外在精度上也得到了提升,全包线荷兰滚阻尼预测精度平均提升了15%,荷兰滚频率预测精度平均提升了25%。

2) 所提的反馈控制鲁棒性分析方法易于工程应用,引入的特征根灵敏度矩阵与特征根有界摄动矩阵计算简单,概念本身从矩阵特征根出发也便于使用经典控制理论研究系统规律。

3) 仿真表明,所提2 种控制方案可以利用副翼有效改善横侧向控制特性,实现双通道控制,参数拉偏的鲁棒性验证结果与特征根有界摄动分析结果吻合。