基于PSO-BP 神经网络的平流层风场短期快速预测

龙远 邓小龙 杨希祥 侯中喜

(国防科技大学 空天科学学院, 长沙 410073)

平流层是处于对流层与中间层之间、海拔高度为10 ～55 km 的大气空间[1],平流层内气流相对平稳、垂直对流小[2],是部署平流层飞艇、高空气球、高空太阳能无人机等临近空间低速飞行器执行对地观测、监视预警、通信中继、环境监测及科学研究等军民任务的理想环境[3-6]。

由于飞行速度低、动力系统弱、控制能力有限等约束,临近空间低速飞行器的飞行性能受其所处环境风场影响较大[7-8]。 例如,平流层飞艇的驻留能力直接取决于风场环境[9],而高空太阳能无人机的气动特性及续航里程也受到风场环境重要影响。 因此,开展平流层风场研究,获取准确的风场预测信息对于临近空间低速飞行器开展飞行任务规划、航迹规划和飞行控制都具有重要意义[10]。

目前,可用于平流层风速预测的方法主要包括2 类:数值天气预报方法和统计模型方法[11]。数值天气预报需要建立复杂的物理模型和庞大的计算系统,通过气象学理论和计算流体力学得到风速、风向、温度、湿度等气象要素的预测值。 而统计模型方法主要采用数学统计的思想,通过挖掘数据间存在的内在规律进行预测,此类方法包括时间序列法、卡尔曼滤波、神经网络等。 常规数值天气预报系统主要关注对流层内与人类社会经济活动密切相关的气象信息,平流层的风场预测没有得到足够的重视,精度还有待提高[12],且对飞行器研制与应用部门的环境保障要求高。 因此,在平流层风场预测中,通常采用统计模型的方法。

国内外学者对统计模型方法在风场预测中的应用展开了大量研究。 文献[13]通过本征正交分解(POD)方法建立了风场降阶模型,再利用傅里叶级数拟合对平流层风场进行预测;文献[14]利用POD 方法对具有桥塔风效应的风场进行了简化模拟,将POD 型谱表示法取代原型谱表示法,物理意义明确且可通过模态截断节省计算量;文献[15]根据历史风场统计数据建立了韦伯分布模型,利用韦伯分布和累积函数对历史数据进行预测和反算,验证了将韦伯分布应用于风场数据统计的合理性;文献[16]提出了一种基于高斯过程(Gaussian processes,GP)的风速预测模型,将其与支持向量机、最小二乘支持向量机和BP 神经网络进行比较,仿真结果表明,基于GP 的风速预测模型具有很好的稳定性,能够满足预测精度的要求;文献[17]建立了高斯过程回归和粒子滤波相结合的短期风速预测模型,实现了对历史风速序列异常值的在线动态检测与修正;文献[18]利用平流层风场纬向风存在一定周期性和规律性的特点,分别采用傅里叶级数拟合方法和BP 神经网络算法对风场快速预测进行了研究,并对2种方法的预测误差与预测精度进行了分析;文献[19]研究了数据增强和自校正设计在平流层风场建模中的应用,将美国国家海洋与大气管理局提供的风场预报数据和高空气球实测风场数据相结合,构建了可用于高空气球轨迹规划的风场预测模型。

上述研究大多专注于对流层内的风场预测问题,在平流层风场预测方面的研究较少,且较多集中于短期单点预测,无法满足临近空间低速飞行器进行路径规划所需的区域风场环境。 在已有研究的基础上,本文根据历史风场数据,先采用主成分分析(principal component analysis, PCA)法对数据进行降维处理,再通过训练BP 神经网络对风场进行预测,并利用粒子群优化(partical swarm optimization, PSO)算法对BP 神经网络进行优化。 针对临近空间低速飞行器飞行区域广、单点预测风场数据无法满足长时间飞行需求,进一步研究Biharmonic 样条曲面插值方法对多点风场预测结果进行空间插值,构建了平流层区域预测风场,能够为长航时临近空间低速飞行器提供数据支撑。

1 平流层风场数据降维方法

基于统计模型的风场建模方法需要从海量历史环境数据开始分析,这类数据的数据量大、特征不清晰,有必要预先进行降维处理,在保证原有信息损失不大的前提下,尽可能降低数据量的大小。PCA 则是最常用的一种降维方法。 PCA 能够找出数据里面最主要的方面,用数据里最主要的方面来代替原始数据。

假设有某一坐标点记录的n×m维历史风场数据集X,数据集共有m个风场数据(x1,x2,…,xm),每个风场数据都是n维列向量,代表着坐标点某一时刻的风速在不同采样高度处的取值,n为采样点总个数。 为了降低风场数据量的大小,需要对其进行降维处理,在降维的过程中,要获得原始数据新的表示空间,需要对原始数据进行线性变换(基变换),矩阵表示如下:

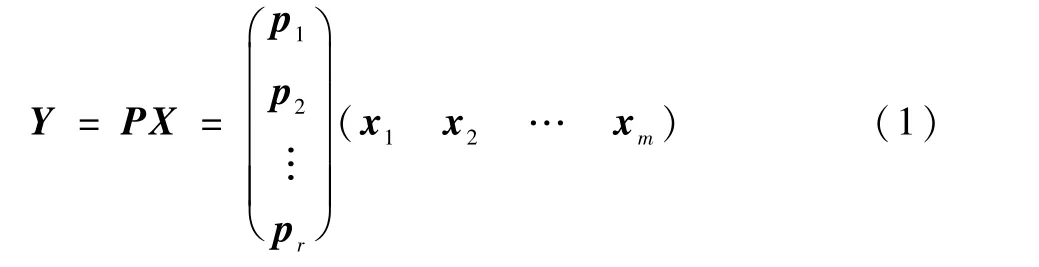
式中:Y为风场数据样本在新空间的表示;P为r×n维变换矩阵;X为原始风场数据样本;pi表示第i个基;xj表示第j个原始风场数据。

选择不同的基可以对一组数据给出不同的表示,同时,当基的数量少于原始样本本身的维数时,则可以达到降维的效果,PCA 就是要找到能够最大限度保留原有数据信息的一组基P,具体分析步骤如下:

步骤1 样本中心化处理。 为了简便运算,需要对风场数据样本进行中心化处理,得到新的数据样本:

步骤3 求特征值及特征向量。 求解得到新风场数据样本协方差矩阵的特征值λ1,λ2,…,λn,以及对应的单位特征向量ϕ1,ϕ2,…,ϕn。

步骤4 确定降维维度r。 将第r个主成分保留的信息称作相对模态能量,表示为

根据风场数据的信息保留量(即累积模态能量的大小)来确定选取的主成分个数r,该数值即是降维后的数据维度,r＜n。

步骤5 求新变换矩阵P。 按风场数据样本协方差矩阵特征值的大小将前r个特征值对应的特征向量从上向下按行排列成矩阵,该矩阵就是要求的变换矩阵P。

Y=PX即为降维到r维后的风场数据。

2 基于神经网络的平流层风场预测方法

在对风场数据进行降维处理后,数据量大大减小,可用神经网络学习风场的变化特征以对未来短期风场进行快速预测。 本节研究基于BP 神经网络的风场预测方法,并通过具备全局寻优特性的PSO 算法来改进容易陷入局部最优的BP 神经网络。

2.1 BP 神经网络风场预测模型

本节建立的风场预测模型使用的神经网络包含输入层、隐含层和输出层3 层,其中输入层的神经元个数根据降维后的风场数据维数设置为3,输出层神经元个数设置为1,隐含层神经元个数根据经验公式设置为12,经验公式如下:

式中:q为隐含层神经元个数;k和l分别为输入层和输出层神经元个数;a为常数,a∈[1,10]。

如图1 所示,BP 神经网络每个神经元都与上一层的所有神经元相连,隐含层和输出层每个神经元的输出与输入之间的关系如下:

图1 神经网络结构Fig.1 Structure of neural network

式中:xi为神经元的输入信号,即风场数据;ωi为输入信号的权值;θ为神经元的阈值;f(·)为激活函数。

本节使用的激活函数为Sigmoid 函数:

假设在进行降维处理后,有r×m维风场数据Y=(y1,y2,…,ym),将其分为r个行向量,利用神经网络分别对这r个行向量的数据变化特征进行学习,神经网络训练集的输入数据和输出数据的构建如图2 所示,将m个风场数据分成m-3组训练数据,每组训练数据包含3 个输入和1 个输出。

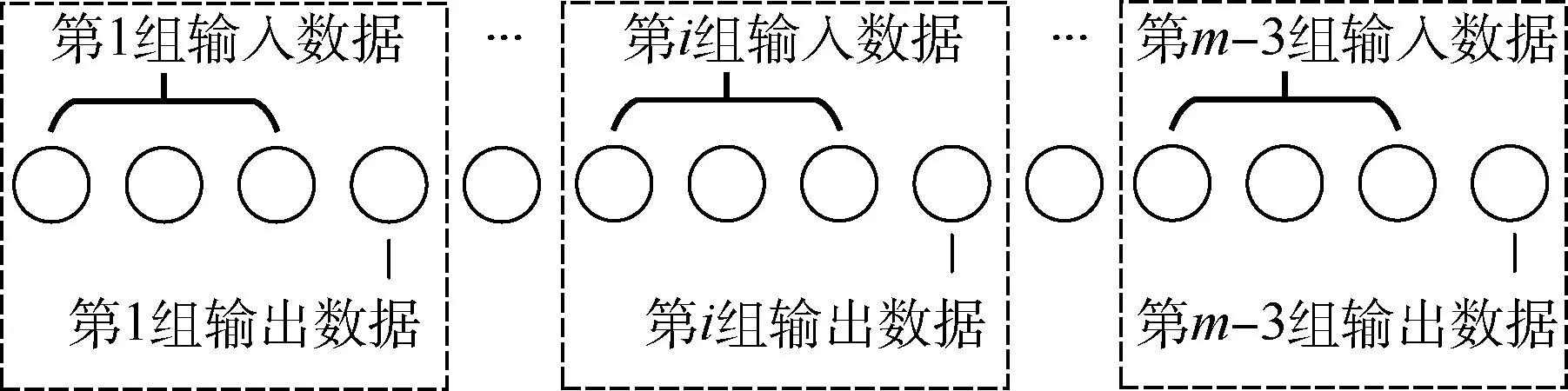
图2 神经网络的输入和输出Fig.2 Input and output of neural network

2.2 PSO-BP 神经网络风场预测模型

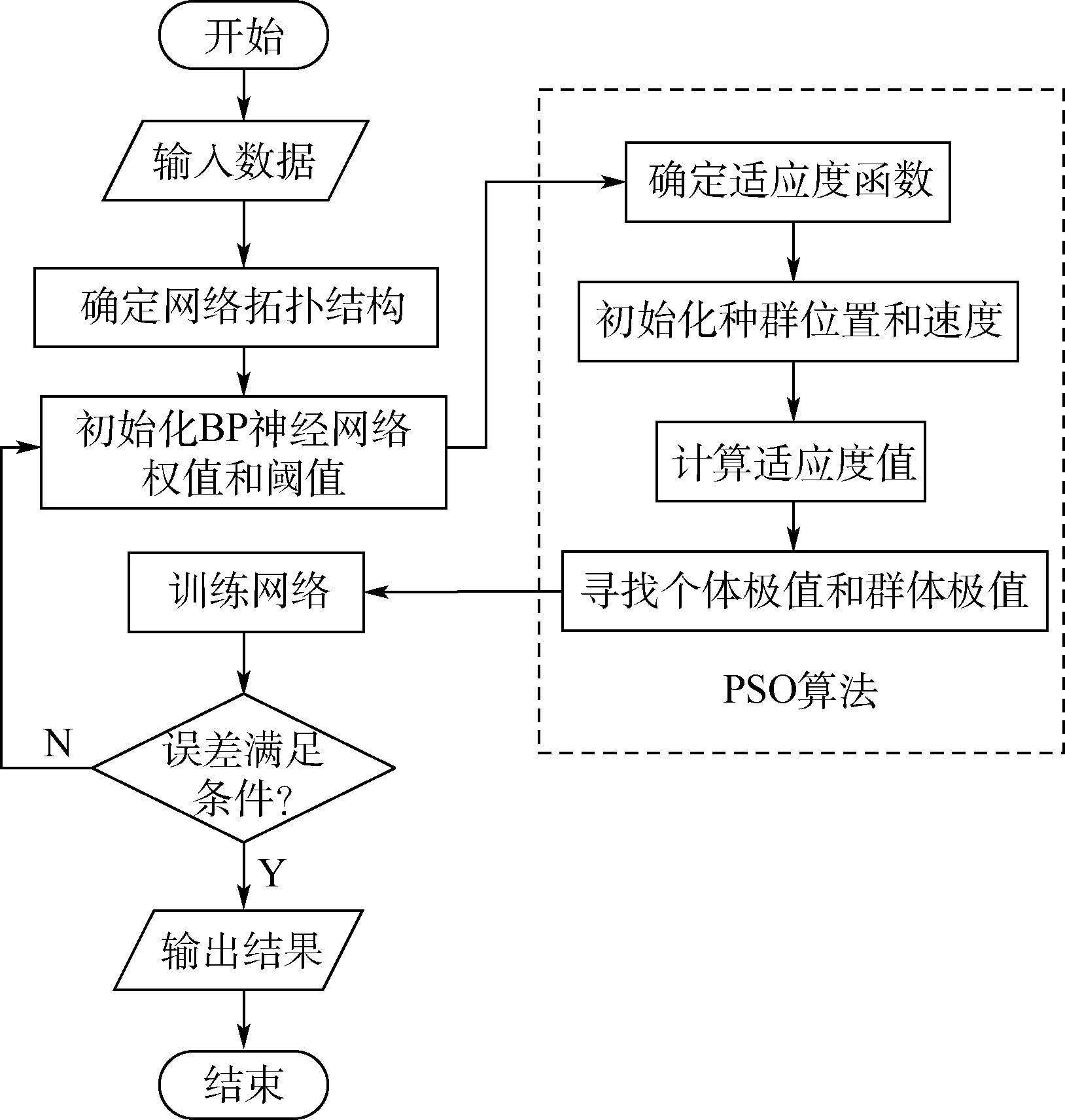
图3 PSO 算法的BP 神经网络原理Fig.3 Schematic diagram of BP neural network optimized by particle swarm optimization algorithm

本节以神经网络训练过程中的输出误差作为PSO 算法的适应度函数,先随机地初始化一个粒子群体,每个粒子包含一组神经网络权值和阈值的数据,通过更新公式不断迭代每个粒子的取值,最终使得适应度函数值最小。

PSO 算法速度更新如下:

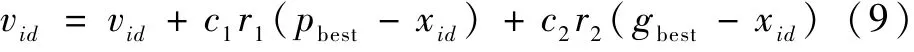
式中:c1、c2为学习因子;r1、r2为(0,1)内的随机数;pbest为每个粒子当前找到的最优解;gbest为整个种群当前找到的最优解。

PSO 算法位置更新如下:

本节使用的PSO 算法种群数量为50,2 个学习因子均设置为2,迭代步数设置为100。

3 结果与分析

低纬度海洋地区是开展临近空间低动态飞行器应用的理想场所,本节采用4 个地点的历史风场数据作为神经网络的训练集,坐标分别为

A(112°E,17° N)、B(113° E,9° N)、C(115° E,10°N)、D(116°E,10°N)。 每个坐标点的数据均为250 ×3 652 的数组,其中250 表示高度维,代表在该坐标点250 个不同的高度处取得风场数据,3 652表示时间维,代表每个坐标点有5 年的历史风场数据,每天0 时和12 时分别采样,一共3 652 组采样数据。

3.1 数据降维结果与验证

利用PCA 法可以求解出风场数据降维后不同阶数能够保留的原始数据信息量比重。 本节以相对模态能量和累积模态能量这2 项指标来衡量模态阶数还原原始数据的能力,并根据各阶模态能量,选择合适的降维阶数,使得降维后的数据在数据量减小的情况下依然能够保留大部分风场信息。

以A点数据为例,分析降维数据的数据量降低情况和数据信息保留情况。 考虑到平流层浮空器主要是在20 km 附近持久驻留,因此,需要重点关注该高度附近的风场信息。 该高度附近的风场与10 km 附近的风场有明显区别,不宜统一使用降维方法进行处理。 为此,提出了分层降维方法,即将整个风场在高度上进行分层处理,即分为2个部分:5 ～15 km 和15 ～30 km。 15 km 以下的区域主要属于对流层,风场相对较大,且风场随高度变化较明显;而15 km 以上的区域风场变化较小。 对这2 部分风场在东西和南北方向上分别开展降维处理并分析得到了如下结果:

他的视线掠过女孩，望向了跟在女孩后面的滑翔翼。它的颜色灰不溜秋的，结构和做工都要粗糙着许多，但它的特殊性，在于它的翼面尤其宽大，比自己的几乎要宽出二分之一。

1) 东西方向上5 ～15 km:10 阶数据保留原数据信息量为99.91%。

2) 东西方向上15 ～30 km:6 阶数据保留原数据信息量为99.96%。

3) 南北方向上5 ～15 km:11 阶数据保留原数据信息量为99.95%。

4) 南北方向上15 ～30 km:7 阶数据保留原数据信息量为99.93%。

3.1.1 东西方向风场降维

由图4 和图5 可知,在东西方向上,15 ～30 km的风场特征比较明显,因此,前6 阶模态所包含的能量之和已经达到了99.96%,而5 ～15 km 的风场需要前10 阶模态,才能使得能量总和达到99.91%。 可以用5 ～15 km 前10 阶的数据和15 ～30 km 前6 阶的数据代替原有250 阶的数据,将两部分风场合并后,数据量仅为原有数据量的6.4%。

图4 海拔5 ～15 km 东西方向风场数据降维后的第n 阶相对模态能量及前n 阶累积模态能量Fig.4 The n-th order relative modal energy and the first n-order cumulative modal energy of east-west wind field data after dimensionality reduction between 5 km and 15 km

图5 海拔15 ～30 km 东西方向风场数据降维后的第n 阶相对模态能量及前n 阶累积模态能量Fig.5 The n-th order relative modal energy and the first n-order cumulative modal energy of east-west wind field data after dimensionality reduction between 15 km and 30 km

在PCA 法进行了数据降维处理之后,将降维后的风场数据与实际风场数据进行了对比验证。由图6 可知,东西方向降维后的风场与实际风场数据的偏差较小,降维数据基本上与原有数据吻合,高度保留了原有数据的特征。

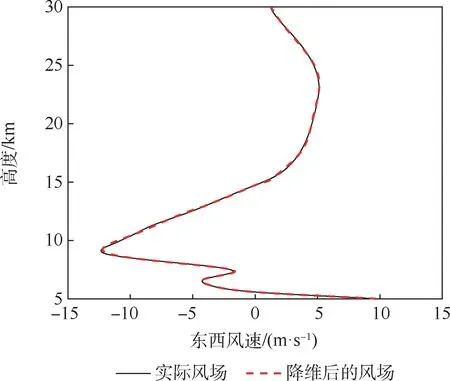
图6 东西方向上降维后的风场数据与实际风场数据对比Fig.6 Comparison of east-west wind field data after dimensionality reduction and actual wind field data

3.1.2 南北方向风场降维

由图7 和图8 可知,南北方向上两部分的风场降维数据,即前11 阶模态和前7 阶模态,所包含的能量之和分别为99.95%和99.93%,南北方向上的风场数据可以用降维后总共18 阶的数据来代替原有250 阶数据,数据量仅为原有数据量的7.2%。

图7 海拔5 ～15 km 南北方向风场数据降维后的第n 阶相对模态能量及前n 阶累积模态能量Fig.7 The n-th order relative modal energy and the first n-order cumulative modal energy of north-south wind field data after dimensionality reduction between 5 km and 15 km

图8 海拔15 ～30 km 南北方向风场数据降维后的第n 阶相对模态能量及前n 阶累积模态能量Fig.8 The n-th order relative modal energy and the first n-order cumulative modal energy of north-south wind field data after dimensionality reduction between 15 km and 30 km

由图9 可知,南北方向降维后的风场与实际风场数据基本吻合。 因此,PCA 法在减小数据量的同时可以保留大部分原有数据的信息。 在后续的神经网络处理过程中,风场数据就可以使用降维后的数据来代替。

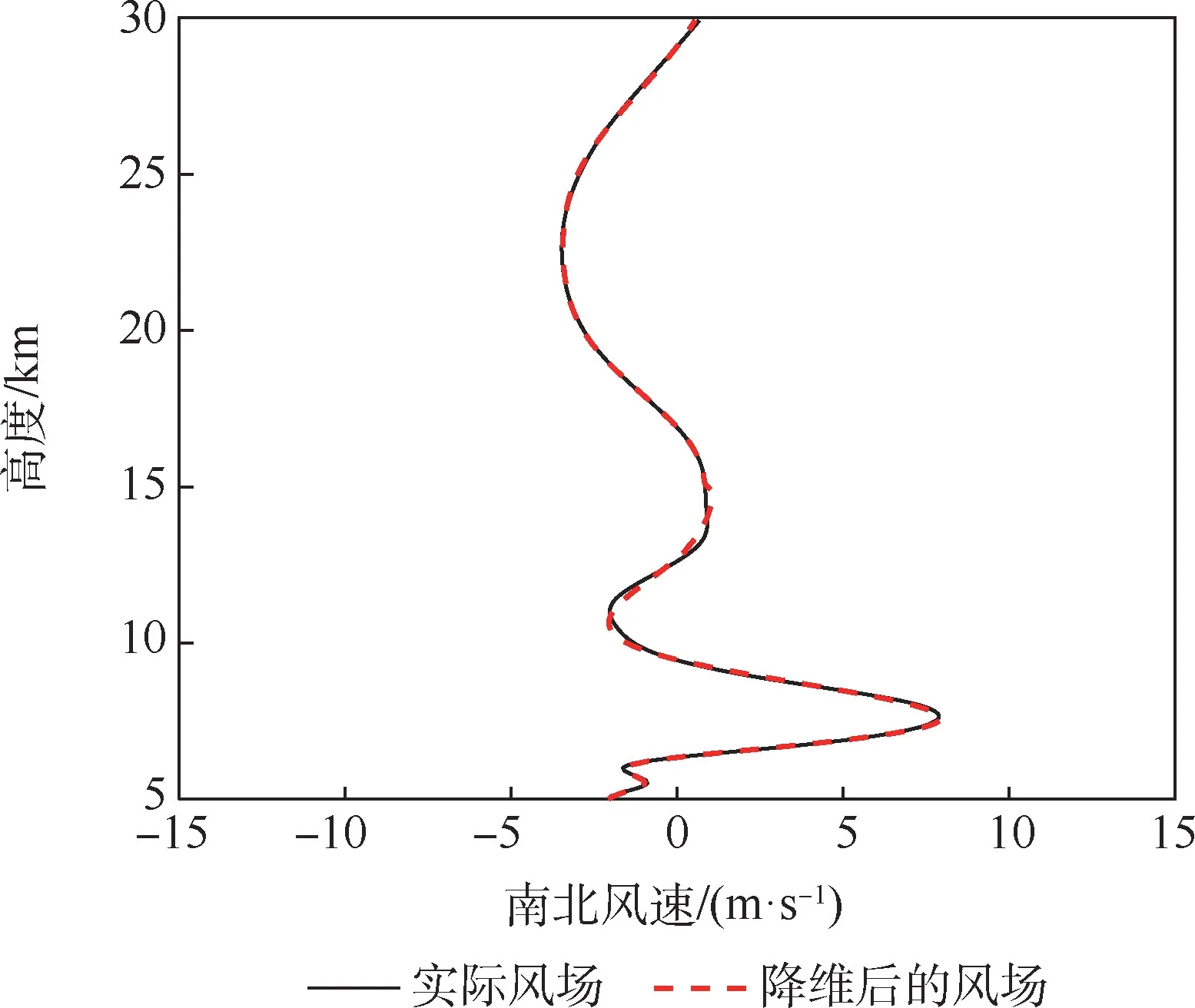
图9 南北方向上降维后的风场数据与实际风场数据对比Fig.9 Comparison of north-south wind field data after dimensionality reduction and actual wind field data

3.2 神经网络预测结果分析

根据临近空间低速飞行器执行任务所需要的工作高度特点[20],使用5 ～30 km 的数据分别对BP 神经网络和PSO-BP 神经网络进行训练,使用训练后的神经网络对未来风场进行预测,随机选取了10 次预测结果与实际风场进行对比。

3.2.1 东西方向风场预测

由图10 ～图12 可看出,在东西方向上,BP神经网络和改进后的PSO-BP 神经网络均能对风场进行较好的预测,但由于BP 神经网络采取的是梯度下降算法,偶尔会得到局部最优的结果,使得风场预测结果与实际风场偏差较大;而经PSO算法优化的PSO-BP 神经网络能够更好地寻找全局最优值,获得更好的风场预测效果。2 种预测模型的东西方向风场预报误差对比分析表明,采用PSO 算法改进后的PSO-BP 神经网络风场预测模型平均预测误差要小于BP 神经网络模型的平均误差,在15 km 以上区域,二者的平均误差都小于2 m/s。

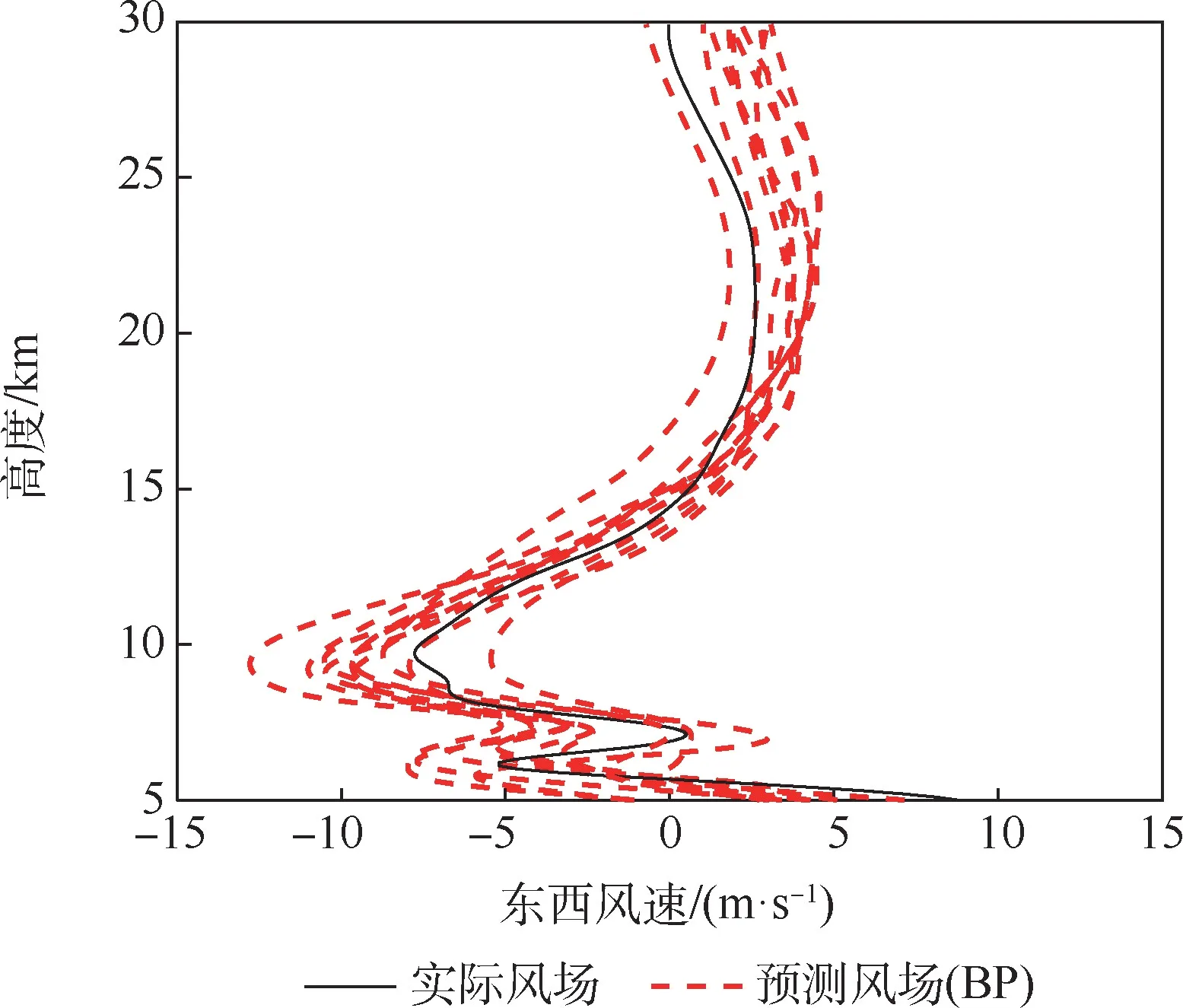
图10 东西方向上BP 神经网络10 次预测结果与实际风场对比Fig.10 Comparison of 10 prediction results of BP neural network and actual wind field in east-west direction

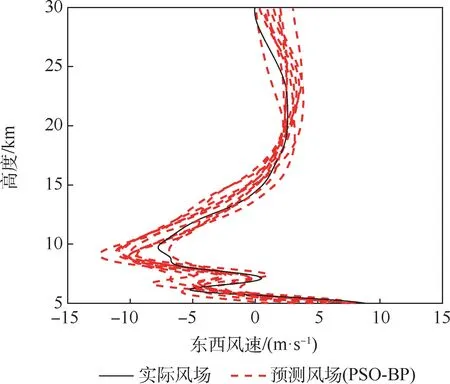
图11 东西方向上PSO-BP 神经网络10 次预测结果与实际风场对比Fig.11 Comparison of 10 prediction results of PSO-BP neural network and actual wind field in east-west direction

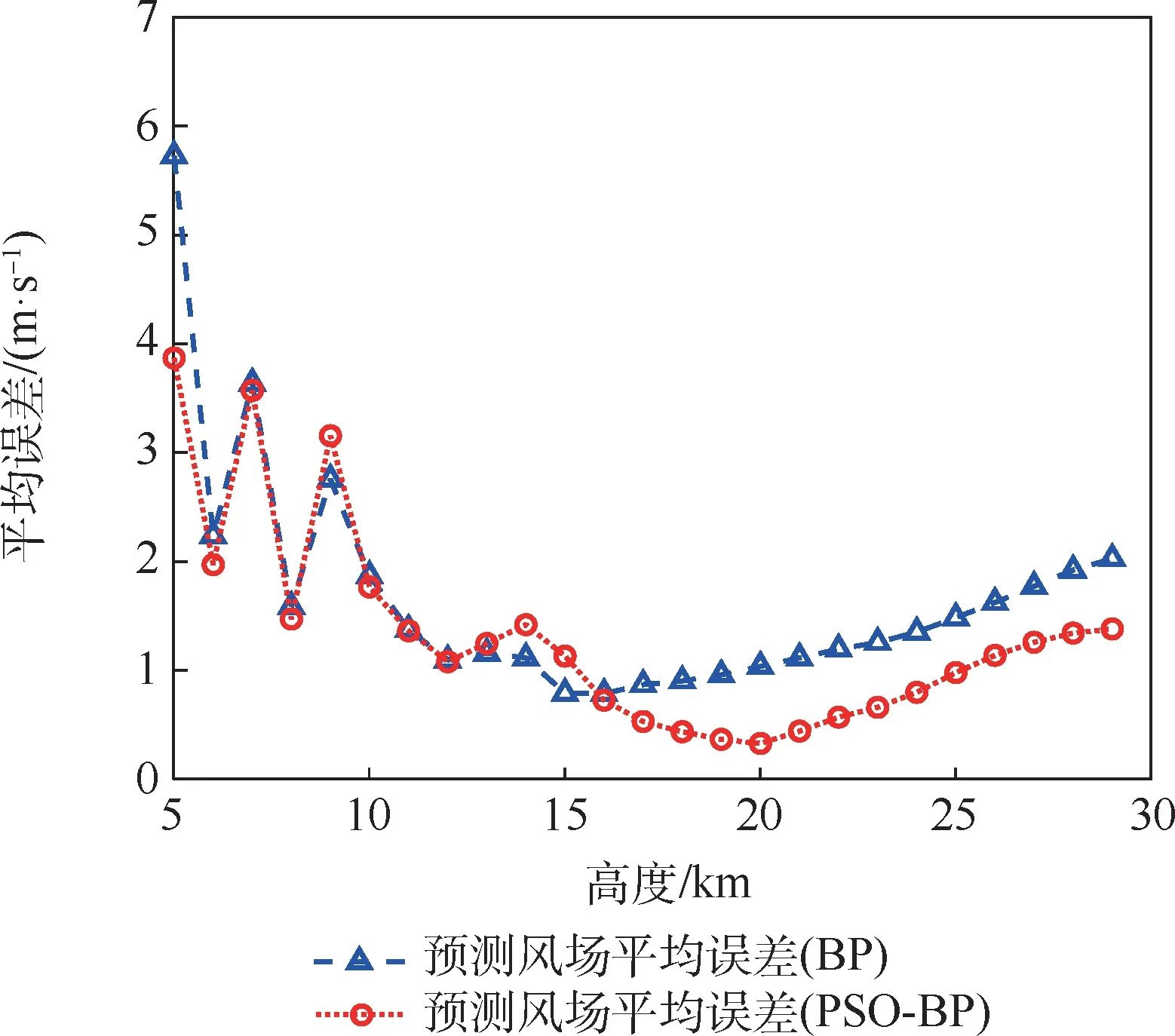
图12 东西方向上2 种神经网络10 次预测结果平均误差对比Fig.12 Comparison of average error of 10 prediction results for two kinds of neural networks in east-west direction

3.2.2 南北方向风场预测

由于平流层独特的风场环境,其南北方向上的风速分量一般较小,在采用神经网络对其进行预测时,效果并没有在东西方向上明显。 由图13 ～图15 可看出,BP 神经网络和改进后的PSO-BP 神经网络对南北方向上的风场的预测效果均不如东西方向,但相较于BP 神经网络,PSO-BP 神经网络仍然能够获得更好的预测效果。

图13 南北方向上BP 神经网络10 次预测结果与实际风场对比Fig.13 Comparison of 10 prediction results of BP neural network and actual wind field in north-south direction

图14 南北方向上PSO-BP 神经网络10 次预测结果与实际风场对比Fig.14 Comparison of 10 prediction results of PSO-BP neural network and actual wind field in the north-south direction

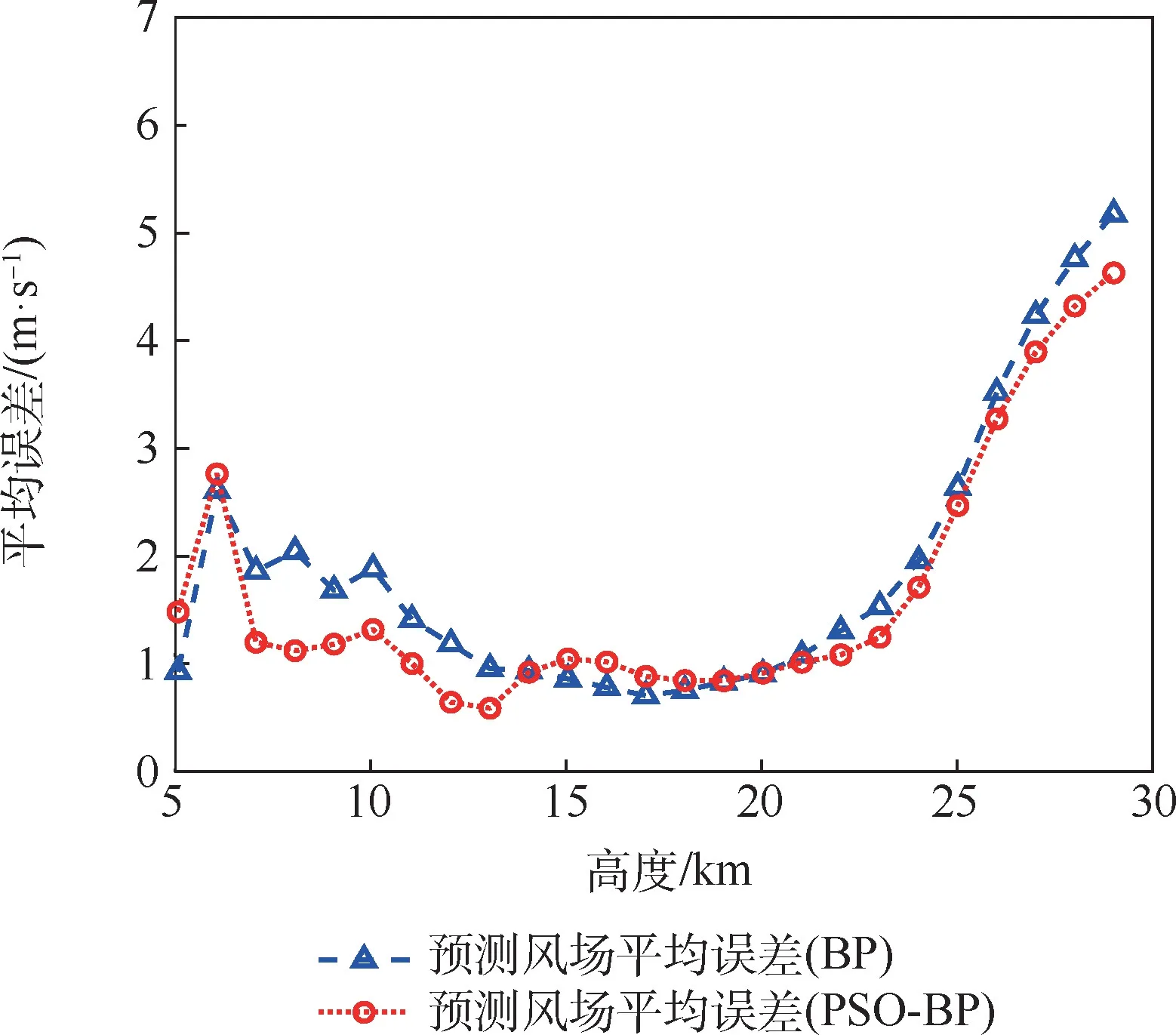
图15 南北方向上2 种神经网络10 次预测结果平均误差对比Fig.15 Comparison of average error of 10 prediction results for two kinds of neural networks in north-south direction

2 种预测模型的南北方向风场预报误差对比分析表明,在25 km 高度范围以下的预测效果较好,2 种模型预测结果差异不明显;在25 km 以上的区域预测2 种模型误差均快速增加,平均误差都超过了2.5 m/s。

3.3 区域风场构建分析

平流层飞艇和高空飞机的路径规划需要广大范围的风场信息,高空气球区域驻留也并非总是能保持在给定点附近,因此,需要对区域多点风场进行建模。

在使用神经网络对风场进行预测之后,能够得到多点随高度变化的风速数据,本节使用的数据是4 个坐标点A(112°E,17°N)、B(113°E,9°N)、C(115°E,10°N)、D(116°E,10°N)的风场预测结果,用Biharmonic 样条曲面插值方法对每一高度处的数据进行插值处理,能够得到三维空间的风速情况。 针对临近空间低速飞行器典型工作高度20 km 进行风场构建仿真,仿真结果如图16和图17 所示。

图16 东西方向上20 km 高度的区域风速示意图Fig.16 Schematic diagram of regional wind speed in east-west direction at 20 km

图17 南北方向上20 km 高度的区域风速示意图Fig.17 Schematic diagram of regional wind speed in north-south direction at 20 km

由图16 和图17 可知,在对风场数据进行插值处理后,任一高度剖面均能得到在不同经纬度的风速变化图,在平流层浮空器轨迹规划等问题中,给出任一经纬高坐标,构建的风场模型均能得到风速值在东西方向和南北方向上的分量。 因此,便构建了三维空间的区域风场模型,可以获取区域内任意点处的风速数据。

临近空间低速飞行器在执行轨迹规划或区域驻留任务时,往往需要在较大范围内飞行。 因此,飞行器在区域风场模型下的轨迹仿真要比单点风场模型下的仿真更符合实际飞行情况。 下面根据平流层飞艇的动力学方程[21]分别在区域风场模型和单点风场模型下仿真飞艇的飞行轨迹。 以坐标原点作为仿真初始点,平流层飞艇在浮力作用下自然升空,海拔高度达到20 km 后降落回收,其飞行轨迹如图18 所示。

由图18 可知,在仿真初始阶段,区域风场模型和单点风场模型下的飞艇飞行轨迹区别不大。但是,当飞艇逐渐远离初始点之后,2 种风场模型得到的飞行轨迹便显现出较大差异,最终二者的水平位移误差达到了13.3 km。

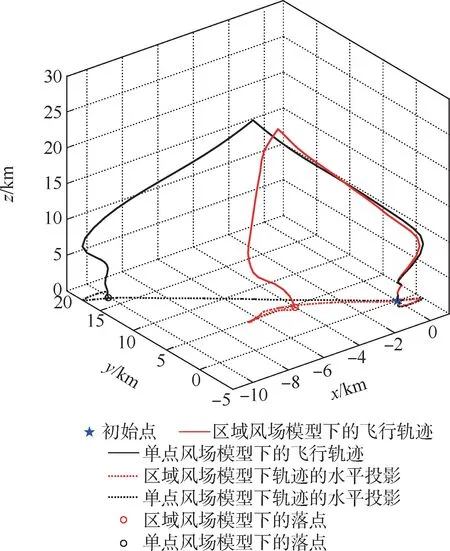
图18 两种风场模型下飞行器的轨迹示意图Fig.18 Schematic diagram of trajectory for aircraft under two wind field models

4 结 论

1) 采用PCA 法对5 年的历史风场数据进行降维处理,将250 阶的风场数据分别降至16 阶和18 阶,原始数据信息保留率达到99%以上。 使用降维后组成的新数据代替原有数据,降低了数据量,提高后续工作的计算效率。

2) 采用具有全局寻优特性的PSO 算法改进了易陷入局部最优的BP 神经网络,并通过改进后得到的PSO-BP 神经网络和传统BP 神经网络对未来风场进行预测。

3) 对2 种神经网络风场预测模型的预测精度与预测误差进行了分析,发现相较于基于梯度下降法的BP 神经网络,经过PSO 算法优化的BP神经网络训练得到的神经网络参数能够更好地反映风场的变化规律,风场预测精度要高于传统的BP 神经网络。

4) 采用Biharmonic 样条曲面插值方法对单点的神经网络风场预测结果进行插值处理,构建了一个三维空间的区域风场模型,可以获取区域内任意点处的风速数据,区域预报可有效提高飞行轨迹仿真结果精度。