二次曲线相交弦与切割线定理及其应用

厦门大学附属实验中学 (363123) 吴赛瑛

一般的二次曲线可表示为Ax2+By2+Cxy+Dx+Ey+F=0,其中A、B、C不同时为0.本文主要探讨一般二次曲线相交弦与切割线的斜率性质及其在高考题、省市质检题的应用.

定理已知点S不在二次曲线Γ:Ax2+By2+Cxy+Dx+Ey+F=0上，过点S的两条直线l1、l2分别交曲线Γ于P、Q和M、N，其中l1、l2的斜率分别为k1、k2(k1≠k2).若|PS||QS|=|MS||NS|，则当A=B,C≠0时，k1k2=1；当A≠B,C=0时，k1+k2=0.

证明：设S(x0,y0)，则l1、l2的方程分别为y-y0=k1(x-x0)，y-y0=k2(x-x0).设P(x1,y1)，Q(x2,y2)，M(x3,y3)，N(x4,y4)，联立

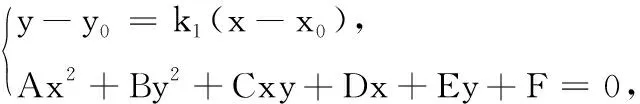
=(k12+1)(x1-x0)(x2-x0)=(k12+1)[x1x2+x02-x0(x1+x2)]

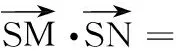
(1)求C的方程；

(2)对比二次曲线的一般方程的系数，可知A≠B,C=0，又|TA|·|TB|=|TP|·|TQ|，由本文定理可知直线AB的斜率与直线PQ的斜率之和kAB+kPQ=0.

例2 (湖南省2022年高三六校联考)已知抛物线C：y2=2px(p>0)的焦点为F，过点F的直线交抛物线C于P，Q两点，且直线PQ垂直于x轴，O为坐标原点，△OPQ的面积为2．

(1)求抛物线C的方程；

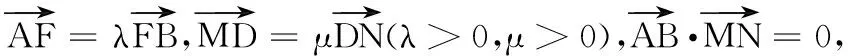
解：(1)易得y2=4x；(过程略)