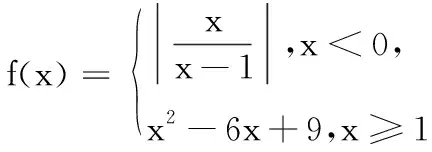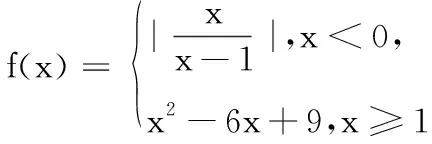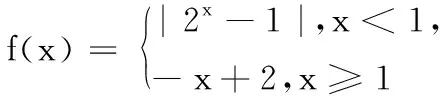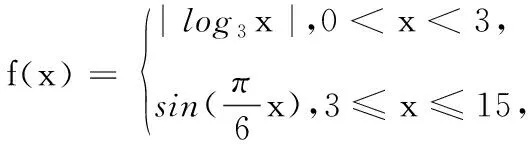函数“等值问题”变式探究
2022-11-08江苏省海门中学226100
江苏省海门中学 (226100) 张 婕
函数“等值问题”是指“已知函数在多个自变量处的的函数值相等,这些自变量称之为‘等值点’,求关于等值点的某个代数式的值、最值、范围或参数的取值范围等”的一类问题.函数“等值问题”在近年高考或各地模拟试题中高频出现,往往处于数学试卷客观压轴题的位置,利用函数的图象直观可使问题的解决明朗化,所以也是培养和形成直观想象数学核心素养的良好载体.
1、试题重现
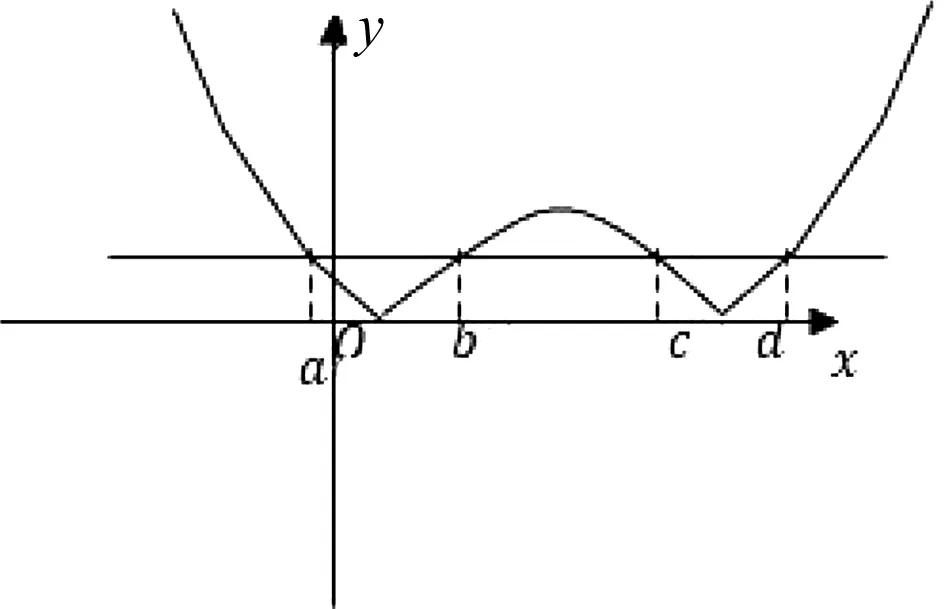
已知函数y=|x2-2x-1|的图象与直线y=m(m∈R)有四个交点,且这四个交点的横坐标分别为a,b,c,d满足a 设f(x)=|x2-2x-1|,将已知条件“函数y=|x2-2x-1|的图象与直线y=m(m∈R)有四个交点,且这四个交点的横坐标分别为a,b,c,d”,进行转译为f(a)=f(b)=f(c)=f(d)=m,是典型的函数“等值问题”.作出函数y=|x2-2x-1|的图象与直线y=m,利用函数图象的对称性求得a+b+c+d的值,利用求根公式用变量m表示出函数2(d-a)+(c-b),然后利用导数研究函数的单调性解得2(d-a)+(c-b)的最大值. 图1 解:在同一直角坐标系内作出函数y=|x2-2x-1|的图象与直线,如图1. 函数“等值问题”是一类函数零点或方程的根等问题的延伸,借助函数图象,数形结合解答问题,考查数学抽象、直观想象及逻辑推理等数学核心素养在解题中的应用,多数情况下承载着高考函数客观压轴题的重任,比如,2020年高考数学天津卷选择题压轴题第9题就是一个典型例子: 求解函数“等值问题”的基本思路是:分析题意,从中挖掘出函数的奇偶性、单调性、对称性及不变性等性质,结合函数式的特点及函数的相关性质,作出函数的图象,数形结合有效快速地解答问题. 若改变一下母题第二个空的问题,将求“2(d-a)+(c-b)的最大值”变为求“2(d-a)+(c-b)的取值范围”,可有: 变式1 已知函数y=|x2-2x-1|的图象与直线y=m(m∈R)有四个交点,且这四个交点的横坐标分别为a,b,c,d满足a 若改变母题中的解析式,将母题中分段函数的两段分别是“分式型”解析式和“二次函数型”解析式,求关于“等值点”的代数式的值,可有: 图2 若改变母题中的解析式,将母题中分段函数的两段分别是“指数型”解析式和“一次函数型”解析式,求关于“等值点”的代数式的取值范围,可有: A.(0,1) B.(1,2) C.(2,4) D.(4,6) 图3 由图3可知-2 若改变母题中的解析式,将母题中分段函数的两段分别是“对数型”解析式和“二次函数型”解析式,求关于“等值点”的代数式的最值,可有: 图4 若进一步改变母题中的解析式,将母题中分段函数的两段分别是“对数型”解析式和“三角函数型”解析式,分别求关于“等值点”的代数式值和取值范围,可有: 图5 解析:设f(x1)=f(x2)=f(x3)=f(x4)=t,在同一直角坐标系内作出函数f(x)的图象与直线y=t,如图5,则由题意可知直线02、解法探析
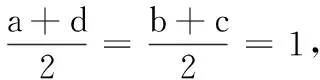


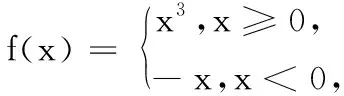

3.试题变式