特征值理论在稳定性预测中的应用研究进展综述

孙晓峰，董旭，张光宇，王卓，孙大坤，*

1. 北京航空航天大学 能源与动力工程学院，北京 100191 2. 北京航空航天大学 航空发动机研究院，北京 100191

长期以来，中国在航空发动机领域的发展始终徘徊在举步维艰的探索阶段，在发动机设计、制造、试验以及材料工艺方面同欧美国家存在着一定的差距，这导致了目前以歼20、运20和C919为代表的军用民用先进飞机迟迟无法装备“中国心”。在“两机”专项的重大部署和国家科技发展前瞻性布局的支持引导下，与航空发动机相关的诸多工程和基础研究领域的问题已经得到了解决，而进一步深入发掘工程问题背后的基础理论与方法，积极储备面向未来的先进技术，对于中国现有型号的研制和未来型号预研都具有重要意义。

现代先进航空发动机的发展方向不仅是追求更大的推力和更高的效率，大涵道比民用航空发动机也在同时追求更低的排放和噪声，而这些追求的背后也蕴藏了诸多工程和基础研究领域的关键科学问题，不仅包括如何利用气动热力学基本原理实现高性能设计、如何通过模拟燃烧与化学反应动力学过程提高燃烧效率和减少污染物排放、以及如何利用气动声学相关理论降低风扇和喷流噪声等，更是引发了各种亟待解决的复杂流固热声耦合问题，尤其是高推重比与高效率气动设计带来了叶轮机械负荷的增加与流动复杂性的增强，这势必会造成压气机稳定性裕度不足、风扇噪声增强、叶片流致/涡致振动和燃烧室热声振荡等一系列危及发动机稳定工作和飞机飞行安全的工程问题。

作为航空发动机最主要的3大部件，风扇/压气机、燃烧室和涡轮，其各自均对发动机整机性能和可靠性起着决定性的影响。对于压缩部件，高压比、高性能的气动设计的工程应用主要受到稳定性问题的制约。通常，风扇/压气机的工作图谱存在着左侧失稳边界，而发动机稳定工作在共同工作线上，为了避免由于过渡态以及进气畸变等造成工作点偏移越过失稳边界遭遇失速和喘振，工作线与失稳边界需要保持一定的距离，也就是所谓的稳定性裕度。半个多世纪的研究与实践均着眼于如何有效地将失稳边界左移，并在航空发动机压缩系统所需的工作范围内避免失稳现象(失速和喘振)的发生，研究不仅涵盖了其非定常演化的特点，同时也发展了一系列的主/被动稳定性控制方法。早期的关于叶轮机械内部流动失稳问题的各类解析模型也大都关注于失速喘振的起始阶段，从而建立各种各样的特征值问题。然而，为了得到流场扰动的解析解，这些模型中需要做大量的简化和假设。模型的预测精度取决于风扇/压气机损失、落后角和压比等特性曲线的准确性，而这些特性曲线常常又不具有足够的精度，特别是在新的压气机型号设计阶段。大量对经验关系的需求限制了这些模型的应用价值，特别是在实际工程中的应用。因此，发展能够考虑复杂流场及几何条件，不严重依赖经验关系，适用于叶轮机械设计阶段，并且对流动失稳边界可以较为快速准确地给出清晰判据的稳定性模型势在必行，非常富有理论和工程指导意义。

不过即便在设计阶段保留了足够的气动稳定裕度并采取了稳定性控制措施，真实工况下运转的压气机和风扇在部分中低转速时会在近失速区发生叶片颤振，英国帝国理工大学Vahdati教授团队与Rolls-Royce开展了长期的合作，通过复杂的CFD计算探究了这种气弹失稳现象的特性，提出了失速边界在部分中低转速气弹失稳影响下存在“Flutter Bite”现象[1]，二者共同决定了风扇的稳定边界。气动弹性稳定性问题涉及到复杂的气体和固体相互作用，早期学者的研究大多基于解耦假设，因此将气动弹性稳定性问题重点放在求解叶片表面气动力上，进而利用特征值法及能量法对叶片运动稳定性进行判定。由于受到计算能力的限制，先后发展了线性气动力模型、全势流模型、跨声速小扰动模型以及升力面模型等用于叶片表面气动力预测，从而利用特征值方法或者能量法对叶片气动弹性稳定性进行判断。直到20世纪80年代开始利用CFD方法进行流固耦合求解，先后求解Euler方程、RANS方程，但大多数均是弱耦合方法，在此阶段为了降低计算难度，Hall等[2-3]发展了处理叶轮机气动弹性稳定性降阶模型 (Reduced Order Models)，使 CFD 在气动弹性稳定性领域开始占据极其重要的地位。

随着商用航空发动机追求更低污染物排放，军用航空发动机朝向更高推重比目标发展，民用航空发动机环形燃烧室和军用航空发动机加力燃烧室均面临着愈发复杂凸显的燃烧不稳定性问题。燃烧不稳定性问题往往发生在高温高压环境下，涉及燃烧化学反应、湍流流动及复杂环境声学等多时空尺度问题，通过实验和高精度数值方法能够清晰地捕捉局部火焰反应、火焰和流动干涉、火焰对声波响应等局部关键机理信息，但是高成本的实验、高难度的测试、高成本的计算资源决定了不能完全依赖这些方法用于重复性计算的参数优化设计来支撑燃烧室的研制。因此，通过模型方法对燃烧不稳定性发生频率、模态进行准确预测，并发展可靠的控制手段成为了重要研究方向。

诸多物理和工程问题在数学上都归结为求解矩阵的特征值和特征向量的问题，这主要是由于所研究的对象往往都是以动力学微分方程组作为控制方程来描述的，并且由于非线性模型通常可以被近似为线性模型，因此，求解代数微分方程的解析解和数值解就成为了自然科学乃至社会科学问题模型研究的必要手段，相应的研究对象也逐步由代数方程转移到矩阵本身，依靠矩阵相似变换来求矩阵的特征值与特征向量，并以此来反映线性系统的某些物理特征。特征值理论在求解多种稳定性问题上得到了应用，人们在求解诸如Poiseuille流动和Couette流动的稳定性和转捩问题时采用的方法是线性全局稳定性分析方法[4]，假定我们可以精确已知或者估计得到Navier-Stokes方程的定常流动解，如果向这个流动解中引入小扰动，那么线化小扰动方程以及相关的边界条件就是齐次的且与exp(σt)相关，当扰动方程的解存在且Re(σ)>0时，流场就是线化不稳定的。以此为基础，通过小扰动假设和特征值理论，可以研究多种叶轮机领域常见的稳定性问题，因此，本文将简要综述特征值理论在航空发动机流动、气弹和燃烧稳定性预测方面的应用研究现状，并给出笔者所在课题组在相关理论建模的分析与效果验证。

1 基于特征值理论的压气机流动稳定性预测

1.1 线化小扰动稳定性模型

自然界中存在多种流动不稳定性问题，比如与重力和加热相关的稳定性问题、分层流稳定性问题、与离心惯性力有关的稳定性问题、与表面张力有关的稳定性问题、湍流转捩问题。各类稳定性问题由不同的物理机制所支配。研究流动稳定性问题的方法主要分为线性稳定性理论和非线性稳定性理论两种。线性稳定性理论是从无限小扰动的假设出发，流场中的各种变量被分解为平均量和扰动量两部分，并且忽略了小扰动的高阶项，即不考虑扰动之间的相互作用，从而使方程线性化。以线性化方程为基础建立的理论即为线性稳定性理论。线性稳定性理论主要关注的是流体失稳的起始阶段，而不能用来描述失稳后转捩的全过程，因为这个过程主要是非线性效应起决定性作用的阶段。但线性理论可以说明哪种速度剖面在扰动作用下会产生失稳，哪些频率的振动增长最快等，这些对我们预测失稳的发生有着重要意义。而非线性稳定性理论是研究有限振幅扰动波的情况，这时扰动速度与主流平均速度比较起来就不再是很小的量，因此在线化过程中省略掉的扰动量的二阶项不能再被忽略，小扰动方法所计算的结果逐渐偏离实际扰动发展的过程，非线性效应开始显现。按照线性稳定性理论，一旦失稳开始后，扰动应该按照指数关系迅速增长，而实际情况决不可能如此。

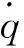
实际上，对于湍流转捩问题而言，流动失稳往往是转捩过程的开始，而并非其全部过程，稳定性理论也不能描述其全过程。然而，目前没有任何一种完整的理论分析能解析地描述转捩的全过程。虽然线性稳定性理论不能用于湍流转捩过程的非线性阶段，但却可以说明哪种速度剖面最不稳定，哪些频率波动增长最快。这和叶轮机械内部的流动失稳问题十分类似，又略有不同。

叶轮机械内部流动的不稳定现象属于流动不稳定性问题中的一种。同时，作为旋转机械，其变工况特征、复杂的几何形状和固壁边界使这一问题更加棘手。迄今为止，叶轮机流动稳定性理论预测研究方法大致可以分为两类：数值计算方法[7-15]和半解析半数值的理论模型方法[16-27]。以Emmons模型[16]和Stenning模型[17]为代表的线化小扰动理论模型、以Greitzer模型[21-22]和Moore-Greitzer (M-G模型[23-24])为代表的系统稳定性模型均是典型的半解析半数值理论模型，其优点在于方法判据清晰、求解快速，适合处理多级压缩系统失速起始判定问题，线化小扰动稳定性模型基于的就是二维不可压小扰动方法，这里不妨展开简要介绍：1955年Emmons[16]采用二维不可压小扰动方法，给出了叶片排出口气流堵塞面积随攻角的变化，建立了压气机失速预测模型，并给出了旋转失速物理现象的经典描述。Nenni和Ludwig[19]建立了能够考虑单排和双排叶栅影响的二维不可压旋转失速稳定性模型，同样给出了稳定性判定的解析表达式，并指出总压损失系数及其导数是影响压气机稳定性的最重要参数。

而系统稳定性模型基于弹簧、质量、阻尼系统类比，Greitzer建立了最初的一维系统稳定性模型，后来Moore和Greitzer将该模型(M-G模型[23-24])推广到二维不可压流，能够进行喘振、失速的稳定性分析。M-G模型采用了大量简化处理，将整个压缩系统作为激盘，无法包含压气机复杂几何造型等因素对稳定性的影响效果，难以适用于具有明显三维特征的旋转失速问题，并且其假设压气机都在静压升系数斜率为零的条件下失稳，用B参数作为判断失稳模式的关键参数，这不是本文重点讨论的内容，因此不再赘述。

采用小扰动方法分析叶轮机流动稳定性问题在很大程度上完全符合研究对象的物理特征，图2给出某单级风扇失速瞬态壁面静压信号空间傅里叶变换幅值曲线[28]，可以看出：扰动波在初始阶段的幅值很小，随后开始逐渐增长直至某一时刻突然非线性放大进入失稳状态。因此，若需要研究失速演化的过程，或者对于某些大尺度扰动(如进口流场畸变引起的流动不稳定性)对流场的影响，可以采用非线性稳定性理论或者数值模拟的方式。然而，如果我们只关注失速起始阶段的系统稳定特性，完全可以采用线性小扰动理论来预测失速的产生。

压气机的流动失稳过程尤其是在失稳起始阶段，通常被认为是扰动演化的开始，此时的扰动幅值较小满足线性假设，通过线性稳定性分析的方式对小扰动的演化趋势进行分析判别可以在一定程度上判断流动的稳定趋势。在稳定性模型发展的早期阶段，经典的线化模型在揭示旋转失速发生机理层面具有重要的意义，但是大量的诸如不可压、无黏、无旋和均匀背景流动等简化假设决定了这些将叶片简化为激盘或者半激盘的集中参数模型无法包含流动非均匀性和叶片力的影响。

为了克服早期经典稳定性模型的这一缺陷，人们开始利用数值线性稳定性分析方法开展失稳预测的尝试，美国麻省理工学院Gordon提出了一个三维不可压数值稳定性模型[25]，在基本流轴对称的假设基础上，用体积力模型替代叶片对流体的作用，包含了子午流面内流动非均匀性。不过，该模型采用的叶片力模型较为粗糙，并且不能包含压缩性的影响，其预测精度和使用范围受到了限制。然而，针对现代高负荷高速压气机而言，发展三维可压缩稳定性模型势在必行。1996年，孙晓峰[26]从三维可压缩线化非定常Euler方程出发，通过与研究流动稳定性所用的三维O-S方程的相应工作类比，采用无穷维系统的截断技术以及有限空间波传播界面间的模态匹配方法，发展了可以考虑任意阶径向扰动的三维可压缩旋转失速稳定性模型。在此工作基础上，本课题组[27-28]结合等价分布源法和传递单元法，将激波匹配关系成功引入半激盘模型中，发展了跨声速风扇/压气机稳定性预测与扩稳理论模型。该模型不关心扰动量的具体数值，因为扰动量的大小是随时间变化的。而失稳是因为扰动量随时间放大所导致，因此该模型只根据扰动量随时间放大还是衰减来判断系统稳定与否。为了更精确地反应流场内的物理画面，使之包含更多的流动细节(尤其是小尺度的扰动)，叶片造型和黏性的影响就要在计算模型中得到考虑，因此求解非定常雷诺平均Navier-Stokes方程的方法开始被引入到压气机稳定性模型中来。

一个动力学系统的稳定性取决于其自身对于系统内部或外部的任何小扰动的响应，而并非针对某一特定的扰动。对于大部分流动稳定性问题而言，扰动总是经历由小到大的发展过程。如果我们更关注流动失稳的开始阶段，那么采用线化处理是可行且合理的。这也就是所谓的理论上任何流动失稳开始问题都可以描述为一个基于Navier-Stokes方程的特征值问题。

该预测方法的有效性在Stage37和NASA两级风扇上得到了验证[28]，Stage37在设计转速下叶尖马赫数为1.4，远远超出了亚声速模型的假定范围，因此，亚模型不适合该转速。即使90%的设计转速下，叶尖部分的大部分流动也是跨声速，只有在70%的设计转速下，叶尖的进口相对马赫数才小于1，因此可以试用文献[27]所发展的模型来预测其失速起始点。

模型预测的结果见图3，图中有两簇曲线，一簇对应延迟时间为0的情况，一簇对应取正常延迟时间的情况；延迟时间在高亚声速压气机中的作用相比低速压气机要明显的多，从图3中可以看出，加上延迟时间后，中性稳定点要略向高流量点偏移，高阶模态下的偏移要大一些；而延迟时间对相对周向传播速度的影响似乎要更明显一些，由此可见，该亚声速稳定性模型在高亚声速条件下也能够做出合乎实际的预测。

NASA两级风扇在第1级转子采用小展弦比设计，目的是消除原有大展弦比风扇叶片的弊端，改善通道流场，提高级压比，减少叶片数目，并用于研究小展弦比叶片的优越性。此外其相对充分的试验数据，也可以用来评估模型对多级压气机稳定性失速先兆点的预测能力。其中，NASA两级风扇失速实验通过在不同的展向位置同时采集径向11处不同点的数据来研究设计转速从50%～100%的失速边界。在完全设计转速情况下，质量流量为33.248 kg/s，总压力比为2.399，绝热效率为0.849(图4)。

图4的结果显示了模型对NASA两级风扇100%设计转速下的稳定性预测。当衰减因子趋于0，压缩机系统的稳定性由稳定状态变为不稳定状态，从而得到失速点，通过分析可以看出理论预测和实验结果之间的误差约5%。

1.2 稳定性预测通用理论

考虑到解析模型和数值模型各自的特点，近年来，一种新的建立稳定性模型的方式得到了发展[29-30]，一方面像解析模型那样，能够为判断失速边界或者失稳点提供清晰的判断依据或准则，同时像数值模型那样，能够包含叶片造型对流场结构的影响，并且不像解析模型那样严重依赖经验关系。这样一种方式，可以提高模型预测的准确性，同时在设计阶段为设计人员提供一种更好的理论预测工具，考虑叶片弯掠、流道结构等复杂造型参数对于稳定性的定量影响，这是以往任何模型所难以比拟的。可以设想，通过应用这样一种在数值解法上可以快速实现、物理层面上可以包含更多因素、失稳点判断清晰明确的模型方法，使其作为稳定性设计而成为压气机设计阶段中的关键一环，而这样一环是当前叶轮机械设计体系中所欠缺的。为了更好地解决风扇/压气机流动稳定性带来的一系列问题，有必要将稳定性设计纳入到现代风扇/压气机设计体系中(图5[29-30])。叶轮机内流通用稳定性模型就是针对这一体系所做的探索实践。

类比层流到滞流的转捩过程问题的处理方法[31-32]，将压气机流场的定常数值计算结果作为某一流动状态的平均流场，并在此基础上引入一个包含所有物理量的小扰动，通过计算将压气机流动作为动力学系统的特征频率来判断其流动稳定性。对于任意的离心或是轴流压气机系统，从最基本的Navier-Stokes方程出发，应用线化小扰动理论，结合浸入式边界方法和体积力方程，发展通用的流动稳定性模型，该模型可以用于任意进出口条件和边界情况下的复杂流动失稳起始点的预测。

该方法的具体操作流程为：从控制方程出发——CFD主流流场——体积力模型——建立特征值问题——求解特征值问题。

根据浸入式边界理论，叶轮机叶片用分布的力源项来代替，从而，叶轮机内部流动由带力源项的Navier-Stokes方程来控制，即：

质量守恒方程：

(1)

式中：ρ为密度；u为速度矢量。

动量守恒方程：

(2)

式中：F为单位质量流量的叶片力矢量；Π为二阶应力张量。

能量守恒方程：

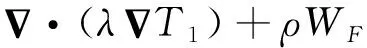
(3)

式中：λ为导热系数；WF表示叶片力做功。

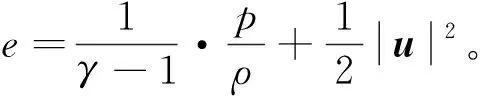
如1.1节所述，发展叶轮机流动通用稳定性理论的核心目的是进行失速起始点的预测，因此，基于小扰动假设，把原始三维非定常流动分解成定常基本流和非定常小扰动之和：

(4)

根据多元函数泰勒展开，叶片力可以线化为

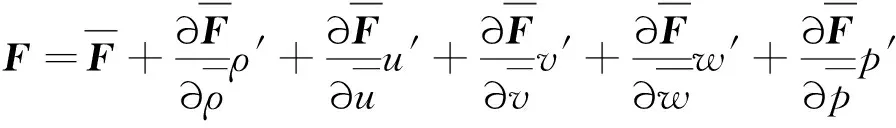
(5)

将式(4)、式(5)代入式(1)～式(3)，减掉基本流所满足的零阶方程并且忽略高阶无穷小量，则可得到线化形式的Navier-Stokes方程。将线化Navier-Stokes方程在圆柱坐标系下展开，可得：

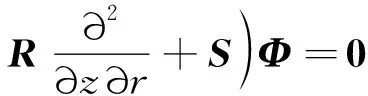
(6)

式中：Φ=[ρ′u′v′w′p′]T，而A、B、C、E、G、H、M、N、Q、R以及S是由基本流所确定的系数矩阵。

一般地，叶轮机内部基本流在径向、周向以及轴向都是非均匀的，假定基本流是定常的，因此，只能对小扰动量作关于时间的正则展开，即：

(7)

将式(7)代入到式(6)，可以得到以复频率ω为特征值的特征值方程：

(8)

根据齐次线性偏微分方程理论，式(8)要有非零解，则必须满足：

det[L(ω)]=0

(9)

通过求解式(9)即可得到复频率ω=ωr+iωi，复频率的实部ωr表征失速先兆波的频率，而复频率的虚部ωi则表征小扰动的演化趋势：ωi为正，则扰动随时间放大，系统不稳定；ωi为负，则扰动随时间衰减，系统稳定。

考虑到叶片力建模以及求解特征方程的复杂性，根据实际工程的要求以及当前的计算能力、设计体系，需要对稳定性理论进行不同层次的简化，得到不同层次的简化模型。当马赫数较低情况下，压缩性对于流动本身影响不大，可以将流动主控方程简化为三维不可压缩Navier-Stokes方程组；对于近似轴对称流动情况，可以重点关注子午平均流面；当径向方向流动可以忽略时，研究二维轴对称流动便能抓住问题的本质和关键；为了进一步简化计算量，准二维流线也可以作为研究主体。这些简化方式要根据实际问题的需要而适当选择，所发展的叶轮机流动稳定性理论模型可被用于轴流压气机和离心压气机的流动稳定性预测，并分析探讨气流压缩性、叶尖间隙及叶片造型对压气机稳定性的影响。

该方法在中国科学院工程热物理研究所的低速轴流压气机实验台和Rotor37稳定性预测上得到了应用验证。图6针对前者低速压气机的计算结果显示：随着压气机截流过程，流量逐渐减小，所有9个模态的衰减因子不断增长。周向传播速度较慢的前5个模态比后4个模态更快地趋于衰减因子临界值。模态1的衰减因子最先由负变正，代表了压气机系统由稳定变为不稳定，因而模态1为最不稳定模态。临界点的质量流量为2.324 kg/s，与实验测得的失稳开始点质量流量的相对误差为0.65%。

Rotor37采用跨声速叶型设计，据了解，目前国际上公开发表的文献中鲜有研究一般压气机结构下跨声速流动失速起始的模型预测。因为在跨声速流场中，叶栅中的激波对流动有重要的影响，使得很难在压气机系统中对其模化。该方法采用周向平均的定常流场分布，叶栅通道内的激波所导致的损失和压升都能包含进入平均流场中，并且经过平均处理后，通道内也不存在流场的跳跃式突变。因此，本模型有可能克服激波这一突跃条件带来的挑战。图7为Rotor37的稳定性预测结果，并在此基础上发展了可以考虑叶片弯掠造型对稳定性影响的预测分析方法。图中：NTD代表无量纲延迟时间。

最近几年，本课题组选择Rotor37为基准叶型，通过沿弦向移动基元叶型来获得一系列的掠叶片，进而采用子午面模型计算预测稳定裕度，并结合定常流场的计算结果，分析讨论气动掠设计对压气机稳定性的影响[33]。

如图8所示[33]，前掠并没有对转子的稳定性造成显著的改变。然而，后掠转子相比Rotor37稳定裕度有明显降低。进一步而言，后掠程度越大，稳定裕度随之单调递减。这一结果与过去的研究定性上是吻合的[34-36]。图中：BS代表Backward Sweep;FS代表Forward Sweep。

以北京航空航天大学单级低速压气机实验台TA36为算例，通过在流线曲率通流设计中调整叶片环量分布设计得到不同负荷分布的转子叶片。采用子午面模型预测其失稳边界，结合定常和非定常流场结果，分析讨论转子叶片轴向负荷分布对压气机稳定性的影响[37]。

对3种负荷分布转子的压气机进行失稳边界预测的结果展示在图9中[37]。可以看到，随着节流过程进行，转子前加载压气机最先失稳，其次为均匀加载压气机，转子后加载压气机最后失稳。这表明，该算例中的转子轴向负荷后移对流动稳定性而言是有利的。

2 基于特征值理论的压气机气弹稳定性预测

航空领域的气动弹性(简称气弹)稳定性问题涉及到复杂的流动和结构相互作用，预测这一问题需要分别对流动以及结构建立相应的模型，然后将二者结合来对气动弹性稳定性进行预测。Theodorsen[38]首次给出了采用特征值理论对气动弹性稳定性进行判断的方法，该方法采用势流理论结合库塔条件描述叶片所受到的流动作用力，同时采用刚体运动方程来描述翼型的振动，联立二者可建立叶片的动力学方程，通过对方程进行特征值分析来判断翼型在特定工况下是否会出现气动弹性稳定性问题。在今天看来，虽然Theodorsen的工作采用了极其简化的模型来描述流动以及结构的动力学特性，但是其采用特征值方法对于气动弹性稳定性进行判断的思想却对随后的研究工作具有深刻的启示意义。

Dowell[39]系统总结了对于单个孤立翼型的特征值分析方法，除了对气动力进行理论建模以外，还可以通过实验数据对气动力进行拟合。Whitehead[40]曾对振荡叶栅的升力系数进行测量以此作为叶片动力学方程中的输入来对其气弹稳定性进行特征值分析。Bendiksen和Friedmann[41]采用特征值方法对一个二维叶栅弯扭复合颤振进行了稳定性分析，Kielb和Kaza[42]通过采用二维梁以及有限元模型来对叶片构建结构模型，结合特征值方法对带掠风扇叶片的颤振稳定性进行了分析，二者对于不可压缩流动的描述均采用Whitehead[40]所给出振荡叶栅气动力模型。Kileb 和Ramsey[43]则采用基于拉普拉斯变换的线化气动力模型对叶栅气动载荷进行建模，通过特征值方法给出对超声速流动下叶栅的气弹稳定性变化趋势。

在早期计算能力不发达的年代，进行特征值分析的前提是需要将气动作用力解析表达成频域形式，而对于压气机内的相关问题，叶片气动载荷的建模多取自于外流孤立翼型中相关的研究结果，这也导致理论结果与真实现象存在较大的出入[44]。压气机叶片由合金制造，质量比较大，此时颤振通常表现为单一的模态，而外流机翼中多为复合模态；另一方面，压气机内部的流动受到叶片和流道复杂几何、固壁以及上下游结构的影响，其复杂程度远高于外流问题，并且表现出明显的流固耦合特性，对叶片气动作用力进行准确的理论建模难度较大，因此适用于外流气弹分析的理论解耦模型通常难以准确描述压气机内部的真实流动情况。虽然部分基于解析方法的预测模型被用于设计阶段的快速迭代，但是通常认为这一类方法预测的结果与实际问题有着较大差别。

Carta[45]提出了一种能量法的判据来预测压气机叶片是否会出现颤振问题，这一方法所采用的气动力及叶片结构模型与Theodorsen的工作是类似的，但是区别在于Carta并没有对控制方程的特征值进行求解，而是只提取了结构方程部分的特征频率，在此基础上假设叶片在特征频率处做简谐运动，这一做法与Whitehead[46-47]的工作中对流体域与固体域做解耦处理是一致的，通过计算一个周期内气动作用力对叶片所做的功来判断叶片与流动之间的能量传递情况，即气动阻尼功，如果气动力对叶片输入负功，则认为流动对叶片的振动起到阻尼作用，此时叶片处于稳定状态，否则即可能发生颤振。这一基于能量法的颤振判断准则在压气机的气动弹性问题预测中一直沿用至今。

2.1 基于能量法的快速气弹预测算法

能量法通过指定叶片振动规律来对气弹问题进行解耦，其核心问题在于如何对流动的非定常响应进行预测。在压气机设计阶段，对于预测方法的主要要求便是能够实现高效迭代以完成快速设计，此时流场对于叶片非定常输入的响应多采用简化的解析方法来建模。Sun等[48]采用三维升力面理论来求解由叶片振动诱导产生的非定常载荷响应：在叶片表面建立无穿透边界条件，要求来流扰动速度场与叶片振动速度在叶片表面法向和速度为零，通过将速度脉动转化为压力脉动的积分方程，如图10所示，结合广义声类比积分公式，可将转子散射的压力脉动场写为

(10)

假设压力脉动存在时空周期性，则叶片上下表面压差可展开成傅里叶级数的形式：

(11)

进一步结合格林函数，散射的压力脉动场可写为积分方程的形式：

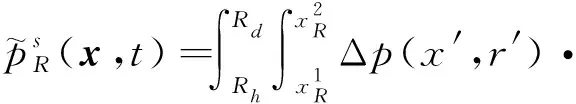
(12)

近年来，部分研究结果表明转子进口段的长度以及声处理可能会对转子的颤振稳定性产生较大的影响[48-49]，为了考虑进口段长度以及声衬边界条件的影响，Sun等[48]结合传递单元方法，通过等价分布源方法来描述声学边界对于叶片颤振的非定常响应，同时采用边界元方法来刻画管道边界的反射效应，成功建立了有限/无限长管道内的流固声耦合的预测模型。

图11给出了不同声学边界条件下转子叶片气动功Waero的变化结果，叶片振动呈现为一阶弯扭复合模态，当振动节径ND=2时，气动功的刚壁值小于0，即转子在刚壁管道中是稳定的，而当阻抗为Zs=(0.05,-3.9)的声衬被加入管道后，气动功进一步下降为一个绝对值比原刚壁值大两倍的负数，这也意味着气流对转子的阻尼效应增强。而在同一条件下，若声衬阻抗为Zs=(0.05,-3.2)，则声衬反而会对振荡转子的气动弹性响应产生负面影响，触发叶片产生颤振。这一对比说明，壁面声处理对于转子颤振稳定性产生重要的影响。

与此同时，转子进口管道的长度也可能对振荡转子的气动阻尼产生重要的影响，图12给出了不同管道长度下，进口距叶片前缘面距离长度对于振荡转子气动功的影响结果。图中：FLD和LID分别表示有限长和无限长；Lduct为管道长度；Ca为叶片轴向弦长。从图中可以看到，基于有限长和无限长管道模型所得到的非定常气动功存在明显差异。当管道总长度为5倍叶片轴向弦长时，如图12(a)所示，非定常气动功会随着进口段长度增加而由负值逐渐变为正，这也意味着进口段过长可能导致转子出现颤振。而在图12(b)所给出的管道长度为15倍叶片轴向弦长的情形下，当转子位于管道中间位置时，非定常气动功的数值最小，此时转子叶片最稳定，而当转子逐渐靠近进口或者出口位置时，非定常气动功的数值呈现出逐渐增大的趋势直至变为正，这也意味着对于图中所考虑的振动模态，转子过于靠近管道进口或者出口可能导致颤振的发生。

2.2 气流非定常载荷预测方法

近年来，随着计算方法以及软硬件的发展，基于CFD方法求解更为复杂的非线性流动模型在气流非定常载荷的预测中扮演着越来越重要的角色。在20世纪80～90年代，受制于计算能力的限制，Hall和Crawley[50]通过对非线性欧拉方程进行线化的方式来提升计算效率。线化后的欧拉方程可以在特征频率处做周期性假设，对于气弹问题，这一频率通常是叶片的振动频率，进而可以求得该特征频率所对应的空间特征向量，特征向量的物理意义是周期性的流动在空间各处脉动的幅值。计算效率是评估压气机气弹预测方法的核心指标之一，而基于特征频率的处理手段可以避免对时间项进行迭代求解，因而可以大幅提升计算效率。当流场中不存在强非线性结构时，比如流动分离以及激波，基于线化方程的计算方法能够对由叶片振动引起的非定常现象进行合理的预测，而当流场中非线性作用占据主导时，频域线化方法则不再适用。

为了进一步考虑包含非线性的影响同时兼顾频域方法在计算效率上的优势，He和Ning[51]提出了一种非线性谐波方法，这一方法的核心思想是在对Navier-Stokes方程进行线化的过程中保留扰动交叉项，以特征频率对扰动进行周期性假设，在对扰动求解的过程中同时对包含非线性因素的时均流场进行同步修正直至结果收敛。相较于非线性时间推进，非线性谐波方法的计算效率仍然有1～2个数量级的提升。基于类似的思想，Hall等[52]提出了一种求解具有时空周期性非线性流场的谐波平衡方法，这一方法通过迭代求解特征频率及其各阶谐波所对应的空间特征分布来对流场进行时空重构，能够实现较高的非定常计算效率。非线性谐波法以及谐波平衡方法是目前研究压气机叶片气弹问题的主要模拟工具。Clark[53]采用谐波平衡方法对压气机叶片的流动进行快速模拟，在此基础上采用POD(Proper Orthogonal Decomposition)方法提取流场中的主要模态来构建降阶模型并尝试将其应用于转子非同步振动问题的预测。Wang和Huang[54]提出了一种针对谐波平衡方法的加速收敛方法并将其应用在跨声速转子的气弹稳定性预测。Huang等[55]采用谐波平衡方法结合影响系数法求解了叶片振动模态处的气动作用力，在此基础上结合仅包含指定模态的结构动力学方程对叶片的颤振实现基于小扰动的特征值分析。基于谐波平衡的思想，Du和Ning[56]提出一种采用多项式来简化时间项的方式，同样能够准确地对具有时空周期性的流动进行预测。Sandberg和Michelassi[57]与Casoni和Benini[58]针对轴流叶轮机械领域典型的数值模型以及频域和其他各类降阶模型给出了全面的总结。

2.3 耦合计算的应用场景

采用时空周期性假设的求解方法一般要利用特征频率对时间项做傅里叶展开，而当流场中同时包含多个特征频率时，如多叶片排干涉上下游叶片通过频率不同，以及转静干涉的同时还存在叶片振动，这一类方法通常只能对不同频率做线性叠加而无法考虑彼此之间的非线性耦合效应。当不同频率线性叠加，多个频率互相靠近产生“拍”现象时，计算收敛时间也会大幅延长[59]。这一类方法实际上是解耦的，即没有考虑流场演化对于叶片振动频率、振幅以及叶片间相角的影响。由于目前复合材料的大量应用，叶片质量相较于早期已经大幅降低，此时叶片振动频率及模态与不考虑流固耦合效应的结果会存在差异，与此同时，叶片振动响应可能包含多个模态，采用频率解耦方法不符合真实的物理演化过程。Chahine等[60]的计算结果表明，随着质量比以及结构刚性的降低，耦合效应的作用越来越显著，由此导致耦合方法与解耦的能量法所给出的结果差异越来越大。在流固耦合效应起主导作用时，基于全非线性方程的耦合计算则显得十分必要[61-62]。

另一类必须采用耦合模型计算的振动问题是转子非同步振动问题。近年来国外研究机构在不同的实验平台上都曾测量到了叶片非同步振动的信号[63-65]，这一现象一般呈现出高周向模态数，并且伴随着沿周向传播的分离流动结构，同时壁面压力信号存在多个非轴频整数倍的异常成分。Sun[48]和Vahdati[49]等的工作都表明，进口管道的反射会对转子风扇的非同步振动稳定性产生明显的影响。对于这一现象必须采用耦合处理的原因在于，从实验结果来看，受到叶片振动与流动之间干涉效应的影响，流动的周向模态特性在振动前后会出现明显的改变[64-65]，即流固耦合效应在这一现象中同样扮演着重要的角色。目前针对非同步振动问题已有较多的研究结果，在判断叶片非同步振动的稳定性时，绝大多数工作[66-69]仍然采用解耦的处理方式，即给定频率和振幅并且使用气动阻尼这一参数。气动阻尼这一概念源于线性范畴，需要参照给定的叶片振幅做无量纲从而保证气动阻尼与振幅无关而非同步振动往往伴随着沿周向传播的分离流动，表现出强非线性特征，在此情形下，振幅对于气动阻尼计算结果的影响目前尚不明确。虽然叶片的振动频率可能仍然是固有频率，但是非同步振动的周向模态特性与流动密切相关，同样无法在计算前获得，并且叶片的振动会显著改变流动的周向模态特性，这也意味着无法准确地给出周期性边界条件，因此大多数情况下需要开展全环计算。较于上述基于频域假设的快速非定常求解算法，采用时间推进方式求解完全非线性的Navier-Stokes方程能够包含更多复杂流动因素，因此也被广泛应用于压气机气弹问题预测，同时其对于计算量的要求也进一步提升。

3 基于特征值理论的燃烧不稳定性预测

燃烧不稳定性的发生是燃烧系统内火焰非定常热释放和声波的充分耦合导致的[70]。因此，燃烧不稳定性的发生关键在于火焰非定常热释放和声波的耦合，将复杂问题降阶简化，保留影响燃烧稳定性发生的关键因素，即火焰对声波的响应，以及影响声波反射的燃烧室的阻抗壁面刻画，在其他部分忽略次要因素，比如整个燃烧室内复杂的湍流流动、燃烧反应等，而只考虑声波传播[71]。通过模型实验和高精度数值模拟可以得到火焰对声波的响应，在线性频率内得到火焰传递函数(Flame Transfer Function, FTF)[72]，在非线性频域范围内，Dowling等发现燃烧不稳定性非线性的主要因素在于火焰对不同幅值声波响应的不同，因此可以通过建立包含声波幅值影响的火焰函数，也称火焰描述函数(Flame Describing Function)[73-74]用于非线性燃烧不稳性分析。至于燃烧室其他部分则通过建立声学模型，结合火焰传递函数在不同界面上进行守恒方程匹配。

燃烧不稳定性分析本质上是基于小扰动特征值理论的稳定性分析，即分析燃烧系统有燃油当量比脉动、旋涡脱落及燃烧噪声等小扰动存在的情况下，系统的响应特征，如果在施加起始小扰动后的一段时间内，系统的脉动幅值不断放大，则表明燃烧系统是线性不稳定的，反之，则是线性稳定的。基于这样的认识，我们可以对系统控制方程进行线化处理，得到关于小扰动量的控制方程，并求解其复特征频率，其中复特征频率的实部表示系统的热声共振频率，虚部则代表系统不稳定性的增长率，通过这种理论模型方法，可以快速进行燃烧不稳定性的预测或研究控制手段[75-76]。

国际上通用的声网络低阶模型方法在认识燃烧不稳定性发生机理及对燃烧室进行稳定性预测方面发挥了重要作用，能够为燃烧不稳定性控制提供准确的目标，不稳定模态及频率。在考虑控制手段设计时，以上模型方法能够直接在特征频率分析中考虑具有集总参数特点的Helmholtz共振器[77-78]。但是，当需要对燃烧室中常常使用的兼具冷却壁面和提供声学耗散作用的含冷却偏流穿孔板声衬[79]等具有分布参数特点的控制壁面设计时，需要配合额外声学计算[80]或实验[81]。但是这种根据频率、模态信息再通过声学计算或实验解耦地设计燃烧不稳定性抑制手段往往会带来误差。这是因为，首先，穿孔板声衬等声学软壁面在燃烧室内会改变系统的热声共振频率和模态分布，因此，在硬壁面条件下建立的预测模型不能准确预测带有声衬的燃烧室共振频率和模态分布。另外，通过声学计算或实验设计声衬过程中，声衬面临的声学环境也很难完全实现其在燃烧室内的环境。因此，为了研究声衬控制热声不稳定性效果，并准确地对声衬参数进行优化设计，建立一种能够将声衬耦合考虑的燃烧不稳定性模型就显得十分重要而且必要了。

3.1 耦合考虑声衬壁面的三维燃烧不稳定性预测模型

将声衬耦合考虑进燃烧不稳定性模型中，难点在于如何描述燃烧室内声波和壁面的相互干涉作用。在软壁面环境下，壁面阻抗、系统频率、管道特征值形成复杂的耦合迭代关系[82]。为了解决这一难题，Sun等提出一种基于等价分布源思想[83]的传递单元方法[84]，将声衬穿孔板阻抗边界视为等效连续分布的单极子声源，这样能够保留管道特征值的正交特性，避免软壁面管道径向特征值的复杂迭代求解。传递单元方法，可以用以考虑有限长声衬的声传播问题，也可以用以将声衬作为声学传递单元包含到燃烧不稳定性模型。

该方法在处理声衬段声学单元时，为了可以将之耦合到燃烧不稳定性分析模型中，需要得到其传递矩阵，即声衬段内声波关于界面入射波的显示表达式。具体地，将声衬软壁面视为等价连续分布的单极子声源，声衬段的内压力扰动和速度扰动表达式可以写为界面入射声波和散射声波之和：

p′=p′I+p′d

(13)

其中：

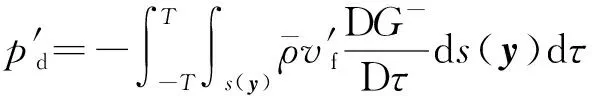
(14)

声衬背腔管道内由声衬单极子声源产生的散射声场为

(15)

p′c-p′=Zv′n

(16)

式中：Z为穿孔板声阻抗；v′n为垂直于声衬表面的声质点速度。通过阻抗方程以及声衬前后端界面匹配条件即可求解得到等阶声质点速度的表达式，再将之代入方程(13)和方程(14)即可以得到声衬段内声场关于界面入射波的显示表达式，即完成了声衬段声传递单元的建立详细推导过程和表达式参考文献[84]接着可以和燃烧室内其他硬壁面条件下声网络单元建立起燃烧不稳定性分析模型。关于模型建立的细节可以参考文献[85]。应用该特征值分析模型，可以研究不同形式的声软壁面控制对燃烧不稳定性的影响，并进行快速的参数优化设计。

从Rayleigh准则出发可知，控制燃烧不稳定性的发生可以从两个方面着手，一是削弱热声耦合强度[86]；二是增加系统的声学耗散[82,85]。下文将从增加系统声学耗散角度研究穿孔板声衬在环形燃烧室中控制热声不稳定性来阐述本三维模型方法的应用。

3.2 穿孔板声衬控制环形燃烧室热声不稳定性

环形燃烧室由于其能产生更均匀的燃烧，具有结构更紧凑的优点，目前是航空发动机和地面燃气轮机领域最为常用的燃烧室类型。为了满足日益严苛的排放标准，环形燃烧室多采用贫油预混燃烧，具有较低的NOx(氮氧化物)排放，但更易出现燃烧不稳定性。此外，由于燃烧温度较高，燃烧室火焰筒壁面往往开有小孔，从高压压气机后引入部分冷气从小孔内通过，形成小孔冷却偏流，自然形成了具有声学耗散的穿孔板声衬结构。穿孔板声衬在满足冷却需求的情况下，还能提供声学耗散在线性范围内抑制燃烧不稳定性的发生，或尽可能的降低振荡幅值。目前，由于巨大的计算资源和时间成本，还难以通过数值模拟如大涡模拟(LES)研究不同声衬结构的控制效果。而采用本文所介绍的包含软壁面声衬的燃烧不稳定性模型则可以进行声衬控制效果的研究以及参数的优化。

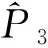
通过与有限元分析软件COMSOL对比无热释放条件下系统的特征频率及模态分布情况，验证本模型的有效性，频率对比如图14所示。图中模态名称中，L表示轴向模态，A表示周向模态，字母前数字表示模态阶数，如2L0A代表第2阶轴向模态混合0阶周向模态。从图中计算结果还可以发现，声衬的引入使得必须考虑径向耦合模态，才能准确预测频率以及模态分布。也就是说，当我们考虑包含声软壁面的燃烧不稳性预测时，有必要发展三维模型，才能够准确预测系统的频率及增长率。

为了研究声衬控制效果背后机理，给出系统内声压分布，对于模态2L0A声衬控制效果最好的声衬位置大小L2/Lc=0，L3/Lc=0.47，系统内声压分布如图15(a)和图15(b)所示。图中：

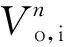
以上研究结果表明，对于包含声衬的燃烧室系统，有必要建立三维燃烧不稳定性模型通过特征值分析理论，预测系统的稳定性并研究声衬的控制效果。声衬的大小和位置对于其控制燃烧不稳定性效果有重要影响，可以通过改变声衬背腔结构提高声衬的控制效果。另外，值得一提的是，在实际系统中，由于火焰的非线性，还可以通过本模型方法结合非线性火焰函数模型[88]，以研究不同声衬结构对降低热声不稳定性极限环幅值的影响，以满足工程实际需求。

4 总结与展望

随着航空发动机设计理论和三维数值模拟技术的不断发展，针对发动机内流、气弹和燃烧领域面临的工程技术问题，各种理论模型和实验数据库也更加完善，设计人员普遍习惯于通过所积累的设计经验来预估和判断风扇/压气机以及主燃/加力燃烧室的稳定工作范围，但基于经验的评估方法很难被纳入到一体化设计工具中并对设计方向给予合理的引导，因此，快速准确的稳定性评估工具对于航空发动机的设计至关重要。本文简要阐述了基于小扰动方法的特征值理论在航空发动机气动、气弹和燃烧稳定性预测方面的应用，对从经典的线化小扰动模型到发展较为成熟的半解析模型方法的研究发展进行了综述，并重点以本课题组近年来的研究结果为例，给出了该方法在流动失稳预测、叶轮机设计和燃烧不稳定性预测方面的应用案例。实践表明，该方法可以作为发动机一体化设计分析工具成为发动机稳定性设计过程中的一环。

此外，鉴于壁面边界条件可以影响小扰动在动力学系统内的演化行为，在本文所介绍的理论模型基础上，相继有通过壁面阻抗调控方法控制流动失稳和热声不稳定性的技术手段被发展，为失速喘振和燃烧不稳定性的控制提供了新的实现手段。面向未来更先进航空发动机研制的需求，基于特征值理论的稳定性模型方法需要考虑更加复杂的壁面边界条件、几何影响因素、更多非定常扰动干涉机制，以及非线性因素等，以快速低成本的方法优势支撑行业发展可靠、高效的稳定性评估工具。