真空羽流智能化计算

蔡国飙，张百一，贺碧蛟，翁惠焱，刘立辉

1. 北京航空航天大学 宇航学院, 北京 100191 2. 航天器设计优化与动态模拟教育部重点实验室, 北京 100191

卫星、飞船、空间站和地外天体探测器等航天器在太空中采用姿轨控发动机实现位置保持、姿态控制和轨道转移等。真空环境中，发动机喷流向外部环境自由膨胀形成羽毛状流场，称为真空羽流[1]。真空羽流会对航天器产生气动力、气动热、污染、电磁干扰和视场干扰等效应，统称为羽流效应[1]。羽流效应会干扰航天器正常工作状态，甚至影响航天器寿命和任务成败。因此，真空羽流及其效应评估和防护是航天领域的重要科学和工程问题。真空羽流包括连续介质流、过渡区域流和自由分子流等全流域状态，流动机理极其复杂。常用的真空羽流及其效应研究方法包括理论研究[2]、在轨实验[3]、地面实验[4-5]和数值模拟[1,6-7]等。北京航空航天大学研制了基于液氦/液氮组合双层一体深冷泵的真空羽流效应实验系统[8]，开发了具有自主知识产权的、基于直接模拟蒙特卡洛方法(DSMC)[9-11]的通用并行仿真软件羽流工作站(Plume Work Station, PWS)[1,6-7]，建立了航天器全状态羽流效应实验仿真耦合评估体系。研究成果已成功应用于长征、神舟、天宫、嫦娥和天问等系列航天器。

真空羽流控制方程为Boltzmann方程，理论研究非常困难；在轨实验风险大，且费效比巨大；地面实验常受限于真空舱尺寸和动态真空度而无法进行全尺寸发动机羽流及其效应研究。因此，数值模拟是当前航天领域应用最广泛的研究方法。DSMC方法是稀薄流领域中较为成熟且精度最高的数值模拟方法，但DSMC方法本质上是基于第一性原理的粒子模拟，需要同时跟踪大量模拟粒子的运动，非常耗时[12]。如月球探测器着陆月面过程中，数值模拟全尺度(～30 m)发动机羽流及其与月壤作用过程，DSMC计算的时间可达数天甚至几周，严重影响工程设计部分的迭代设计进度。此外，中国正在开展载人登月关键技术攻关，真空羽流与月壤相互作用评估及控制是其中一项关键技术。真空羽流与月面作用会激起月尘[6,12]，引发仪器读数错误[13]和视野遮挡[14]等问题，因此实时预测羽流场及月尘可为保障航天员/航天器安全及任务成功提供关键数据支撑；但受限于计算效率，DSMC方法无法实现实时预测。由此可见，大幅提高真空羽流数值模拟效率十分必要。

近年来，人工智能[15]和深度学习[16]的发展为科学家和工程师们提供了新的技术手段，相关技术已广泛应用于计算机视觉[17]，自然语言处理[18]、语音识别[19]以及航空航天领域的相关问题[20-27]。研究发现[28-35]，深度学习技术可在连续流领域实现快速计算。Sekar等[28]使用卷积神经网络(CNN)和多层感知机(MLP)预测了不同几何结构机翼的升力系数：首先使用CNN由多种机翼构型抽象出16个几何和气动参数，然后将这些参数输入MLP网络预测升力系数。结果表明，升力系数预测精度可达97%，并且计算速度相比传统的计算流体力学(CFD)方法快了约150倍。Hui等[29]同时使用前馈神经网络和CNN计算了机翼附近的压力分布。研究中机翼的几何形状被抽象为符号距离函数，并和CFD方法计算出的机翼附近的压力分布数据共同输入神经网络进行训练，以此预测压力分布；结果显示预测的均方根误差在2%左右，并且其计算速度相比CFD方法提升了约3个量级。Wu等[30]使用数据驱动的方法，提出了一种数据增强的生成对抗神经网络(GAN)，用于机翼层流压力分布的快速精确预测。该计算方法分为流场预训练模块和微调模块，预训练模块使用条件GAN估计训练集的分布；微调模块用于增强模型的泛化性能。结果显示上述方法可以准确计算机翼附近的流场和压力系数。总而言之，深度学习技术已成功应用于连续流领域，且其计算效率显著优于传统CFD方法，为提高稀薄流领域的计算效率提供了可能，但当前尚未开展针对真空羽流快速计算的研究。

本文提出了一种基于卷积神经网络的直接模拟蒙特卡洛方法(Convolutional Neural Networks-based Direct Simulation Monte Carlo method, CNN-DSMC)，实现了月面探测器月面着陆过程中真空羽流的快速计算。该方法使用卷积神经网络从DSMC数值模拟结果中提取特征，以此训练真空羽流智能计算模型，然后将DSMC数值模拟中不同的几何拓扑和边界条件输入计算模型完成真空羽流场智能化求解。结果表明，和传统的DSMC方法相比，CNN-DSMC方法可以在保持较高计算精度的同时显著降低计算时间，大幅提高了真空羽流评估效率。

1 理论方法

本文以月面探测器月面着陆过程中真空羽流流程为例，分别通过基于卷积神经网络的直接模拟蒙特卡洛方法(CNN-DSMC)和DSMC方法模拟月面探测器在不同悬停高度时的真空羽流流场。本节主要阐述CNN-DSMC和DSMC方法。

1.1 基于卷积神经网络的直接模拟蒙特卡洛方法

图1为CNN-DSMC方法求解流程示意图。在CNN-DSMC方法中，计算分为数据预处理和模型训练2个过程。在数据预处理中，真空羽流仿真模型中的几何拓扑信息被抽象为符号距离函数(Signed Distance Function, SDF)，边界条件信息被抽象为标识符矩阵(Identifier Matrix, IM)；SDF和IM共同作为训练集的输入；将由DSMC数值模拟得到的真空羽流速度场(3个)和密度场作为训练集的输出；测试集为未参与训练的DSMC数值模拟算例，用于验证CNN-DSMC方法的准确性。在完成训练之后，就得到了真空羽流智能计算模型：

(V,ρ)=f(D,M)

(1)

式中：V和ρ分别为真空羽流速度矢量和密度；D和M分别代表符号距离函数和标识符矩阵。接下来分别对CNN-DSMC方法中的真空羽流仿真模型、卷积神经网络和数据预处理方法进行介绍。

1.2 真空羽流数值模拟模型

本文中DSMC算例均是通过北京航空航天大学羽流工作站PWS[6-7]完成的。PWS软件中航天器面网格和DSMC计算的体网格是解耦的，并且采用了自适应网格加密策略，方便计算各种复杂工况。此外，PWS软件可以进行多核并行计算，且实现了真空羽流热效应分析[5]、力效应分析[36-37]和污染效应分析[38-39]等方面的数值模拟。地面实验结果表明，PWS软件数值模拟结果与实验符合较好，可以满足本文数据的精度要求，详见附录A。

本文研究的月面着陆过程羽流仿真所采用的计算域如图2(a)所示。除了月面，计算域的其余5个边界均设置为开放边界。月面和月球探测器表面设置为固体边界，热适应系数设置为1.0[40]。所有边界的温度设置为300 K，粒子与边界相互作用模型使用Maxwell模型[41]。DSMC数值模拟的时间步长设置为10-7s。

定义月球探测器足垫到月面的距离为h，且以h= 10 m为界限区分羽流智能计算的近场模型和远场模型。当h≤ 10 m时，羽流流场中的激波相互作用非常复杂，流场形态比远场情况更加混乱。因此，在近场情况下，由于计算域范围较小且流场更为复杂，应用CNN-DSMC方法对全局羽流流场进行训练；在远场情况下，由于流场结构更简单，且计算域范围较大，因此截取月面上方6 m处的流场用于CNN-DSMC训练，如图2(b)所示。近场和远场的训练集与测试集设置如表1所示。训练集和测试集选取依据详见附录B。

表1 训练集和测试集设置Table 1 Configurations of training and test datasets

1.3 卷积神经网络

CNN-DSMC方法中使用的整体网络结构如图3(a)所示。该网络由1个编码器和2个解码器组成，其中每个编码器(解码器)都由7个(反)卷积块组成。每个(反)卷积块的结构组成包括3个(反)卷积层和1个最大(反)池化层，如图3(b)所示。单个(反)卷积层包括(反)卷积、激活函数和批量正则化3个过程。卷积本质上是一种矩阵变换，对于给定的矩阵A，卷积操作定义为[42]

B=wA

(2)

式中：B为卷积后得到的矩阵；w为卷积核，也是一个矩阵，其矩阵元素将在神经网络训练中不断进行优化。反卷积则是上述计算的逆过程。文中使用的激活函数为Relu[43]，其定义为

Relu=max(0,x)

(3)

式中：x为(反)卷积的输出矩阵。批量正则化[44]主要用于修正每一层输入数据的期望和方差，有利于训练过程的效率与稳定性。最大池化层的作用本质上是下采样，而最大反池化层用于上采样。

除了前馈过程，编码器中每个卷积块的输出都会输入解码器中对应位置的反卷积块，该设置参考了ResNet[17]，是训练中避免梯度消失和梯度爆炸的关键操作。表2给出了CNN-DSMC方法中的参数设置，其中的参数是大量数值实验后得到的较优数值。卷积层结构{8, 16, 32, 32, 64, 64, 128}对应7个卷积块，对于反卷积块，上述结构反序。卷积核大小为5，即卷积核矩阵的形状为5×5×5。在训练过程中，使用的优化方法为AdamW[45]，其存在权重衰减功能，有助于提高训练过程的稳定性。训练中使用的损失函数为真空羽流速度场和密度场的均方根误差，表达式为

表2 CNN-DSMC方法中的参数设置Table 2 Parameter setting in CNN-DSMC

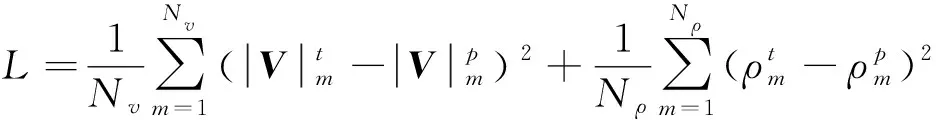
(4)

1.4 数据预处理

在CNN-DSMC方法中，真空羽流仿真模型中的几何拓扑信息被抽象为SDF[24,46-47]。定义Ω为度量空间Y的一个子空间，度量空间Y代表了DSMC羽流数值模型的几何拓扑信息，其本质是一个矩阵，该矩阵元素的值仅包括-1和1两种情况，在航天器内部为-1，航天器外部为1。SDF被定义为[48]

(5)

式中：d为欧几里得距离；∂Ω为Ω的边界；Ωc为Ω的内部。对于任意y∈Y，有

(6)

式中：inf代表下确界。SDF的物理意义为空间中的某个点到边界的最小距离，其符号由该点是否在边界内决定。式(5)中的D可以通过快速行进算法[48-49]得到。本文中输入CNN-DSMC网络的SDF在基于式(5)的情况下还进行了归一化处理，如图4(a)所示，月球探测器内部区域的SDF为负值，月球探测器外部的SDF为正值，且值的大小随着接近月球探测器边界而减小。

在CNN-DSMC中，边界条件信息被抽象为IM。IM本质上是一个三维的矩阵，其矩阵元素作为区分三维空间不同区域的标识符。在本文中，共选取4种不同的标识符：开放边界、航天器边界、月面边界和真空羽流区域，这4种标识符也与实际DSMC数值模拟中使用的边界条件相对应，如图4(b)所示。在具体设置中，除了月面，最外面的5个边界的标识符均设置为开放边界；航天器表面及内部设置为航天器边界；月面设置为月面边界；真空羽流流场设置为真空羽流区域。

远场情况下，由于流场区域很大，所以只截取了月面上6 m作为训练区域(图2(b))。在此种情况下，输入CNN-DSMC中的信息额外包括了所截区域第1层网格的流场(速度、密度)信息，信息从h=30 m的算例中截取。

2 结果与讨论

通过DSMC数值模拟获得落月过程中远场和近场的真空羽流流场数据，将其输入CNN-DSMC网络中进行训练，共训练40 000步，分别得到的远场和近场流场训练过程中的损失函数曲线如图5所示。结果表明，训练过程中，近场的损失函数下降更慢，且最终达到稳定的值(约为10)也比远场的值要大；远场的损失函数最终稳定在0.1附近。尽管远场的实际区域大于近场，但远场用于训练的区域高度仅有6 m,小于近场的训练区域高度10 m,且近场流态复杂，训练出的计算模型精度要低于远场情况的模型，因而远场训练损失函数的稳定值更小。接下来将分别展示远场和近场的结果对比。

2.1 远场(h > 10 m)结果分析

图6为远场验证算例(h=18 m)真空羽流速度场的DSMC数值模拟结果和CNN-DSMC计算结果的三维切片。图中的u代表真空羽流在x

方向的分速度。由于远场情况只截取了月面上方6 m处的流场(图2(b))用于CNN-DSMC训练，在截取区域上方，两者的流场是完全相同的，所以图6只给出了这一局部范围流场的对比。从图中可以看出，整体上两者得到的流场是非常相似的，而且流场计算结果表明CNN-DSMC可以正确地计算激波以及多条激波相互作用后的复杂流场。

利用CNN-DSMC还能同时得到真空羽流密度场，图7给出了月面上方0.1 m处的密度分布。相比于速度场的结果，密度场的CNN-DSMC计算结果与DSMC数值模拟结果的一致性稍差一些，但是不一致的区域基本都位于非核心流域(>10 m)，这些区域的密度相比核心区的密度低了4～5倍，体现为式(4)中的损失函数密度项权重更小，因此计算误差会稍大一些。

为了定量分析CNN-DSMC计算结果和DSMC数值模拟结果之间的差距，截取了月球探测器轴线(y=0 m,z=0 m)上的真空羽流速度和密度数据，如图8所示。图8(a)和图8(b)分别为x方向速度u和密度随距离的变化曲线，需要说明的是，给出的曲线在x方向的范围为-10～-4 m，对应于所截取的月面上方6 m的真空羽流流场；其中，-10 m对应于月面的位置，-4 m对应于截取平面的位置。图8所示结果显示CNN-DSMC计算结果与DSMC数值模拟结果几乎相符，特别是激波附近处的结果也相符。

计算结果表明，CNN-DSMC计算和DSMC数值模拟得到的速度和密度的平均相对误差分别为4.1%和8.2%。进一步计算相对误差发现，流场速度和密度在核心区域的最大误差分别为3.2%和9.9%，但在激波附近的最大误差会增加到14.9%和28.9%。受限于DSMC计算时间，本文远场条件下的训练集只包含6个算例(见表1)，因此CNN-DSMC计算结果局部偏差较大；但从图8所示结果仍能看到CNN-DSMC方法的可行性。

2.2 近场(h ≤ 10 m)结果分析

图9为近场验证算例(h=8.2 m)真空羽流速度场的DSMC数值模拟结果和CNN-DSMC计算结果的对比。与图6不同，由于近场情况使用全局真空羽流流场数据进行训练，因此图9展示的结果为全局的流场结果。可以看出，两者得到的速度场几乎完全一致，CNN-DSMC计算的激波形状也与DSMC数值模拟结果一致。同时，考虑到真空羽流近场结构的复杂性，图9还给出了流线的分布，结果表明DSMC数值模拟结果和CNN-DSMC计算的粒子运动轨迹也基本相同。

图10所示为月面上方0.1 m处的真空羽流密度分布。与图7展示的结果不同，近场情况下的CNN-DSMC计算出的密度分布和DSMC数值模拟结果差别更小，这是因为近场情况下的整体羽流密度(10-4)比远场情况(10-5)高了一个量级，使得式(4)中的损失函数密度项权重更大。

图11(a)和图11(b)分别近场情况下月球探测器x方向速度和密度的变化曲线，范围为-9～-1 m，其中：-9 m对应于月面位置，-1 m对应于月球探测器正下方与足垫同一高度的位置。结果表明，和远场情况类似，CNN-DSMC计算得到的速度和密度与DSMC数值模拟结果基本一致；其平均相对误差分别为6.0%和8.8%，在核心区的最大误差分别为1.3%和4.5%，在激波附近的最大误差分别为10.9%和14.6%。相比于远场结果(图8)，虽然近场结果的最大误差有所减小，但平均相对误差大于远场结果。如前所述，近场情况下，流场结构较为复杂，因此CNN-DSMC计算精度相对较低。

2.3 计算效率评估

表3为远场情况下DSMC和CNN-DSMC计算时间对比。DSMC数值模拟的计算总时间取训练集中6个算例运行的平均时间。PWS使用的CPU型号为Intel Xeon E5-2670 v3 (2.3 GHz)，使用240核并行计算。CNN-DSMC的计算基于GPU，型号为Nvidia Quadro RTX-A6000。GPU的架构使得CNN-DSMC计算可以同时处理多个算例，表3中Batch size代表算例数目。结果显示，随着算例数目的增加，CNN-DSMC计算总时间增加不多，但是平均单个算例时间从2.216 8 s降低到了0.087 3 s，相比传统DSMC的加速比在1.62×105～4.11×106之间变化，极大地提高了真空羽流的计算效率。表4给出了近场情况下的DSMC和CNN-DSMC计算时间对比。由于近场的DSMC数值模拟实际的计算域比远场小，所以DSMC数值模拟时间有所下降；且近场训练的区域要比远场训练的区域(6 m)要大，所以CNN-DSMC的计算时间稍长一些。具体表现为，CNN-DSMC相比于DSMC数值模拟的加速比在6.06×104～9.03×105之间变化，同样达到了很好的加速效果。近场情况下只统计到Batch size=20，这是由于所用GPU的显存存在限制(48 GB)。

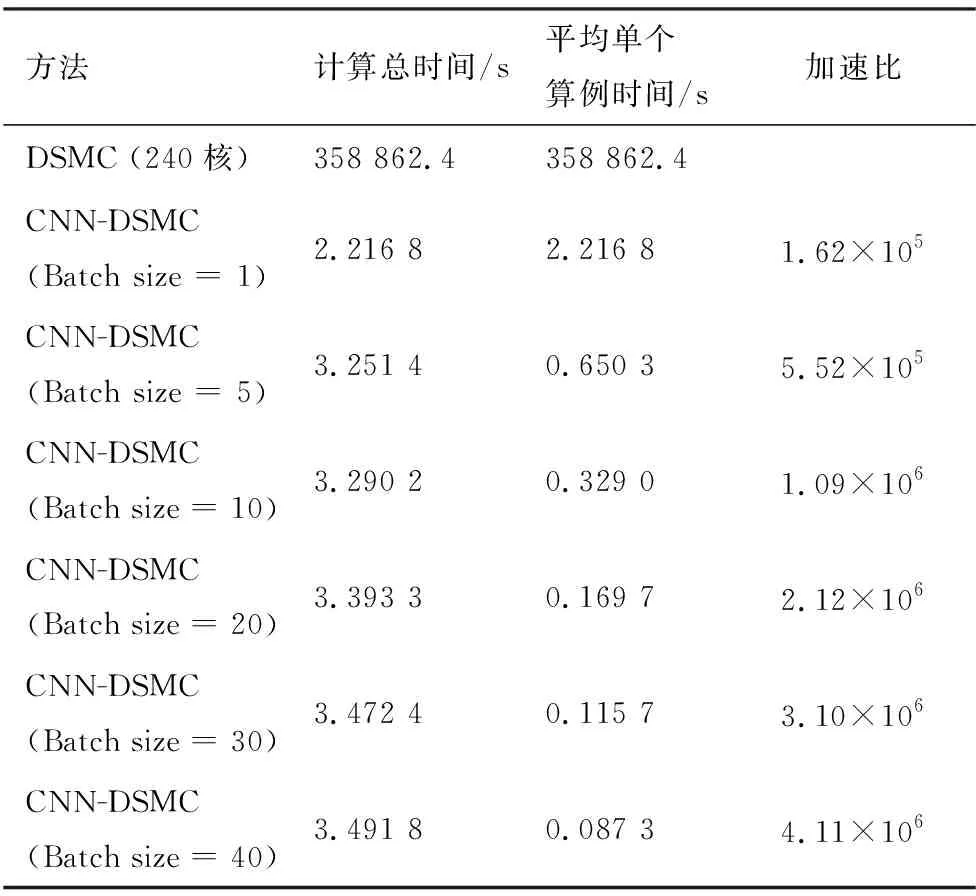
表3 远场(h>10 m)情况下DSMC和CNN-DSMC计算时间对比Table 3 Comparison of computation time between DSMC and CNN-DSMC in far-field (h > 10 m) case

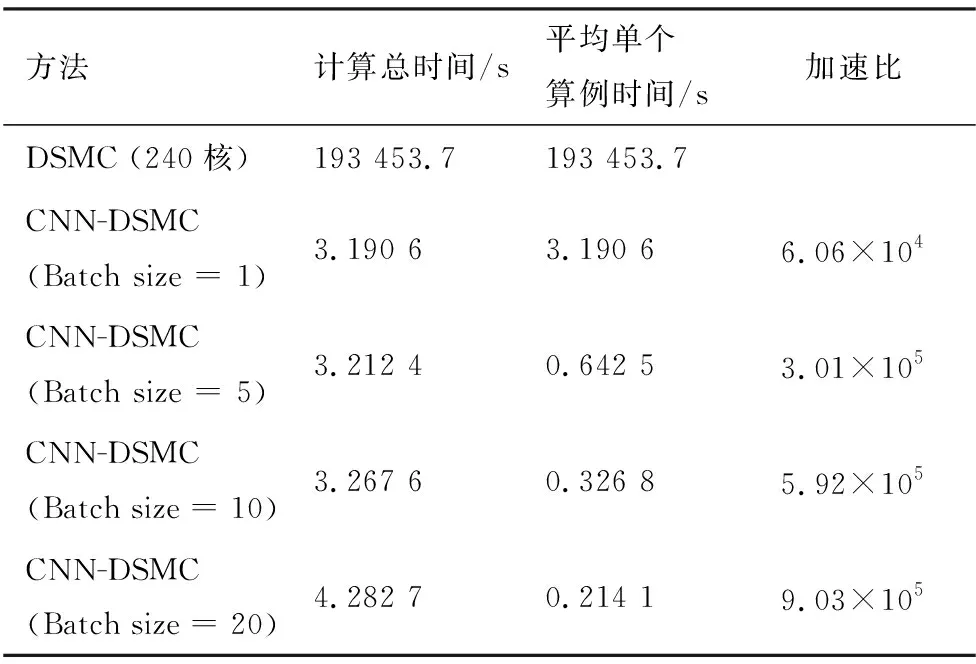
表4 近场(h≤10 m)情况下DSMC和CNN-DSMC计算时间对比Table 4 Comparison of computation time between DSMC and CNN-DSMC in near-field (h≤10 m) case

从以上分析中可以看出，CNN-DSMC方法不依赖于固定的航天器，也不仅仅局限于在化学推进羽流计算中使用。对于任意航天器的化学推进(或电推进)羽流问题，在CNN-DSMC方法训练完成后，只要输入航天器的几何外形和计算边界条件，即可完成化学推进(或电推进)流场的快速计算。

3 结 论

本文提出了一种真空羽流智能化计算方法CNN-DSMC。该方法首先将真空羽流数值模拟模型中的几何拓扑信息和边界条件信息分别抽象为符号距离函数SDF和标识符矩阵IM；然后将SDF、IM和DSMC数值模拟的流场数据作为训练集输入CNN-DSMC中的卷积神经网络，训练得到真空羽流智能化计算模型，该模型可以用于化学推进和电推进的真空羽流高精度、高效率计算。

1) 结果显示，CNN-DSMC方法计算出的真空羽流速度场和密度场无论是在远场情况还是在近场情况下都与传统的DSMC数值模拟结果基本一致。其中，在远场情况下，CNN-DSMC计算的速度和密度与DSMC数值模拟结果的平均相对误差分别为4.1%和8.2%，在近场情况下分别为6.0%和8.8%。

2) 在保证较高计算精度的同时，CNN-DSMC方法相比DSMC方法具有显著的加速效果。在远场情况下，加速比范围为1.62×105～4.11×106；在近场情况下，加速比范围为6.06×104～9.03×105。卓越的加速性能和较高的流场计算精度表明，CNN-DSMC是一个非常有应用潜力的真空羽流智能化计算方法。