相干声场的快速预测方法研究*
2022-11-04吕岩刘志红吴群仪垂杰
吕岩,刘志红,吴群,仪垂杰
(1.青岛理工大学机械与汽车工程学院 青岛,266520)
(2.工业流体节能与污染控制教育部重点实验室 青岛,266520)
引言
噪声控制中,室内声场的预测对于室内声学响应及噪声治理有重要意义。有效的声场预估能获得准确的声场特征和主要噪声源,为室内声源的布置和制定合理的噪声治理方案提供理论依据。
20世纪80年代,有学者提出众多虚声源模型来模拟室内声场,这些预测模型忽略声波之间的干涉效应,导致计算精度低、误差大。为改善这一缺陷,Wang等[1]将分析不同声波之间声压相干效应的虚源法应用于工厂车间和开放式办公室的声场预估,结果表明考虑声波相干的模型能提高声场预测精度,但因模型对声源和边界条件的简化,误差仍然突出。Lemire[2]建立了复杂虚源声场预测模型,将声波在边界上的反射视为球面波。Nobile等[3]针对单次球面波反射,提出了数值求解方法。文献[4-8]对不同声学边界条件的空间声场进行预估,拓宽了复虚源模型的预测范围,证明了将不同边界简化为不同的边界阻抗并结合虚源法能有效预估声场分布,减小预测误差,但对大尺度空间、复杂声源的预测,其计算精度有限且计算复杂度仍较高。
针对模型的预测精度,Wang等[9]对超大空间的声场进行了研究,结果表明随着空间体积的增大,声场变化的主要原因是反射声能量的改变,并基于虚源法与声压级衰减公式提出了超大空间声场的预测公式,但超大空间边界引起的散射更为复杂,使用不考虑声波干涉的模型精度仍有限。徐禄文等[10]采用声线法对影响变压器主变室外声场的因素进行了分析,其结果说明声场边界阻抗的分布对声场的分布有重要的影响,准确的边界条件是声场精度的重要前提,但其提出的预测模型仍不考虑声场的干涉。
为了提高预测精度,除了对预测模型进行改进,部分学者对声源的处理也做了相应的研究。文献[11-17]应用不同优化的噪声源模型来重构分析设备的辐射声场,预测结果的精度有了很大提升。等效噪声源模型的优化研究从另一方面提高了声场预估的精度,但同时复杂噪声源模型在应用时的计算量也随之增加。针对模型的计算效率,张朝金等[18]在射线模型和高斯射线束理论基础上,利用并行化处理对Bellhop射线模型进行了优化并开发了BellhopMP模型,该模型通过多核计算机并行计算大大提高了水下声场预估效率。此外,在声学计算领域为提高计算效率,众多学者将快速多极算法引入 计 算 之 中。Jiang等[19]将快速 多 极 算 法 引入2维声学问题,并将计算复杂度由O(N2)降低到O(NlogN)。张炳荣等[20]将快速多极算法引入基本解法,实现了一种2维声场快速预测方法。张士伟[21]将3维多极算法引入机械噪声的预测,以发动机为例,说明该方法求解噪声源辐射噪声的有效性,但仍未见快速多极算法具体应用于相干声场的预测当中。
针对封闭空间相干声场预估保证精度同时满足计算效率的要求,首先,基于ISM原理构建了虚拟接收点模型和考虑声场相干性的基本预测模型,考虑声场的多项因素以满足精度要求;其次,引入快速多极展开算法,将多点对多点的复杂映射关系转化为点集对点集的快速计算过程,对模型进行降阶计算以提高计算效率;最后,通过实验仿真验证本研究方法在复杂声场预测的高效性及适用性。
1 预测模型基本原理
1.1 复虚源相干模型
虚源法将噪声源对室内接收点的作用转化为若干阶虚源对接收点作用总和,虚拟声源与实际声源关于边界有一定的几何对称关系。虚源法原理如图1所示,其中:S为声源点;R为接收点;S(I)为虚拟源点。

图1 虚源法原理图Fig.1 Schematic diagram of the virtual source method
一个源点对接收点的作用相当于源点与无数虚源对接收点的作用之和,即

其中:P(x)为接收点声压;P0为直达声贡献;Pi为各虚源点贡献。
直达声的贡献可直接由式P0=qG(rs,rr)计算,其中:q为源强;G(rs,rr)为格林函数。而虚源的作用考虑边界的反射引入反射系数,即虚源的作用可表示为,Qj为边界的单次反射系数,得到总的反射系数代入即可求得虚源对接收点的贡献,依次求解所有虚源的贡献代入式(1)可得接收点的声压。
笔者对于单次反射系数采用式(2)的复反射系数,即

其中:k为波数;βj为第j个墙壁的法向比声导纳;dN为该路径到达接收点的传播距离;θn为第j个界面上入射方向与界面法向的夹角;i为虚数单位。
I(k,dN,βj,θn)为关于k,dN,βj,θn的函数
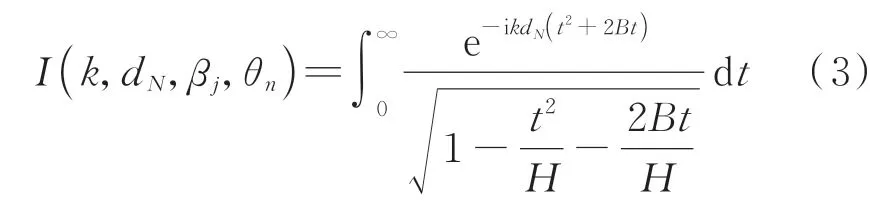
根据不同边界条件及传递路径,由式(2)和式(3)计算出单次反射系数,进而求得单个虚源点与接收点的总反射系数,代入式(1)与直达声贡献相加即可求得接收点处的声压值为

式(4)为针对不同边界条件的波叠加法基本原理,由此可知,噪声设备在空间产生的声场可由一系列配置的等效源叠加而成。等效源点的源强可由若干场点匹配而来,进而可用等效源点代替设备参与声场计算。
根据式(1)计算各个等效源点对接收点的贡献,求和即为所求声场分布。但各源点与各自虚源点的可见性判断、传递路径分析及复反射系数的求解等已占有很大计算量,而等效源点的数目一般与等效精度有关,无法选取太少,因此对各等效源点采取虚源法的计算量是巨大的。鉴于此,引入快速多极基本算法,将各等效源点的作用简化为一个参考点的贡献,从而降低计算量。
1.2 快速多极展开算法
快速多极算法的基本思想是通过将核函数即本研究的格林函数多极展开、局部展开及相应的展开转移,将源点集与接受点集中点与点的相互作用转化为两个点集单元的相互作用,原理如图2所示。其中:yi代表噪声点;xi代表接收点;X1,Y1为子晶格中心;X0,Y0为两八叉树结构的中心;M2M,L2L为子晶格中心间的作用关系;M2L为源点集与接收点集间的作用关系。现求解三维格林函数多极展开系数及展开系数转移式,以下列出关键结论及推导式。
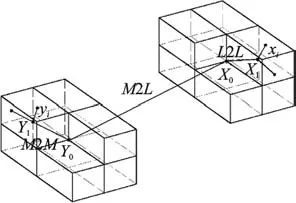
图2 3维快速多极算法示意图Fig.2 Schematic diagram of three-dimensional fast multipole algorithm
根据Graf加法原理,0阶第1类汉克函数可展开为

其中:jn(·)为n阶贝塞尔函数;()为n阶1类汉克函数;Pn()为n次勒让德多项式。
三维格林函数可表述为

其中:r″为xy间的距离;r′为Y1y间的距离;r为Y1x间的距离;γ为Y1x与Y1y的夹角。


根据上述,式(4)可表示为

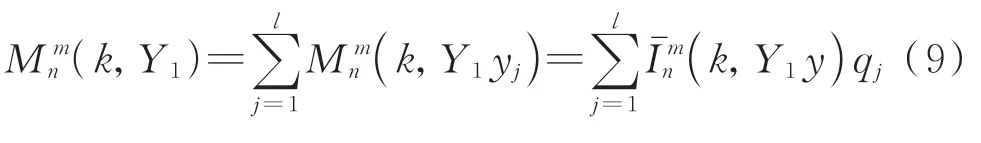
另将格林函数在Y0处展开,得到展开系数转移式

式(12)中,Wn,n′,m,m′,l为

通过多极展开系数式(9)及展开转移系数式(10)即可将各子晶格作用转移至父晶格,逐级由最底层转移至最高层,从而实现将源点子集中各点对接收点的作用转化为子集整体对接收点的作用。
2 相干声场快速预测方法
本研究预测模型主要基于虚源法,将室内任意噪声源转化为等效源点集,引入快速多极算法计算虚源产生的声场,而直达声采用传统基本解法。具体实现步骤如下。
1)对噪声源设备进行等效处理。根据等效源思想,将设备产生的声场等效为若干单极子点源的叠加声场,若已知声源边界条件则用式(4)求解各源点源强;若未知则采用声强或声全息的方法重构声源[16-17]。声源的源强矩阵及位置矩阵分别为

其中:qi为第i个等效源源强;qi(x,y,z)为第i个等效源位置坐标。
2)对等效源点子集建立3维八叉树结构。笔者主要针对源点子集进行简化计算,只选取1个包含所有源强点的立方体,等分这个立方体得到第2层,依次对含有源点的小立方体进行划分直至最末层立方体中的源点数量小于设定的阈值。根据八叉树结构建立各级分层中心点的源强及位置坐标矩阵为
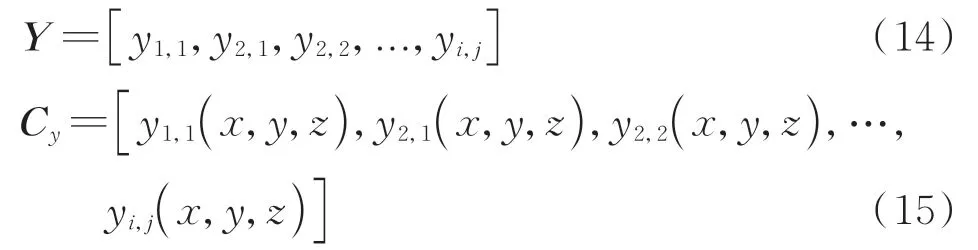
其中:yi,j为第i层第j个晶格中心的源强;yi,j(x,y,z)为中心的坐标。
根据等效源点所在晶格,将等效源点进行范围划分,一般晶格内源点数量阈值为1,即1个晶格内含1个等效源点。
3)建立虚源模型。若对等效源点子集建立虚源模型,则需建立相应阶数的源点八叉树结构,模型计算量较大,因此建立虚拟接收点模型,建立接收点关于边界的虚拟接收点子集,而噪声源对接收的作用表示为噪声源对每个接收点贡献的集合。在图1中与虚拟源相似,可得虚拟接收点(xs,ys,zs)在空间的分布为

其中:(L,W,H)为边界的尺寸。
为计算方便将坐标原点置于室内某一顶点,另l∈(-∞,∞),n∈(-∞,∞),m∈(-∞,∞),因此给定了1组(l,n,m)的值就决定了1个特定的虚拟接收点。由此建立虚拟接收点的声场响应值矩阵及位置矩阵为

其中:si为第i个虚拟接收点的响应值;si(x,y,z)为虚拟接收点位置。
由边界的尺寸可得,边界SL0,SL1,SW0,SW1,SH0,SH1在3维空间的虚拟边界分布分别为SL0+2lL,SL1+2lL,SW0+2nW,SW1+2nW,SH0+2mH及SH1+mH,l,n,m∈(-∞,∞)。S分别表示各边界面,当l,n,m=0时为6个实际边界面。
4)上行历遍。在源强八叉树结构中,根据等效源点位置矩阵式(13)与八叉树结构晶格中心位置矩阵式(15),利用式(9)与式(10)计算结构各层晶格的多极展开系数及转移系数,将各等效源点作用逐级向父层转移,直至最高层,将整个点集的作用转化为中心Y0的作用QY0。
5)室内声场计算。根据虚拟接收源位置矩阵与源强八叉树结构中心Y0的坐标关系建立传递路径函数,不同的虚拟边界对应不同的边界阻抗,求解路径与空间虚拟边界的交点从而确定该路径的传递距离、反射次数、各单次碰撞反射系数与总的反射系数,建立各接收点对应的反射系数矩阵

逐次求解Y0对所有虚拟接收的贡献

所有虚拟接收点均满足多极算法的前提,根据步骤2和4建立的作用点Y0与步骤3建立的虚源模型计算所有反射声的贡献,根 据 步 骤1的等效源点模型用传统基本解法计算直达声P0,避免对多极算法的条件判断。将直达声与反射声相加即得到室内任一场点的声场信息。
3 实验与仿真分析
3.1 仿真分析
3.1.1 仿真示例1
为对比FMA-ISM方法的计算精度,针对某长方体空间进行数值仿真模拟,仿真模型示意图如图3所示。为了便于对比其他方法,模拟长方形空间参数为1 000 mm×500 mm×500 mm,设置8个声源和9个接收点,每个单极子声源振幅A设为0.1,声源及接收点的位置参数如表1和表2所示。墙面边界阻抗属性按照数据库中普通厂房钢架结构材料定义。
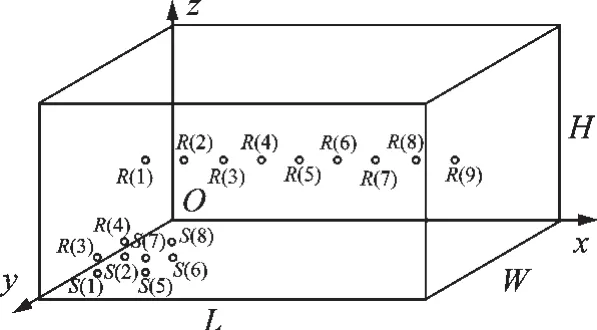
图3 仿真模型示意图Fig.3 Schematic diagram of the simulation model
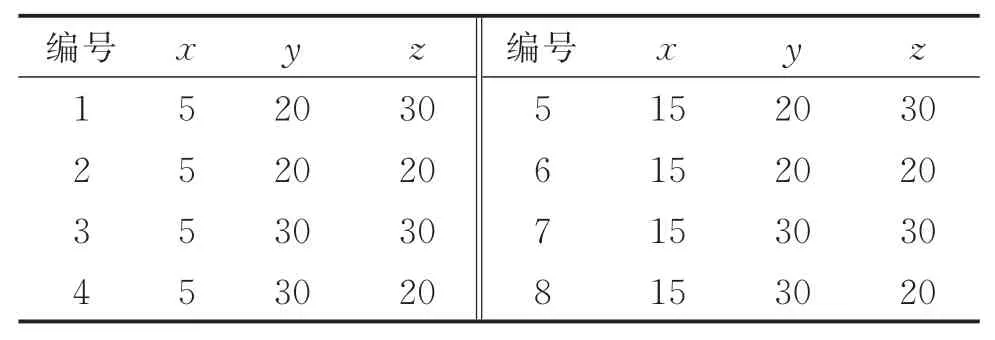
表1 声源位置参数表Tab.1 Location parameters of sound source mm

表2 接收点位置参数表Tab.2 Location parameters of receiver point mm
为验证本研究方法的计算效率和精确度,现分别利用FMA-ISM方法、有限元方法及传统声线法对上述模型进行计算。由于基于波动理论的有限元方法精度较高,在此以有限元方法进行对比。FMA-ISM方法在Matlab下计算,计算取前5阶虚源。声线法利用Soundplan计算,Soundplan利用传统的声线法与虚源法,计算时不考虑声波相干性。计算在同一设备进行,计算机CPUi5-8600,双核6线程,运行内存为8 G。
本仿真算例中有限元网格划分大小为10 mm,计算频率范围为100~5 000 Hz,计算步长为10 Hz,接收点R7计算结果对比如图4所示。由图可见,由于有限元方法与FMA-ISM方法均考虑相位影响,2种方法计算结果有相同的声压级变化趋势,反映了声波间的相位干涉。而有限元考虑了空间自身模态,其变化与FMA-ISM模型略有不同。另外,由于声线法不考虑相位,只考虑能量的叠加,使得变化趋势很小、误差较大。
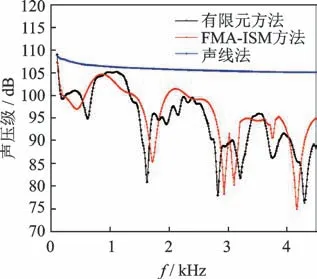
图4 接收点R7计算结果对比图Fig.4 Comparison of calculation results of receiving point R7
进一步对比3种方法,采用绝对误差值对比FMA-ISM方法、传统声线法与有限元方法的误差

其中:PFin为有限元计算结果;PMod为FMA-ISM方法计算结果;PSou为声线法计算结果。
接收点R7误差结果对比如图5所示。由图可见:FMA-ISM方法的绝对误差基本在6 dB以下,个别与房间模态对应频率达到7~9 dB,平均误差为3 dB;声线法的绝对误差均在8 dB以上,部分达到了20 dB以上,平均误差达到了12 dB。

图5 接收点R7误差结果对比图Fig.5 Comparison of the error of the receiving point R7 result
表3为3种方法计算时间对比。由表可知,FMA-ISM方法在保持一定误差精度的前提下,计算效率较有限元方法提高50%以上。但是本算例模型较为简单,随着模型复杂度的进一步提高,有限元方法的计算时间会大大增加。另外,声线法计算时间虽然也较低,但结果误差较大,不满足计算精度要求。

表3 不同方法计算时间对比Tab.3 Comparison table of calculation time by different methods s
考虑在同一频率(500和4 000 Hz)下的各接收点结果,如图6和图7所示。由图可见,本研究方法计算结果均与有限元结果变化趋势趋于一致,而声线法计算结果变化趋势不明显且部分接收点差值较大。结果对比反映出声波的相干效应对声场的影响较大,尤其当声源环境与空间环境均较复杂时,忽略相位影响将导致结果有误。
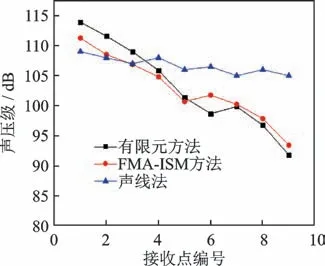
图6 接收点R1~R9在500 Hz计算结果对比图Fig.6 Comparison of calculation results of receiving points R1~R9 at 500 Hz

图7 接收点R1~R9在4 000 Hz计算结果对比图Fig.7 Comparison of calculation results of receiving points R1~R9 at 4 000 Hz
考虑各方法的误差因素。有限元方法的计算效率直接与空间大小和网格大小有关,同时仿真计算需要对边界条件进行合理的简化,且有限元声源输入条件难以准确获取造成误差。Soundplan作为一种大型声场仿真软件,固化的程序使得操作较为简单,计算厂区大范围的声场计算效率高,但其精度受算法限制,达不到误差要求。FMA-ISM方法建立在现有虚声源的基础上,计算代码简单,易实现,误差因素同有限元相同,在准确的声源与边界条件下,能获得较好的计算结果。
3.1.2 仿真示例2
为进一步对比FMA-ISM方法与传统ISM方法的误差及计算效率,另针对某矩形空间声场进行仿真计算。仿真模型如图8所示。房间尺寸参数为10 m×5 m×5 m,声源随机分布在x∈(2 m,3 m),y∈(2 m,3 m),z∈(2 m,3 m)的立方体内,声源由单极子源构成,单个源强100 dB,数目分别为8,16,32,64,128及256,接收点位于(7.5 m,2.5 m,2.5 m)。为对比空间参数对模型计算精度影响,现分别取3类空间边界:①空间各边界均为理想刚性边界;②空间各边界吸声系数均为0.1;③空间顶部吸声系数为0.3,其余边界均为0.1,各边界的吸声系数处处相等。计算在同一设备进行,计算2 000 Hz声场分布,计算过程取5阶虚源,计算结果与误差对比如图9和图10所示。其中:黑色线为ISM方法计算结果;红色线为FMA-ISM方法计算结果。

图8 仿真模型示意图Fig.8 Schematic diagram of the simulation model

图9 仿真计算结果对比Fig.9 Comparison of simulation results

图10 仿真计算结果误差对比Fig.10 Error comparison of simulation results
根据计算结果,在刚性边界下FMA-ISM方法与传统ISM方法结果趋于一致,绝对误差在2 dB内。随着边界条件的复杂,两者计算误差增大,第3类边界条件计算结果最大误差达6 dB。分析原因为FMA-ISM方法简化源点的作用为源点集合的作用,针对声源的可见性判断、总吸声系数的求解等仅在源点集中心计算,而传统ISM方法针对每一源点逐个分析计算,由此产生误差,且当边界条件差别越大,误差越大,但二者平均误差基本满足工程计算要求。
各类边界的计算时间如表4所示。由表可知,传统ISM方法因对源点逐个分析,导致计算时间随着源点数目的增加急剧增加;FMA-ISM方法随源点数目的增加,计算时间增量较少,增加时间主要为源点集八叉树结构复杂度的增加,而传播分析时间增加较少。因此,改进的FMA-ISM方法可有效提高ISM方法的计算效率。

表4 不同模型计算时间对比表Tab.4 Comparison table of calculation time of different models s
3.2 实验分析
为验证FMA-ISM方法对声场预估的适用性,在消声室针对某噪声设备进行声场预估分析。消声室边界条件简单,易实现计算要求,实验测试现场如图11所示,所用消声室为金属尖劈半消声室,消声室尺寸为10 m×8 m×3.7 m。噪声源设备为某工业除湿机,除湿机尺寸为0.4 m×0.5 m×1.5 m。采用声强法对除湿机本体噪声进行测试,除湿机声功率为94.77 dB。

图11 实验测试现场图Fig.11 Experimental test scene
将除湿机置于消声室顶角处,测量除湿机水平5 m×5 m范围内声场分布及东侧2 m处2 m×2 m垂直立面的声场分布。水平测点高度为1.2 m,测点间距为0.3~0.4 m,共200个测点,测点布置如图12所示。垂直立面测点间距为0.2 m,共100个测点。测试用仪器为Norsonic150声振分析仪,声强探头为GRAS 50AI-C。水平面和垂直立面的声场分布分别如图13和图14所示。

图12 现场测点布置图Fig.12 Layout of on-site measuring points

图13 水平面声场分布图Fig.13 Horizontal sound field distribution diagram

图14 垂直立面声场分布图Fig.14 Distribution diagram of vertical elevation sound field
根据测试结果,在消声室内四周及顶部边界的吸声系数较高,反射声主要由底部反射贡献,声场分布与自由场接近。运用等效源基本思想,将除湿机等效为规则布置的单极子点源组合,等效源点数量分别为8和64。分别利用FMA-ISM及ISM方法对立面的声场进行预估计算,选取场点中35个测点作为评价点,实测值与预估结果如图15所示。图中A类折线为现场实测值;B,D类折线为FMA-ISM方法,等效源点数分别为64和8的预估计算值;C,E类折线为ISM方法,等效源点数分别为64和8的预估计算值。根据对比结果,随着等效源点数的增加,预测值与实测值趋于一致,ISM方法的计算结果精度高于FMA-ISM方法。为进一步分析误差,采用绝对误差对比分析各模型预估精度

图15 选点计算结果对比图Fig.15 Comparison of calculation results of point selection

其中:Pcal为理论计算值;Pre为实际测量值。
图16为误差率对比图。图中A,C类折线为FMA-ISM方法,源点数为64和8的预测误差;B,D类折线为ISM方法,源点数为64和8的预测误差。当源点数增加到64时,FMA-ISM方法与ISM方法的误差均保持在2 dB内。随着等效源点数量的增加,模型误差减小,源点数增加到一定量后模型误差趋于一定值,但随着源点数的增加,模型计算量也随之增加。表5为2类模型的计算时间,可以看出,随着源点数的增加,ISM方法的计算时间急剧增加,而FMA-ISM方法的增加量较小,这与仿真示例结果一致。本研究实验所用除湿机尺寸较小,源点数增加至64已可满足要求。针对不同噪声源设备,根据设备尺寸及噪声产生机理合理选取等效源点数目,既可保证模型计算的精度也使得计算量控制在一定范围内。通过实验证明FMA-ISM模型可应用于现实的声场预估。
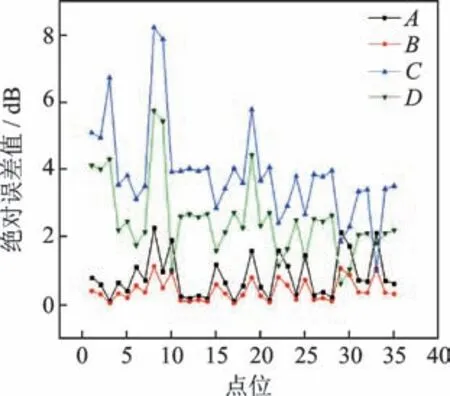
图16 选点计算结果误差对比图Fig.16 Comparison of errors in calculation results of point selection

表5 不同模型计算时间对比表Tab.5 Comparison table of calculation time of different models s
4 结论
1)通过复虚源方法与快速多极算法构建了封闭空间的声场预估模型(FMA-ISM),以解决封闭空间声场预估精确度不高、计算效率低等问题。通过复虚源原理与等效源方法建立虚拟接收点模型,对声源及边界条件进行等效后预估声场,预估结果与实验实测值误差保持在3 dB内,能满足预估精度的要求。引入快速多极算法对模型进行简化计算,与其他方法对比,针对一定复杂度的空间声场计算效率可提高50%以上,在保持预估精度的前提下大大提高了计算效率。
2)采用实验与仿真对模型进行验证,并与其他预估模型及方法进行对比。仿真1验证了FMA-ISM方法结果与精度较高的有限元法结果趋于一致,两者平均误差在3 dB内,精度可满足工程应用要求。仿真2验证了在相同计算条件下,FMA-ISM通过对虚源贡献的降阶分析,计算效率较传统ISM方法提高50%以上。最后,通过实验室示例验证了FMA-ISM方法在室内声场预测的高效性及适用性。
