耦合Helmholtz共振消声器的设计及参数分析*

韩雷，季宏丽，裘进浩

（南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

引言

传统的Helmholtz共振消声器通常由共振腔通过颈部与主管道连通构成，广泛用于低频噪声的抑制［1-6］。然而，由于Helmholtz共振器的谐振特性，消声器只有1个消声峰。因此，通常使用多个具有不同谐振频率的共振器相结合实现在较宽的频带范围内的噪声衰减［7-9］。Xu等［10］设计了一对串联组合的颈腔结构（颈-腔-颈-腔），能够在低频范围内产生2个谐振峰，并可以通过改变结构参数来控制消声峰频率，使双Helmholtz共振器串联结构成为理想的消声元件。此外，对内插颈［11］、圆形同心腔［12］、圆形非同心腔［13］以及内衬吸声材料［14］等物理参数对共振特性的影响也进行了相关研究。Griffin等［15］设计了一种由2个Helmholtz共振器和1个耦合元件组成的机械耦合Helmholtz共振器，可以在更大的带宽上实现噪声的衰减。

除上述无源方法外，还采用了无源-有源混合方法来拓展噪声衰减带宽。文献［16-17］开发了一种基于半主动控制定律改变共振腔内活塞位置以改变腔体体积，从而调整消声特性。Mcdonald等［18］提出了一种调控方式类似于Matsuhisa的自适应Helmholtz共振器，根据共振腔与主管道系统之间声压的相位关系同时调节共振腔体积和颈部长度。高林等［19］基于半主动控制算法对Helmholtz共振器的颈部横截面积进行调控，实现多个传递损失消声峰。

利用多个共振器相结合改善消声频带的方法大大增加了结构的体积。虽然无源-有源混合的方法可以有效地抑制低频噪声，但是控制系统中包含传感器、执行器、实时控制器、信号调节和功率放大器等部件，使噪声衰减系统的成本大幅提高［20］。因此，为了在不改变原有尺寸的情况下改善消声性能，笔者提出了一种在共振腔内安装有柔性板结构的机械耦合Helmholtz共振消声器。柔性板结构由轻薄的柔性面板及附加质量块组成，将共振腔分为上下2部分。入射声波激励起柔性板结构产生振动，使其成为上下2部分腔体之间的耦合元件。柔性板结构与上部腔体（背腔）相结合作为原系统的附加自由度，从而将原Helmholtz共振峰一分为二，有效地改善了传统Helmholtz共振消声器的声学性能。

1 耦合Helmholtz共振式消声器

基于传统共振消声器所提出的耦合Helmholtz共振式消声器模型如图1所示。将附加有质量块的柔性板结构放置在Helmholtz共振腔中，使共振腔分隔为上下2部分腔体（腔体1和腔体2）。腔体之间通过柔性板结构相互耦合，可以认为腔体2和柔性板结构组合为新的附加自由度系统，从而使传统Helmholtz共振器进化为2自由度共振系统。

图1 耦合Helmholtz共振消声器示意图Fig.1 The diagram of the coupled Helmholtz resonance muffler

共振腔内的柔性板附加有非对称形状的质量块，质量块可以是任何其他形状，如环形或圆柱形。由于作为耦合元件的柔性板对上下腔体的共振具有直接影响，因此附加质量块的目的在于调整柔性板的振动特性，以期改变共振消声器的消声特性。图2所示为柔性板结构的示意图，4个质量块完全相同且为半圆形，两两对称分布在柔性板两侧。对称分布的2个质量块的圆心与柔性板中心在同一直线上，且质量块之间圆心到圆心的距离为2(r+lm)。柔性板结构可以被入射声波激励产生振动，且其四周边界通过上下腔体的刚性壁夹紧为固支边界条件。柔性板与质量块之间的连接为刚性连接，消声器的固体结构部分均假定为声学刚性壁面。

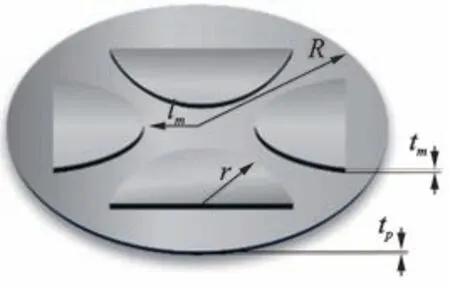
图2 柔性板结构示意图Fig.2 The diagram of the flexible plate with mass blocks

2 理论基础

由于管道尺寸远小于低频范围声波的工作波长，因此可以假定在管道中沿轴线方向传播的入射声波为平面波。耦合Helmholtz共振消声器的2维理论模型可以简化为如图3所示，其中数字标注的位置表示对应的截面，此处主要用于标明后续计算中管道内不同截面处的声学阻抗。

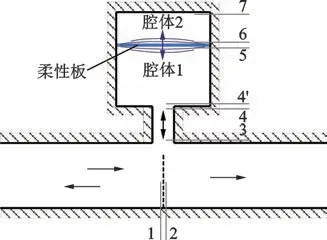
图3 消声器2维理论模型Fig.3 2D theoretical model of the muffler

共振器的颈部和腔体1均可视为均匀截面管结构。基于上述平面波假设，颈部和腔体1对应的入口处的声学阻抗［21-22］可以分别表示为

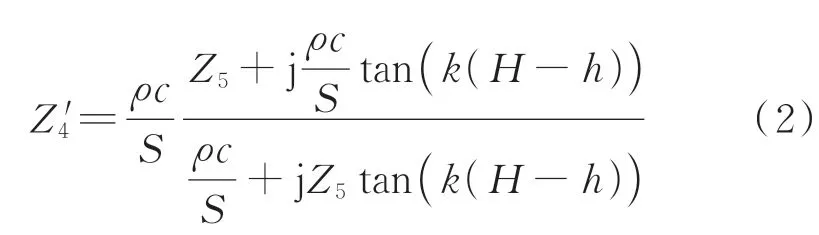
其中：ρ和c分别为空气密度和声速；k为声波波数；s和S分别为颈部和腔体的截面积；H和h分别为共振腔总深度及腔体2的深度；Z3，Z4，Z′4和Z5分别为截面3，4，4′和5处对应的声阻抗；l′=l+tw+0.85d为颈部的声学长度［21］；tw为颈部壁厚；d为 颈 部内径。

由于腔体2的顶部被刚性壁封闭，因此根据式（2）可得截面6处的声学阻抗为

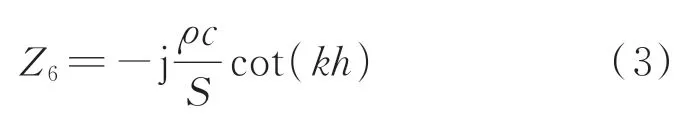
其中：当腔体2的深度远小于声波波长时，式（3）可进一步近似为Z6=-jρc(Skh)。

根据Beranek声学变压器理论［23］，当声波在截面积不连续的管道中传播时，对于在截面突变交界面两侧的声阻抗存在一个转换比。因此，颈部与腔体1连接处即截面4和4′处的声阻抗存在如下关系

根据式（1）～（4）的推导，只要得到截面5和6之间的声阻抗关系即可得到截面3处的声阻抗Z3。假设图3中柔性板没有附加质量块，则其运动方程根据文献［24］中的推导公式可以表示为

老马说：“这就是你的事了，但我认为死者真正死因是急性肾衰竭。而不是以往的多数死于失血过多，尸体有很明显的尿中毒症状，当然具体的死因还需要进一步验证。”老马边说边用扩张器撑开死者伤口，又说：“你看，伤口中还进行了必要的止血手术，而且肯定还进行过严格的消毒程序，不然在这么热的天伤口部分肯定先腐烂，但是你看，伤口部位腐败程度反而低于身体其它部位。”

其中：xp为板的位移；r为板上任意位置；ρs和tp分别为板的密度和厚度；D为无内阻尼弯曲刚度；p5和p6分别为截面5和截面6处的声压幅值。

假设只考虑低频范围内起主导作用的结构第1阶振型，根据文献［24］中对于柔性板振动特性的理论计算，可得截面5处的声阻抗为

根据主管道截面1，2和3处的声压和质量速度连续性条件，将声压和质量速度作为两个状态变量，利用传递矩阵法可以得到如下矩阵关系［25］

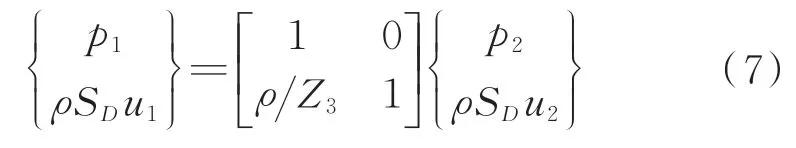
因此，耦合Helmholtz共振消声器的传递损失TL可以确定为

结合式（1）～（4）以及式（6）即可获得颈部截面3处的声阻抗Z3，进而得到消声器的传递损失TL。通过以上对安装有简单柔性板的消声器的TL推导过程可知，柔性板的声-振特性及安装位置对TL具有显著的影响。基于此结论，设计了如图2所示的柔性板结构，以提高其振动特性的可调性。然而，对于附加了质量块的柔性板结构，其运动方程将随之更加复杂化，不便于进行解析计算。因此，在后续的研究中，将借助于数值仿真和实验验证定性地分析柔性板结构的相关几何参数及安装位置对TL的影响规律。

3 参数影响规律分析

表1 柔性板和质量块的材料物理属性Tab.1 The material physical properties of flexible plate and mass blocks

表2对应的耦合Helmholtz共振消声器以及传统Helmholtz共振消声器的传递损失曲线如图4所示。显然，柔性板结构的引入将原TL消声峰一分为二，有效地改善了其声学性能。为了定性分析柔性板结构参数对消声特性的影响，设计以下不同的物理参数值，如表3所示，其中A～E表示各结构参数所选取的5种不同参数值。系统地改变其中一个参数值而保持其他结构参数为初始值不变，分析各结构参数对传递损失的影响规律。

3.1 结构参数的影响

首先，对质量块不同厚度tm情况下对应的TL进行分析，过程中其他结构参数保持表2所示初始值不变。图5为不同tm对应的传递损失曲线和消声峰频率fpi变化的曲线。由图可见，随着tm的增大，第1和第2消声峰对应的频率均向低频方向偏移。显然，随着质量块厚度的增加，柔性板结构的共振频率也将变低。由于消声器声学特性与柔性板结构的振动特性密切相关，因而质量块厚度的增加导致耦合Helmholtz共振消声器的消声峰频率向低频方向偏移。

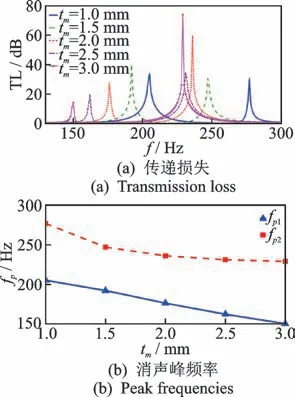
图5 质量块不同厚度对应的传递损失和消声峰频率Fig.5 Different thicknesses of mass block correspond to transmission loss and peak frequencies

为了进一步探究消声峰对应的物理消噪机理，图6展示了在消声峰对应频率下柔性板结构的法向线位移以及腔体1和腔体2的内部声压云图随着质量块厚度的变化情况。由图可知，第1消声峰对应频率下柔性板的线位移随着tm的增大而增大，表明柔性板的振动增强，声波透过柔性板由腔体1进入腔体2的能力也随之提高，同时，如图6（c）第1行声压云图所示，腔体2内部的声压随着tm的增加而升高，且第1消声峰对应的频率逐渐接近柔性板与腔体2之间的耦合谐振频率154 Hz；相反，随着tm的增大，第2消声峰对应频率下柔性板的线位移变小，即其声学刚性增强，同时，腔体1内部的平均声压也随之升高，第2消声峰对应的频率逐渐接近于腔体1所引入的共振频率224 Hz。因此，消声器的消声峰主要由腔体1和腔体2与柔性板结构之间产生耦合共振而依次引入，且消声峰频率变化的上下限则主要取决于腔体2和柔性板结构组成的耦合系统对应的谐振频率，以及腔体1对应的谐振频率。

图6 在消声峰频率下质量块不同厚度对应的柔性板结构线位移以及腔内平均声压Fig.6 Different thicknesses of mass block correspond to line displacements of the flexible plate and the average pressure in the cavity at resonance frequencies

其次，根据式（5），质量块的布放位置对柔性板的振动特性同样具有一定的影响。图7为质量块到柔性板中心不同距离lm对应的传递损失、消声峰频率和柔性板结构振动模态。当lm变大时，TL的第1和第2消声峰频率均向高频方向偏移。分析柔性板结构的振动模态，如图7（c）所示，质量块间距离的增加对柔性板中心位置的影响越来越小，同时增加了柔性板四周的等效刚度，因而柔性板结构的共振频率随着质量块距离的增加向高频方向偏移，进而影响了消声器TL峰值频率的变化。

图7 质量块间不同距离对应的传递损失、消声峰频率和柔性板结构振动模态Fig.7 Different distances between mass blocks correspond to transmission loss and peak frequencies as well as vibration modal of flexible plate

此外，柔性板厚度变化对消声器传递损失以及消声峰频率的影响如图8所示。随着tp的增加，柔性板的弯曲刚度变大，其特征频率也随之提高，因而消声峰频率向高频方向偏移，同时，入射声波激励柔性板产生的振动减弱，导致腔体2与柔性板的耦合效应降低。图8（a）中插图所示为当tp分别增加至0.8 mm和1.0 mm时传递损失的第2个消声峰，其对应的消声峰幅值较小，基本可忽略不计。此时，第1消声峰对应的频率基本保持不变，分别为222 Hz和223 Hz，与腔体1单独存在时产生的消声峰频率224 Hz相近。因此，当柔性板厚度增加至一定数值时，可近似将其等效为声学刚性壁面，此时TL的消声峰主要是由腔体1的共振引入。

图8 柔性板不同厚度对应的传递损失和消声峰频率Fig.8 Different thicknesses of flexible plate correspond to transmission loss and peak frequencies

最后，由于柔性板结构在共振腔中的位置对其内部腔体的声学阻抗具有直接影响，因此有必要探讨腔体2的深度h对消声器TL的影响。图9为不同h对应的传递损失及消声峰频率变化曲线。由图可见，随着h的增加，第1消声峰频率逐渐降低，第2消声峰频率则逐渐升高。为了探究内在原因，分析了柔性板结构的线位移及腔体声压云图，如图10所示。随着腔体2深度的增加，第1消声峰对应频率下柔性板的振动逐渐增强，消声峰主要由腔体2与柔性板间的耦合谐振引入，因而第1消声峰对应的频率随着腔体2深度的增加向低频方向偏移；相反，第2消声峰对应频率下柔性板结构的线位移随着腔体2深度的增加而减弱，第2消声峰的引入主要由腔体1的谐振产生。根据Helmholtz共振频率fr=可知，h的增加使得腔体1的谐振频率升高，即第2消声峰频率向高频方向偏移。

图9 腔体2不同深度对应的传递损失和消声峰频率Fig.9 Different depths of cavity 2 correspond to transmission loss and peak frequencies

图10 在消声峰频率下腔体2不同深度对应的柔性板结构线位移以及腔内平均声压Fig.10 Different depths of cavity 2 correspond to line displacements of the flexible plate and the average pressure in the cavity at resonance frequencies

3.2 参数影响的验证分析

在不同的结构尺寸下，进一步验证以上各个结构参数对TL的影响规律。图11为具有不同质量块厚度的柔性板结构随着质量块间距离的变化引起的TL消声峰频率变化曲线。质量块间距离的变化对消声峰频率的影响与图7保持一致。另外，随着质量块厚度的增加，消声峰频率在不同的质量块距离下均向低频方向偏移，与图5一致。同时，第1消声峰频率向低频方向偏移的幅度随着质量块距离的增加而减小，验证了质量块对柔性板中心区域振动的影响随着质量块间距离的增大而减小的结论。

图11 质量块不同厚度对应的第1和第2消声峰频率随质量块间距离的变化Fig.11 Different thicknesses of mass block correspond to the first and second peak frequencies vary with different distances of mass blocks

将具有不同厚度的柔性板分别放置在共振腔中不同位置对TL消声峰频率的影响如图12所示。与图8结论相同，消声峰频率随着柔性板厚度的增加逐渐向高频方向偏移。由于当柔性板厚度增加至一定程度时，第1消声峰主要由腔体1的共振引入。因此，当tp大于0.5 mm时，随着h的继续增加，第1消声峰频率的变化与图9不同，反而向高频方向偏移。另外，当tp=0.5 mm时，柔性板的特征频率为215.22 Hz，与无柔性板结构的Helmholtz共振频率213 Hz非常接近，因而尽管h不同，第1消声峰频率几乎相同。

图12 腔体2不同深度对应的第1和第2消声峰频率随柔性板厚度的变化Fig.12 Different depths of cavity 2 correspond to the first and second peak frequencies vary with different thicknesses of flexible plate

4 实验验证

为了验证以上对耦合共振消声器结构参数分析的正确性，借助BSWA TECH阻抗管系统采用双负载法［26］对消声器的传递损失进行实验测量。实验过程中考虑了腔体2的深度h、柔性板厚度tp以及质量块厚度tm这3种结构参数。实验装置如图13（a）所示，质量块与柔性板之间、柔性板边缘与腔体1和腔体2的刚性壁之间均采用AB胶粘接，以实现刚性连接的条件。消声器主通道与阻抗管连接处采用硅橡胶密封，激励声源为频率60～500 Hz的白噪声。图13（b）为传统Helmholtz共振消声器与耦合Helmholtz共振消声器传递损失曲线的实验测量结果对比，其中腔体2深度h为49.5 mm，其他结构参数如表2所示。

图13 消声器传递损失测量的实验装置和安装柔性板前后消声器的传递损失曲线对比Fig.13 The experiment setup used to measure the transmission loss of muffler and the transmission loss spectrums of the muffler with and without flexible plate

图14为消声峰频率随着3个结构参数h，tp和tm的变化曲线。其中，下面两幅图为保持h=49.5 mm的情况下分别改变柔性板和质量块的厚度测量的结果。对比实验测量和数值仿真的结果，二者基本吻合，进一步验证了以上对耦合共振消声器结构参数影响规律分析的正确性。

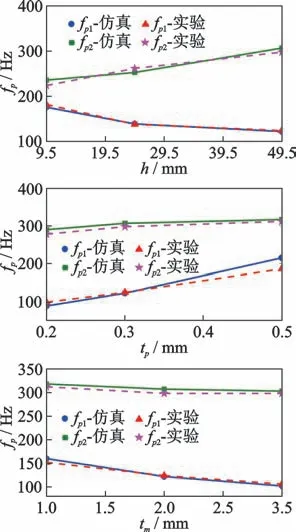
图14 消声峰频率随不同结构参数变化的仿真与实验结果对比Fig.14 Peak frequencies obtained by simulation and experiment vary with different structural parameters

5 结论

1）耦合Helmholtz共振消声器产生的消声峰主要由腔体1和腔体2与柔性板结构之间产生耦合共振引入，且消声峰频率变化的上下限主要取决于柔性板与腔体2构成的附加自由度系统对应的谐振频率，以及腔体1对应的谐振频率。

2）通过增加附加质量块的厚度可以降低柔性板的共振频率，从而使消声器的消声峰频率向低频方向偏移。

3）柔性板的厚度与其弯曲刚度成正比。增加柔性板的厚度将使其共振频率向高频方向偏移，进而提高消声峰频率。但是，当柔性板厚度增加至一定程度时，其声学特性逐渐接近刚性壁面，导致柔性板结构及背腔形成的附加的自由度失去作用。

4）柔性板结构与腔体之间产生耦合效应的振动主要集中在中心区域，因此，质量块间距离的增加使柔性板结构的共振频率逐渐升高，且质量块对其振动特性的影响逐渐减弱。

5）柔性板结构在腔体中的位置变化改变了腔体1和腔体2与柔性板结构的耦合谐振频率。根据结论（1）可知，随着腔体2深度的增加，消声峰频率间的差距将逐渐增大。