基于神经网络和子空间的非线性系统载荷识别*

庞志雅，马志赛，丁千

（1.天津大学机械工程学院天津，300350）

（2.天津市非线性动力学与控制重点实验室 天津，300350）

引言

非线性系统广泛存在于现实世界中，例如物体之间的接触和滑动会引起摩擦非线性［1］，加工超差、装配误差和使用磨损等因素会造成结构连接部位出现间隙非线性［2-3］等。随着工程应用领域的不断拓展和设计需求的日益增长，非线性系统的动力学反问题受到了越来越多的关注。结构动力学反问题包括系统辨识和载荷识别2类基本问题，但在处理和解决实际工程问题时，系统辨识和载荷识别常常是相互耦合的。

通过系统辨识手段描述非线性系统的动态特性和行为是解决其动力学问题的关键，非线性系统辨识已逐渐成为结构动力学领域的研究热点之一。文献［4-5］回顾了近几十年来结构动力学中非线性系统辨识的研究进展，并对线性化、时域、频域、时频分析、非线性模态分析、黑箱建模和模型更新等参数估计方法进行了综述，其中时域法由于无需将数据转换至频域，凭借可有效避免泄露和混频等优点得到了迅速发展。文献［6-7］提出了一种将非线性项视作标称线性系统的内反馈力，进而利用线性子空间理论对非线性系统进行辨识的时域方法，即时域非线性子空间辨识方法，该方法具有良好的调节和计算能力，可以同时辨识多个非线性项，并且克服了由于信号相关性增加导致非线性项和标称线性系统频响函数在共振区附近估计精度较低的缺点。Noël等［8］采用时域非线性子空间方法对含强非线性特征的卫星结构进行了辨识，得到其标称线性系统的模态参数和非线性项，并在辨识精度和计算效率等方面与频域非线性子空间方法进行了比较。Sun等［9］采用时域非线性子空间辨识法对全动舵面进行了辨识，指出该方法由于利用几何框架和数值线性代数分解，具有一定的鲁棒性和高性能。Zhang等［10］将非线性系统分为标称线性系统和局部非线性部分，分2步估计标称线性系统的频响函数和非线性部分的系数，提高了时域非线性子空间方法的精度与可靠性。

虽然子空间方法具有优良的性能，但对于非线性系统来说，非线性描述函数的选定仍然是辨识过程中的难点之一。例如，现有的多项式拟合法［11］、三线性函数法［12］等都会使辨识过程变得繁琐，且具有一定的局限性。此外，不同的激励水平往往会激发出具有明显差异的非线性恢复力，使得每一次实验都需要重复繁琐的选定过程，这也在一定程度上造成了人力与时间的耗费。

在进行系统辨识时，时域非线性子空间辨识方法通常需要已知响应和外载荷数据，但在某些情况下，外载荷是未知或难以测量的。准确了解结构系统所承受的真实外载荷特性，对于结构响应预测、设计优化及故障诊断等都具有重要意义［13-14］。因此，载荷识别问题受到了许多学者的关注，并已发展出多种辨识方法［15-18］。杨智春等［19］对动载荷的识别方法进行了述评，并介绍了神经网络在载荷识别中的应用。程光等［20］将一种改进的BP神经网络方法用于双跨转子系统的载荷识别，通过拾取实验信号进行预测证明了方法的有效性。然而，上述这些方法大多集中于处理与线性系统有关的载荷识别问题，但在实际工程中非线性系统更为普遍［21］，且由于非线性恢复力的存在，其载荷识别问题往往更为困难。

神经网络可以通过自适应训练过程来学习变量之间的关系，进而代替传统的机理建模［22］。经过大量数据训练后的神经网络模型可以等效代替响应-非线性恢复力映射关系，只需已知非线性位置的响应即可获得非线性恢复力，可有效避免重复繁琐的辨识过程。

因此，针对外载荷难以测量的情况，笔者旨在结合神经网络和子空间法对非线性系统载荷识别方法进行研究，并开展相应的数值与实验验证。

1 时域非线性子空间辨识方法

1.1 状态空间模型

对于一个包含h自由度的非线性时不变系统，其动力学方程可以表示为

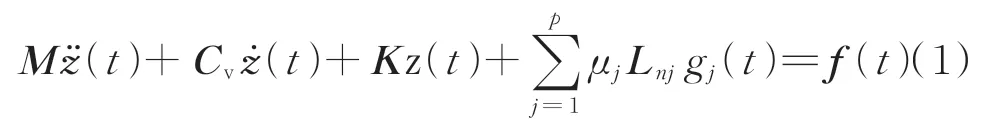
其中：M，Cv和K分别为质量、阻尼和刚度矩阵；下标v表示黏性；z(t)，(t)，(t)分别为连续时间t时刻的位移向量、速度向量和加速度向量；f(t)为载荷向量；非线性项由p个分量的总和构成；μj为非线性参数；gj(t)为非线性描述函数，代表非线性类型；Lnj为非线性元素的位置向量，通常Lnj中元素的取值为1，0或-1。

引入状态向量x(t)=[z(t)，z˙(t)]T，则式（1）的状态空间模型形式可以表示为

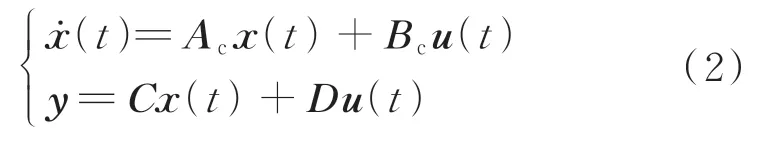
其中：u(t)=[f(t)，-g1(t)，…，-gp(t)]T为扩展输入向量；下标c表示连续时间。

1.2 时域非线性子空间辨识

在实际测量中，采样都是基于离散时间点的，故可以将式（2）描述的连续时间状态空间模型转换为离散时间状态空间模型

其中：k为时间序列；A，B，C和D分别为离散时间状态空间模型中的系统矩阵、输入矩阵、输出矩阵和反馈矩阵。

离散时间的系统矩阵和输入矩阵与连续时间的系统矩阵和输入矩阵的关系为

子空间方法的思想在于：通过未知的确定性系统生成测量数据总长度为s的输入向量和输出向量，利用线性代数工具辨识离散时间状态空间模型中的状态空间矩阵，一旦状态已知，辨识问题就成为了未知系统矩阵中的线性最小二乘问题［23］。实现状态空间矩阵的辨识首先需要确定扩展可观测矩阵Γi。通过对式（3）进行迭代，可得到

根据式（5），输入-输出矩阵方程可以写为

其中：下标p表示过去；f表示未来；块行数i由用户定义，应大于辨识系统的阶数n。

类似于未来的输入和输出，未来状态序列表示为Xf，状态序列定义为

式（6）中的扩展可观测矩阵Γi为

式（6）中的扩展下三角Toeplitz矩阵Hi为

将输入、输出数据收集到块Hankel矩阵中

当列数l满足l=s-2i+1时，意味着给定长度的数据可被充分利用。

根据式（10）和式（11），可将过去的输入、输出数据收集到块Hankel矩阵Wp=def[Up/Yp]。Yf的行空间沿着Uf的行空间在Wp的行空间上的斜投影可定义为ϑi

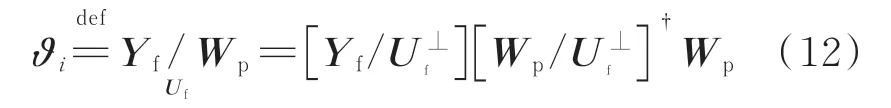
其中：符号‘⊥’表示正交补；‘†’表示广义逆［23］。

对加权斜投影进行奇异值分解

其中：W1和W2为用户定义的权重矩阵，W1需满秩，W2需遵循rank(Wp)=rank(WpW2)［23］。

当无噪声存在时，斜投影只有n个非零奇异值；当噪声存在时，则有n个以上非零奇异值。通过观察奇异值可以确定模型阶数n，进而确定U1和S1。可观测矩阵则通过得到。

系统矩阵A通过确定，输出矩阵C由Γi的前No行确定，No为输出的数量；输入矩阵B和反馈矩阵D则采用最小二乘求解以下线性方程组确定

在完成非线性系统的状态空间矩阵的估计后，可进一步计算扩展频响函数［6］，即

其中：HL=(K+iωCv-ω2M)-1为非线性系统中的标称线性频响函数；下标L表示标称线性；E表示扩展。

由式（15）可辨识得到标称频响函数及非线性参数。

2 基于神经网络的载荷识别

2.1 神经网络模型的训练

为解决时域非线性子空间辨识过程中非线性描述函数选定困难造成的辨识过程重复繁琐、计算耗时长等问题，本节旨在训练一个从非线性位置响应信号映射到非线性恢复力的神经网络模型，用以代替非线性描述函数的选定过程和时域非线性子空间辨识过程，如图1所示。

图1 神经网络模型等效代替辨识过程的示意图Fig.1 Schematic diagram of identification process equivalently represented by neural network models

针对非线性系统，基于大量数据对神经网络模型进行训练，网络的输入为非线性位置的响应，期望输出为时域非线性子空间辨识中采用三线性函数法重构的非线性恢复力，使用所需的网络层数、神经元个数、激活函数和训练算法等参数构建网络模型［19］，然后进行迭代训练，直到实际输出与期望输出之间的误差达到可接受的范围。训练数据越多且标定质量越好，训练后的神经网络模型表征能力越强，越能以高精度逼近复杂的输入-输出关系。若对结果精度有更高的要求，可以采取增加隐含层或神经元的数量，获得更大的训练数据集，尝试不同的训练算法等方式。

需要注意的是增加训练数据有助于提高神经网络模型的逼近精度，但付出的代价是网络模型可能会更加复杂，所需要的训练时间也更长。因此，在用神经网络模型等效描述响应-非线性恢复力映射关系时，通常需要在逼近精度和计算效率之间做适当折中。

2.2 载荷识别

根据非线性项视作反馈力的思想，式（1）可以写为

其中：fsum(t)为非线性恢复力fnl(t)与外载荷f(t)的合力，此时系统可看作是一个受合力的线性系统；下标nl表示非线性。

与式（6）同理，载荷识别模型可以写为

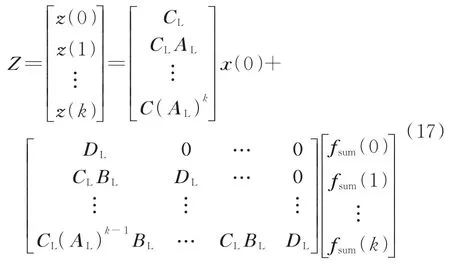
根据零初始条件x(0)=0，式（17）可以重写为

一旦获得标称线性系统状态空间矩阵AL，BL，CL和DL，就可以确定矩阵H，对式（18）进行最小二乘法估计，即可得到输入合力fsum(t)。

根据式（16）可以计算作用在系统上的外载荷为

由基于子空间法建立的载荷识别模型可知，非线性恢复力是识别非线性系统外载荷的关键。因此，利用训练后的神经网络模型预测非线性恢复力，可使非线性系统载荷识别得以实现。需要注意的是，本研究识别的载荷为时域的时间历程数据。

3 数值算例

间隙作为一种常见的非线性现象，广泛存在于工程结构中。间隙的存在会改变工程结构的动力学特性，进而导致动力学响应预测困难，甚至引发工程结构出现精度低、寿命短等问题。在系统辨识中，间隙相关非线性参数的确定是非常关键的，也是消除和控制间隙的必要条件［24］。对于间隙非线性系统来说，需要辨识的非线性参数包括间隙值和接触刚度。由于间隙值很小的误差就会导致接触刚度值出现较大的误差［24］，确定间隙值成为辨识间隙接触刚度的前提。本节以3自由度间隙非线性结构为例，说明所提方法的过程和性能。

3.1 3自由度间隙非线性结构

考虑一个3自由度间隙非线性结构，如图2所示，其动力学方程为

图2 3自由度间隙非线性结构的示意图Fig.2 Schematic diagram of a three degrees-of-freedom structure with clearance nonlinearity

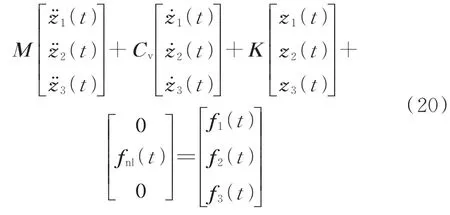
其中：M，Cv和K分别为3自由度结构的质量、阻尼和刚度矩阵；zh(t)，(t)和(t)分别为各自由度的位移、速度和加速度；fnl(t)为间隙非线性恢复力；fh(t)为各自由度的外载荷。

非线性恢复力可表示为

其中：kc为间隙接触刚度；dc为间隙值；z2为非线性位置的位移响应。

式（21）表示的间隙非线性的恢复力曲线如图3所示。

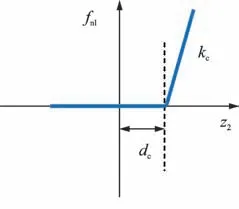
图3 间隙非线性的恢复力曲线Fig.3 Restoring force curve of clearance nonlinearity

该3自由间隙非线性结构系统的基本参数如表1所示。

表1 数值算例的系统参数Tab.1 System parameters of the numerical example

3.2 时域非线性子空间的系统辨识

对该结构的每个自由度各施加一个激励，选取的激励均为零均值高斯白噪声，即在任意两个不同时刻的采样信号均是统计独立的。利用Runge-Kutta方法数值仿真得到振动位移响应。仿真过程中，采样频率设置为1 kHz，采样时长为10 s，生成样本数据长度为104。以1组激励信号的均方根（root mean square，简称RMS）分别为39.445 4，40.178 3和39.839 8 N的仿真数据为例对辨识过程进行详细说明。

对于间隙非线性系统来说，间隙值的确定是辨识间隙接触刚度的前提。目前，已经发展了很多辨识间隙的方法，包括三线性函数法［6］、概率密度函数导数图法［24］和恢复力曲面法［25］等。笔者使用三线性函数法对间隙值进行辨识。根据仿真响应数据，将正位移范围［0，max（z（t））］划分为11个等距的间隔[dj-1，dj]。只有当测量的正位移超过用户定义的值时，每个非线性描述函数才有非零贡献。参考式（21），11个非线性恢复力可被定义为

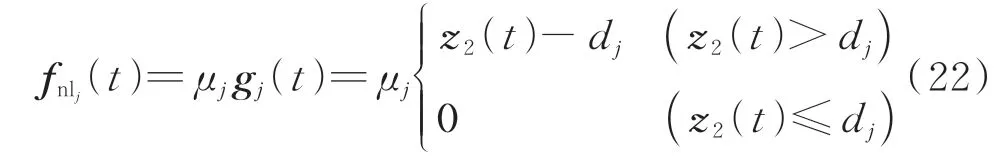
其中：dj为用户定义的间隙值；fnlj和μj分别为第j个非线性项的非线性恢复力和非线性参数。

利用时域非线性子空间辨识方法，可以分别得到每个非线性项中非线性恢复力的贡献和接触刚度的贡献，贡献较大且集中的区域即为间隙值附近。区间［0，max（z（t））］内的非线性恢复力和非线性参数分布如图4和图5所示。

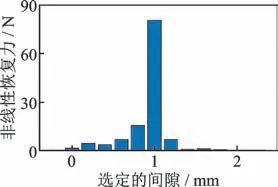
图4 区间[0,max(z(t))]内的非线性恢复力分布Fig.4 Distribution of nonlinear restoring force in[0,max(z(t))]

图5 区间[0,max(z(t))]内的非线性参数分布Fig.5 Distribution of nonlinear parameters in[0,max(z(t))]

为了得到更精确的间隙值，可以进一步缩小选定间隙范围为［0.8 mm，1.2 mm］，等距划分为4份，如图6和图7所示。从图中可以看出，间隙值主要集中在1 mm附近。图8给出了重构的非线性恢复力特性曲线与真实非线性恢复力特性曲线的对比。同时，该方法也可以辨识结构的状态空间矩阵，进而得到标称线性频响函数，如图9所示。

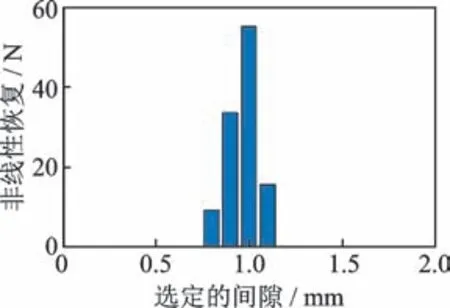
图6 区间[0.8 mm，1.2 mm]内的非线性恢复力分布Fig.6 Distribution of nonlinear restoring force in[0.8 mm，1.2 mm]

图7 区间[0.8 mm，1.2 mm]内的非线性参数分布Fig.7 Distribution of nonlinear parameters in[0.8 mm，1.2 mm]

图8 重构的非线性恢复力特性曲线与真实曲线Fig.8 The reconstructed and true nonlinear restoring force characteristic curve

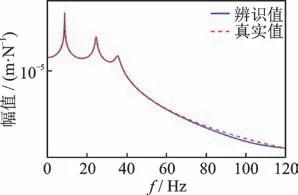
图9 辨识得到的标称线性频响函数H22曲线与真实曲线Fig.9 The identified and true nominal linear frequency response function H22 curve

结果表明，时域非线性子空间辨识方法可以获取准确的非线性参数值，然而过程较为繁琐，且每一次实验都需要重复上述辨识过程。

3.3 响应-非线性恢复力映射关系的神经网络模型训练

使用25组不同激励水平的载荷作用在结构上，利用时域非线性子空间辨识方法和三线性函数法重构对应的响应-非线性恢复力映射关系。用以训练的神经网络模型示意图如图10所示。

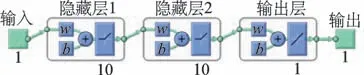
图10 响应-非线性恢复力映射关系的神经网络模型示意图Fig.10 Schematic diagram of the neural network models for nonlinear restoring force-response mapping relations

图10显示的神经网络模型含有2个隐含层，每个隐含层有10个神经元，使用Levenberg-Marquardt训练算法，图中w表示权重参数，b表示偏置参数。由于训练过程中使用的数据较少，且响应-非线性恢复力映射关系较为简单，在网络模型结构选取时，通过对多种不同层数、单元数及激活函数进行预实验以确定最优模型。从结果和计算效率的角度综合考虑，选择具有2个隐含层、每层10个神经元的神经网络模型进行训练即可达到较高精度。另外，反向传播训练算法Levenberg-Marquardt有利于梯度形式较简单的激活函数，且激活函数的梯度计算涉及到优化过程，结合间隙非线性特征，笔者选取Positive linear函数作为激活函数，其中输入为25组不同激励水平下的非线性位置响应，输出为时域非线性子空间辨识方法和三线性函数法重构的非线性恢复力。将输入-输出数据随机分成3个集合，其中70%用于训练，15%用于验证，15%用于完全独立的神经网络模型泛化测试。使用与上节系统辨识所用的相同仿真数据，通过训练后的神经网络模型进行预测，发现预测值与真实值吻合良好，如图11所示。

图11 神经网络模型预测的非线性恢复力特性曲线与真实曲线Fig.11 Predicted by neural network models and true nonlinear restoring force characteristic curve

结果表明，训练后的神经网络模型可以等效代替响应-非线性恢复力映射关系，即不论激励水平大小如何，只需已知非线性位置的响应即可获取非线性恢复力。

3.4 载荷识别

利用3.3节神经网络模型预测的非线性恢复力和测量的振动响应可以对非线性系统的外载荷进行识别。同样以激励信号RMS分别为39.445 4，40.178 3和39.839 8 N的仿真数据为例对识别过程进行详细说明。根据式（18）表示的基于子空间方法建立的载荷识别模型计算各自由度的合力，其中非线性位置的识别合力与真实合力对比结果如图12所示。图13为训练后的神经网络模型预测的非线性恢复力-时间关系。由式（19）可知，3自由度外载荷计算公式为

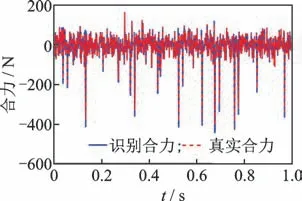
图12 非线性位置识别的合力与真实合力Fig.12 Identified and true resultant force at the nonlinear position

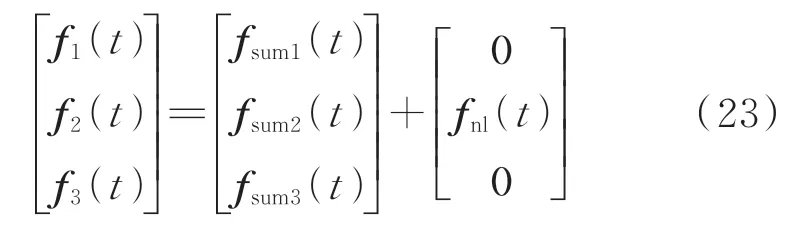
为了量化非线性系统载荷识别结果的精度，引入平均绝对误差评价指标（mean absolute error，简称MAE）

其中：q为数据总数量；f^为识别值；f为真实值。

结合图12和图13，可识别出非线性位置的外载荷与真实载荷，如图14所示，其MAE值为3.243 2。对于1，3自由度来说，由于没有非线性恢复力的存在，识别出的合力即为外载荷，以第1自由度载荷识别结果为例，如图15所示，其MAE值为1.274 4。结果表明，识别出的外载荷曲线与真实载荷曲线吻合良好，验证了所提载荷识别方法的有效性和可行性。

图13 神经网络模型预测的非线性恢复力与真实非线性恢复力Fig.13 Predicted by neural network models and true nonlinear restoring force

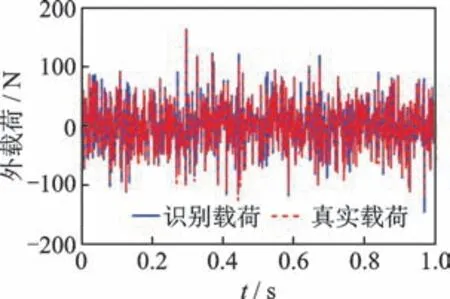
图14 非线性位置处识别的外载荷与真实载荷Fig.14 Identified and true external force at the nonlinear position

图15 第1自由度处识别的外载荷与真实载荷Fig.15 Identified and true external force at the first degree of freedom

4 实验验证

本节设计并搭建了1个3自由度间隙非线性实验结构，用于对所提出的载荷识别方法进行实验验证。图16和图17分别为3自由度间隙非线性实验结构的原理图和装置图。该结构由3个铝质质量块、4根薄梁以及钢质底座组成。由于铝块的质量相对较大，薄梁可以看作无质量弹性梁，质量块的水平位移只与竖直薄梁的抗弯刚度有关，因而所研究结构可视为3自由度振动系统。由于实际条件限制，无法在每个自由度施加激励，为识别非线性位置的外载荷，激振器作用在第2层。调节间隙大小的螺栓也设置在结构第2层。当激励足够大时，第2层铝块撞击到具有固定间隙的螺栓，从而产生非线性行为。激振器上布有力传感器用以测量实验中真实外载荷，同时利用3个电涡流传感器测量各层的位移响应，如图17所示。进行不同激励水平的实验，每次采集数据时长为10 s，采样频率为1 kHz。

图16 3自由度间隙非线性实验结构的原理图Fig.16 Schematic diagram of a three degrees-of-freedom experimental structure with clearance nonlinearity

图17 3自由度间隙非线性实验结构的装置图Fig.17 Set-up of the three degrees-of-freedom experimental structure with clearance nonlinearity

利用时域非线性子空间辨识方法重构的25组不同激励水平下的非线性恢复力数据以及测量的非线性位置位移响应数据，对图10所示的神经网络模型进行训练。使用RMS为4.190 0 N的白噪声随机激励作用在实验结构上，测量非线性位置响应，使用训练后的神经网络模型对非线性恢复力进行预测，发现预测结果与时域非线性子空间辨识结果几乎一致，如图18所示。图19给出了标称线性系统的频响函数辨识结果。

图18 神经网络模型预测的非线性恢复力特性曲线与重构曲线Fig.18 Predicted by neural network models and reconstructed nonlinear restoring force characteristic curve

图19 辨识得到的标称线性频响函数H22曲线Fig.19 The identified nominal linear frequency response function H22 curve

基于等效代替响应-非线性恢复力映射关系的神经网络模型和实测的振动位移响应数据对外载荷进行识别。图20为基于式（17）中载荷识别模型获取的非线性位置合力识别结果。图21为训练后的神经网络模型预测的非线性恢复力。结合图20和图21，根据式（23）可识别系统外载荷，如图22所示，其中蓝实线代表非线性位置的识别载荷，红虚线代表实际测量的外载荷，MAE值为1.879 0。两者趋势基本一致，吻合良好，进一步验证了所提载荷识别方法的有效性和可行性。

图20 非线性位置识别的合力Fig.20 Identified resultant force at the nonlinear position

图21 神经网络模型预测的非线性恢复力Fig.21 Nonlinear restoring force predicted by neural network models

图22 非线性位置识别的外载荷与实际测量的外载荷Fig.22 Identified and measured external force at the nonlinear position

5 结论

1）针对非线性描述函数选定困难，导致在不同激励水平下时域非线性子空间方法辨识过程重复繁琐的问题，采用多次重构的不同激励水平下的非线性恢复力数据和非线性位置响应数据对神经网络模型进行训练，用以等效代替响应-非线性恢复力映射关系。该方法避免了辨识过程对系统模型的依赖性，使得系统不论受到的激励水平大小如何，只需已知非线性位置的响应即可获得非线性恢复力，提高了计算效率。

2）针对外载荷难以测量的情况，利用训练后的响应-非线性恢复力神经网络映射模型预测非线性恢复力，提出了基于神经网络和子空间法的非线性系统载荷识别方法，并通过间隙非线性结构的数值与实验研究验证了所提载荷识别方法的有效性和可行性。

3）本研究仅基于间隙非线性系统对所提出的载荷识别方法进行了验证，但理论上该方法也适用于其他类型的非线性系统。