浅海波导界面对点源振速方向的影响∗
2015-10-27李家亮林建恒郭圣明衣雪娟
李家亮† 林建恒 郭圣明 衣雪娟
(1中国科学院声学研究所北海研究站 青岛 266023)(2中国科学院水声环境特性重点实验室 北京 100190)(3中国科学院大学 北京 100049)
⋄研究报告⋄
浅海波导界面对点源振速方向的影响∗
李家亮1,2,3†林建恒1郭圣明2衣雪娟1
(1中国科学院声学研究所北海研究站青岛266023)(2中国科学院水声环境特性重点实验室北京100190)(3中国科学院大学北京100049)
研究浅海波导对点源振速方向的影响具有十分重要的意义。采用“虚源法”分析计算了浅海波导环境中接收点处点源总振速方向与水平面夹角,侧重讨论确定性界面反射对总振速方向的影响。研究结果表明:总振速方向和接收点与声源的水平距离、两者深度,海底、海面特性以及声速剖面等有关。在等声速均匀浅海波导中,由于确定性界面反射的影响,当直达声掠射角为1°~50°时,合成总振速方向偏离直达声方向达1.5°~10.5°,声速剖面呈负梯度时,偏离程度更甚。
浅海波导,界面,虚源,质点振速
1 引言
海洋声场兼有标量场声压和矢量场振速,两者以不同的方式携带了声源和环境的信息。1978年,俄罗斯学者Shchurov[1]开始对海洋环境噪声矢量场进行了研究,探讨了相干分量和扩散分量之间的关系,组合接收系统的抗干扰能力等。Hawkes[2]等研究了宽带均匀各向同性噪声场中单矢量水听器各分量之间的噪声协方差。很多人对环境噪声场中声压与质点振速的相关性进行了研究,如:鄢锦等[3]针对浅海和均匀半无限空间环境,给出了计算噪声场中声压和质点振速空间相关的积分表达式;黄益旺等[4]在三维球面各向同性噪声模型下,研究了声压与质点振速间的相关性;尚华等[5]给出了噪声源在海面均匀分布时矢量水听器基阵阵元间的空间相关系数;杜敬林[6]等对浅海波导中声压与质点振速的垂直和水平分量的相关性进行了分析。哈尔滨工程大学的惠俊英[7]对浅海波导中简正波声强流及矢量信号处理进行了研究。可见人们对浅海波导环境声矢量场已进行一定研究并有所认识[1-9]。本文将采用“虚源法”研究浅海波导环境中点声源的振速场特性,分析声源以不同掠射角(即声源-接收点连线与水平面夹角)入射情形下的总振速场方向,侧重分析界面确定性反射情况下的点声源振速方向,讨论负声速梯度剖面对接收点总振速场方向的影响。
2 点源振速表达式
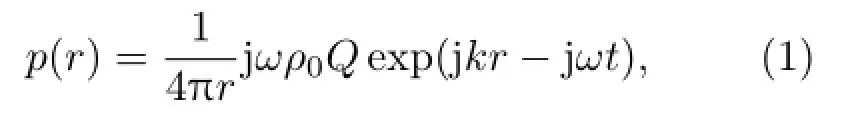
距点源r处振速
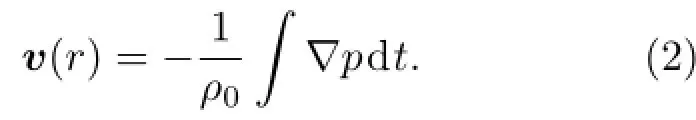
将(1)式代入(2)式,可得直达声传播方向(即接收-发射连线方向)上,距点源r米处质点的振速:
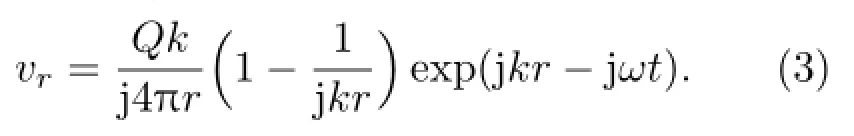
为计算方便,对于某一固定频率,暂且将(1)式和(3)式中的时间因子和常数项合并,分别简化为A 和B,则声压和振速分别为
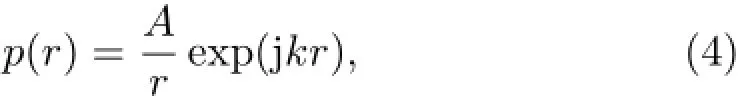

3 等声速情况下浅海波导中振速场
考虑等声速浅海波导环境,海面、海底的反射系数分别为V1和V2,海深h米。设单位强度简谐点声源位于海面以下z米处,接收点距离海面以下z0米,声源与接收点水平距离为r,接收器处声线的掠射角为θ,接收点、声源位置如图1所示。采用“虚源法”分析浅海波导多途效应对接收点振速方向的影响。
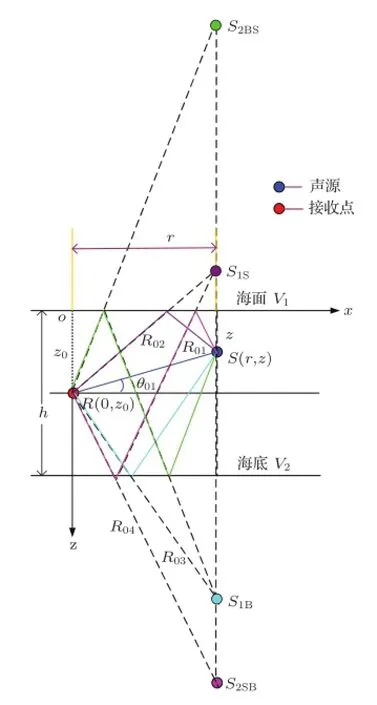
图1 等声速浅海波导中点源声场示意图Fig.1 Sound field of point source in shallow water waveguide with isovelocity profile
假设接收点R(0,z0)固定,点源位于s(r,z),考虑接收点处直达声、海面、海底一次和多次反射声的多途效应后,接收点处总声压为
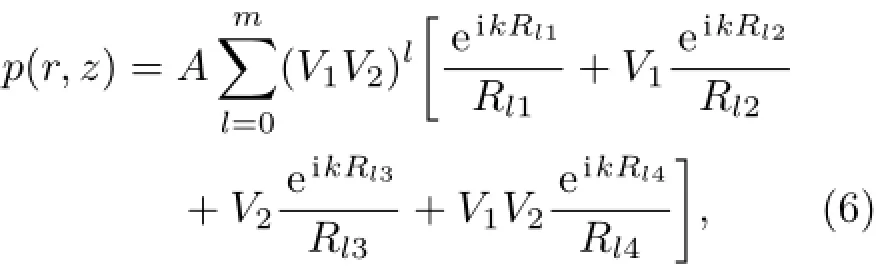
式中m为由界面反射构成的“虚源组”次数。Rl1,Rl2,Rl3,Rl4分别表示声源或虚源至接收点的距离:

当l=0时,R01,R02,R03,R04分别表示声源至接收点,海面一次反射、海底一次反射以及海面、海底各一次反射后虚源至接收点的距离。据此,由(6)式可获得接收点总声场振速表达式:

其中:Vln为总的界面反射系数,R为接收、发射连线方向单位矢量。接收点处总声场振速的x(水平)分量和z(垂直)分量分别为

振速垂直分量括号内后两项前的负号由坐标系决定,由此便可求得均匀浅海波导中接收点处声场的总振速方向与水平面的夹角γ:

应当指出,θ01是声源和接收点连线(均匀浅海中为直达声线)与水平面的夹角,它实际即为在接收点观察到声源在垂直面的真实方向。
4 数值计算
设单位强度简谐点源和接收点分别位于海面以下z=5 m和z0=30 m,下面计算接收点处总振速的方向γ(总振速方向与水平面的夹角)。计算过程中,接收点位置R(0,z0)固定,点声源深度保持不变,仅改变点声源到接收点的水平距离,也即改变声源点和接收点连线与水平面的夹角,即直达声线掠射角θ01。为了比较,对均匀半无穷海洋(没有海底)、等声速和声速负梯度浅海波导等三种情况的总振速方向进行对比分析,频率为200 Hz。
4.1均匀半无穷海洋(没有海底)
计算获得的总振速方向γ和直达声线掠射角θ01相比较如表1所示,仅有微小差距,这是因为近海面点源受到海面反射构成偶极子源而没有海底反射。
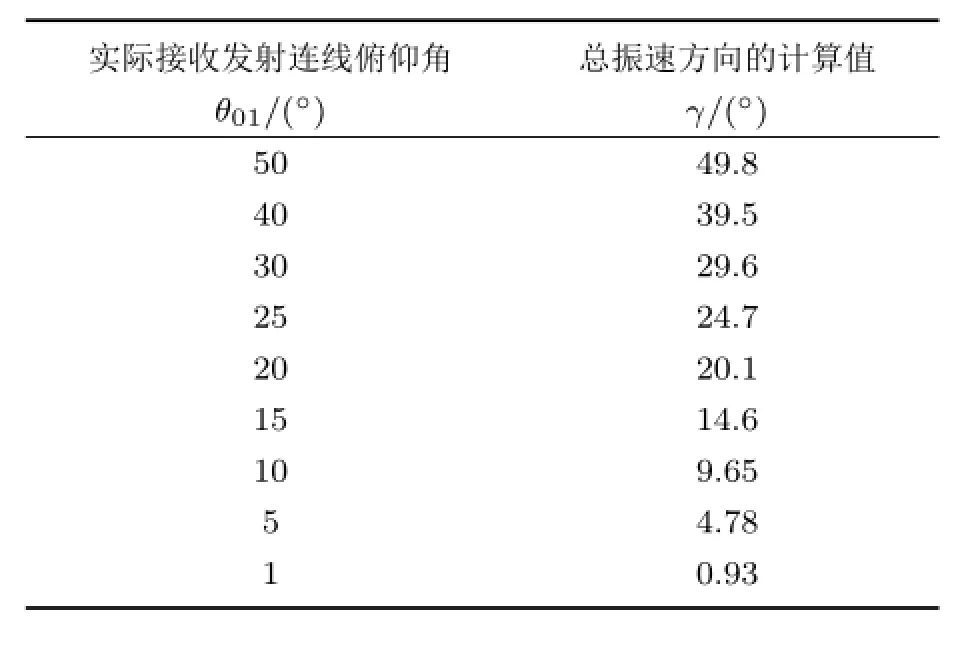
表1 总振速方向γ的计算值 (均匀半无穷海洋)Table 1The calculated direction of velocity γ (Uniform semi-infinite ocean)
4.2等声速均匀浅海波导
假设海深h=100 m,海面、海底的反射系数分别为V1=-1,V2=1,接收点和声源位置如上所述。以下数值计算结果表明,总振速方向的计算值γ与声源实际方向(接收-发射连线方向或直达声线掠射角)θ01相差很大,且计算值γ和“虚源组”次数m有关。表2是m=25、多种直达声线掠射角方向θ01情况下总振速方向γ的计算值。γ与θ01二者之差随入射角θ01的变化曲线见图2。由表2和图2可见,γ和θ01之差在1.5°~10.5°之间,表明浅海波导界面对总振速场方向有明显影响。
计算中发现,γ的计算值随m值增加逐渐趋于某一个固定值,图3给出了不同入射角θ01情况下的γ与m值的变化关系。

表2 总振速方向γ的计算值Table 2 The calculated direction of velocity γ
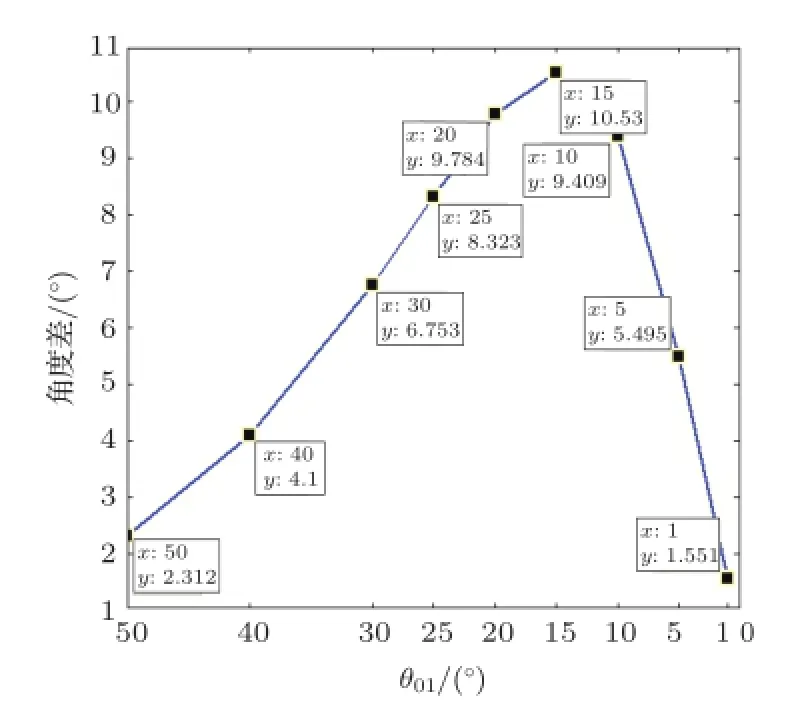
图2 γ与θ01二者差值随掠射角θ01的变化曲线(m=25)Fig.2 Difference between γ and θ01with different θ01(m=25)
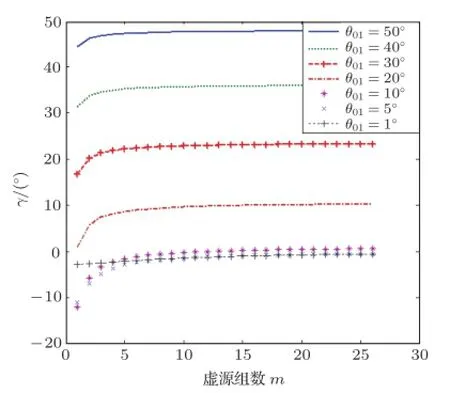
图3 γ计算值与界面反射“虚源组”次数m值的关系Fig.3 Relation between γ and m
由图3可见,当声源点和接收点连线与水平面的夹角,即直达声线掠射角θ01(入射角)大于5°时,“虚源组”次数m=10~20,总振速方向γ的计算结果会很快的趋向于某一个值,取更多的海底海面反射“虚源组”次数对计算结果没有太大影响。通常,m取5~10即可,且入射角度越大,达到一个稳定值需要的“虚源组”次数m越少。
据上述分析可以看出,由于近场时声源和接收点间距较小,直达声和前几次反射声起主要作用,因此虚源组数较少便可以使得总振速方向与水平面的夹角达到一个稳定值,这也是表2和图2中接收-发射连线与水平面夹角较大时计算得到的结果与实际结果相对较为接近的原因。
4.3声速负梯度浅海波导
假设海深100 m,声速剖面为负梯度,声速从海面到海底由1530 m/s变为1525 m/s,海底声速为1600 m/s,海底密度为1.2 g/cm3,海底声吸收系数为0.3 dB/λ,声源深度为5 m,接收点深度为30 m,接收点与声源水平距离为1432 m,接收点与声源连线与水平面夹角为1°,如图4所示。表3给出了7条声线在声源处的出射角、在接收点处的掠射角和声线的长度。
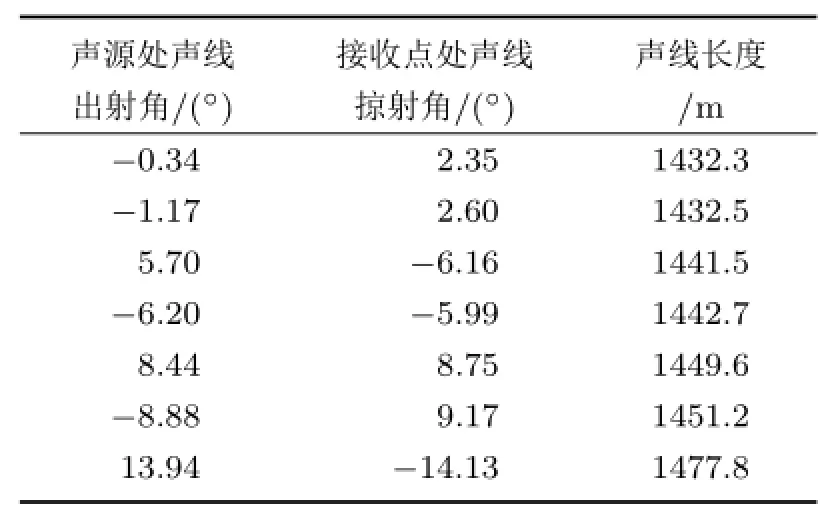
表3 声线传播数据Table 3 Data of rays propagation
根据公式(9)~(12)和表3计算得到,当声源和接收点连线与水平面夹角1°时,接收点处总振速方向与水平面的夹角为14°,两者差距较大。而由图3给出的均匀浅海波导情况下,声源和接收点连线与水平面夹角1°时的总振速方向约近0°。在浅海负梯度情况下,由于声线发生弯曲,使得接收点处直达声线方向已不能代表声源真实方向,加之界面对声线的反射影响,接收点总振速垂直方向偏离声源真实方向更大。在强负梯度情况下,对于某些水平距离处,甚至有的接收点会没有直达声,而接收点合成总振速的方向偏离声源真实方向即声源与接收点连线与水平面夹角方向可能会更大。
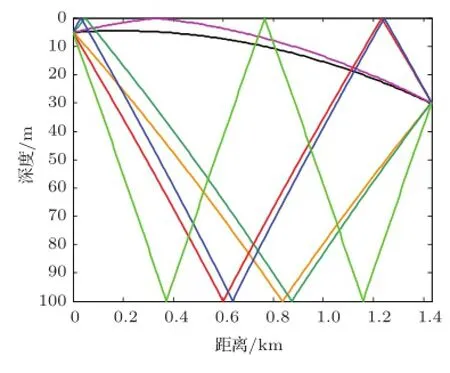
图4 浅海负梯度声线传播图Fig.4 Propagation of rays in shallow water with the negative gradient
5 讨论
(1)接收点和声源相对位置(上发下收,下发上收,收发同深)对γ计算结果的影响
为简单起见,仍以均匀浅海波导为例,在接收点和声源水平间距不变、接收点和声源上下相对位置变化(上发下收,下发上收)对总振速场方向的影响。图5是r=1432 m,接收点深度z0=30 m(靠近海面),声源分别位于接收点上方(z=5 m,θ01=-1°)和下方(z=55 m,θ01=1°)时,以及接收点深度z0=70 m(靠近海底),声源分别位于接收点上方(z=45 m,θ01=-1°)和下方(z=95 m,θ01=1°)时,计算的总振速方向γ与“虚源组”次数m的关系。图6与图5类似,仅将声源和接收点间距改为r=285.8 m,θ01=±5°,其余参数同图5。
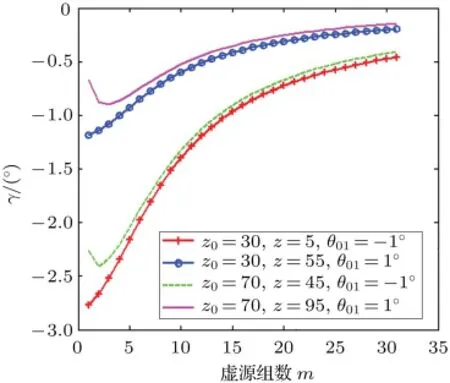
图5 r=1432 m,z0=30 m和70 m,θ01=±1°时,γ与m的关系Fig.5 Relationship between γ and θ01,r=1432 m,z0=30 m and 70 m, θ01=±1°
由图5和图6可以看出:1)对于直达声线掠射角小于等于5°的情况,不论接收点位于近海面或者近海底,也不论声源位于其上方或者下方,总振速方向的计算值γ随m的增加均由下方趋向于某一固定值;2)图5和图6对比可以看出,当θ01较大(声源和接收点连线与水平面夹角较大),即声源与接收点水平距离较近时,γ随m的增加趋于固定值的速度快于θ01较小、声源与接收点水平距离较远时的速度。
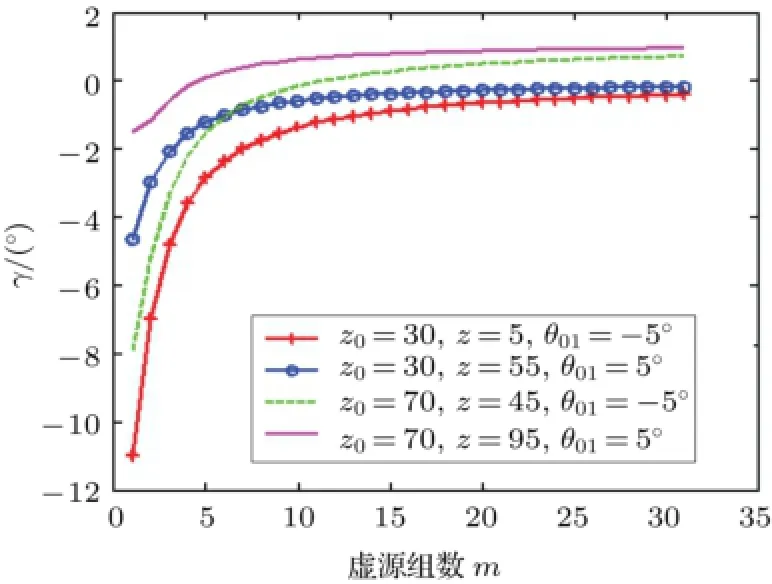
图6 r=285.8 m,z0=30 m和70 m,θ01=±5°时,γ与m的关系Fig.6 Relationship between γ and θ01,r= 285.8 m,z0=30 m and 70 m,θ01=±5°
(2)海底吸收对总振速场方向的影响
如果考虑海底吸收,海底的反射系数V2不为1时,总振速场方向的计算结果也会有所变化。仍以均匀浅海波导为例,取海底反射系数为0.8,此时总振速场方向的计算结果γ将更快的趋于某一固定值,如图7所示。

图7 γ计算值与界面反射“虚源组”次数m值的关系,V1=-1,V2=0.8Fig.7 Relation between γ and m,V1=-1,V2=0.8
当海底吸收较大时,海底反射的影响减弱,随着吸收系数的增加,逐渐接近于半无穷海洋的情况。
(3)浅海负跃层声剖面对总振速场方向的影响
对于浅海负跃层声剖面情况,不仅是界面,接收点和声源相对位置都将对总振速方向产生显著影响。此时,可以预料:跃层上发射和接收,海面和跃层对总振速方向影响大;跃层下发射和接收,海底和跃层对总振速方向影响大;当声源在负跃层上,接收点在负跃层下(上发下收)时,一般说来,相对于海面和海底,负跃层对总振速方向影响较大些;而声源在负跃层下,接收点在负跃层上(下发上收),对接收点振速方向有贡献的是那些能穿透跃层的声线。因此,在存在负跃层声速剖面的浅海中,界面和负跃层声速剖面对总振速方向的影响相当复杂。
上述结果表明,由于浅海波导界面反射和水中声速剖面引起的折射,形成声线弯曲,出现接收点总振速方向与声源与接收点连线方向有显著差别,这是均匀浅海波导中单纯利用总振速方向来判定声源在垂直面内的方向不准的主要原因。
6 结论
本文主要分析计算了浅海波导确定性界面反射情况下的垂直面内点源振速方向,并研究讨论了水中声速剖面对接收点振速方向的影响。分析和计算结果表明:
(1)半无穷均匀海洋没有海底反射,计算得到的总振速方向与水平面的夹角γ与声源-接收点连线方向相近,即声源真实方向或直达声的传播方向θ01(直达声线掠射角)相近,因此θ01可看作为总振速的方向,此时采用单矢量水听器测得的振速场(或声能流)方向可用于准确估计目标声源在垂直面的方向。
(2)在浅海波导环境中,由于海底、海面反射的影响,即使是等声速均匀浅海情况,接收点总振速场的垂直方向γ不再是声源真实方向或直达声传播方向θ01(直达声线掠射角)。负梯度声速剖面或负跃层声速剖面情况下,接收点总振速场的垂直方向偏离声源真实方向将会更大。因此,浅海中声速剖面分布引起的声线弯曲与界面镜像效应影响出现的单源变“多源”,是影响接收点合成总振速方向的主要原因。
(3)由于浅海中声速剖面分布引起的声线弯曲与界面镜像效应影响出现的单源变“多源”,接收点总振速的方向与直达声传播方向可能存在显著差异,因此,单纯用矢量水听器测得的合成总振速方向来表示声源在垂直面的方向,误差较大。
以上讨论未涉及浅海波导环境(包括界面和海水介质)随机性和环境噪声的影响,这将在后续工作中进行研究。
[1]SHCHUROV V.Vector acoustics of the ocean[M].Vladivostok:Dalnauka,2006.
[2]HAWKES M,NEHORAI A.Acoustic vector-sensor correlations in ambient noise[J].IEEE J.Oceanic Eng.,2001,26(3):337-347.
[3]鄢锦,罗显志,侯朝焕.海洋环境噪声场中声压和质点振速的空间相干[J].声学学报,2006,31(4):310-315.
YAN Jin,LUO Xianzhi,HOU Zhaohuan.Spatial coherences of the sound pressure and the particle velocity in underwater ambient noise[J].Acta Acustica,2006,31(4):310-315.
[4]黄益旺,杨士莪,朴胜春.体积噪声矢量场空间相关特性研究的一种方法[J].哈尔滨工程大学学报,2009,30(11):1209-1212. HUANG Yiwang,YANG Shie,PIAO Shengchun.Research on spatial correlation in an acoustic vector noise field[J].J.Hrbeu.,2009,30(11):1209-1212.
[5]尚华,黄益旺,张靖.基于矢量水听器的海洋环境噪声场空间相关[J].舰船科学技术,2009,31(10):43-46.
SHANG Hua,HUANG Yiwang,ZHANG Jing.Spatial correlation of ambient noise based on acoustic vector hydrophone[J].Ship Sci.Technol.,2009,31(10):43-46.
[6]杜敬林,迟寿育,马忠成.基于矢量水听器的浅海波导中海面噪声场的空间特性研究[J].舰船科学技术,2009,31(10):56-59. DU Jinglin,CHI Shouyu,MA Zhongcheng.Research on the spatial character of surface noise in shallow sea based on vector sensor[J].Ship Sci.Technol.,2009,31(10):56-59.
[7]惠俊英,惠娟.矢量声信号处理基础[M].北京:国防工业出版社,2009.
[8]孙贵青,杨德森,时胜国.基于矢量水听器的声压和质点振速的空间相关系数[J].声学学报,2003,28(6):509-513.
SUN Guiqing,YANG Desen,SHI Shengguo.Spatial correlation coefficients of acoustic pressure and particle velocity based on vector hydrophone[J].Acta Acustica,2003,28(6):509-513.
[9]孙岩松,李平,李风华.海面噪声场条件下声压与振速的空间互相关系数[J].海洋技术,2006,25(3):97-99.
SUN Yansong,LI Ping,LI Fenghua.Spatial crosscorrelation coefficients of acoustic pressure and particle velocity based on ambient noise field of sea surface[J].Sea Technol.,2006,25(3):97-99.
Effects of shallow water waveguide interface on the particle velocity direction from point sources
LI Jialiang1,2,3LIN Jianheng1GUO Shengming2YI Xuejuan1
(1 Qingdao Branch,Institute of Acoustics,Chinese Academy of Sciences,Qingdao 266023,China)
(2 Key Laboratory of Underwater Acoustic Environment,Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China)(3 University of Chinese Academy of Sciences,Beijing 100049,China)
It is very significant to study the effects of shallow water waveguide interface on the particle velocity direction from point source.In this paper,“Image source”method was adopted to analyze the direction of particle velocity and the horizontal angle of receiver point in shallow water waveguide,and the effects of certain interface reflection on the direction of particle velocity was studied.It is shown that:the direction of particle velocity has relationships with horizontal range and depth between source and receiver point,and the properties of surface and bottom and the sound speed profile.Because of the reflection of certain interface,the direction of particle velocity γ deviates from the incidence angle of direct sound as 1.5°~10.5°in the uniform sound speed in shallow water waveguide when the incidence angle varies from 1°to 50°,and the deviation can be more marked under negative gradient sound speed with isovelocity profile conditions.
Shallow water waveguide,Interface,Image source,Particle velocity
O422.2
A
1000-310X(2015)03-0249-06
10.11684/j.issn.1000-310X.2015.03.010
2014-05-09收稿;2014-05-23定稿
∗国家自然科学基金资助项目(11204345)
李家亮(1986-),男,山东人,博士研究生,研究方向:环境噪声。†
E-mail:lijiaqingdao001@163.com
