利用椭球约束求解区间平差模型的正则化方法

邓 伟，宋迎春，李文娜，谢雪梅

(1.中南大学 地球科学与信息物理学院，长沙 410083;2.中南林业科技大学 土木工程学院，长沙 410004)

在大地测量数据处理中，随着观测手段的增多，观测资料的累积，获取先验信息的可能性也越来越大，通过获取的先验信息建立约束条件一直是大地测量领域研究的热点。传统的最小二乘是基于残差平方和最小的方法，但是其平差结果在一些特殊情况下并不能够真实地表达出观测对象的物理或者力学性质。比如将不等式约束应用到大坝变形监测中，通过坡度方向和控制点的大致移动方向建立不等式约束条件进行解算，避免在无约束平差时两期平差值可能朝向任意方向的问题[1]。附加正确的、一定约束条件的平差模型，可以使平差结果在满足最小二乘准则的基础上，得到符合观测对象规律的更合适的解。在现代大地测量领域，运用较为广泛的就是等式约束[2-5]和不等式约束[1,6-8]，许多学者也对此进行了大量的研究并提出许多可靠的方法。

但是，在实际工程应用中，有许多用区间形式表达的参数约束信息。比如地球物理反演中的三维电阻率反演法，反演参数为电阻率，根据物理常识可以获得电阻率范围[9]。又如在大地测量参数反演中，反演参数岩土的密度值，由于密度是固有的正值，便能假设其大于零，且可以根据内部岩石特征得到参数值必定在某个区间内[10]。

针对参数带区间约束的平差模型，许多学者进行了各种算法研究。谢雪梅通过将平差问题转化为一个简单的二次规划问题，基于矩阵的正则分裂提出了一种迭代算法，并验证了该算法在系数矩阵病态情况下的有效性[11]；肖兆兵将区间约束转化为二次规划问题，基于Kuhn-Tucker条件，针对参数的不确定度提出了一种平差迭代算法[12]。夏玉国基于积极集思想，将最优化理论中的子空间截断牛顿法应用到测量平差中，有效改善了区间约束下平差模型的计算效率[13]。

带区间约束条件的最优化问题，有数学学者将区间约束条件转化成椭球约束条件进行求解[14]。即在区间约束周围外接一个椭球，扩大约束范围，利用椭球约束方法进行求解，将椭球特征矩阵的逆作为广义岭估计的岭参数。这种方法虽然可以解决区间约束最小二乘问题，遗憾的是解有时不在区间约束内。本文借助数学上的这类方法，提出一种改进的求解椭球约束的方法，通过对椭球特征矩阵进行加权，减小特征矩阵的半径来迭代求解，直至求出最优解。

1 区间约束最小二乘平差问题

带有区间约束的平差模型为：

L=AX+e，权阵为P，

s.t.α≤X≤β.

(1)

式中：s.t.是subject to的缩写，意思是“受约束”；A为m×n(m≥n)维系数矩阵;X=[x1,x2,…,xn]T为n维参数向量;L为m维线性化后观测值与近似值之间的差值;e为n维随机误差向量;α=[α1,α2,…,αn]T为参数下界;β=[β1,β2,…,βn]T为参数上界。

L=AX+e,

(2)

式(2)中，根据最小二乘平差准则VTPV=min，可以等价求解如下问题：

min(L-AX)TP(L-AX),

(3)

构造拉格朗日函数：

f(X)=(L-AX)TP(L-AX)+

(4)

分别对X和λ求导：

(5)

所以，

(6)

由于最优解Xλ都是在椭球面上取得，问题可以转变为求解在椭球面上的最小二乘问题。用传统的拉格朗日法求解式(6)的过程中，关键在于拉格朗日乘数λ的确定。文献[14]中不再将λ看作一个常数，而是看作依赖于样本的岭参数。通过式λ=XTATPL-XTATPAX对其进行迭代求解。文献[15]基于平衡损失函数，提出一种既考虑估计的精度，又考虑模型拟合优良程度的方法。

虽然将区间约束转化成椭球约束可以减少约束方程，便于加入平差模型进行求解，尤其是在待估参数向量维数比较高时，但是这是一种不对等的转换。为了便于从几何上来分析，以二维平面上的区间约束转换成椭球约束作为参考。如图1可以看出，将区间约束转化成椭球约束相当于在原本区间约束周围外接一个椭球。如果此时再使用传统的拉格朗日方法对椭球约束平差模型进行求解，可能会导致参数解虽然在椭球面上，但是不符合原本的区间约束条件。基于这个问题，文中提出一种新的求解椭球约束平差模型的方法，即将椭球约束条件作为一个惩罚项加入平差模型中，构造出一个新的辅助函数。惩罚项不断加权，按照一定步长减小约束椭球的半径，直至确定满足原始区间约束条件的解为止。

图1 区间约束区域与椭球约束区域比较

2 二次罚函数法

二次罚函数法是罚函数法的一种特殊形式[16]，惩罚项为约束条件的平方，优点在于比较简单、直观。对于等式约束最小二乘问题：

minf(x) s.t.ci(x)=0.

(7)

其中f(x)为目标函数；ci(x)=0为等式约束条件，式(7)的二次惩罚函数形式为：

(8)

其中，ρ>0为惩罚因子。二次惩罚法将违反每个约束的平方的倍数加到目标函数上，在ρ→∞的过程中，对约束条件的“惩罚”就越大，可以求解出一系列的无约束解。

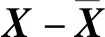
构造罚函数：

(9)

式中：μ为加权因子;Gμ为权矩阵，Gμ=μG，0≤μ≤1。通过式(9)可以看出，在μ变化的过程中，每一个椭球面上都可以求出一个在最小二乘准则下的解，但是要对该解进行判断，判断其是否满足区间约束条件。μ从1开始减小，直到确定不等式(3)的解为止。

F(X)=

(10)

求F(X)关于X的一阶导数并令其为0。

(11)

令二次罚函数法求得的解为：

(12)

二次罚函数法具体步骤：

1)利用先验信息确定参数上下界α和β。

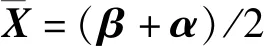
3)系数矩阵A，观测向量L，权矩阵P，初始惩罚项Gμ，μ=1作为输入项。

5)若对于Xqp中的所有元素，都满足α≤Xqp≤β(即参数值在约束区间之内)，则算法终止。

3 二次罚函数正则化

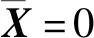
典型的正则化方法是Tikhonov正则化[17]，标准Tikhonov正则化的形式为：

(13)

式中：α为正则化参数。确定正则化参数的方法主要有L-曲线法[18]、广义交叉核实法(Generalized Cross-Validation，GCV)[19]和岭迹法[20]。鉴于广义交叉核实法适用性较弱和岭迹法选取的主观性太强的缺点。文中选择使用适用性强，并且能获得较为合理的正则化参数的L-曲线法来选取正则化参数。

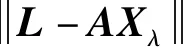
在二次罚函数法中引入正则化项，即：

minf(X)=

(14)

求f(X)关于X的一阶导数并令其为0。

(15)

(16)

对于参数带区间约束的平差模型，由于其双边不等式约束的特殊形式，直接求解可能比较麻烦。在计算时通常将其转化成椭球约束进行求解，变成在椭球面上求解最小二乘解的问题。针对椭球约束会弱化不等式约束，导致解可能不在区间约束内的缺点，文中提出的二次罚函数法可以很好解决这个问题。

当系数矩阵病态时，虽然椭球约束会对模型有一定的改善，但是这种改善太依赖于参数的先验信息。基于这样的缺点，文中提出在二次罚函数的基础上加入正则化项。既能通过约束条件使得最小二乘解满足观测对象的实际情况，又能更大限度解决系数矩阵病态带来的解不稳定的问题。

椭球约束正则化最小二乘法步骤：

1)利用先验信息确定参数上下界α和β。

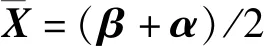
3)将系数矩阵A，观测向量L，权矩阵P，初始惩罚项Gμ作为输入项。

4)根据L-曲线法求出正则化参数α。

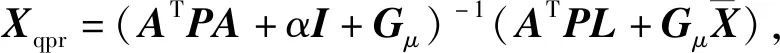
6)若对于Xqpr中的所有元素，都满足α≤Xqpr≤β(解算出的参数值在约束区间之内)，则算法终止。

4 算例与分析

在地球物理领域常常会遇到不适定问题，例如三维电阻率反演。其正演过程是基于有限差分或有限元一类计算方法的数值解，反演则是求数量巨大的各网格剖分单元电阻率值。反演需要求取的参数是各网格单元的电阻率值，而电阻率值是可以通过物理常识确定区间范围的，可以将约束范围条件加入平差模型进行解算[9]。

将非线性的三维电阻率反演问题线性化后，可以得到如下的反演方程：

AΔm=Δd.

式中，A为敏感度矩阵;Δm为模型参数增量向量;Δd为观测数据dobs与正演理论值dm的残差向量;dm是根据给定的模型参数由数值正演得到的理论观测值。三维电阻率反演问题往往表现为混定问题，导致方程为病态方程。

通常在模型中加入如下的不等式约束：

ρli≤mi≤ρui.

其中，mi为第i个网格的电阻率;ρli和ρui分别为第i个网格电阻率的下限和上限。对于ρli和ρui，可以根据物理常识来得到其变化的大致范围。

综合反演方程和不等式约束模型，可以得到如下的三维电阻率反演的目标函数：

F=min(Δd-AΔm)T(Δd-AΔm),

ρli≤mi≤ρui.

为了评价文中算法在大地测量反演中的效果，设计了如下算例进行验证。算例中用一个希尔伯特矩阵代替三维电阻率反演中线性化后的系数矩阵，真值假设为Xzhen=[1,2,3,4,5,6]T，假设根据常识得到的电阻率反演范围为：l=[0 0 0 0 0 0]T，u=[5 6 7 8 9 10]T，观测值L为根据系数矩阵和真值计算出来的观测值真值加上随机误差表示。A和L分别为：

L=AXzhen+e.

e为服从正态分布的随机数组成的向量，用其来模拟测绘实际工程中的观测误差。为了避免数据的特殊性，采用50次数值模拟实验，分别采取以下5种方案进行计算：

1)最小二乘法。

2)岭估计法(岭参数采用L-曲线法确定)。

3)奇异值分解法。

4)传统椭球约束法。

5)二次罚函数正则化法。

令最小二乘解为Xls，岭估计解Xre，截断奇异值分解的解为Xsvd，传统椭球约束的解为Xec，本文算法的解为Xqpr。

m1=(Xls-Xzhen)T(Xls-Xzhen),

m2=(Xre-Xzhen)T(Xre-Xzhen),

m3=(Xsvd-Xzhen)T(Xsvd-Xzhen),

m4=(Xec-Xzhen)T(Xec-Xzhen),

m5=(Xqpr-Xzhen)T(Xqpr-Xzhen).

m1，m2，m3，m4，m5分别代表每种方法求解出的参数偏离模拟真值的程度，结果如表1所示。

图2 最小二乘法计算结果

图3 岭估计法计算结果

图4 截断奇异值分解法计算结果

图5 传统椭球约束计算结果

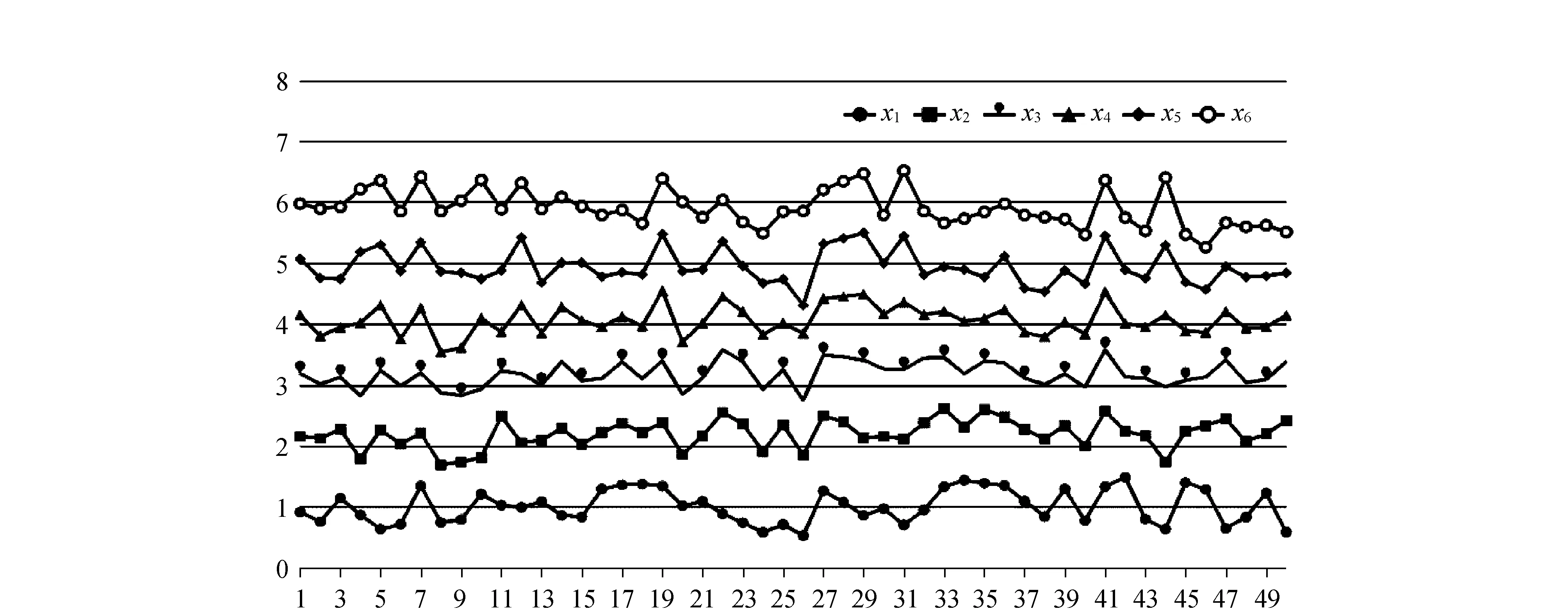
图6 文中算法计算结果

对模拟算例结果进行分析：

1)从表1可以看出，解偏离模拟真值的程度从大到小依次为：Xls>Xre>Xsvd>Xec>Xqpr。

2)设计矩阵A的条件数为1.495 1×108，属于严重病态矩阵。从图2可以看出，最小二乘解极不稳定，此时最小二乘解已经严重失真。

3) 岭估计法对于参数的估计精度太依赖于岭参数的选取，对模型的病态程度改善不够理想。解的稳定性相较于最小二乘法虽然有所改善，但是其只注重于降低病态性，没有考虑被观测对象的实际情况。

4) 截断奇异值分解法是通过去除设计矩阵接近于0的奇异值，通过损失待求参数的无偏性为代价来换取均方根误差的降低。解的偏离真值程度相较于最小二乘虽有所改善，但是依然很大，且解不稳定。

5) 利用参数先验信息，将其作为约束条件加入平差模型，可以极大提高解的稳定性。但是传统的椭球约束算法会出现解不在约束区间里面的情况，从图5可以看出，部分x1出现了小于0的情况。

6) 利用文中算法求出的解稳定性较好，不仅可以解决传统椭球约束算法的解可能不在区间内的缺点，而且通过加入正则化项，可以求得正则化参数与椭球特征矩阵逆的最优组合，更好地降低模型的病态性。

5 结束语

在大地测量数据处理领域，通过在平差模型中加入有效的先验信息作为约束条件，可以降低模型的不稳定性，提高解的精度和可靠性。文中在传统的椭球约束解算方法上，通过引入数学领域的二次罚函数法，对椭球特征矩阵进行加权，解决了传统椭球约束算法的解可能不在约束区间内的问题。传统椭球约束是以椭球特征矩阵的逆为岭参数的广义岭估计，文中在二次罚函数的目标函数中引入正则化项，选出正则化参数与椭球特征矩阵逆的最优组合。算例表明，文中算法在求解区间约束病态模型上有优势。

表1 解偏离真值的程度