同伦加权整体最小二乘平差算法
2022-11-04张重阳李成洪范小猛
张重阳,胡 川,李成洪,范小猛
(重庆交通大学 土木工程学院,重庆 400074)
整体最小二乘(total least squares,TLS)方法可以有效解决系数矩阵含有误差的参数估计问题,得到了学者的广泛关注。1980年,Golub和Van Loan从数值分析的角度用奇异值分解(singular value decomposition,SVD)方法得到了变量误差(error-in-variable,EIV)模型的TLS解[1],自此以后TLS法得到快速发展及广泛应用[2]。在测绘领域,通常会将TLS视作一个特殊的非线性问题,更多地是采用迭代解法进行TLS平差。Schaffrin[3-4]为解决异方差和结构EIV模型的参数估计问题,提出了加权整体最小二乘法(weighted total least squares,WTLS)。EIV模型在不同平差问题下具有不同的结构特征[5],部分变量误差(partial error in variable,PEIV)模型[6-7,8]能有效解决不同结构特征的EIV 模型参数估计问题。Fang[9]详细地研究了WTLS解存在的充要条件和随机参数估计问题,并阐述了不同迭代方法的异同。除此之外,也有研究人员从经典平差的角度出发,提出采用标准最小二乘法(standard least squares,SLS)来求解EIV模型,得到WTLS解算结果(即SLS-WTLS)[10],该法可直接利用间接平差的结果,有助于建立与经典平差的联系。WTLS迭代算法通常以加权最小二乘(weighted least squares,WLS)平差结果作为迭代初值,获得局部最优解,但当初值离WLS解较远时,迭代解法就存在法矩阵奇异和算法发散的问题。
为了解决此问题,Schaffrin等[3]在进行算法设计时,会预先计算一个近似WTLS解作为迭代初值,以确保算法具有良好的稳定性及收敛性。另一方面,同伦方法也能解决非线性模型的初值依赖问题[11]。连续同伦法[12]起源于延拓法,主要用于求解方程组[13-15],但早期尚未形成稳定有效算法。直到Li和Yorke提出预估-校正算法(Li-Yorke法)[16],让连续同伦法实现大范围局部收敛。同伦方法在大地测量领域已有一些相关研究,如陶本藻等[17]将同伦方法引入GPS伪距定位模型的LS平差计算之中,提高估计精度;张勤等[18]在理论上将同伦方法与WLS相结合,解决了WLS法的秩亏平差问题;游为等[19]将非线性同伦最小二乘模型应用于任意三维坐标转换,在初值离真值较远时获得了七参数的稳定解。前述研究的重点均在于非线性最小二乘(nonlinear least squares,NSL),为了解决初值对SLS-WTLS法收敛性影响的问题,进一步拓展EIV平差理论,文中以SLS-WTLS理论为媒介,采用同伦方法求解EIV模型,并提出同伦WTLS平差算法。
1 同伦WTLS
1.1 连续同伦方法及其解算
同伦来源于拓扑数学中的延拓概念,连续同伦方法是同伦方法中的一类,其算法是由Chow等提出的[15]。假设要求解的模型为y=F(x),为方程组yi=f(xi),(i=1,…,2,n)对应的向量值函数,同伦函数[19]可以定义为h(t,x)∈Rn+1:
(1)
其中

(2)

(3)
式中:B,G分别是F(X)的一阶(Jacobian matrix)和二阶偏导(Hessian matrix)矩阵。可以采用预估-校正法对式(3)进行解算,该算法具体实现过程可以参考文献[16]。
1.2 同伦WTLS平差模型及其解算
经研究,当以WLS解作为初值时,SLS-WTLS法能快速收敛并取得理想估计结果,但在初值精度较差的情况下,该算法会存在奇异和发散问题。为此文中引入同伦思想对该问题予以解决,一般的EIV函数模型可以表达为:
y+ey=(A+EA)ξ.
(4)
其中,y=(y1,y2,…,yn)T为观测向量,ξ=(ξ1,…,ξm)T为参数向量,A为n×m阶系数矩阵,ey与EA分别代表y与A中的偶然误差。
EIV随机模型表达为:
(5)
QA=Q0⊗Qx.
(6)

(7)
随机模型为:
(8)
由法方程得到的参数计算式为:
(9)
根据前述连续同伦方法对式(7)进行解算,首先按照标准最小二乘准则得到正交性条件方程为:
(10)
(11)
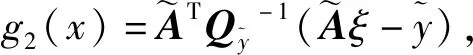
(12)
对式(12)求全微分,得到WTLS模型为:
(13)
进一步可以得到,
(14)
由式(13)计算切向量vk,即:
(15)
预估步长常用计算方法有欧拉预估法及四阶龙格-库塔(Runge-Kutta)法等[21],文中采用欧拉预估法。由式(16)可进一步得到预估值(tk+1,ξk+1),即:
(tk+1,ξk+1)=(tk,ξk)+Δt·vk.
(16)

(H(tk+1,ξk+1)).
(17)
根据预估-校正法的原理,对同伦解曲线λ(s)=(t(s),ξ(s))进行跟踪,从t=0和ξ=ξ0端点开始,直到t=1且g2(ξ*)=0,解ξ*即为求得的参数估计值。外符合精度加权残差平方和(TSSR)及内符合精度验后单位权方差计算式为:
(18)
(19)
根据SLS理论,参数估计值的协因数阵为:
(20)

(21)
2 同伦WTLS平差算法
根据同伦方法的基本原理,推导得到同伦WTLS平差计算式,为了得到稳定有效的结果,算法流程设计如下:
输入观测向量,系数矩阵A及对应的权阵Px,Py。
1)初始化:确定初始点(t(0),ξ(0))=(0,ξLS),并给定步长Δt与阈值ε1=10-7、ε2=10-5,ε3取值与步长有关,k=0。
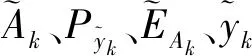
3)校正:按式(17)以(tk+1,ξk+1)为初始值,采用牛顿迭代法得到tk+1参数校正序列{ξk+1(i)},i=1,2,…。为了与算法计算次数k有所区分,以i值代表牛顿迭代计算次数。牛顿迭代的终止条件[22]为:
(22)
4)检验:判断tk+1,若|tk+1-1|<ε3,输出ξk+1*并以式(18)~式(21)进行精度评定,否则以(tk+1,ξk+1(i))为初始值,转至步骤(2)。
3 实验分析
为了验证所提算法的可行性,评估同伦加权整体最小二乘算法的性能,本节以直线拟合和平面坐标变换问题为例进行讨论。
3.1 直线拟合
直线坐标数据来源于文献[23],对应的权值来源于文献[24]。为了方便比较,文中将文献[9]的算法简称为Fang-WTLS,并将其与同伦WTLS法分别对前述直线数据进行拟合,3种方法的参数估计结果见表1。

表1 同伦加权整体最小二乘算法参数估计结果
经研究计算发现,文献[3,10,25]所提算法的计算结果与Fang-WTLS法相一致。根据表1可知,在步长选取恰当的条件下,新算法能够得到可靠稳定的结果,与Fang-WTLS法保持一致,由此可见,同伦WTLS法具有可行性。另一方面,随着步长的减小,同伦解曲线的零点数量在逐渐增加,其收敛速度亦随之减小。
在此基础之上,针对SLS-WTLS算法自身存奇异及发散问题进一步研究。为此通过不断增大新初值与WLS解的距离‖Δξ0‖=‖ξ0-ξWLS‖,对比两种算法的收敛性,表2列出了两种算法收敛性差异。

表2 两种算法收敛性比较
当‖Δξ0‖逐渐增大时,SLS-WTLS法在进行迭代的过程中出现了法方程奇异问题和发散问题,而同伦WTLS算法在步长取0.000 01时估计结果稳定收敛并且精度可达mm级以上。
综上所述,同伦WTLS法具有可行性,在步长选取恰当的条件下,得到的结果与Fang-WTLS法相一致。在初值离真值较远时,新算法仍能够得到稳定收敛解。
3.2 二维坐标变换
二维坐标变换问题的核心是确定目标坐标和原坐标系之间变换的参数。算例的实验数据来源于文献[26],在步长分别取0.1、0.01和0.001时采用同伦WTLS法得到4项参数估计结果及精度列于表3。
根据表3可知,Δt取0.001时,平面坐标变换的参数估计结果及精度指标相对于WLS法来说,更符合实际的情况,再次证明了同伦WTLS算法的可行性。图1描绘了各项参数估计结果随步长取值变化情况。
从图1可知,当步长较大时,收敛速度较慢,t接近0.8左右时曲线才接近平缓,这是由于误差累积造成的。而步长取0.001时解曲线在t接近0.1时就接近收敛状态,最终结果与Fang-WTLS法的估计结果及精度指标相一致。
为了进一步验证新算法的收敛性及稳定性,在初值取值不同的情况下,采用同伦WTLS与SLS-WTLS法参数估计结果及精度见表4。
根据表4可知,就坐标转换问题而言,当初始距真值较远时,SLS-WTLS法在迭代时会存在矩阵计算奇异而不收敛,由此导致最终结果不准确或是计算失败。二维坐标转换算例结果表明同伦WTLS法具有良好的收敛性,这与前述直线拟合算例是一致的。

表3 二维坐标变换问题的同伦WTLS法参数估计结果

表4 不同初值下两种算法平面坐标变换参数估计值
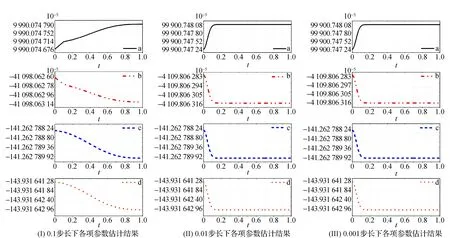
图1 不同步长取值对应坐标变换各项参数估计结果
4 结束语
文中以SLS-WTLS迭代解法存在的初值问题为出发点,将同伦方法与加权整体最小二乘法相结合,提出一种用于线性EIV模型参数估计新方法。
1)在步长选取适当的条件下,同伦WTLS方法估计结果能与其他WTLS算法保持一致,新算法具有可行性。
2)同伦WTLS算法具有大范围收敛的性质,解决了SLS-WTLS法在近似值距真值较远时存在法矩阵奇异和算法发散问题。
3)参数估计及精度与步长取值有着较为密切的关系,选取恰当的步长,参数估计精度就越高,结果也就越可靠。
