大地线极点归化纬度的迭代求解法

李 鑫，姚德新，金立新

(1.兰州交通大学 测绘与地理信息学院，兰州 730070；2.地理国情监测技术应用国家地方联合工程研究中心，兰州 730070；3.甘肃省地理国情监测工程实验室，兰州 730070；4.中铁第一勘察设计院集团有限公司，西安 710043；5.甘肃铁道综合工程勘察院有限公司,兰州 730000；6.海军工程大学，武汉 430043)

对大地线的研究在椭球大地测量学中是非常重要的内容，它是经典大地主题解算基础。目前国外学者对大地线的研究主要方向为克莱劳定理，利用其他方法对其重新论证、对广义克莱劳方程研究等方面，国内学者目前研究方向主要是解决疆域确定等诸多需要绘制大地线的问题[1]，文中主要研究大地线极点归化纬度的求解问题。早期白塞尔提出一种需要复杂迭代计算的解算长距离大地问题的公式，但当时没有电子计算机，所以解算起来十分复杂繁琐，因此国内外许多学者都致力于非迭代解法的研究，赫尔默特在正解中消除了迭代；索达诺等研究了反解的非迭代计算；纪兵借助Mathemaica代数系统进行了重新推导，得到了形式简单、便于实用的正反解直接解形式[2]。文中主要研究基于白塞尔方程的大地线极点归化纬度求解，为大地主题正反算提供一种新的思路。白塞尔微分方程将大地线映射变形为平面曲线、将大地线映射变形为椭圆弧。性质是保持归化纬度、大地线方位角、类归化纬度不变。深入研究发现，两个白塞尔微分方程有规律性、关联性，有内在的本质联系，都可以表达为归化纬度的函数，也可以表达为大地纬度的函数，同样可以表达为类归化纬度即球面弧长的函数。在当前椭球大地测量学研究中，以白塞尔微分方程为基础所表达的系列函数来研究大地线新的映射拓扑性质，对当前大地线的理论研究有很关键的承接作用，并且求解大地线极点归化纬度后，可以直接计算大地主题反解中大地正反方位角，因此以白塞尔微分方程表达的系列函数为基础，对大地线极点纬度进行求解十分必要。

1 克莱劳定理正弦表达

由文献[3]可知大地线长度S与大地经度L、大地纬度B、大地方位角A的一阶微分关系式为：

(1)

式中：N为卯酉圈曲率半径;M为子午圈曲率半径[4-6],根据式(1)可得克莱劳方程[3]：

r·sinA=C.

(2)

式中：r为平行圈半径，根据文献[7],可将式(2)改变形式得到新形式：

(3)

式中：u为归化纬度，un为此条大地线上最高点的归化纬度。其计算方法使用克氏方程[7]。

(4)

2 重要定义推导

为得出大地线极点归化纬度迭代式，首先必须推演得出白塞尔球面弧长和球面经差的具体表达，此表达式要以归化纬度u为自变量且包含大地线极点归化纬度un。结合二者的表达式可以推演以归化纬度为自变量的椭球面和白塞尔球面经度之差的具体表达式，进一步可以得到迭代式。

2.1 白塞尔球面弧长

在单位圆球面上易知大圆弧微分方程[8]：

du=cosαdσ.

(5)

式中：u为归化纬度;α为球面方位角;σ为球面弧长。根据白塞尔投影条件，大地线和大圆弧上相应点的方位角相等，则式(5)可写为：

du=cosAdσ.

(6)

由式(3)克莱劳定理易得：

(7)

对式(6)求积分可得到球面弧长的归化纬度表达式为：

(8)

2.2 白塞尔球面经差(归化经度)

在单位圆球面上易知大圆弧微分方程[8]：

(9)

式中：ω为球面经差。同理，根据白塞尔投影条件，大地线和大圆弧上相应点的方位角相等，则式(9)可写为：

(10)

式(10)结合式(3)则可得出：

(11)

将式(8)推演得到的球面弧长的归化纬度表达形式代入式(11)，对其求积分可得球面经差的归化纬度表达式为：

(12)

式(12)推演过程如下：

(13)

证毕。

3 白塞尔球面直角三角形定理

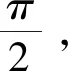
(14)

根据上述数值，得到白塞尔球面直角三角形示意图如图1所示，图中N为球面极点；u0为球面赤道；大地线上三点的投影点位分别为：P0(u0,ω0)，Pi(ui,ωi)和Pn(un,ωn)，各点位之间和极点之间球面弧长均在图1表示。

图1 白塞尔球面大地线元素示意图

结合图1，根据球面直角三角形Napier通用规则[9]可得：

(15)

结合三角函数对式(15)进行形式变换，则可得到式(3)、式(8)和式(12)，对于其克莱劳定理正弦形式、球面弧长和球面经差的归化纬度表达式的正确性得到验证，并且由此可知，大地线投影的球面弧长σ和球面经差ω从大地线升交点起算。

4 经度缩量

经度缩量是指大地线在椭球面和白塞尔球面上的经度差异。由文献[10]，白塞尔微分方程中椭球面上经差L与白塞尔球面上经差ω微分关系式为：

(16)

结合式(11)，则白塞尔经差微分方程变换为：

(17)

式(17)即为大地线经差与归化纬度、球面弧长的微分关系式。对式(17)求积分，将其等式右边级数展开：

(18)

式(18)中e为椭圆第一偏心率[11]，又根据式(8)归化纬度和球面弧长的关系可得：

(19)

结合(18)、(19)两式并且整理形式后，式(17)可得到如下表达：

(20)

对式(20)第一项求积分可得：

(21)

积分过程如式(22)。

(22)

式(20)后三项中正弦函数部分通过倍角函数公式转化一次幂余弦函数：

(23)

结合上文推演，对式(20)求积分得：

(24)

将式(24)整理可得：

(25)

将式(25)简写：

(26)

式(26)中：

k2=

(27)

其中c=cosun。

式(26)进一步可写为；

(28)

式(28)中l为经度之差，且式中ϖ具体表达式为：

(29)

式(28)中等式右边第二项为经度缩量，定义为ε，具体表达式为：

(30)

(31)

一个基本弧长的归化经度，亦即极点un的椭球面经差(归化经度)定义为ln，具体表达式为：

(32)

基本弧长的椭球面经差(归化经度)小于90°，亦即经度有缩量，称为经度缩量。经度缩量大小取决于两个元素，即偏心率和大地线极点纬度。大地线经差(归化经度)从大地线升交点起算。大地线升交点至极点的经差为一个基本弧长的归化经度。大地线升交点经度加上两个基本弧长的归化经度等于大地线降交点经度。

5 大地线极点归化纬度求解

利用(8)、(12)两式，或者白塞尔球面直角三角形的Napier法则，可得球面经差余弦表达：

(33)

根据上文，结合式(33)，则可得到：

cosΔσ12=

sinu2sinu1+cosu2cosu1cos(Δl12+Δε12).

(34)

结合上文，证明过程如下：

cos(σ2-σ1)=cosσ2cosσ1+sinσ2sinσ1=

cosu2cosu1cosω2cosω1+cosu2cosu1sinω2sinω1+

sinu2sinu1=cosu2cosu1cos(ω2-ω1)+sinu2sinu1=

sinu2sinu1+cosu2cosu1cosΔω12，

(35)

证毕。

同理结合式(33)亦可得：

(36)

式(36)中：

Δω12=Δl12+Δε12.

(37)

其中Δε12是椭球面和白塞尔球面经度差之差，定义为经度缩量之差。结合经度缩量部分的内容，经过形式变换，得到经度缩量之差的表达式为：

(38)

结合上部分内容，若大地线上的两点不跨越大地线极点，则此大地线上两点各元素如图2所示：l1,l2和ln分别是大地线上点1、2和此大地线极点的大地经度与此大地线升交点大地经度L0之间的经度之差。

图2 两点不跨越大地线极点示意图

根据式(34)、式(36)、式(37)，则迭代式确定为：

(39)

又因为Δε12是微小量，故初值可选定为：

(40)

(39)、(40)两式即为大地线极点的归化纬度计算式。

6 算例分析

大地线极点归化纬度最直接的应用是大地坐标方位角的求解，为验证大地线极点归化纬度正确性，根据大地线长短，选取短距离(100 000 m以内)和超长距离(5 000 000 m～10 000 000 m以内)的大地线进行正反大地方位角的求解，并且将求解结果与传统大地主题反算得到的正反大地方位角对比，从而验证大地线极点归化纬度的正确性。

首先利用短距离大地线进行计算，已知大地线上起点和终点的大地坐标分别为：

(41)

选择克拉索夫斯基椭球参数，按照白塞尔大地主题解算方法反算可得大地线长度和正反大地方位角为：

(42)

然后利用大地线极点的归化纬度求解正反大地方位角，首先根据式(40)求出大地线极点归化纬度的迭代初值，计算初值所需数据和初值计算结果如表1所示。

表1中W为辅助函数，表达式为[12]：

(43)

式中：椭球第一偏心率e和白塞尔大地主题反算一致，均采用克拉索夫斯基椭球参数。

结合辅助函数，由文献[3]，可得到大地纬度B和归化纬度u的关系式为：

(44)

由式(44)可得表1中两点归化纬度的正弦和余弦值，结合表中所有数据，得到迭代初值。

得到迭代初值后，将初值代入式(39)，利用Wolfram Mathematica编程，进行迭代计算，迭代结果如表2所示。

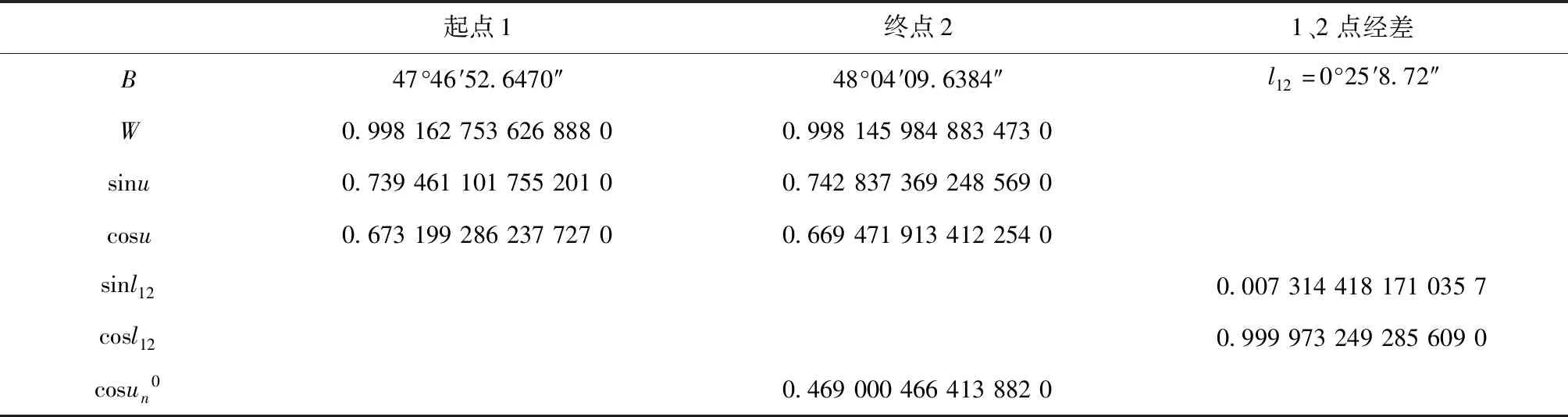
表1 大地线极点归化纬度的迭代初值

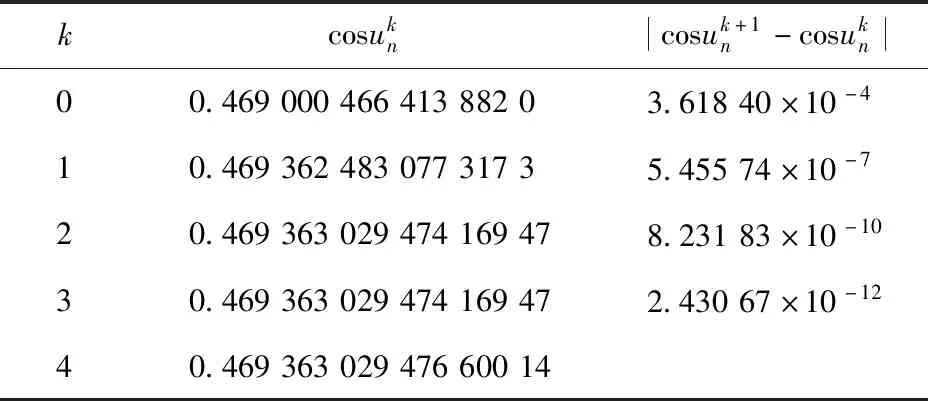
表2 大地线极点归化纬度的迭代结果

由表中迭代计算结果可以看出迭代计算4次，精度已经足够高，用第4次迭代结果结合表1数据，代入式(3)得：

(45)

根据式(45)，可得此大地线正反方位角为：

(46)

式(46)结果与式(42)白塞尔大地主题解算结果一致，大地线极点归化纬度求解正确，说明短距离适用。接下来对长距离进行验证，与短距离同理，已知大地线上起点和终点的大地坐标分别为：

(47)

同理，选择克拉索夫斯基椭球参数，按照白塞尔大地主题解算方法反算可得大地线长度和正反大地方位角为：

(48)

与短距离计算极点归化纬度过程相同，过程数据和迭代初值计算结果如表3所示。

表3各数据计算方法与表1同理，得到迭代初值后，结合式(39)，利用Wolfram Mathematica编程，进行迭代计算，迭代结果如表4所示。

表3 大地线极点归化纬度的迭代初值

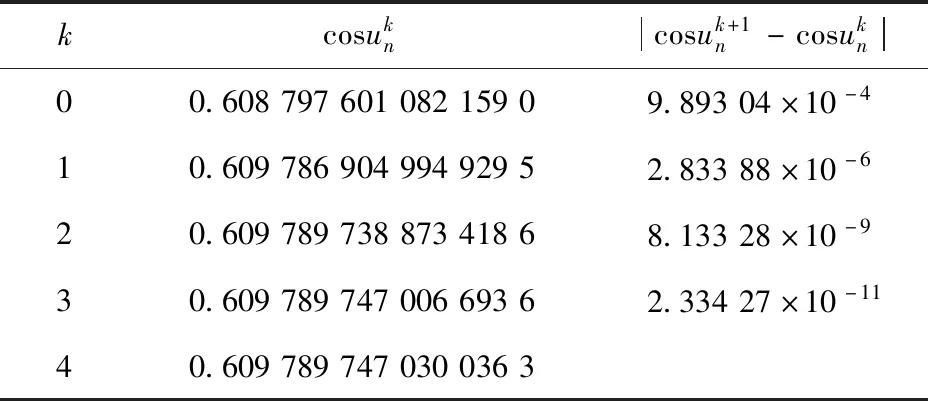
表4 大地线极点归化纬度的迭代结果

与短距离迭代结果类似，收敛速度快，再次印证公式合理性。同理，利用第四次迭代结果计算可得：

(49)

根据式(49)，利用反正弦函数计算结果后化为度分秒，结合象限判断，可以得到大地线正反方位角为：

(50)

式中结果与式(48)白塞尔大地主题解算结果相同，证明大地线极点归化纬度求解正确，说明长距离适用。

7 结束语

利用大地线克莱劳定理和白塞尔微分方程推演得到了大地线在椭球面和白塞尔球面经差的函数关系式，得到两球面之间经度缩量之差的具体表达式，最后结合三角函数巧妙地分离了大地线流动点和最高点的归化纬度，得到大地线极点归化纬度的迭代求解式，代入实际数据计算迭代结果，将其运用在大地主题反算中大地线短距离(不跨越赤道)和长距离(跨越赤道)正反方位角的求解，验证了大地线极点归化纬度迭代求解法的可靠性。在椭球测量学中，根据已知大地线极点归化纬度，可为大地主题直接解算提供新思路，并且在大地线新的理论研究中，大地线映射拓扑所构建的新型椭球的定位等问题也需要求出大地线极点的归化纬度，因此在目前大地线新的理论研究中，大地线极点的归化纬度求解有着承上启下的重要意义。