如何理解“小数除以整数”的算理

□余千

学生在学习“小数除以整数”时，理解小数除以整数的本质“计数单位再细分”是理解的难点。如何帮助学生理解“小数除以整数”的算理，教师可以采用如下教学环节。

一、多元表征，初步理解算理

1.创设情境。教师出示生活情境：小明妈妈在微信群中发了11.5元的红包，微信群有5名成员，平均每人能分到多少元？让学生独立尝试做题。

2.展示交流。学生汇报各种方法，教师板书。主要有以下三种方法。

方法①：11.5×10=115（角），115÷5=23（角），23÷10=2.3（元）。

方法②：10÷5=2（元），1.5÷5=0.3（元），2+0.3=2.3（元）。

方法③：竖式计算（如图1）。

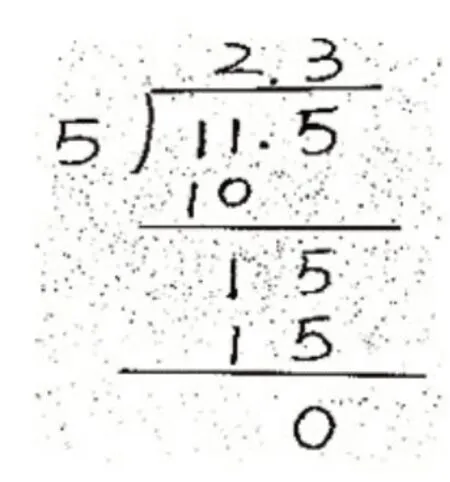
图1

3.重点讨论。教师引导学生讨论方法②中的“1.5÷5”为什么等于0.3元？启发学生思考：1.5元平均分给5个人，先把1元换成10个1角，5角换成5个1角，共15角，平均分给5个人，每人分得3角，即0.3元。教师课件演示过程，如图2。

图2

4.联系理解。教师提问：你能用这样的方法说明图1中的方法③吗？竖式中的“15”怎么来的？表示什么意思？商的小数点为什么写在2的后面？商中的“3”又表示什么意思呢？在教师的引导中，学生理解小数除法的每一步算理。

5.师生小结：当元不够平均分的时候，我们只能把它化成更小的单位“角”来继续平均分。也就是说，当大的计数单位不够平均分，需要转化成更小的计数单位来继续平均分。

二、对比沟通，深入理解算理

1.比较方法之间的联系。教师同时呈现三种方法，引导学生两两比较方法之间联系。通过比较让学生感受到方法①和方法②是通过现实情境（元与角之间进率转换），把小数除法转化成整数除法。方法③是直接通过变换计数单位，把小数除法转化成整数除法。这三种方法从本质上来说是一样的。

2.理解竖式的写法。教师呈现图3中的竖式，启发学生：竖式中的15是由1个一转化成10个0.1，再加上5个0.1得到的，表示的是15个0.1。当余数不够平均分时，需要把大的计数单位转化成小的计数单位，把小数除法转化成整数除法。

图3

三、拓展延伸，内化算理

1.教师呈现学习单（如图4），学生独立解答。

图4

2.全班交流，重点讨论剩下的钱如何继续平均分（如图5）。

图5

教师提问：竖式中的“80”怎么来的？表示什么意思？商中的“5”又表示什么意思呢？

通过多元表征，沟通算理和算法之间的联系，并适度的拓展延伸，可以使知识得到转化和迁移，从而帮助学生更好地理解小数除以整数的算理，提高学生的思维能力。