如何理解“乘法分配律”

□张小燕

如何帮助学生更好地理解乘法分配律，可以设计以下教学活动。

一、计算比赛，激活经验

1.教师出示以下一组题目，要求学生比一比，谁算得又对又快。

6×7+4×7 78×14+22×14

2.师生反馈交流，请算得又对又快的学生与大家分享计算方法。

6×7+4×7 78×14+22×14

=（6+4）×7 =（78+22）×14

=10×7 =100×14

=70 =1400

教师提问：为什么可以这样计算？你能解释其中的道理吗？

二、自主探究，解释算理

1.教师出示活动要求：用你喜欢的方式解释道理，可以用文字、画图、举例等方法。如果有困难，可以借助信封里的学具（信封里有点子图和长方形图）。

2.先让学生独立思考，再四人小组交流。

3.全班交流。选择用不同方法的作品，展示学生的说理过程。

方法（1）：根据乘法的意义，6个7加4个7，就是10个7。

方法（2）：举例说明，如一个面包7元，男生有6人，女生有4人，每人买一个面包，一共花了多少元？可以先分别算出男生和女生各花了多少元，再求一共多少元，算式为6×7+4×7；也可以先算出一共有多少人，再求一共多少元，算式为（6+4）×7。

方法（3）：用点子图来说明（如图1）。

图1

方法（4）：用长方形面积模型来说明。可以先分别算出两个小长方形的面积，再相加；也可以拼在一起算出大长方形的面积（如图2）。

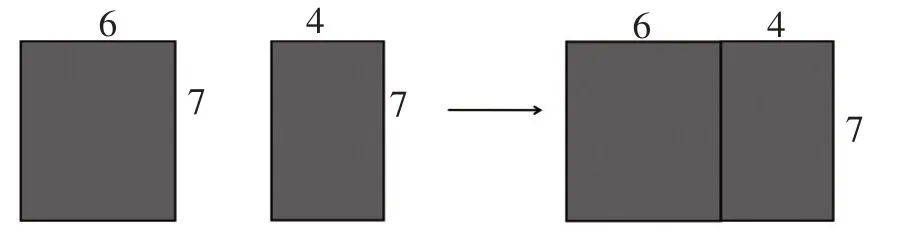
图2

4.分析比较，构建基本模型。

（1）沟通联系，教师提问：这些方法有什么相同的地方？

全班通过讨论得出，这些方法虽然思考的角度不同，但都说明了一个相同的道理：几个几加几个几，就是一共（几+几）个几。

（2）比较讨论，教师提问：把6×7+4×7变成（6+4）×7，变的是什么？不变的又是什么？

学生总结：把6×7+4×7写成（6+4）×7，变的是外形和运算顺序，不变的是本质和计算结果。

（3）举例并概括规律。让学生每人举几个这样的例子，如97×25+3×25=（97＋3）×25……

教师提问：你能用一个算式表示大家举的例子吗？引导学生建立基本模型：ɑ×c+b×c=（ɑ+b)×c或（ɑ+b)×c=ɑ×c+b×c

三、运用知识，应用模型

1.学生独立解答：李大爷家有一块菜地（如图3），这块菜地的面积有多少平方米？

图3

2.教师出示下列算式，要求学生观察数据特征，判断哪道题运用乘法分配律合适？为什么？

①（25+14）×4④13×15+7×15⑦27×98②（15+45）×3⑤14×78+22×14⑧99×78+33×66③125×（80+8）⑥27×102

上述活动，从不同角度帮助学生理解乘法分配律的本质，有效建构了乘法分配律的模型。