水平井岩屑流量预测模型研究及应用

王学强，王翔，雷银，陈轶林，徐煜

1.中国石油西南油气田分公司工程技术监督中心（四川 成都 610051）2.中国石油西南油气田分公司工程技术处（四川 成都 610051）

0 引言

由于岩屑床和掉块导致的井眼不清洁造成钻头泥包、井壁坍塌、卡钻、漏失等复杂钻井事故是影响钻井施工过程中安全和效率的主要问题[1-3]。现场一般是根据岩屑返出情况来评价井眼清洁，因此，在钻井过程中连续、实时、准确地计量返出岩屑流量，对于降低钻井事故、提高钻井效率非常重要[4-5]。

通过文献查阅，目前岩屑返出的监测手段主要有以下几种：专家经验、井下工程短节与地面岩屑称重装置[6]。依靠专家经验通过分析返出岩屑的形状、大小和数量以及起下钻过程中钻柱移动是否顺畅来评价井眼清洁情况，但该方法无法实时获得岩屑返出信息，且专家经验太过主观，所以该方法对井眼清洁监测效果不好。井下工程短节测量环空压力，再根据环空压力计算环空岩屑浓度以分析井眼清洁情况，但该方法井下工具成本高，不利于大范围推广。在振动筛出料口安装岩屑称重装置，实时对岩屑流量计量，该方法是目前最普遍采用的，肖敬涛等提出了无线岩屑流量测量装置及应用[7]；曾永文等提出了岩屑体积平衡计算方法与分析流程来进行水平井的井眼清洁分析[8]，但他们都未考虑当岩屑称重装置发生仪器失效或者数据包丢失造成数据不完整、不连续的问题。

为解决岩屑称重装置发生仪器失效或者采集数据包丢失的问题，研究分析了岩屑称重计量原理，建立了3种岩屑流量计量预测模型，实现了对岩屑称重采样周期内的岩屑数据进行预测，解决了由于岩屑称重装置仪器失效或者数据包造成的数据丢失问题，对实时监测井眼清洁，优化分析钻井时效，减少非生产时间的产生有重要意义。

1 岩屑流量计量原理

岩屑流量计量系统总体设计方案如图1所示。岩屑流量计量系统由综合录井仪、岩屑称重装置及岩屑称重上位机组成[9-10]。

图1 岩屑流量计量系统总体设计

1）综合录井仪。综合录井仪主要由传感器、快速色谱、数据采集模块、计算机系统与数据库组成[11]。

综合录井仪主要作用是为岩屑流量计量系统提供井号、井深、日期、时间、钻压、大钩负荷、转速、转盘扭矩、出入口流量等数据。

2）岩屑称重装置（图2）。岩屑称重装置主要功能是完成钻井随钻岩屑的采集、计量、倾倒、挂扫、称重等功能[12]。岩屑称重装置包含可编程逻辑控制器、称重传感器、位置传感器、压力传感器等各类传感器和气缸执行机构。可编程逻辑控制器除了完成钻井随钻岩屑的采集、计量、倾倒、挂扫、称重等功能外，还要把采集到的数据通过相应的通讯端口送到上位机。

图2 岩屑称重装置

3）岩屑称重上位机。岩屑称重上位机的主要功能是控制岩屑称重装置，将岩屑称重装置采集的数据结合综合录井仪数据进行计算，分析存储并实时化曲线显示理论与实际的瞬时、整米、立柱岩屑流量[13]，同时需要做到与岩屑称重装置、综合录井仪同步通讯。

虽然上述钻井岩屑流量计量系统能实时计量返出岩屑质量流量，但因现场恶劣的工作环境及其他因素，岩屑称重装置会发生失效或者采集数据丢失，这些故障会造成数据不完整，进而影响井眼清洁情况的评价。岩屑流量预测模型就是对岩屑称重装置采集周期内某点数据进行预测，解决岩屑称重装置故障导致数据不完整的问题。

2 岩屑流量预测模型建立

针对岩屑流量计量装置故障导致岩屑流量数据不完整、不连续的问题，研究了3种岩屑流量计量预测模型，分别为多项式拟合模型、最小二乘法线性拟合模型以及BP神经网络模型。

2.1 多项式预测模型

岩屑计量装置共采集了位于计量周期里的N个钻井随钻岩屑的质量数据，每个数据由x和y两个变量组成。变量x表示记录钻井随钻岩屑质量时的时间间隔；y表示钻井随钻岩屑的质量。用( )xi,yi来表示数据中的一个点，i=1，2，3，…，N。

多项式预测模型：

将(xi,yi)代入式（1）式可得：

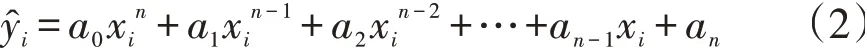
用误差平方和来表征所有的ŷi与样本点yi的偏差，记为

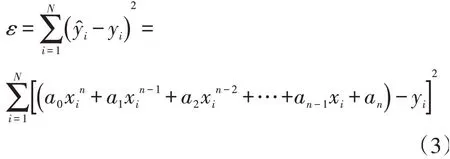
使ε最小的aj(j=0,1,…,n)即为最佳拟合系数，将（3）式对aj(j=0,1,…,n)求偏导并令偏导等于0得

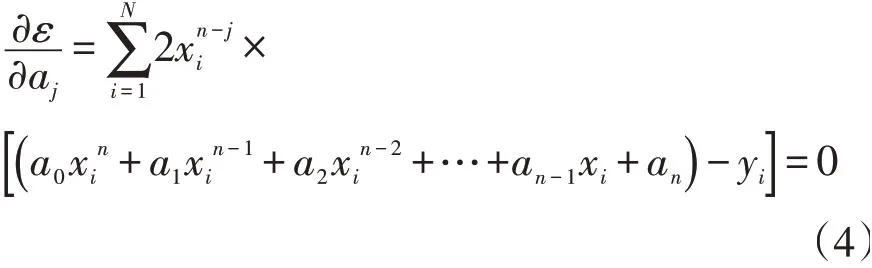
根据式（4）可解得一组拟合系数aj(j=0,1,L,n)使得ε最小，这组拟合系数即为最佳拟合系数。

2.2 最小二乘法线性预测模型

岩屑计量装置共采集了位于计量周期里的N个钻井随钻岩屑的质量数据，每个数据由x和y两个变量组成。变量x表示记录钻井随钻岩屑质量时的时间间隔；y表示钻井随钻岩屑的质量。用（xi,yi）i=1,2,3,L,N来表示数据中的一个点。

钻井随钻岩屑流量计量最小二乘法线性预测模型的计算方法：

根据平方损失函数定义，平方损失函数的计算方法为：

把式（5）代入式（6），得：

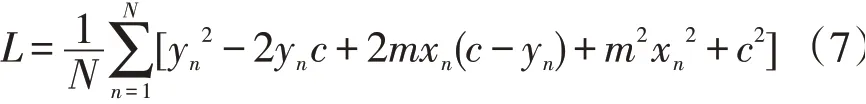
对式（7）的变量c和m分别求偏导数：

则：

把（11）式和（12）式带入（5）式，则：

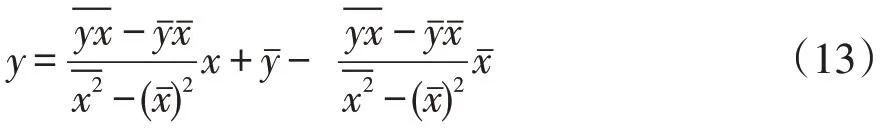
2.3 BP神经网络预测模型

BP神经网络是一种信息正向传播，误差反向传播的反向传播神经网络。通常由输入层、隐含层、输出层3层构成。BP神经网络计算包含两个阶段，第一阶段是信息正向传播，输入信息从输入层经过隐含层处理传到输出层得到预测输出，然后权衡预测输出与期望输出之间的误差。预测输出与期望L输出之间的误差未达到预期精度则进入第二阶段误差反向传播，误差信息从输出层反向传播至输入层来调整输入层到隐含层以及隐含层到输出层的权重和阈值。重复以上阶段，直至误差达到预期精度，如图3所示。

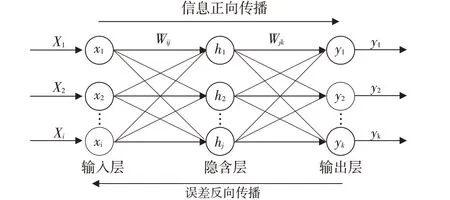
图3 典型3层BP神经网络模型

1）信息正向传播阶段。设节点i和节点j之间的权值为ωij，节点j的阀值为bj，每个节点的输出值为yj，而每个节点的输出值是根据上层所有节点的输出值、当前节点与上一层所有节点的权值和当前节点的阀值还有激活函数来实现的。具体计算方法如下：

其中f(x)为激活函数，一般选取S型函数或者线性函数。在BP神经网络中，输入层节点没有阀值。

2）误差反向传播阶段。设输出层的预测输出为dj，期望输出为yj，损失函数取均方误差函数如下：

根据梯度下降法，权值矢量的修正正比于当前位置上E(ω,b)的梯度，对于第j个输出节点有：

假设激活函数f选择，则：

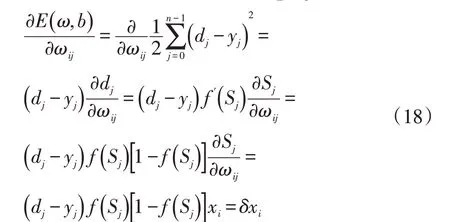
根据梯度下降法，结合式(18)、(19)，对于权值和阀值调整如下：

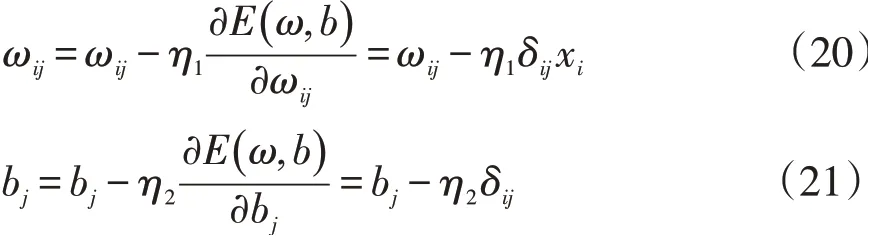
3 岩屑流量预测模型仿真研究

岩屑计量装置共采集了位于计量周期里的106组钻井随钻岩屑的质量数据，分别用3种岩屑流量计量预测模型进行分析仿真，并计算3种模型的性能指标。

3.1 多项式预测模型仿真

多项式预测模型仿真结果如图4所示。其中，均方误差为0.565 8，相关系数为0.989 8；最大误差为1.956 0，最小误差为0.002 2，分别出现在第89、40组数据处，误差分布曲线如图5所示。

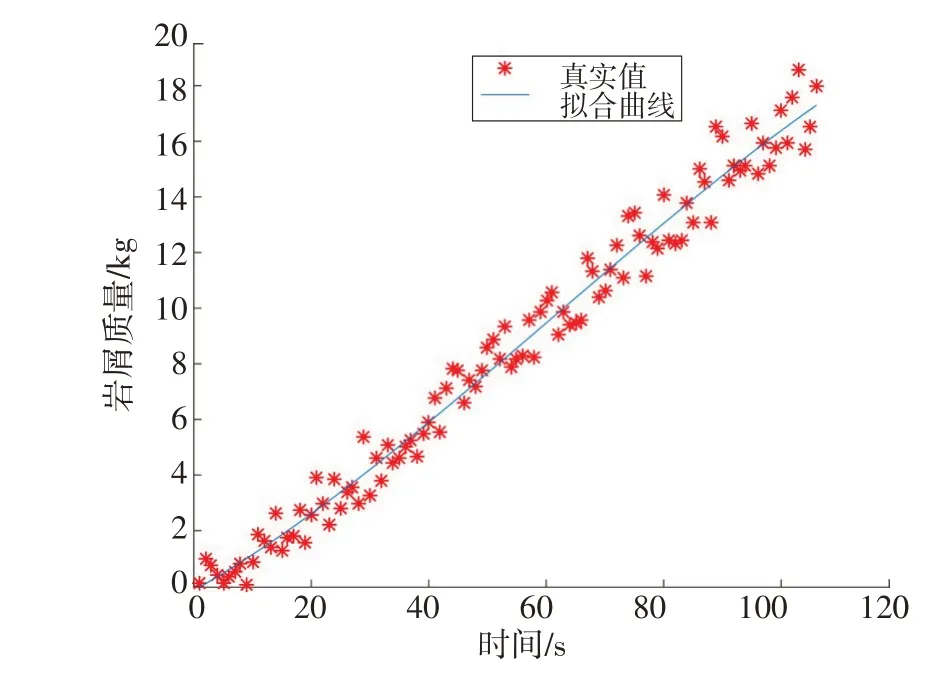
图4 多项式预测模型仿真结果

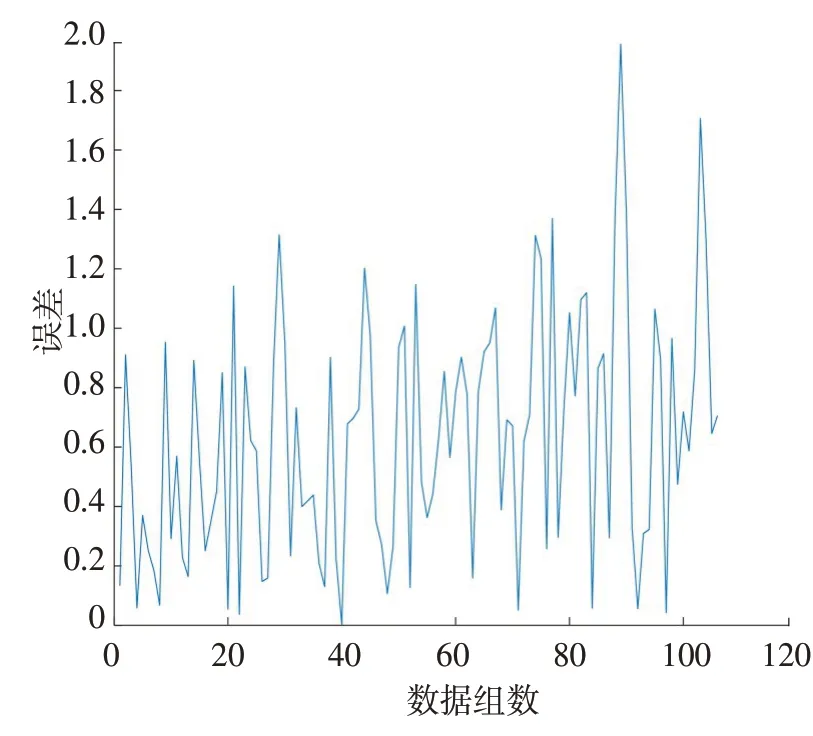
图5 多项式预测模型误差分布曲线

3.2 最小二乘法线性拟合模型仿真

最小二乘法线性预测模型拟合结果如图6所示。其中，均方误差为0.591 3，相关系数为0.989 4；最大误差为2.077 7，最小误差为0.000 8，分别出现在第89、52组数据处，误差分布曲线如图7所示。

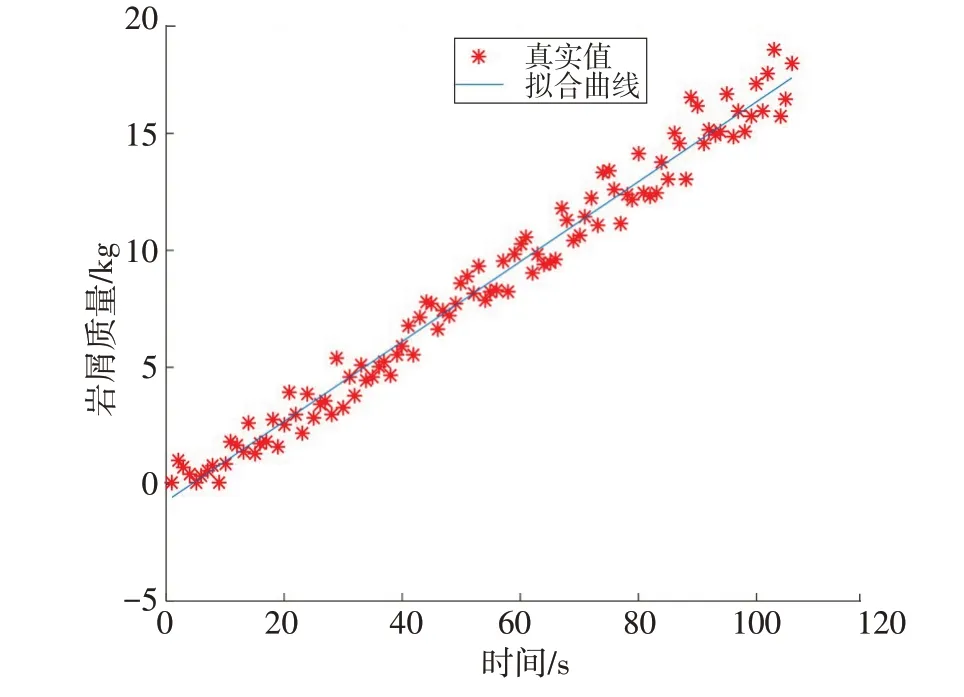
图6 最小二乘法线性拟合模型仿真结果

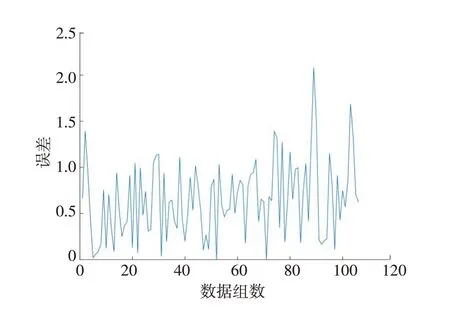
图7 最小二乘法线性拟合模型误差分布曲线

3.3 BP神经网络模型仿真

BP神经网络仿真结果如图8所示。其中，均方误差为0.448 0，相关系数为0.991 9；最大误差为1.728 0，最小误差为0.010 2，分别出现在第88、71组数据处，误差分布曲线如图9所示。

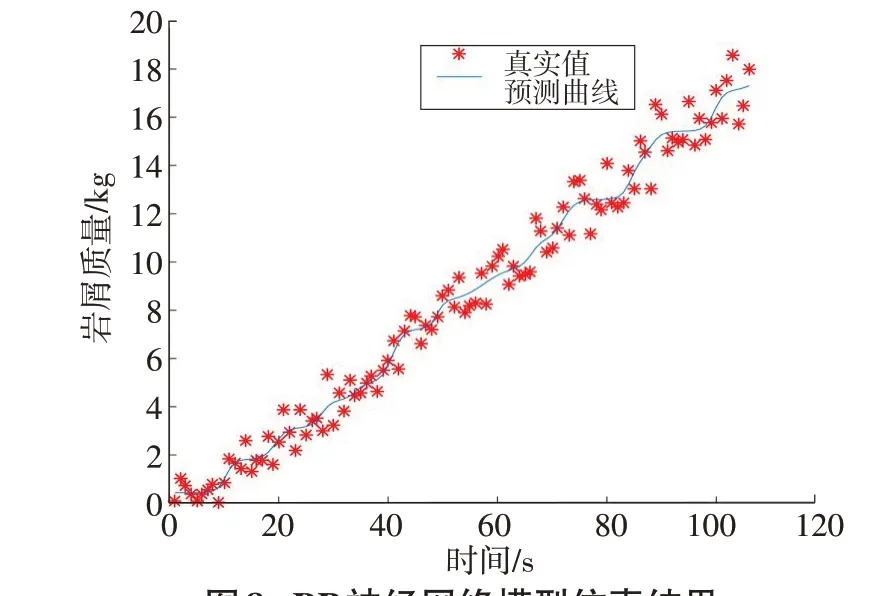
图8 BP神经网络模型仿真结果

图9 BP神经网络模型误差分布曲线

综合图4至图9以及表1，BP神经网络模型对岩屑计量的拟合以及预测是3种模型中效果最好的。

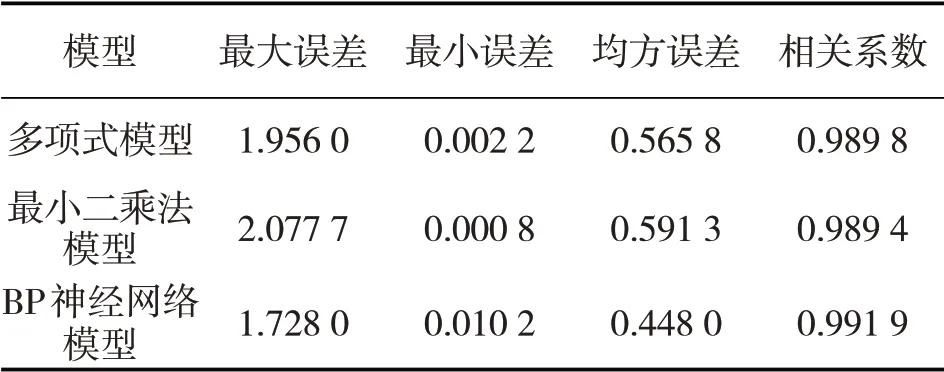
表1 3种模型评价参数

4 结论

基于钻井岩屑质量计量数据，研究了3种岩屑质量计量预测模型，解决了岩屑称重装置发生失效或者采集数据丢失而造成岩屑质量计量不准确、不连续的问题，为井眼清洁评价提供了依据。

1）结合岩屑质量计量数据，建立了岩屑流量预测多项式、最小二乘法、BP神经网络3种模型。通过数据仿真发现，BP神经网络模型在最大误差、最小误差与均方误差等参数指标上优于其余两种模型。

2）基于BP神经网络的岩屑流量预测模型可以帮助现场评价井眼清洁情况，实现岩屑质量实时、不间断测量，降低卡钻等非生产时间。

3）下一步需要将数据采集频率提高，综合考虑因其他因素导致的岩屑质量数据丢失或无法采集的问题。