基于DRNet的常微分方程模型逼近和序列预测方法
2022-11-03杨亚莉钟卫军
李 阳,杨亚莉,钟卫军
(1. 空军工程大学基础部,西安,710051;2. 文昌航天发射场指挥控制中心,海南文昌,571300;3. 宇航动力学国家重点实验室,西安,710043)
基于系统内部机理,常微分方程能够对复杂系统进行准确描述,进而实现对系统状态变量的预测。但是对于内部机理复杂或暂不清楚的系统,直接建立可靠有效的常微分方程较为困难。
近年来,随着软件和硬件的发展进步,对系统状态变量进行观测的方法更加多样高效,可获取的观测数据的精度越来越高、数量越来越多。人们基于观测数据进行了诸多研究。如通过符号回归对系统进行数值建模[1-2]、无方程建模[3]、非线性回归[4]、数据驱动人工神经网络(artificial neutral network,ANN)方法[5]。其中,文献[6~7]使用大量的观测数据驱动深度残差网络对自治系统进行了拟合逼近,实现了对系统状态的预测,但是该方法还存在模型预测精度不够高的问题。
Zhang等[8]在深度卷积神经网络的基础上引入残差机制和密集连接机制,提出的残差密集网络实现了图像的超分辨率重建。两种机制的引入使得该网络对数据特征的提取和利用更加充分,同时具有参数规模相对较小、便于收敛、避免“退化”等优点,在图像恢复[9]、视频超分辨率重建[10]等领域同样取得了良好效果。受此启发,在不增加观测数据规模的条件下,为进一步提高前馈神经网络(feed-forward neural network,FNN)对自治系统相轨线的拟合逼近效果,本文引入密集连接机制和残差机制,提出使用DRNet的方法对自治系统进行拟合逼近,实现对状态变量更高精度的预测。首先,利用系统的观测数据与相轨线的关系,将对自治系统的拟合逼近和序列预测问题转化为使用FNN对系统相轨线的拟合逼近问题。其次,为强化深层FNN对数据内含“特征信息”的提取和利用,提高对系统的拟合逼近效果,同时避免深层网络的“退化”(degradation)现象,提出并建立DRNet网络。而后,选择线性的单自由度系统振动模型[11]和非线性的SEIRS模型[12]、Logistic-Volterra模型[13]为示例,通过模型生成的观测数据训练DRNet,实现对系统模型的逼近和变量的预测。最后,将DRNet对示例模型的预测精度与残差网络(ResNet)、BPNN和密集网络(DenseNet)进行比较,验证本文DRNet方法的有效性,同时将DRNet应用于含噪声数据集以验证其抗噪声干扰性。
1 模型建立
本节将对自治系统S的模型拟合逼近和序列预测问题转化为使用FNN对系统S的相轨线进行拟合逼近的问题。
假设自治系统S的状态变量X(t)满足方程:
(1)
式中:p=(p1,p2,…pr)T,r∈N+为常微分方程的参数,X(t)=(x1(t),x2(t),…,xq(t))T,q∈N+。如图1所示,系统S状态变量X(t)的相空间为D,将方程(1)积分得到系统S在D内的相轨线[14]
(2)
式中:Xl(0),l∈N+为系统S的初始状态。图1中曲线为系统S以X(0)为初始状态的相轨线。

图1 系统S的状态变量在相空间D内相图的示意图
假设系统S有便于观测的区域,记为D′。对于机理复杂或暂不清楚的系统S,方程式(2)未知。基于D′内观测数据对系统S的相轨线进行拟合逼近后即可实现对其状态变量的预测。
在D′内,对状态变量X(t)进行n次独立观测得到:
X(I)={Xj(tj)|j=1,2,…,n}
(3)
由式(2)知,{Xj(tj)|j=1,2,…,n}位于D′内的m(m≤n)条相轨线上。分别以X(I)中的n个观测值为初始状态,间隔Δt后再次对状态变量X(t)进行观测可以得到集合:
X(II)={Xj(tj+Δt)|j=1,2,…,n}
(4)
由集合X(I)和X(II)内状态值的对应关系,可得数据对集合:
Data={(Xj(tj),Xj(tj+Δt))|j=1,2,…,n}
(5)
在自治系统S内,Xj(tj)与Xj(tj+Δt)位于相同的相轨线[14],即(Xj(tj),Xj(tj+Δt))=(Xj(0),Xj(Δt)),
所以,式(5)中数据对集合可改写为:
Data={(Xj(0),Xj(Δt))|j=1,2,…,n}
(6)
并且由式(2)得:
Xj(Δt)=Fp(Xj(0),Δt),j=1,2,…n
(7)
因此,对自治系统S的研究及状态变量的预测问题可以转化为基于式(6)的观测数据对式(7)中映射Fp(·,·)——即系统S相轨线的拟合逼近问题。
根据人工神经网络的万能近似定理[15],FNN具有近似任意函数的能力。Wu等[16]的研究表明,当数据对规模相同时,分布于多条相轨线上的短间隔数据对比分布于少量相轨线上的数据对更能促进FNN对系统模型的逼近。因此在构造(6)式的数据集训练FNN对系统S的相轨线进行拟合逼近时,优先选择Xj(0)均匀分布于D′内的观测数据,并且观测的时间间隔Δt不宜太大。

式中:‖X‖2表示X的2范数的平方。选择合适的FNN,使用式(6)的数据集训练FNN使得损失函数L最小化,即实现FNN对系统S的相轨线的拟合逼近。此时,对系统S的相轨线的拟合逼近的问题转化为最优化问题:
式中:(Xj(0),Xj(Δt))∈Data。
2 DRNet方法
本节提出并详述DRNet方法,同时建立对照网络模型,确定模型的定量评价指标。
2.1 DRNet网络
深度神经网络含有更多的隐藏层,对函数的逼近效果更好[17]。Huang等[18]在深层卷积神经网络中提出的密集连接机制强化了隐藏层之间特征信息的传输和利用,同时减少网络参数并提高效率,在图像分类识别具有广泛应用。但是过多的隐藏层会使神经网络出现“退化”现象,即随着网络深度的增加,模型的准确率增加到一定程度后开始下降[19]。He等[20]提出的ResNet极大地消除了深层神经网络的退化现象,被广泛应用于图像处理的深度学习模型。为进一步提高对自治系统的拟合逼近效果并实现对状态变量更高精度预测,受残差机制和密集连接机制启发,本文在具有误差反向传播的FNN的基础上提出密集残差网络DRNet的方法。
一个N层的密集残差网络DRNet:Rn→Rm,其网络结构如图2(a)所示,其中“C”表示数据的拼接(具体如图2(b)所示),“+”表示数据的相加。在DRNet中,第i-1层的任意一个神经元均和第i层的所有神经元相连(i表示隐藏层内任意一层的序号)。
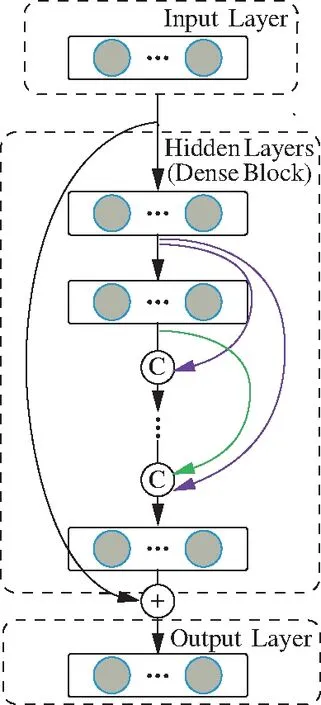
(a)DRNet
在DRNet的隐藏层内,将前i-1层的输出拼接后作为第i层的输入,形成密集连接模块。此时,每层均能直接接收前面各层提取的特征信息,使得浅层特征和深层特征都得到更加充分的利用,加强了各隐藏层之间特征信息的流通,能够提升各层特征信息的利用率,在一定程度上减少了网络模型的参数数量[21],同时,有效地缓解了梯度消失的问题。因此DRNet的第i层输入为:
Xinput,i=[Xoutput,1,Xoutput,2,…,Xoutput,i-1]T
(8)
式中:[X1,X2,…,Xn]表示数据X1,X2,…,Xn的拼接。第i层输出为
Xoutput,i=Hi(Xinput,i)=
(9)
式中:σi为该层激活函数,文中均选择为tanh;Wi和bi为该层需要通过训练确定的参数。
为进一步消除深层DRNet可能出现的“退化”问题,引入残差机制,将DRNet的输入层与输出层直接相连,即第N-1层的输出与DRNet的输入相加作为DRNet的输出:
Xoutput=Xoutput,N-1+Xinput
(10)
综合考虑系统观测数据的规模、计算消耗、网络收敛性能和误差精度的平衡,本文示例中的DRNet网络除输入层和输出层由状态变量X的维度决定外,隐藏层数h和每层神经元数目m分别在{3,4,5,6}和{20,30,40,50}中选择。根据DRNet在数据集上最小损失函数来确定最优模型的隐藏层数和各层神经元数目。此外,DRNet的优化器选择为Adam算法、损失函数选择为均方误差函数(Mean Squared Error Loss,MSELoss)、学习率设为0.01、batch_size设置为10。
如图1中曲线所示,DRNet经过观测数据的训练,实现对方程式(2)的拟合逼近后,即可对系统S的状态变量进行预测:
(11)
2.2 对照网络模型
为评价DRNet方法的有效性,本文选择BPNN、ResNet[7]和DenseNet[8]作为对照网络模型。由网络结构可知,DRNet比BPNN多了密集连接机制和残差机制,比ResNet多了密集连接机制,比DenseNet多了残差机制。对照模型的隐藏层数h、每层神经元数目m的确定方式、优化器选择和损失函数选择同DRNet一致。
2.3 评价指标
为定量评价DRNet方法的性能,对于预测值,本文选取的评价指标为均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、拟合优度(R-squared,R2)。其中,MSE、MAE和MAPE反映出预测值与真实值之间的偏差,其越接近0,表明预测值越接近真实值。R2反映出预测值与真实值的相似程度,其越接近1,表示拟合程度越高,预测效果越好,DRNet对系统模型的拟合逼近越完美。
3 应用结果及分析
为验证DRNet方法在常微分方程模型中应用的有效性,将其分别应用于线性的单自由度系统振动模型和非线性的SEIRS传染病模型、Logistic-Volterra模型。首先,通过式(3)、式(4)获得X(I)和X(II)。不失一般性,假设X(I)在示例模型的便于观测相空间D′内服从均匀分布。X(II)通过LSODE算子[22]基于示例模型方程和X(I)得到。而后,由式(5)、式(6)构造训练DRNet和对照网络模型所需的数据集
Data={(Xinput,j,Xoutput,j)|j=1,2,…,n}=
{(Xj,Xj(Δt))|j=1,2,…,n}
为更加科学地验证DRNet的性能,在每个示例模型中,分别构造规模为5 000和10 000的数据集,记为Data-5k、Data-10k。此外,为评估DRNet的抗噪声性能,在数据集Data-5k上加入5%的噪声,得到噪声数据集,记为Data-5kN。
3.1 单自由度系统振动模型
根据受力分析和牛顿第二定律,无驱动有阻尼单自由度弹簧的振动系统的微分方程为:
(13)
对于某一单自由度振动系统,根据模型参数含义,实验中选择D′=[-3,0]2,并随机取定参数(a,b)=(0.2,2)。当Δt=0.1时,生成数据集,驱动DRNet和对照网络模型完成对系统(13)的拟合逼近。根据多次试验的损失函数,在Data-10k上表现最优的DRNet含有4个隐藏层、每层30个神经元,在Data-5k上表现最优的DRNet含有3个隐藏层、每层40个神经元。对于D′内任意初始状态X0=(-1,-3),训练完毕的最优DRNet在t∈[0,20]内的预测结果见图3。从图中可见,DRNet在Data-5k,Data-10k和Data-5kN上均实现了对单自由度系统振动模型的拟合逼近。
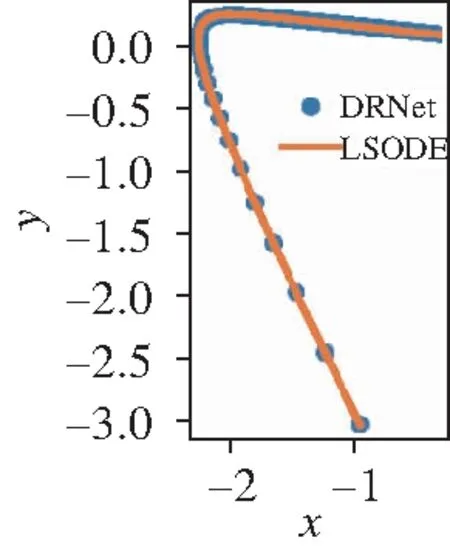
(a)Date-10k
DRNet和对照网络模型的评价指标见图4,从上往下依次为Data-10k、Data-5k和Data-5kN(以下各图类同)。由图可见,在Data-5k和Data-10k上,DRNet的表现均优于对照网络模型。DRNet在噪声数据集Data-5kN上性能稍有下降,除平均绝对百分比误差(MAPE)劣于ResNet外(1.6%>0.85%),其他3项指标均表现优异。

(a)MSE
3.2 SEIRS模型
利用数学方程(组)模型来描述和分析传染病的传播规律是常微分方程的重要应用方向之一。根据不同传染病的免疫特性,人们陆续建立了不同的仓室模型。如脑膜炎、淋病等,患者康复后不具有免疫力,可以再次被感染。据此可以建立SEIRS模型,其微分方程为:
(14)
式中:S、E、I、R分别表示易感者、潜伏者、患病者、康复者在人群中的占比,因此可知(S,E,I,R)∈[0,1]4。
针对某一地区的某一疾病,根据参数的生物学含义和经验,实验中选取D′=[0,0.5]4,并随机选择参数(β,σ,γ,μ)=(0.8,0.3,0.4,0.3)。当Δt=0.2时,生成并构造数据集,驱动DRNet和对照网络模型对系统(14)拟合逼近。根据多次试验的损失函数,在Data-10k上表现最优的DRNet含有6个隐藏层、每层50个神经元,在Data-5k上表现最优的DRNet含有5个隐藏层、每层20个神经元。对于D′内任意的初始状态(S,E,I,R)t=0=(0.5,0.5,0,0),训练完毕的最优DRNet在t≤20的预测结果如图5中圆点所示。由图5中结果可见,DRNet在3个数据集上均较好地实现了对SEIRS模型的拟合逼近。

(a)Date-10k
DRNet和对照网络模型的评价指标见图6。从图中的4个定量评价指标可知,在3个数据集上,DRNet的表现均优于对照网络模型。

(a)MSE
3.3 Logistic-Volterra模型
20世纪20年代,致力于微分方程应用研究的意大利数学家Volterra在研究捕食与被捕食关系时提出了著名的Volterra模型。在该模型中考虑系统内捕食者与被捕食者自身的阻滞作用时,为Volterra模型加上Logistic项,得到Logistic-Volterra模型,其微分方程组为:
(15)
选取某Logistic-Volterra系统,根据生物学经验随机取定(r,s,a,b,m,n)=(1.1,0.4,0.2,0.03,90,30),D′=[0,30]×[0,6]。当Δt=0.5时,生成并构造数据集,驱动DRNet和对照网络模型对系统(15)拟合逼近。根据多次试验的损失函数,在Data-10k上表现最优的DRNet含有3个隐藏层、每层20个神经元,在Data-5k上表现最优的DRNet含有3个隐藏层、每层50个神经元。对于D′内任意初始状态X0=(25,2),训练完毕的最优DRNet在t≤50的预测结果如图8所示。图可见,DRNet在3个数据集上均较好地实现了对Logistic-Volterra模型的拟合逼近。

(a)Date-10k
DRNet和对照网络模型的评价指标见图8。从图中4个定量评价指标可知,在3个数据集上,DRNet的预测精度优于对照网络模型。

(a)MSE
3.4 结果讨论和参数分析
从图3、图5、图7可见,经过数据集Data-5k和Data-10k训练后,DRNet对系统状态变量的预测值与LSODE算子得到的参考值较为契合,表明DRNet方法较好地实现了对模型的拟合逼近,具有对状态变量进行准确预测的能力。由图4、图6、图8中的定量评价指标可见,DRNet在2个数据集上的预测精度均超越了ResNet,DenseNet和BPNN,并且相比于线性的常微分方程系统,DRNet在非线性常微分方程系统上的评价指标均比对照网络模型更好,不仅表明DRNet在不提高数据规模的条件下,实现了对系统模型的更高精度预测,更表现出DRNet方法对自治系统模型逼近和序列预测的高有效性。在抗噪声方面,经过Data-5kN训练的DRNet虽然性能有所下降,但是依然具有良好的预测精度,均方误差小于对照网络模型,这表明DRNet具有较好的抗噪声干扰性能。
在3个示例模型中,从数据集Data-5k到Data-10k,最优DRNet含有的隐藏层数h和每层神经元数量m变化不大;且在数据集Data-10k的预测精度要优于其在Data-5k的预测精度,这表明可以通过增加数据集规模的方法提升DRNet的预测精度。但是对于很多系统而言,获得大量观测数据的成本是巨大的,并且由图5、图7、图9中的定量评价指标可见,当模型精度已经很高时,大幅增加观测数据集规模对提高预测精度的效果较为有限。
4 结语
本文研究了密集残差网络DRNet对自治系统进行模型拟合逼近并实现状态变量预测的问题。在示例模型应用中,DRNet可实现媲美LSODE算子数值解的优异结果,预测精度优于ResNet、DenseNet和BPNN,并且在非线性系统上,DRNet的定量评价指标明显优于对照网络模型;在面对较小噪声的干扰时,DRNet的性能没有出现大幅下降,展现出了较好的抗噪声干扰能力。这为利用观测数据研究机理复杂或暂不清楚的系统提供了新的有效方法。
