小型航空Wankel发动机转子结构优化仿真

何光宇，杨正浩，耿 琪

(空军工程大学等离子体动力学重点实验室，西安，710038)

21世纪以来，军用无人飞行器技术持续发展，尤其是小型无人机组成的分布式集群作战在未来战场上将发挥着愈加重要的作用[1-2]，随之而来其对动力系统的需求也日渐突出。Wankel转子发动机凭借其功率高、结构简单、传动平稳、体积小、质量轻、造价低等特点[3-4]，在无人机动力领域有着独特的优势[5-6]。小型航空转子发动机工作时，存在温度低、气压低使得燃烧效率低，风冷的冷却方式使得冷却效率较低，体积小且功率高使得部件承受载荷较大等问题，再加上三角转子是转子发动机最主要的运动部件，其在工作时要承受工作室的燃气爆发压力、摩擦力，惯性力，同时还要承受工作室燃气燃烧产生的热负荷[7-8]，各种载荷相互耦合使得其工作环境复杂。而转子在这样恶劣工况下能否保证自身强度不发生破坏关系到发动机的整体性能，因此对于三角转子的结构设计显得复杂且尤为重要[9-10]。

目前国内对于转子发动机的研究，主要集中在性能计算方面，大多没有将发动机各部件的载荷以及强度因素考虑在内，少数对发动机部件的强度计算也只进行了静压力分析[9]，而没有考虑到转子实际复杂工况下受到的惯性力与热负荷，很难满足对转子在实际工况下受力分析的研究。

本文通过建立发动机工作热力学模型，获得发动机工作的缸温缸压曲线，以此作为边界条件，建立有限元模型计算转子工作时的温度场与应力场，并结合转子所受的机械边界条件，计算转子在热-力耦合下所受的应力与变形。在此基础上，分析转子所受的应力状态，并提出通过增大圆角和布置散热片的方法，以改善转子应力状态与应力分布，完成转子的优化设计。为转子发动机三角转子设计与结构优化提供方法和技术支撑。

1 边界条件与模型建立

1.1 三角转子有限元模型

以某小型航空用转子发动机为例，其采用单转子、风冷式航煤发动机，机型参数见表1。

表1 发动机主要参数

发动机的三角转子、缸体、端盖均采用球墨铸铁材料，有良好的耐磨与耐高温性能。其材料属性参见表2。为研究高温条件下的转子强度有限元分析，还需引入转子材料的性能参数随温度的变化关系，见图1。

表2 发动机材料性能主要参数

图1 材料物性参数-温度曲线

转子创成半径为60 mm、宽度40 mm，采用Multizone网格划分方法对转子进行高阶六面体网格划分，控制网格尺寸为2 mm，转子腰部、燃烧室凹坑等位置进行网格加密处理，结果如图2所示，有限元节点2 650 818个，单元1 825 406个。

图 2 转子网格模型

1.2 发动机零维模型

本文采取按时间积分的原则，基于Wankel发动机工作过程，建立发动机零维模型，模型以理想气体状态方程为基础，来考量工质温度、压力、体积与质量各状态参量之间的函数关系[11-12]，对于理想气体处于平衡状态时，满足：

pV=nRT

(1)

式中：p为气体压强；V为气体体积；n为单位体积内气体分子数；R为普适气体常数；T为气体温度。

本文根据Wankel发动机热力循环过程建立发动机的能量守恒、质量守恒方程[13-14]。如式(2)、式(3)所示：

(2)

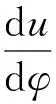
(3)

1.3 载荷及边界条件

作为本研究对象的三角转子，其所受的机械边界条件主要包括工作室内气体压力、旋转产生的惯性力、侧压力，由于其功率高、转速快，因此转子所受的惯性力较大，另外其侧压力对转子结构破坏作用影响较小，计算时进行忽略简化。

1.3.1 发动机零维模型

利用零维模型计算得到7 000 r/min转速下，缸内燃气压力的初始数据，单个循环周期内缸内瞬时压力变化如图3所示。并将其作为转子分析的机械边界条件。可以得到，在标定工况下0.018 1 s时，即曲轴转角为760°时，缸内燃气压力达到最高，约为1.5 MPa。

图3 瞬时压力随时间变化

1.3.2 转动惯性力载荷

转子的主要运动机构可以看做一个行星齿轮机构，转子绕偏心轴段中心Or转动，同时偏心轴绕中心线O做周转运动[15-16]，见图4。

图4 转子运动机构示意图

由平面运动学可知，转子运动的瞬时加速度中心C可以通过转子的角速度ωr与转子中心Or的加速度a0来确定。计算关系式如下：

(4)

(5)

最大燃气压力时刻下，曲轴转角为774°时转子工作位置达到图5所示。在求得转子瞬时运动状态与OrC后，得到转子的瞬时加速度中心，通过加载7 000 r/min转速求得惯性力。

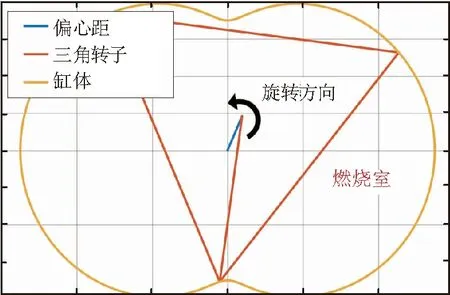
图5 偏心轴转角774°时刻转子与刚体相对位置示意

1.3.3 热边界条件

转子边界条件采用第三类简化边界条件，即给定燃气温度与换热系数。同样利用零维模型计算出单个工作室一个循环周期内，缸内工质温度、工质与转子工作面的换热系数随时间变化曲线，并以此作为转子的热边界条件，见图6。

图6 瞬时温度、换热系数随时间变化曲线

为简化计算成本，将传热过程看成一维问题，工作面一侧换热系数和换热流体的温度一定。结合工作室内温度与换热系数变化曲线，计算单循环内的平均传热系数αtm与平均温度Ttm[17]：

(6)

(7)

式中：αt为瞬时换热系数；Tt为燃烧室瞬时温度。采用串联热阻的方式求得转子其他各表面的传热系数[18-19]，并根据转子实际工况中温度值进行修正，转子各表面与各主要位置如图7所示，各表面温度与换热系数计算结果如表3所示。

图7 转子各表面与各主要位置示意图

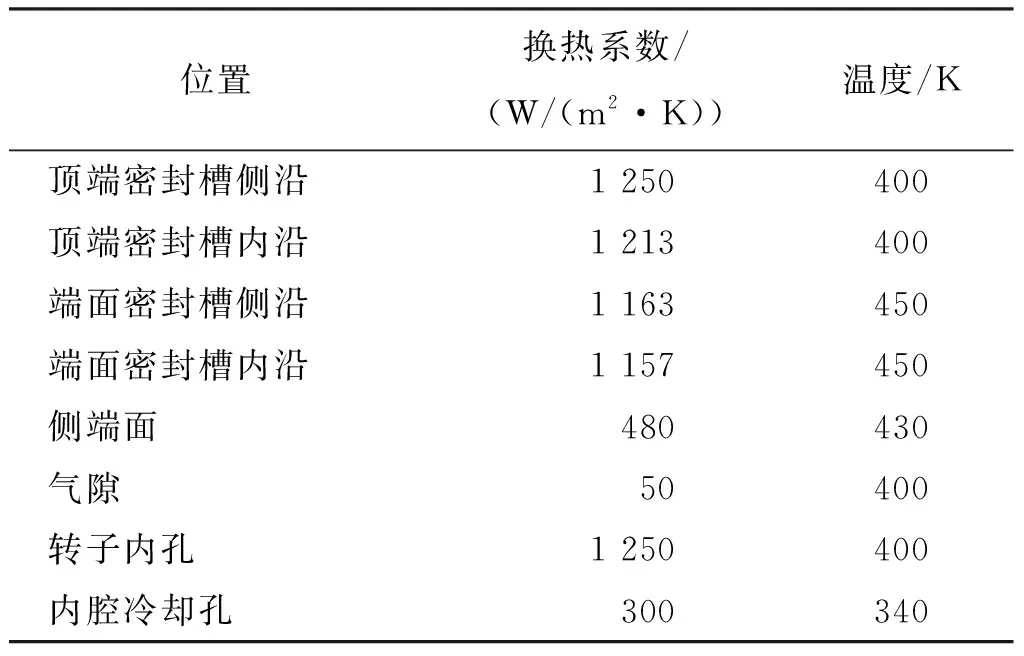
表3 转子其余各个表面温度与换热系数

2 热-机械负荷耦合分析

该型号小型航空转子发动机工作时，燃烧室瞬时温度最高可达1 200 K，燃气爆发压力约为1.52 MPa，取转子工况最复杂的最大燃气压力下的负载情况进行研究[9]，转子所受负荷以及有限元模型输入如图8所示。

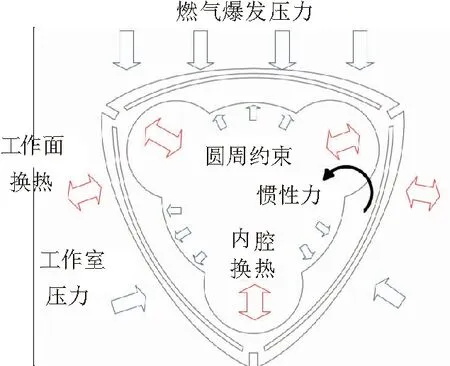
图8 转子所受负荷以及有限元模型输入示意图

2.1 机械负荷分析

假设工作室燃气压力以压强的形式均匀加载到转子工作面，惯性力通过计算转子加速度来加载，对转子中心轴承孔施加圆柱约束，限制其径向、周向与轴向位移，对转子端面施加法向约束。

静力计算时，转子所受到的侧向压力对转子结构影响不太明显，可近似为零[9]。本文选取转子工作最恶劣的工况，即转子处于最高燃烧压力下转子的静力学分析[20-21]。通过有限元分析，得到转子在最高燃气压力时刻下的应力与变形结果图9。由图9可知最大应力约为91.6 MPa，出现在转子腰部圆孔边缘。变形最大出现在转子承受燃气爆发压力一侧的顶端密封槽处，而不是燃烧室凹孔中央，约为0.19 mm，转子腰部处变形量较小，可以看出，相比较于燃气爆发压力，转子惯性力对转子所受的应力以及产生的变形影响更大。

(a)转子应力云图

表4为转子各位置编号以及应力值，可以看出，工作室凹坑中央与气隙中央由于承受燃气爆发压力，应力值较大，分别为19.0 MPa与25.6 MPa，腰部圆孔边缘处测量点应力值明显增大，约为62.1 MPa，此处出现明显的应力集中。

表4 最大燃气压力下各位置应力值

2.2 热负荷分析

计算所采用的换热边界条件见表2，转子受热不均会产生轴向与周向的热应力与热变形，若继续使用静力分析的约束条件，会使得计算结果应力过大，所以此处只对转子进行径向约束。

对转子进行温度场分析，得到此工况下转子温度场、热通量云图，结果如图10所示。由图可知，最高温度达到约552.9 K，处于燃烧室凹坑中心，最低温度约501.2 K，处于腰部圆孔面。

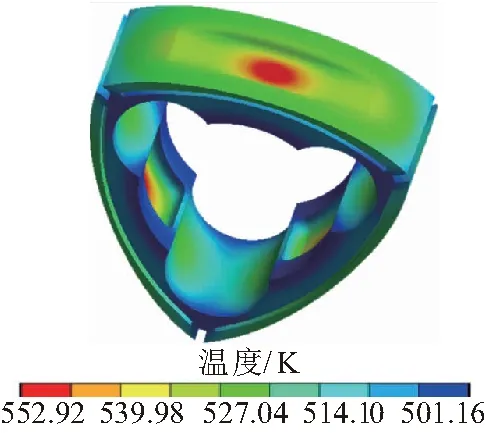
图10 稳定工况下转子温度场云图

转子所受热负荷以及变形见图11，可以看出，最大应力仍然出现在腰部圆孔边缘，约为636.3 MPa。转子顶端密封槽处出现较大的热变形，约为0.20 mm。可以看出温度场对转子应力应变影响比较均匀，应力、应变呈周向对称分布。

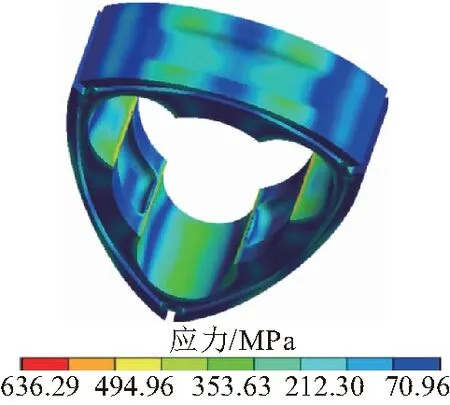
(a)转子热应力云图

表5所示为转子各位置的热应力值，可以得到，工作室凹坑中央与气隙中央应力值较大，分别为118.2 MPa与230.9 MPa，冷却孔、顶端密封槽等处由于温度梯度较大，其热应力值也较大，分别为186.7 MPa、262.9 MPa，腰部圆孔边缘处出现明显的应力集中，约为557.8 MPa，接近转材料的屈服极限值，安全余量不够充分。

表5 热负荷作用下各位置应力值

2.3 热-机械耦合分析

进行热-机械耦合有限元仿真时，仍保持其径向约束，在热仿真的基础上导入机械载荷，得到热机械耦合分析结果，其应力、应变云图为图12。可以看出腰部圆孔边缘应力集中现象最明显，最大应力约为687.0 MPa，最大变形量同样出现在距离转子加速度中心较远一侧的尖端密封槽处变，约为0.21 mm。转子各位置计算的应力值如表6。

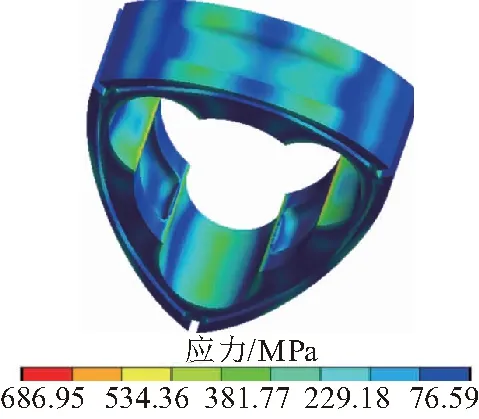
(a)转子应力云图

表6 热-机械耦合作用下各位置应力值

3 方案设计改进研究

3.1 增大圆角

针对转子腰部应力过大，出现应力集中的问题，我们对于转子腰部进行改进，腰部圆孔边缘加工圆角，以改善应力分布，解决腰部应力过大问题，如图13。重新计算得到最大燃烧工况下转子的应力、应变云图如图14。改进后转子应力场与未改进相比，最大应力由91.6 MPa下降到67.0 MPa，位置由腰部圆孔边缘改变为圆角处，最大变形量由0.19 mm变为0.16 mm。

(a)转子内腔圆角加工图

(a)改进转子应力云图

改进后最高燃烧工况下计算结果与原转子计算结果对比得到图15，各位置编号如表4所示，燃烧室凹坑与气隙应力值变化较小，平均下降2 MPa左右，改进后顶端密封槽压力由14.0 MPa上升至15.1 MPa，转子腰部圆孔边缘应力由62.1 MPa下降至31.0 MPa，应力值下降幅度较大，应力集中现象得到解决，改进后转子应力场得到改善。

图15 转子增大圆角改进前后各位置应力值对比

3.2 增加散热片

除圆孔边缘应力集中问题外，针对转子复杂的温度场问题，对转子冷却孔进行结构改进，在冷却孔内设置散热片，通过增大对流换热面积，来达到更好的冷却效果，如图16所示。

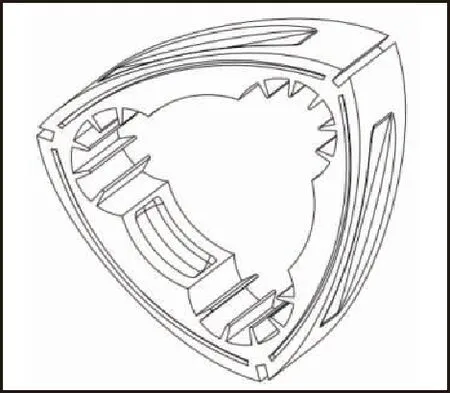
(a)转子散热片加工图

改进后的转子温度场如图17所示，改进前后主要位置温度场对比如图18所示，改进后转子最高温度仍出现在凹坑中央，并由原来的553 K下降到543 K，改进后转子最低温度出现在散热片上，冷却孔处温度由523 K降至487 K，距离冷却孔较近的顶端密封槽温度由515 K降至485 K。另外工作面、密封槽、腰部圆孔等处温度平均下降20 K以上。转子的工作温度更低温度场更加均匀，工况得到改善。

图17 改进转子的温度场云图

图18 转子增加散热片改进前后各位置应力值对比

布置散热片后转子的所受的应力、变形如图19所示，对比三角转子改进前后的应力、应变，得到图20，各位置编号如表5所示。可以看出，与改进前的转子相比，布置散热片的转子燃烧室凹坑、气隙与密封槽等处温度下降幅度较小，热应力下降幅度较小，平均下降25.0 MPa左右，而转子腰部圆孔边缘与冷却孔处温度均下降30 K以上，且温度场改善明显，热应力分别由原来的557.8 MPa、186.7 MPa，下降为521.2 MPa、120.9 MPa，分别下降36.6 MPa、65.9 MPa，相应的应力场改善效果也较为显著。同时，可以看出，最大应力仍然出现在腰部圆孔边缘，约为606.8 MPa，此处存在应力集中。改进后转子最大变形量位置不变，应变值由原来的0.20 mm下降为0.18 mm。

(a)改进转子应力云图

图20 转子增加散热片改进前后转子的热应力对比图

3.3 热-机械耦合分析

结合两种方案对转子进行重新建模，得到图21。

(a)转子改进图 (b)转子局部图

对模型进行有限元分析，得到热力云图以及热-机械耦合应力、变形量云图见图22。

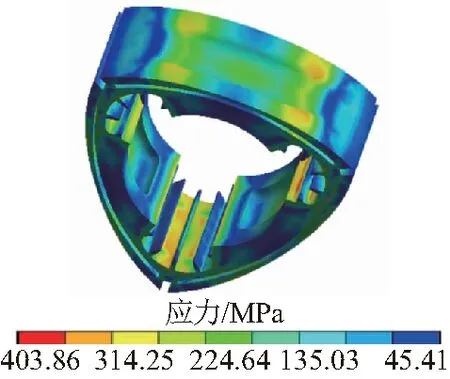
(a)改进转子应力云图

与原转子应力应变云图对比，得到图23。可以看出其应力集中处最大应力值大幅下降，由687.0 MPa降低到403.9 MPa，下降幅度约41.2%。应力集中现象得到缓解，最脆弱的转子腰部应力值由577.5 MPa降低到306.1 MPa，下降约47.0%，由于布置散热片，冷却孔处温度场得到改善，其应力值由212.6 MPa下降至113.2 MPa，下降约46.8%，其他各处应力值都有小幅度下降，转子应力场得到改善。另外可以看出，转子变形量有小幅度下降，最大变相量仍出现在距离瞬时加速度中心较远的转子尖端密封槽处，由0.21 mm降至0.15 mm。

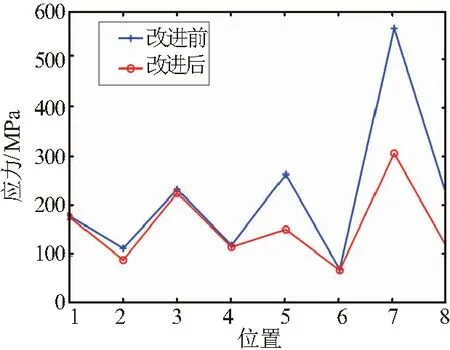
图23 改进前后转子热-机械耦合应力对比

4 结论

本文经过对小型航空Wankel转子发动机三角转子的有限元分析，提出了转子的结构优化方案，并对改进前后的温度场、应力、应变场进行对比，得到以下结论。

1)转子在工作中，工作面承受着燃气爆发压力，而腰部位置最薄弱，发动机设计时要着重注意转子腰部的结构设计。转子腰部圆孔边缘容易产生应力集中，通过增加圆角，可以将最大应力由原来的687.0 MPa下降为403.9 MPa，约为原来58.8%，腰部圆孔边缘应力由577.5 MPa下降为306.1MPa，降低为原来的53.02%，转子应力场得到改善。

2)通过布置散热片，可以增大散热面积，有效改善转子温度场，转子平均温度下降20 K以上，腰部边缘与冷却孔温度下降40 K左右，同时可转子工作面、气隙和密封槽等处热应力均下降30.0 MPa左右，冷却孔处应力由212.6 MPa下降为113.2 MPa，降为原来的53.3%。

3)结构改进对转子的变形量也有一定的改进作用，转子尖端工作时变形过大会导致尖端与缸体接触产生磨损，降低发动机气密性。进行热-机械耦合研究时，可以发现最大变形量往往出现在距离旋转加速度中心较远一侧的转子尖端密封槽上，改进后由原来的约为0.21 mm降至0.15 mm，符合工作要求，且一定程度提高转子与缸体之间气密性。