考虑误差不确定的航空制导弹药使用消耗预测方法
2022-11-03刘显光张晓丰苗青林高杨军秦丕胜
刘显光,张晓丰,苗青林,高杨军,秦丕胜
(空军工程大学装备管理与无人机工程学院,西安,710051)
随着世界武器装备的不断发展和各国军事战略的调整,航空制导弹药成为实现作战目标的重要武器。航空制导弹药相对于其他弹药而言具有造价高、数量少和保障要求高等特点,因此对于航空制导弹药实施精细化保障日益成为军方关注的焦点。航空制导弹药使用消耗预测是通过对过往航空制导弹药在日常战备值班中的使用寿命消耗数据进行分析,对未来航空制导弹药使用消耗趋势展开预测,从而为部队提前筹划航空制导弹药使用计划提供一定的数据支撑。
对航空制导弹药使用消耗进行预测通常可以采取参数输入预测和时间序列预测两种方式。其中,参数输入预测通过分析航空制导弹药使用消耗的影响因素,输入未来时间段内的影响因素参数来预测航空制导弹药的使用消耗。田德红等人将训练次数、训练天数、出动飞机架次、参与训练人数以及弹药储备量当作输入参数,分别构建了基于邻域粗糙集与支持向量机的航空弹药消耗预测模型[1]和基于变异粒子群优化与深度神经网络的航空弹药消耗预测模型[2]。愈杰等人利用反向传播网络(back propagation, BP)对弹药需求与打击目标和毁伤程度等相关因素之间的内在联系进行仿真分析,揭示了弹药需求与外部因素的非线性关系[3]。而时间序列预测主要是通过分析航空制导弹药使用消耗时间序列数据的特征分布,映射出消耗量在时间先后顺序上的相关性,并借此预测其未来的发展趋势。目前,常用的时间序列预测方法有自回归移动平滑法(auto-regressive moving average model, ARMA)[4]、灰色理论[5]和神经网络[6]等。周浩结合GM(1,1) 模型和灰色马尔可夫模型对航空器材消耗这类随机时间序列展开预测[7];周一鸣等人根据2007-2016年某型航空弹药保障装备器材消耗量的实际数据,建立了航空弹药保障装备器材消耗量的二次指数平滑模型[8]。
以上对航空弹药及保障器材的消耗预测均属于确定性预测,即通过给出一条确定的点预测曲线来刻画预测情况。而对航空制导弹药使用消耗开展预测,必须考虑到其实际条件:一是航空制导弹药造价高,必须充分利用每枚弹药的使用寿命,对预测的精度要求更高;二是航空制导弹药数量少,其使用消耗主要是指在日常战备值班中等级起飞以及地面检测中造成的使用寿命消耗,其数据量也相对较少;三是航空制导弹药的使用消耗受地区形势影响强,数据随机性高。因此,对于航空制导弹药的使用消耗预测考虑到其数据特点和预测要求,仅给出一条确定性的点预测曲线来准确反映航空制导弹药使用寿命消耗规律难以实现[9]。
置信区间估计是一种常用的不确定性处理手段,它用概率区间来描述预测值的不确定性,使用置信度来评估预测的可靠性[10]。通过置信区间估计能更好地涵盖航空制导弹药使用消耗预测过程中的不确定性,提升预测结果可信性。本文结合点预测误差数据对航空制导弹药的使用消耗进行置信区间估计,为航空制导弹药使用消耗提供了一种切实可行的预测方法。
1 基于SVR-PSO的航空制导弹药使用消耗点预测
由于支持向量回归(support vector regression, SVR)模型在非线性、小样本和随机性强的数据预测方面表现较好[11],故考虑采用SVR方法对航空制导弹药的使用消耗情况进行点预测。同时由于SVR模型的参数直接影响预测结果的好坏,利用粒子群优化(particle swarm optimization, PSO)算法对SVR模型参数进行寻优,提高模型的预测性能。
1.1 SVR算法原理
SVR常用来解决小样本、非线性回归问题,它在支持向量机(support vector machine, SVM)的基础上引入松弛变量的方式,按照结构风险最小化原则对数据进行精确拟合。
对于给定的航空制导弹药历史使用消耗数据{(x1,y1),(x2,y2),…,(xn,yn)};其中,xi表示第i个时间序列,yi表示第i个时间序列的航空制导弹药使用消耗情况,则SVR回归函数为:
y=w·φ(x)+b
(1)
式中:w为权重向量;φ(x)为某一固定的非线性映射;b为偏置量。
按照结构风险最小化原则,则SVR优化问题可以转化为最小化线性风险泛函问题:
yi-wTφ(xi)-b≤ε+ξ
yi-wTφ(xi)-b≤ε+ξ
(2)
式中:wTw表示样本的复杂程度;c为惩罚系数;ξ和ξ*为松弛因子;ε为不敏感损失系数。利用拉格朗日乘子法,上述问题可以演变为:
(3)
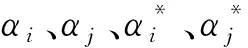
(4)
1.2 PSO算法寻优
在SVR预测问题中,需要引入惩罚系数c和核函数参数σ,这些参数的取值对预测结果有很大影响,必须选择合适的参数来对航空制导弹药的使用消耗进行预测。
PSO算法思想来源于对鸟类捕食行为的模仿。假设每个个体具有初始的位置x0和速度v0,算法通过跟踪每个个体与自身最优解p和群体最优解pg的位置关系来迭代寻优,粒子迭代过程如下:
(5)
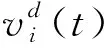
用PSO算法对SVR进行参数寻优,步骤如下。
Step1初始化粒子群,确定位置参数、粒子速度以及惩罚系数和核函数参数的取值范围,并设定惯性因子和最大迭代次数。
Step2计算每一个粒子适应度值。由于是对惩罚系数c和核函数参数σ寻优,所以适应度函数可以选取:
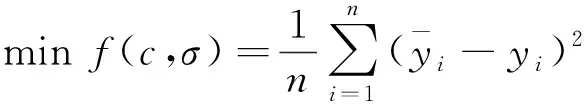
(6)
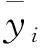
Step3更新自身最优解pi和群体最优解pg。利用式(5)和(6)更新粒子的位置、速度和适应度值,将每一个粒子更新后的适应度值与其经过的最好位置pi和所有粒子经过的最好位置pg进行比较,如果优于pi和pg,则用该粒子位置代替。
Step4判断是否达到终止条件。若达到,则输出全局最优解的位置即最优惩罚系数c和核函数参数σ;若未达到,则转至Step 3继续迭代。
2 基于KDE-HDRs的航空制导弹药使用消耗区间预测
由于SVR模型的预测精度和航空制导弹药使用过程中的各种不确定因素,预测结果和实际结果之间往往存在一定误差,而误差的累计会对后续航空制导弹药的使用决策造成影响。为了规避不确定因素(航空制导弹药在使用保障环节中的不确定性、日常战备起飞的消耗时间不确定性和预测模型不确定性等)和累计误差带来的影响,全面描述航空制导弹药使用消耗方面的不确定性,在点预测基础上利用误差不确定信息,采取置信区间估计预测,使未来实际使用消耗值落入某一置信度下的预测区间内,为后续弹药使用决策提供更充足的信息。
2.1 航空制导弹药使用消耗样本数据
航空制导弹药寿命通常包括日历寿命和使用寿命。日历寿命是指航空制导弹药的储存年限,随日历时间而均匀消耗;使用寿命通常包括通电时间和起落次数,主要是在航空制导弹药担负日常战备值班任务中由于等级起飞和地面检测产生相应消耗。
由于日常战备值班任务中等级起飞事件发生的不确定性,为了客观描述航空制导弹药的日常使用消耗情况,以季度为单位统计航空制导弹药使用寿命消耗数据,在数据整理过程中剔除轮战消耗、履历文件缺失和大规模地面检测等特殊情形。
以某区域某时间段航空制导弹药使用消耗的季度通电时间数据为参考(共收集整理出60个样本数据,其中选取前50个作为训练集,后10个作为测试集),对相关数据进行脱密处理后,构建航空制导弹药使用消耗数据样本。
2.2 航空制导弹药使用消耗预测误差分布
采用第1节中SVR模型和SVR-PSO模型分别对训练集进行预测,可以得到航空制导弹药使用消耗预测值与其真实值的预测误差情况,如图1所示。
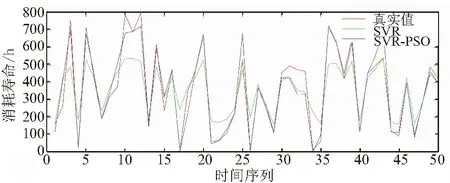
图1 航空制导弹药使用消耗点预测误差对比情况
从图1中可以看出,PSO算法寻优后的SVR模型对真实值拟合效果更好,更能准确反映航空制导弹药使用寿命消耗情况。
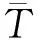
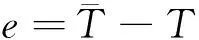
(7)
为了方便对误差进行统计分析,本文用相对误差来描述航空制导弹药使用消耗预测误差的统计特性,对误差进行归一化处理:
(8)
式中:e′为测试集中任意航空制导弹药使用消耗预测值与其真实值的相对误差;emin和emax分别为训练集中所有时间节点内航空制导弹药使用消耗预测误差中最小值与最大值。
使用SVR-PSO模型预测航空制导弹药使用消耗的误差分布及相对误差情况如图2所示。
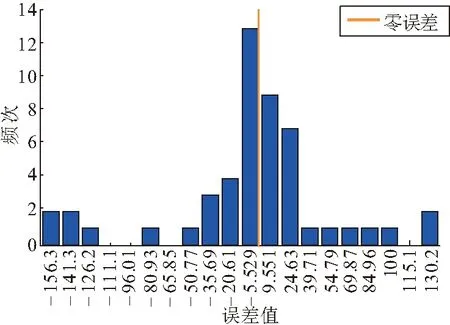
(a)误差分布直方图
从图2可知,在某些时间节点上,点预测误差波动较大,分析发现该类时间节点的误差波动是由于上级机关安排及地区形势变化所引起。该类样本点虽然会影响点预测模型的预测性能,但其可以进一步说明预测过程中的不确定性,为后续区间预测提供更多的不确定预测误差边界信息。
2.3 基于KDE的航空制导弹药使用消耗区间预测
一般来说,预测误差服从一定的数学分布规律,真实值往往在预测值周围分布。而要计算航空制导弹药使用消耗预测的误差概率分布,第一步往往是确定其误差概率密度曲线[12]。
求解概率密度曲线的方法可以分为参数估计和非参数估计[13]。其中,参数估计需先假定航空制导弹药使用消耗预测误差服从某一特定数学模型,再用已知样本估计参数,常用的数学模型包括正态分布、β分布和极值分布等。非参数估计不需要事先假定模型,而是直接根据已知样本信息估计航空制导弹药的使用消耗预测误差的概率密度,因而非参数方法比参数法更能反映样本的真实情况,常用的非参数估计有最近邻函数法、核密度估计法和样条函数法等。
分别使用参数估计法和非参数估计法对航空制导弹药使用消耗预测误差数据进行概率密度曲线拟合,误差拟合结果见图3。
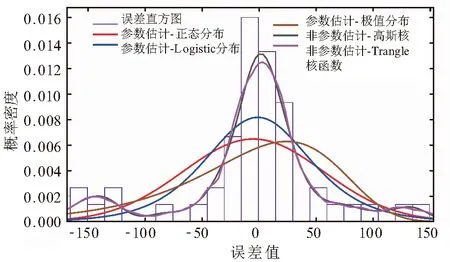
图3 不同估计方法概率密度估计曲线
由图3可知,由于航空制导弹药预测误差数据两端存在一定的波峰分布(点预测过程中预测误差波动较大的时间节点),与参数估计中事先假定的数学分布存在较大偏差,非参数估计法对上述航空制导弹药预测误差数据的拟合程度优于其他参数估计法,能更好的反映航空制导弹药使用消耗预测误差数据的概率密度分布情况。核密度估计法(kernel density estimation, KDE)是一种利用核函数基于有限数据元来评估总体数据分布的非参数估计法,其基于误差的核密度估计表达式为:
(9)
式中:h为带宽;N为样本数;ei为航空制导弹药使用预测误差样本;K(·)为指定核函数,主要有高斯核函数、三角核函数和Box核函数等。
对核密度估计法而言,性能的好坏主要是由选取的核函数类型和带宽取值决定的。当数据样本量足够大时,核函数类型选取对估计结果影响不大。而对于带宽取值而言,必须综合考虑拟合度和光滑性,带宽过大或过小都会影响最终结果的估计精度[14]。从期望积分平方误差(mean intergrated squared error, MISE)最小的角度可以求得最佳带宽h:
(10)
(11)
(12)
当核函数和样本数量确定之后,就可以得到最佳带宽h。
使用核密度估计法进行误差区间预测时,一般根据核密度概率函数,给定置信度1-η来求解置信区间。具体求解过程可参考文献[15],最终得到预测置信区间:
(13)
式中:el和eu分别表示置信度为1-η时的误差下限和上限:
(14)
式中:F-1(·)为累计概率分布函数的反函数,即对于F-1(λ)有P{x≤F-1(λ)}=λ。
2.4 基于HDRs的航空制导弹药使用消耗区间预测
对于核密度估计法而言,第2.3节中选择置信区间通常采用对称概率区间,即α1=η/2、α2=1-η/2。但实际上α1和α2的取值并不唯一,给定任一置信度对应着无数个置信区间选择。当预测概率密度曲线不是对称或单峰时,对称概率区间往往不是最合适的置信区间,尤其在现代许多时间序列预测模型中,时间序列呈现非线性或非正态分布,此时,预测概率密度通常也是非对称或多模态的。在这种情形下,使用最高密度域法(highest-density regions, HDRs)可以得到更为合适的预测区间[16]。
由2.3节中核密度估计法对航空制导弹药使用消耗预测误差进行估计,可以得到其概率密度曲线图4(核函数为高斯核函数,带宽h=4.579 1),可以看出其分布不是对称或单峰分布,此时适合采用HDRs来选择置信区间。
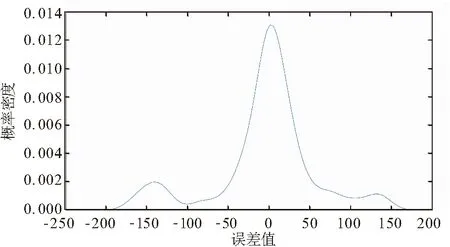
图4 航空制导弹药使用消耗预测概率密度曲线
最高密度域是指给定置信度下所占据密度最高的区域[17],通常满足:①在给定置信度的置信区间内,HDRs占据样本空间最小;②HDRs内点的函数值不小于该区域外点的函数值。由此可得在置信度为1-η时,其最高密度域选取置信区间为:
Rη={x:fX(x)≥fη}
(15)
式中:fη为满足P{X∈Rη}≥1-η的最大值。
由于HDRs占据样本空间最小,当给定置信度1-η时,只要计算出fη,就可以得出最高密度域的范围[17]。根据HDRs占据最小样本空间和密度最高的特点,利用HDRs选择置信区间可以为航空制导弹药使用消耗预测提供更为精确具体的预测区间。
3 实验分析
以第2.1节中航空制导弹药使用消耗数据为研究对象,采用MATLAB R2019a对数据进行实验分析。
3.1 预测效果评价指标
考虑不确定因素的航空制导弹药使用消耗预测最终是要为决策者提供未来一段时间内航空制导弹药的使用消耗可能情况,即航空制导弹药使用消耗预测的悲观值(置信区间上限)、理想值(点预测值)和乐观值(置信区间下限)。因此,对于预测效果的评价应分别考虑理想值预测(点预测)和区间预测结果的好坏,采用以下3个指标来对航空制导弹药使用消耗预测进行评价。
1)均方误差(mean squred error, MSE。式中简记EMSE)。表示预测值与真实值之间的差异程度,其值越小,表明点预测模型预测精度越高:
(16)
2)决定系数(R-Square)。 用来判断点预测模型对数据的拟合效果,其值越大,表明其拟合效果越好:
(17)
3)单位区间覆盖率(coverage per unit interval, CPUI)。表示给定置信度下置信区间对真实值的覆盖情况与区间宽度的比值,其值越大,说明区间预测模型的单位区间覆盖率越高:
(18)
3.2 航空制导弹药使用消耗点预测效果评价
为了验证SVR模型对航空制导弹药历史使用消耗数据的预测效果,将其与BP神经网络[18]和ARMA模型[17]进行对比实验。其中,BP神经网络和ARMA模型参数设置见表1。
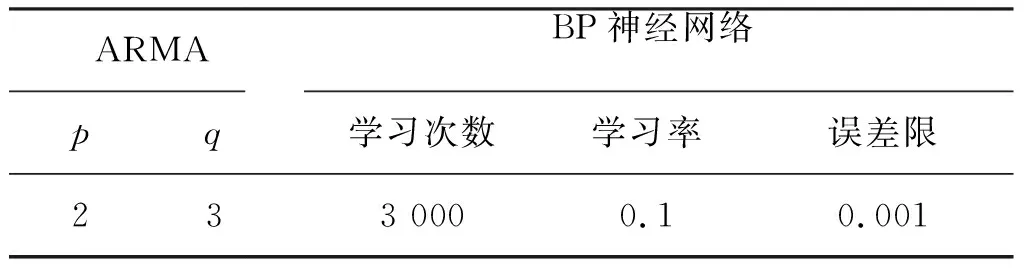
表1 模型参数设置
ARMA模型中p、q参数的确定是基于BIC(式中简记为CBIC)准则(Bayesian information criterion, BIC)确定:
CBIC=lnn-2lnm
(19)
式中:n为模型中参数的个数;m为模型的极大似然函数值。
利用这3类模型在测试集中对航空制导弹药使用消耗情况的预测结果来比较模型预测效果,预测结果如图5所示。
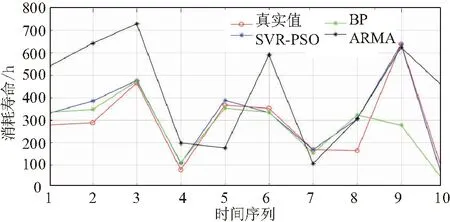
图5 测试集模型预测性能对比情况
从图5可以看出,BP神经网络和SVR-PSO拟合效果相较于ARMA模型预测效果较好,这说明对于非线性,小样本和随机性强的数据而言,ARMA表现欠缺,进一步比较预测性能指标MSE和R2的结果见表2。
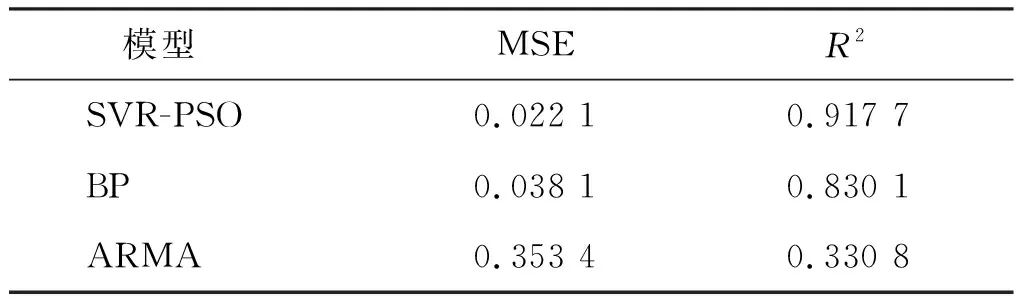
表2 点预测评价结果
从这两个性能指标数值来看,SVR-PSO模型对于航空制导弹药使用消耗数据而言,预测精度优于其他两种模型。因此,在SVR-PSO模型的基础上对航空制导弹药使用消耗开展不确定性预测可以得到更为合适的理想区间。
3.3 航空制导弹药使用消耗区间预测效果评价
按照2节中所述方法对航空制导弹药使用消耗进行区间预测。
给定置信度1-η=75%时,对SVR模型分别选取概率对称区间和最高密度域,将得到的置信区间同BP神经网络以及ARMA模型结合最高密度域得到的置信区间进行区间预测效果对比,预测结果如图6、表3所示。
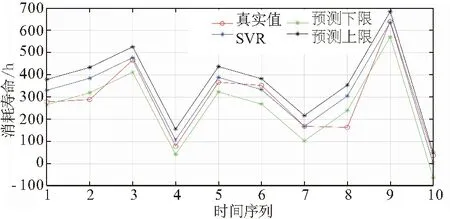
(a)SVR置信度75%对称概率预测区间
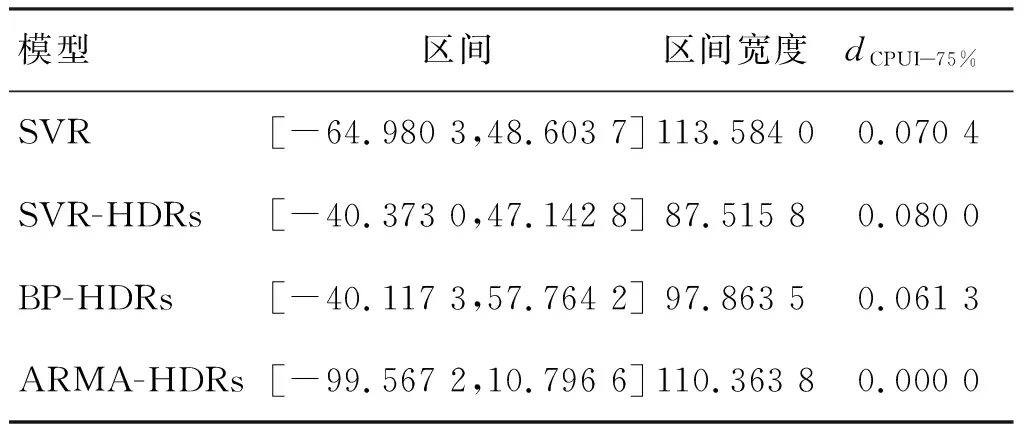
表3 区间预测评价结果
从图6和表3中可以看出通过最高密度域选取的置信区间与对称概率区间相比,在保证预测覆盖率的前提下尽可能减少了区间的宽度,从而缩小了航空制导弹药使用消耗区间预测的不确定性;同时,由单位区间覆盖率可以看出,SVR-HDRs在航空制导弹药使用消耗数据预测方面相较其他模型性能更好。
4 结论
近年来,由于缺少对航空制导弹药的使用寿命消耗预测研究,随着战备强度的不断提升,航空制导弹药使用消耗需求日益增大,航空制导弹药在使用安排上矛盾问题突出,造成航空制导弹药实际使用寿命浪费。本文结合航空制导弹药历史使用消耗数据特点开展预测,提供了一种科学合理的航空制导弹药使用消耗预测方法,为后续航空制导弹药使用安排提供了理论借鉴,主要结论如下:
1)SVR-PSO对于小样本、非线性和随机性强的航空制导弹药使用消耗数据而言,相较其他时间序列预测模型预测性能更好;
2)在点预测的基础上,从误差不确定性的角度出发,给出了能够反映未来航空制导弹药使用消耗的概率性预测区间,为后续制定弹药使用计划提供了理论参考;
3)依据HDRs理论对核密度估计中的区间选择进行优化。结果表明HDRs选择的置信区间,在指定置信度下可以得出更小的区间宽度并同时拥有相对更好的区间覆盖率。
本文给出了航空制导弹药使用消耗的点预测模型以及利用误差数据的区间预测模型,但在航空制导弹药使用消耗预测过程中,仅考虑误差不确定性不足以反映航空制导弹药使用消耗预测过程中的不确定性,后续应当考虑更多因素,优化预测模型,提供更为科学合理的预测结果。
