基于多元兰彻斯特方程的电火一体作战模型

毕 凯，李大喜，杨坤龙，曹永新

(1.93148部队，甘肃张掖，734100；2.空军工程大学防空反导学院，西安，710051)

近年来发生的一系列局部战争表明，电子对抗已成为不可或缺的作战力量，它改变了战争的形式和内容，并逐步成为重要的作战能力。一方面，战争形态已经由传统的“火力战”演变为“电子战+火力战”一体的作战样式，形成软硬兼施、全面压制的作战态势；另一方面，制电磁权已成为争夺战场主动权的关键高地，电磁频谱也已成为与陆海空天网并列的第六大作战域。现代战场中，电子对抗已成为“首战”利刃，是揭开战争的序幕，并贯穿战争始终。

随着电子对抗作用的日益突显，如何合理描述电火一体作战过程，准确分析电子战对火力的倍增器作用显得尤为重要。兰彻斯特方程[1]是1914年由英国工程师F•W•兰彻斯特提出，据古代冷兵器战争到近现代枪炮战争的不同特点，基于简化假设建立起一系列描述交战过程中双方兵力变化的微分方程组。兰彻斯特方程经过二战后数十年的不断改进和拓展，已广泛应用于作战仿真[2-6]、模型设计[7-8]、和运筹分析[9-10]等诸多领域。本文以现代多兵种协同作战为背景，在传统兰彻斯特模型基础上引入火力协同、电子防御、电子攻击等要素，构建了电火一体协同作战的兰彻斯特模型，并通过仿真，研究该模型对描述复杂电磁环境中的电火一体作战过程的合理性。

1 兰彻斯特方程

兰彻斯特方程中以第二线性律和平方律的过程描述更为符合现代战争形式，因此应用和研究最为广泛。

1.1 兰彻斯特第二线性律

兰彻斯特第二线性律方程通常用于描述远程打击武器在缺乏精确定位时的面压制场景。交战双方仅知道敌方兵力的大致部署位置，只能利用面火力压制，无法实现精确瞄准。因此，一方兵力的损失与敌、我双方兵力规模均正相关。设：①R(t)为t时刻红方兵力数量；②B(t)为t时刻蓝方兵力数量；③DR为红方单个兵力在单位时间内对蓝方部署区域内单个兵力的杀伤概率；④DB为蓝方单个兵力单位时间内对红方部署区域内单个兵力的杀伤概率。

则兰彻斯特第二线性律可表示为：

(1)

1.2 兰彻斯特平方律

兰彻斯特平方律模型用于描述精确瞄准条件下的交战过程。假设交战双方均在对方火力视野之内，在摧毁目标后可立即转火射击，则兰彻斯特平方律可表示为：

(2)

1.3 多元兰彻斯特方程

经典兰彻斯特方程描述简单，将战争中多兵种联合、多装备型号、复杂战场环境等因素用平均来表示，虽然具有一定合理性，但难以充分描述战场的复杂性。多元兰彻斯特方程可进一步描述多种兵力间的协同关系，构建更为细致的战争描述模型。

(3)

(4)

2 电火一体协同作战中的兰彻斯特模型

2.1 火力进攻与电子进攻

实际作战中，火力进攻任务相对明确，即以摧毁敌兵力实体为目标。但电子进攻内容相对繁杂，装备类型多，担负任务多，往往难以一概而论。一般可将电子进攻划分为电子攻击(EA)和电子防御(EP)两部分。

电子攻击，指为破坏或阻止敌方有效使用电子信息设备和系统而采取的主动攻击行动。现有电子攻击手段主要包括雷达干扰和通信干扰两大类，以致盲敌雷达、中断敌无线通信和瘫痪敌指控系统为作战目的。电子防御与电子攻击相对立，指在实施敌电子攻击条件下，为保护己方电子信息系统和设备正常发挥效能而采取的防御性手段，主要包括反电子侦察、反电子干扰和反电子摧毁等。

无论是电子进攻还是电子防御，其作战均以雷达、通信等电子信息设备的预防为中心，通过电子战手段，提升火力打击能力。

2.2 考虑信息效能的兰彻斯特方程

通过对比兰彻斯特第二线性律和平方律可以看到，第二线性律是在缺少敌情信息时的交战过程描述，而平方律则是在完全敌情信息时的交战过程描述。由于复杂电磁环境、干扰与反干扰的影响，实际作战往往是不完全信息对抗过程。

文献[1]给出一种体现信息效能的兰彻斯特模型：

(5)

式中：R(0)、B(0)为双方初始兵力，ε为信息因子，表示通过雷达、通信、指控等多手段敌对我方兵力位置的掌握情况，其值在[0,1]，当ε=0时，表示敌对我方兵力位置完全不掌握，此时式(5)与式(1)描述形式类似，此时交战过程类似于兰彻斯特第二线性律；当ε=1时，表示敌对我方兵力位置完全掌握，此时式(5)与式(2)形式类似，此时交战过程满足兰彻斯特平方律。

2.3 电火一体协同作战中的兰彻斯特方程

假设不考虑火力进攻和电子进攻作用距离的影响，即双方均在彼此的软硬杀伤范围之内；同一方、同型武器对敌方同型武器的作战性能相同。电火一体协同作战实质上可以看做电子进攻与火力进攻的联合作战，因此首先将式(5)做多元扩展：

(6)

进一步考虑对不同兵力的火力分配问题，引入分配权重ω,则式(6)可进一步表示为：

(7)

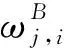
(8)

这里考虑一型火力进攻武器和一型电子进攻武器(兼具电子攻击和电子防御)协同作战的情况。令R1、B1分别表示配属双方的火力进攻兵力，R2、B2分别表示配属于双方的电子进攻兵力。

1)火力分配权重

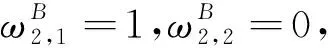
(9)

2)电火一体条件下的毁伤概率

武器的单体毁伤概率既与其单发命中概率p有关，也与武器装备的射速n相关。假设电子进攻不造成实体毁伤，考虑电火一体情况下己方电子防御对敌方射击精度的整体影响EdR(t)，则：

(10)

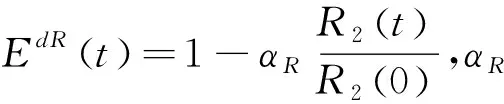
3)电火一体条件下的信息因子

信息因子反映的是目标掌握情况，影响信息因子的因素包括雷达侦察概率pRd、光学侦察概率pO、红外侦察概率pI等能力，以及指挥通信顺畅的概率pC，考虑电子攻击对情报获取和通信保障的整体影响，引入电子攻击效能系数EaR(t)，则：

(11)

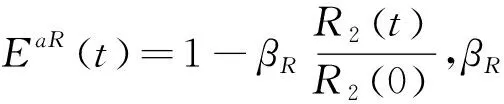
3 仿真与分析

假设在空地对抗中，红方为地面防空兵力，主要包括地面防空武器系统和电子进攻装备，蓝方为空中突袭兵力，主要包括对地突击飞机和侦察、干扰飞机，双方兵力及相关参数对比见表1～3。

表1 红蓝双方初始兵力对比

表2 红蓝双方火力进攻参数表

表3 红蓝双方电子进攻参数表

3.1 电火协同对作战过程的影响及分析

1)当双方均无电子进攻力量时(R2(0)=0，B2(0)=0)，作战过程如图1所示。T=40时，红方兵力消耗殆尽，此时蓝方剩余兵力80，由于受初始兵力的影响，蓝方以40的代价消灭红方100兵力。

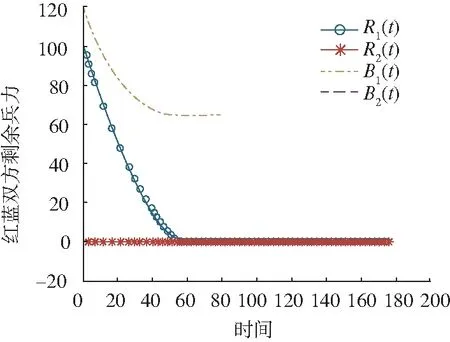
图1 无电子进攻理论时，红蓝双方作战过程

2)为双方加入电子进攻力量，(R2(0)=30，B2(0)=30)，作战过程如图2所示。T=132时，红方电子进攻兵力消耗殆尽；T=175时，红方火力进攻兵力消耗殆尽，此时蓝方剩余火力兵力27，剩余电子进攻兵力0。

分析图1可以看到，由于双方缺少电子进攻力量的支援，蓝方依靠火力兵力的优势迅速取得战场先机，作战进程推进迅速。在图2中，双方均加入电子进攻力量，由于电子防御、电子攻击对火力进攻效果的影响，作战过程呈放缓趋势。但是由于双方电子进攻力量相等，红方未能改变火力兵力劣势带来的不利影响，作战结果仍以失败告终。可见，在电子进攻力量相同的情况下，战争进程将被显著拉长。

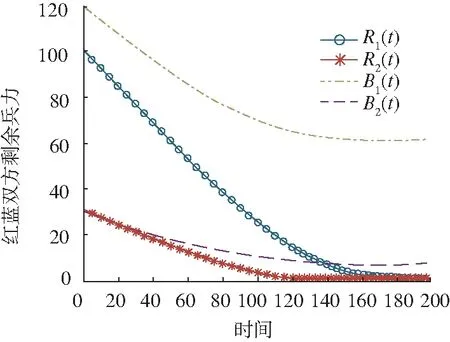
图2 红蓝双方电子进攻力量相同时作战过程

3.2 电子进攻兵力对作战过程的影响

进一步分析不同电子进攻兵力对作战进程的影响。令蓝方电子进攻兵力为10，红方电子进攻兵力分别为10、20、30、40，作战过程中双方兵力变化见图3～6。可得到以下结论。

1)随着电子进攻兵力的变化，战争胜负的天平逐渐由蓝方向红方倾斜。当红方电子进攻兵力由10增加至20，图4中蓝方电子进攻力量在T=10时消耗殆尽，此时红方依靠电子进攻力量的优势，使得火力进攻力量消耗速率明显降低。但在T=70时，由于红方电子进攻力量消耗殆尽，火力进攻力量消耗加快，最终未能取得胜利。在图5、图6中，由于红方电子进攻力量的继续增加，电子进攻力量优势进一步发挥，贯穿作战全程，最终使得红方取得战争的胜利。

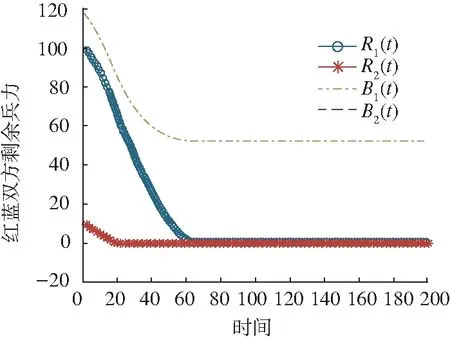
图3 红方电子进攻力量为10时作战过程

图4 红方电子进攻力量为20时作战过程

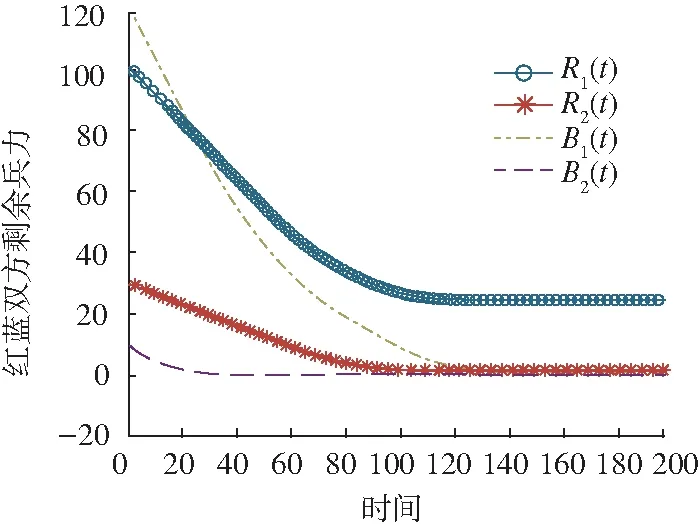
图5 红方电子进攻力量为30时作战过程

图6 红方电子进攻力量为40时作战过程

2)电子进攻力量是战争的倍增器，合理运用能够实现以小博大，以弱胜强。分析图3到图5的变化过程，在红方电子进攻兵力增加到26时，红方首次实现战争胜负的逆转，此时红方共出动火力进攻兵力100，电子进攻兵力26，共126，蓝方出动火力进攻兵力120，电子进攻兵力10，共130，既红方在总兵力处于弱势时，由于电子进攻力量的倍增，其取得最后胜利。

3)增强电子进攻力量，有利于保存自身实力，减少己方伤亡。在图5、图6作战过程中，当红方电子进攻兵力为30时，最终剩余火力进攻兵力22，电子进攻兵力5。当红方电子进攻兵力为40时，最终剩余火力进攻兵力41，电子进攻兵力19，可见随着电子进攻力量的增加，红方战场生存能力显著增强。

4 结语

本文在考虑电子进攻对作战过程影响的基础上，给出一种描述电火协同的多元兰彻斯特模型。该模型能够较为准确地描述作战过程中的火力分配、电子攻击、电子防御等因素的影响。通过仿真验证，模型推演结果与以往的战争经验接近，可见该模型具有一定的合理性。需要指出的是，现代战争的复杂性虽然远超文中仿真分析内容，但是如果能够给出火力分配、毁伤概率、信息因子等参数，利用式(8)总能给出接近的过程描述，因此本文模型具有较强的一般性描述能力。