基于轨道拟平根的合作目标机动跟踪UKF相对导航方法
2022-11-03杨盛庆陈筠力贾艳胜王嘉轶
杨盛庆 陈筠力 王 禹 贾艳胜 崔 佳 王嘉轶
1.上海航天控制技术研究所,上海 201109 2.上海市空间智能控制技术重点实验室,上海 201109 3.上海航天技术研究院,上海 201109
0 引言
高精度的导航数据处理是实现航天器智能自主控制的基础[1],航天器的高精度相对导航则是实现自主编队轨控任务的基础。不同的编队控制任务,譬如近程交会对接、编队保持、编队重构,其导航所需获取的状态信息也不尽相同。由于任务时间较短,交会对接的近程导引段与接近段一般采用CW制导。使用Hill方程进行相对导航,即能够获取较高精度的制导率所需的相对位置、速度信息。对地测绘领域,合成孔径雷达(synthetic aperture radar, SAR)载荷的干涉成像分布式卫星则需要实现长期的在轨自主编队保持和必要的编队重构。目前,在轨的分布式SAR卫星编队主要有PRISMA[2-3]、天绘二号[4]等。参考文献[5-6]提出了基于相对轨道拟平根的编队动力学模型。该模型通过定义编队构型参数,将Hill坐标系这类周期变化的相对状态参数转化为了仅具有长期项变化的相对轨道拟平根。由相对轨道拟平根构造的相对导航滤波算法能尽可能降低周期相对运动导致的导航误差,从而减小导航误差导致的控制代价。编队构型参数中轨道面内的沿迹向漂移和半长轴偏差,反映了双星在轨道面内的平均化的相对运动特征。但是,星间的半长轴偏差并非直接可测的物理量,其相关的观测方程具有较高的非线性,因此半长轴偏差的准确获取存在困难。参考文献[7]提出了一种基于约化相对轨道拟平根的卫星编队导航方法,基于沿迹向漂移的历史数据估计半长轴偏差,针对控制频率固定、控制间隔时间充分的多脉冲自主编队保持[8-10],能够实现长期稳定的高精度卫星编队相对导航。参考文献[7]所述方法,采用相对位置作为观测量,基于约化相对轨道拟平根构造了扩展卡尔曼滤波(extended Kalman filter, EKF)滤波算法。该方法所采用的EKF滤波算法相较无迹卡尔曼滤波算法(unscented Kalman filter, UKF),在处理非线性较强的动力学系统时存在不足[11]。当存在轨道机动时,EKF滤波算法中的状态估计和测量信息不符导致状态误差协方差矩阵的偏差累积,最终导致滤波发散,无法跟踪控制过程中构型参数的变化。参考文献[12]基于改进的编队Lawden方程构造UKF相对导航滤波,编队状态估计精度明显优于采用EKF的滤波方法。参考文献[13]构造了基于相对轨道拟平根的UKF滤波算法,该方法将雷达体制的测距测角信息转化为相对位置、速度信息,进而转化为相对轨道拟平根作为滤波算法的状态变量。参考文献[14]针对航天器气动辅助变轨问题,采用UKF进行参数优化估计。但是,上述方法均未考虑轨道机动对相对轨道动力学产生的影响。
未来,随着电推进的普及,自主编队保持的控制间隔将更短。高比冲的电推进,也为自主编队构型重构的应用提供了必要的基础,上述自主控制任务都对相对导航提出了更高的要求。但是,目前基于相对轨道拟平根的导航方法中没有考虑轨道机动跟踪的滤波算法。轨道机动的跟踪有多种方式,滤波器设计层面有渐消因子自适应滤波等方式[15]。但核心的问题还是建立更准确的动力学模型。参考文献[16]采用交互式多模型UKF算法,研究了地空导弹武器指控系统的机动目标跟踪方法。参考文献[17]采用自适应交互式多模型UKF算法,研究了小行星探测任务中小推力变轨过程的自主导航方法。考虑到合作目标的编队通常具有星间链路,能够有效测量双星之间的相对位置、速度和传递机动加速度信息。编队运动方程基于Hill坐标系,相对运动具有轨道周期特征。自然摄动下(主要是地球中心引力)的三轴相对加速度呈周期性,且数值大于机动控制产生的影响,基于Hill方程的滤波中机动加速度近乎于测量噪声,无法有效跟踪半长轴偏差变化。针对上述情况,充分利用可测信息,构造基于高斯摄动方程的相对轨道运动状态转移方程和高维状态观测方程能够有效跟踪轨道机动过程中构型参数的变化情况,有利于星上自主策略的快速生成和更新。
本文针对存在轨道机动的编队导航问题,提出了基于高斯摄动方程进行相对轨道拟平根状态估计的方法。同时,充分利用星间测量的相对位置、速度信息,建立高维观测方程,保证了导航滤波的实时稳定性,不再需要历史数据进行星间半长轴偏差的估计。本文方法能够有效跟踪轨道机动对编队相对运动产生的影响,给出连续稳定的相对导航结果。
1 相对轨道动力学与导航方法
1.1 Hill方程与相对导航
航天器编队在轨道系下的相对运动满足[5]

(1)
下标1,2为航天器编号,式(1)可以化简为
(2)
其中,
Hill坐标系与轨道坐标系转换为常值矩阵
式(2)两侧同乘Aoh可以得到Hill坐标系下的相对运动方程。式(2)两侧均为一次多项式,因此Hill方程在轨道系和Hill坐标系下的形式一致。
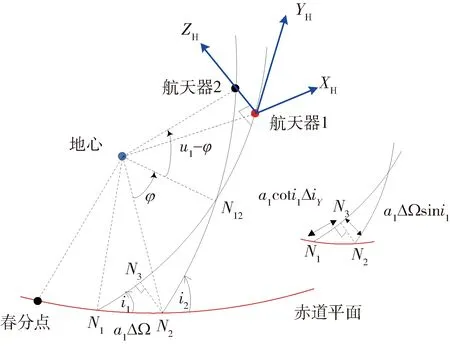
图1 卫星编队与Hill坐标系定义[7]
不同于交会对接近程段的线性逼近,椭圆编队的相对速度呈周期性变化,其相对加速度解析公式如式(2)所示。该项系统固有的相对加速度大于一般电推进系统实施轨道控制所产生的加速度。因此,基于Hill方程的相对导航中加入推力效应等效于系统状态转移时的噪声,无法体现对相对轨道特征的影响。
编队构型参数与Hill坐标的转换关系为
(3)
上述编队构型参数能够较好地反映相对运动的几何特征。沿迹向漂移l为相对运动的椭圆中心与主星的距离,星间的半长轴偏差Δa可以理解为沿迹向漂移的变化速率,是与沿迹向漂移相关的统计量。
使用Hill方程的相对导航能够较好地跟踪轨道机动情况下的相对位置、速度信息,及部分编队构型参数,但无法快速准确获取半长轴偏差。实时导航滤波过程中,式(3)中的Δa只能置零处理。构型参数无法跟踪真实的变化情况,不能满足自主轨道控制的控制策略输入要求。
1.2 基于相对轨道拟平根的相对导航
定义相对轨道拟平根[7]
(4)
式(4)中,ak,ek,ik,ωk,Ωk,uk(k=1,2)均取轨道平根。定义标量δe,δi满足

定义如下编队构型参数,相对轨道拟平根与编队构型参数的转换关系满足

参考文献[7]提出的基于约化相对轨道拟平根的卫星编队导航方法,克服了模型线性化造成的误差。该方法仅使用相对位置作为观测量,且需要使用较长时间积累的历史数据估计半长轴偏差。对于轨道机动情况,无法有效跟踪相对拟平根的变化情况。机动后需要重启导航,实现新状态的建立。
2 轨道机动跟踪滤波
2.1 高斯摄动方程与状态转移方程

(5)

(6)
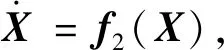
(7)
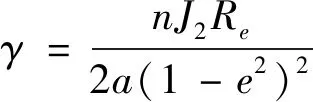

2.2 高维观测方程
为了克服观测方程的非线性对于Δa估计不准的问题,设计采用高维的观测方程。即充分利用合作目标能够获取的相对位置、速度和机动加速度等测量信息。
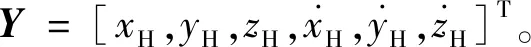
考虑轨道机动的相对轨道拟平根的观测方程取Y=h(X),分量满足式(8)。

(8)
2.3 无迹卡尔曼滤波
UKF采用无迹变换描述非线性方程函数泰勒级数展开的二阶项和其它高阶项,通过少量样本及其非线性变换后的均值和方差作为状态预测、测量预测和相应的方差阵[15]。UKF可以达到二阶滤波精度,而不必对非线性函数进行求导,适合本文构造的机动跟踪相对导航模型。从方法实现难宜程度和导航精度方面相较EKF都具有优势。
记系统状态转移方程和观测方程为
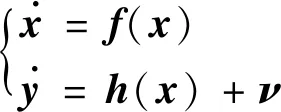
UKF的算法流程如下[18]。
(a) 初始化

其中,l为滤波器状态变量的维数,α,k为可设滤波器参数。
(b) 选择Sigma点
χi,k-1=
(c) 状态预测
χi,k |k-1=f(χi,k-1)
yi,k |k-1=h(χi,k |k-1)
(d) 量测更新
上述式中Qk和Rk分别为系统误差协方差矩阵和量测噪声协方差矩阵。需要指出,针对不同工况下的Qk和Rk优化是智能控制研究的一个重要方向。

图2 机动跟踪的UKF导航滤波流程图
3 导航算法的仿真验证
3.1 基于Hill方程的相对导航
为了充分验证导航算法对各向轨道机动的跟踪能力,仿真设计了轨道系下径向、切向、法向这三个方向的4次机动。考虑卫星质量1500kg,配置40mN电推进,推力加速度为2.67×10-5m/s2。轨道机动的实施情况如图3所示,相较自然摄动下相对周期运动对应的相对加速度,轨道机动的加速度相对较小。
相对测量考虑差分GNSS体制的测量精度,相对位置测量单轴精度0.1m,相对速度测量单轴精度0.001m/s。加速度测量ak考虑10%的偏差,采用如下式的简易滤波anav(tk)=0.2·ak+0.8·ak-1。
根据仿真结果可以观察到,基于Hill方程的相对导航,能够跟踪Hill坐标系下的相对位置、速度变化,如图4所示。但是,对于构型参数中半长轴偏差Δa无法有效跟踪。如图5所示,动力学曲线能够有效反应历次轨道机动的变化过程,体现为构型参数的变化。但是,基于Hill方程的UKF滤波无法精准确定星间的半长轴偏差。导致采用式(3)计算编队构型参数时相关参数的失真现象,无法连续并准确地确定机动过程中的编队构型参数。

图3 自然摄动和轨道机动在轨道系下各轴变化情况

图4 基于Hill方程的相对导航的相对位置、速度确定精度
3.2 基于轨道拟平根数的相对导航
使用本文所述的UKF相对导航方法,进行轨道系下三个方向轨道机动的跟踪。UKF滤波器参数取值α=0.001,k=0。
滤波仿真结果如图6和8所示,作为比对实验,设置了未采用机动跟踪状态转移方程的导航滤波仿真,结果如图7和9所示。仿真结果表明,本方法能够有效跟踪机动过程中构型参数的变化,半长轴偏差的确定维持了较高的精度。

图5 基于Hill方程的相对导航构型参数
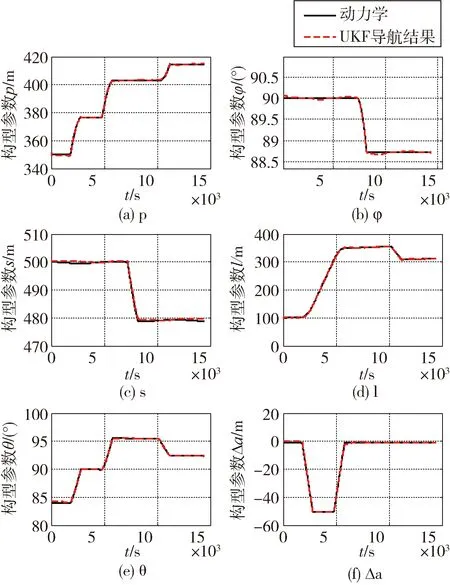
图6 基于本文方法的相对导航结果

图7 未采用机动跟踪状态转移方程的相对导航结果

图8 基于本文方法的相对导航精度
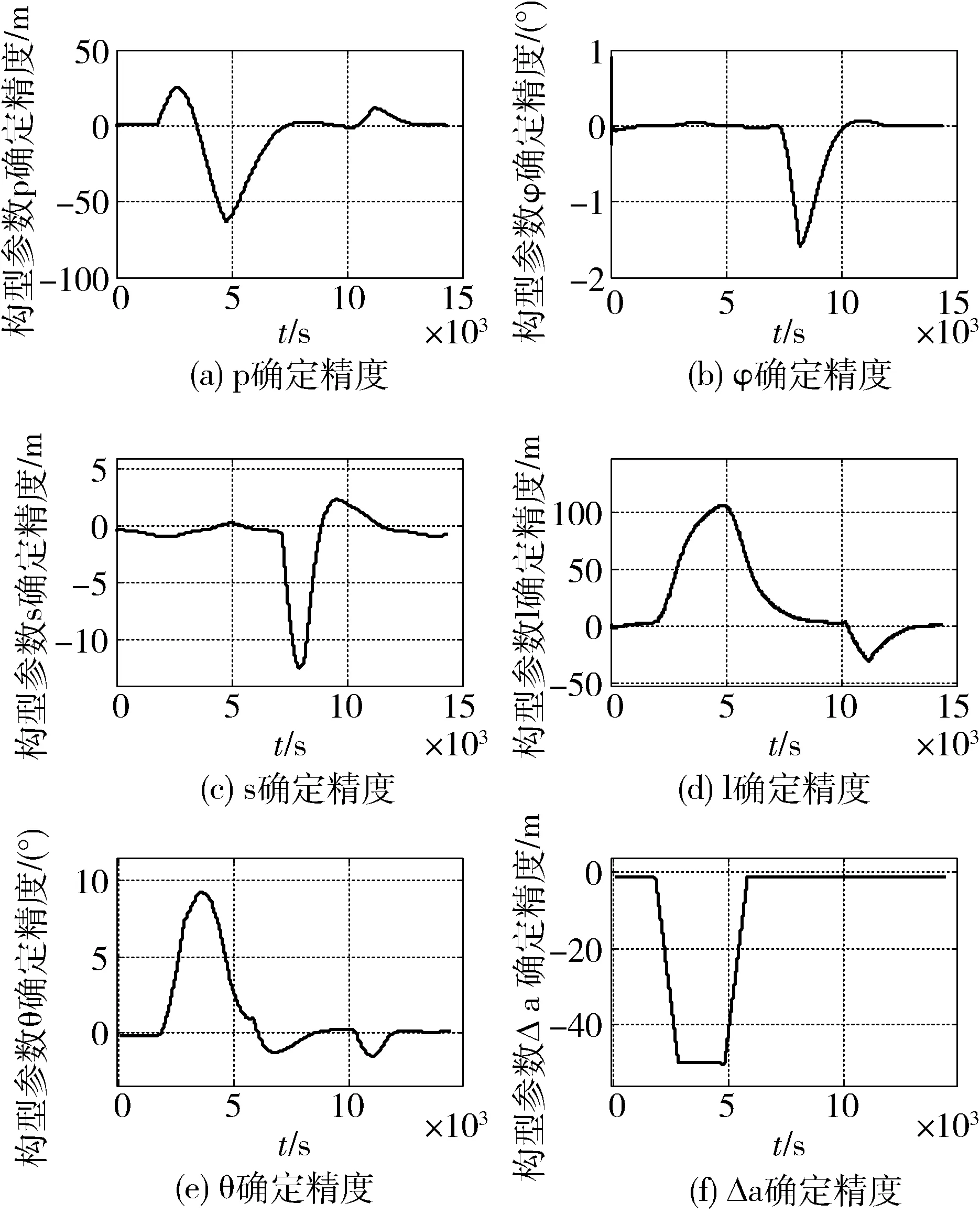
图9 未采用机动跟踪状态转移方程的相对导航精度
4 结论
提出了一种基于轨道拟平根数的UKF相对导航方法。针对基于Hill方程或者约化相对轨道拟平根的相对导航所存在的不足之处,考虑将高斯摄动方程引入到相对轨道拟平根的状态转移方程。推导了高维的观测方程,结合UKF滤波算法,实现了针对编队构型参数和星间半长轴偏差的高精度相对导航。
本文方法充分利用合作目标相对位置、速度和机动加速度等测量信息,能够跟踪轨道机动对相对运动产生的影响,连续给出控制策略所需的相对导航结果。
