一种考虑非线性形变的柔性航天器边界稳定控制方法

2022-11-03魏春岭

航天控制 2022年5期

袁泉魏春岭张军

1. 北京控制工程研究所，北京 100094 2. 空间智能控制技术重点实验室，北京 100094

0 引言

空间太阳能电站作为大型空间结构，在结构尺寸上达到公里量级，呈全柔性状态，即不存在刚性构架。与刚体结构相比，全柔性航天器的空间分布特性使得相应的动力学模型描述与控制问题变得更加困难。Wie等[1]针对位于地球同步轨道的太阳能电站卫星，设计了采用电推力器的轨道姿态控制系统，通过低控制带宽降低结构振动与控制的相互作用。Wu等[2]将太阳能电站卫星视作刚体，考虑重力梯度、太阳光压等摄动作用，利用抗扰技术与LQR理论设计了鲁棒最优太阳指向控制策略。Ji等[3]基于多刚体动力学模型设计了空间太阳能电站卫星姿态控制系统。Fujii等[4]通过数值与实验的方法研究了绳系空间太阳能电站卫星的振动控制问题。Li等[5]考虑了轨道姿态振动耦合的太阳能电站卫星动力学控制。

边界控制由于实现形式简单，在分布参数系统的控制中得到了大量的研究与应用。Lagnese[6]研究了部分边界固定、部分边界自由的线性弹性动力学系统的边界稳定问题，给出使得系统一致稳定或强稳定的边界控制。Lasiecka[7]考虑了二阶Petrovsky型演化方程的非线性边界稳定问题。Balakrishnan[8]分析了一端固定、一端自由且受控制力与力矩作用的Bernoulli梁的等比例阻尼问题。Leugering[9]利用速度反馈，给出了含Boltzmann型弱黏弹性阻尼的悬臂梁的一致稳定边界剪切力控制。Ma等[10]分析了一端固定、一端自由且受截切力作用的可伸长非线性梁结构的非线性边界稳定的能量耗散性。Do[11]提出了可大范围运动的Euler-Bernoulli梁在常见边界条件下的边界稳定控制器设计方法，并进行了适定性与稳定性分析。Wozniak等[12]分析了旋转Timoshenko梁在与其固定的驱动电机的角加速度控制下的稳定性，找到使得系统稳定裕度最大的最优阻尼系数。将帆板等柔性部件视作分布参数对象，边界控制方法可以用于柔性航天器的主动振动抑制。Li[13]考虑了由中心刚体与弹性梁组成的柔性航天器的姿态机动问题，根据非线性耦合动力学系统，通过线性反馈得到中心刚体上的控制力矩，实现大角度姿态机动与振动抑制。He等[14]将带有两个柔性太阳能帆板的卫星等效为中心刚体与两个Euler-Bernoulli梁的组合体，通过对中心刚体施加控制实现两块帆板的振动抑制。Zuyev等[15]考虑了刚体与Kirchhoff板组成的多体力学系统在3个独立控制力矩作用下的非线性控制问题。

对于空间太阳能电站等大型柔性空间结构，在发生大挠度变形从而几何非线性形变不可以忽略的情况下，将弹性运动视作对刚体运动的扰动[1-3]或者仅考虑小应变的耦合动力学模型[5]均难以描述几何非线性引起的动力学刚化现象。因此，本文将空间太阳能电站近似为平面内运动的非齐次自由边界非线性变形梁结构，建立同时考虑全柔性航天器全局刚体运动和局部弹性运动耦合的空间连续动力学控制系统模型，采用端点配置推力器与控制力矩陀螺的控制构型，利用自由边界非线性梁的边界控制方法设计姿态稳定与振动抑制控制器。文章内容安排如下：第1节针对空间太阳能电站动力学系统，给出考虑大范围运动、大变形及边界控制输入项的连续系统模型；第2节基于能量耗散原理，设计全柔性航天器姿态稳定与振动抑制的边界控制器；第3节通过数值求解算法，对全柔性航天器动力学控制方程进行数值仿真，以验证所设计的边界稳定控制律的有效性；第4节给出文章的结论。

1 空间太阳能电站的连续体动力学控制方程

如图1(a,b)所示，将全柔性空间太阳能电站近似为平面内运动的自由边界均匀梁结构，采用混合坐标法，考虑平动、转动与弹性运动的耦合。具体地，采用两端自由的有限变形梁近似全柔性太阳能电站的动力学特性，假设弹性运动满足线性应力应变关系，考虑径向弹性变形与横向弹性变形的耦合，弹性变形量取值于梁的刚柔耦合运动相对刚体运动的商空间，采用线性约束方式确定浮动坐标系。

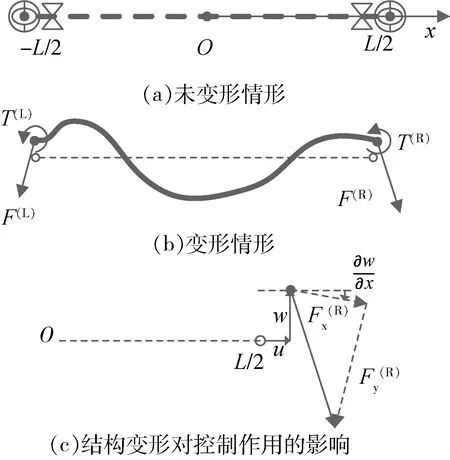
图1 自由弹性结构示意图

1.1 坐标系的选取与运动学描述

(1)

即认为未变形的“刚性”梁质心与实际变形后的梁的质心重合，姿态为变形梁的中性线的方向的平均值。

图2 坐标系与位形变量示意图

1.2 连续体动力学方程

当考虑结构变形对输入的耦合作用时，如图1(c)所示，需要对u∂X(·,t)中的推力器和控制力矩陀螺两类输入项按照所在位置处的位形变量进行变换。

记h、b、ρ、m和E分别为梁的厚度、宽度、密度、质量和弹性模量，J为梁未变形情况下的转动惯量。考虑由梁结构的几何非线性引起的径向弹性变形与横向弹性变形的耦合，采用Hamilton原理，建立平动、转动与弹性运动耦合的空间太阳能电站动力学模型。这里略去动力学推导过程，直接给出整理后的动力学模型。

x(t0)=[[rx0ry0θ0] [vx0vy0ω0]
[u0(·)w0(·)] [vu0(·)vw0(·)]]T
∈SE(2)×se(2)×XKn1/2×XK1/4

(2)

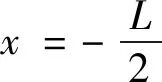
(3)

其中，动力学方程式(2～3)中的相关符号、变量与变量所在空间、空间上的算子的说明如下。

1.2.1 符号说明

上标“·”表示相应变量对时间的导数，上标“T”表示转置；、、、分别表示相应指标的Hilbert空间、Lebesgue可积函数空间、Banach空间、连续函数空间，其上的内积与范数由自然的能量函数的二次型部分确定；Ker、Dom分别表示映射的零空间与定义域。

1.2.2 相关的变量与函数空间

动力学方程式(2～3)中，状态变量的各分量的定义及所属函数空间为

xr=[rx|ry|θ]T∈2(t0,tf;SE(2),se(2),se*(2))

(4)

(5)

(6)

(7)

其中，SE(2)表示刚体位形空间的二维欧式变换群，se(2)与se*(2)分别是与SE(2)对应的速度、角速度与力、力矩的李代数及其对偶空间，πSE(2)是与约束关系式(1)一致的自然投影映射

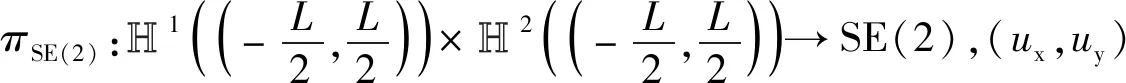
(8)

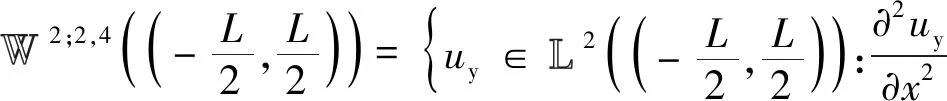
(9)

Banach函数空间的商群定义与Hilbert函数空间的情形类似。

(10)

这里，

(11)

(12)

通过映射πse*(2)对推力器与控制力矩陀螺产生的整体刚体运动效应和局部弹性效应进行分解。即推力器与控制力矩陀螺输出的“合”推力与力矩为

(13)

其中，

(14)

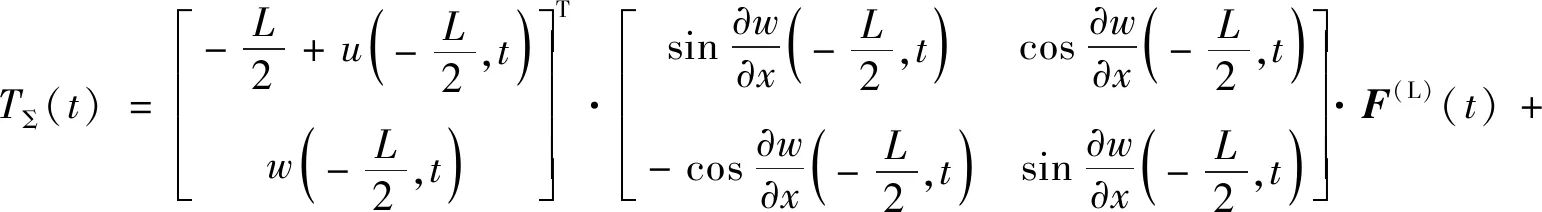
(15)

推力器与控制力矩陀螺输出的“净”应力与弯矩为

(16)

其中，应力与弯矩的内部分量为

(17)

应力与弯矩的边界分量为

(18)

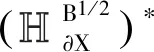
1.2.3 相应的算子

与刚体运动对应的质量矩阵为

Mr=diag(m,m,J)

(19)

(20)

动力学方程中的1表示相应空间上的单位映射，1的维数根据对应元素确定，这里为了表达的简洁性统一表示为1。

(21)

(22)

(23)

(24)

(25)

GK[fx,fy,τ]T=[ux,uy]T

(26)

与

(27)

相互等价。借助GK，可以将非齐次边界问题转化为齐次边界问题。

(28)

边界微分算子的非线性部分

2.4 糖尿病患者握力与体格指标、生化指标的相关性分析 Pearson相关分析发现：无论是男性还是女性，糖尿病患者的握力与其BMI、腰围、清蛋白、总蛋白、肌酐、NRI呈正相关（P＜0.05），与年龄、糖尿病病程、糖尿病并发症数量、其他代谢性疾病数量、空腹血糖、餐后2 h血糖、胰岛素抵抗指数呈负相关（P＜0.05）。见表2。

(29)

(30)

(31)

(32)

2 全柔性航天器边界稳定控制

对于梁结构而言，边界控制指执行机构安装在梁的两端。常见的弹性结构边界控制主要是通过速度反馈引入耗散项，依靠连续体动力学的空间传递作用，使得弹性结构振动发生衰减。

2.1 边界控制问题描述

全柔性航天器的边界稳定控制问题是指，给定初值x(t0)，通过设计基于状态反馈的边界稳定控制器

u∂X(·,t)=f(x(t))

(33)

即

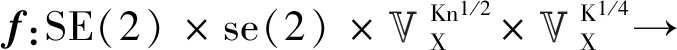
使得动力学控制系统(2～3)满足

(34)

(35)

(36)

2.2 控制器设计

根据自由边界梁在边界处的平动与转动速度，施加满足全柔性航天器整体能量耗散关系的作用力与力矩，使得航天器按期望状态运行。根据动力学方程，可以选择控制律

(37)

(38)

(39)

(40)

其中，

(41)

(43)

(44)

CFL、CTL、CFR和CTR是相应维数的控制参数矩阵。

2.3 稳定性分析

全柔性航天器的能量泛函

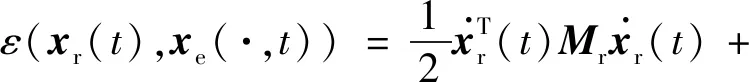
(45)

当选择如式(37～44)所示的控制律时，求取能量泛函的时间导数

(46)

其中，当且仅当在由式(34)确定的相对平衡点处，等号成立。

因此，全柔性航天器在控制律式(37～44)作用下，收敛于相对平衡点。

3 数值仿真与分析

对全柔性航天器动力学控制方程进行数值仿真，以验证所设计的边界稳定控制律的有效性。采用有限元方法对连续动力学边界控制系统进行空间离散化，使用对角隐式Runge-Kutta方法对耦合的姿态分量和弹性运动分量进行时间离散化，得到具有鞍点结构特点的非线性代数方程组；再采用零空间法通过Newton-Krylov迭代方法求解鞍点问题。

3.1 数值仿真参数

全柔性航天器动力学控制方程的相关仿真参数如表1所示。

表1 仿真参数值

对于给定的状态初值，分别计算不施加控制与在t=60s时引入如式(37～44)所示的边界控制作用2种情形下的动力学响应。

3.2 数值仿真结果

在t=60s时引入边界控制作用时，全柔性航天器端点与中点位置的角速度曲线如图3(a)、3(c)与3(b)中实线所示，位于两个端点的沿轴向和横向的推力器以及控制力矩陀螺的输出如图4(a)、4(b)及4(c)所示。

图3 全柔性航天器端点与中点处的角速度曲线

图4 全柔性航天器在边界控制作用下的推力器与控制力矩陀螺输出值曲线

3.3 仿真结果分析

由图4发现，因为全柔性航天器的一阶挠度方向振动在弹性运动中起主导作用，由边界控制得到的两端轴向推力器输出的推力、控制力矩陀螺输出的力矩相位相反，挠度方向的推力器输出的推力相位相同。两个端点处沿挠度方向的推力器输出的推力几乎相同，说明全柔性航天器的低速旋转整体运动对于局部弹性运动的影响不明显。这里更关注的是轴向、横向推力器输出值的相对大小，由于仿真参数没有对应实物的尺寸与性能参数，在分析具体的被控对象时，需要考虑适当的尺度变换，以利用本文所给出的全柔性航天器边界稳定控制问题的分析与设计结果。