单位圆在三角函数教学中的作用

郭芳丽

(陕西省咸阳师范学院附中 712099)

在初中，我们利用直角三角形学习了锐角三角函数；到了高中，为进一步研究任意角的三角函数，需要借助单位圆.单位圆简单直观，具有圆的对称性和旋转不变性，三角函数有了单位圆的加入，便展开了一系列行之有效的教学活动.

1 理解弧度制

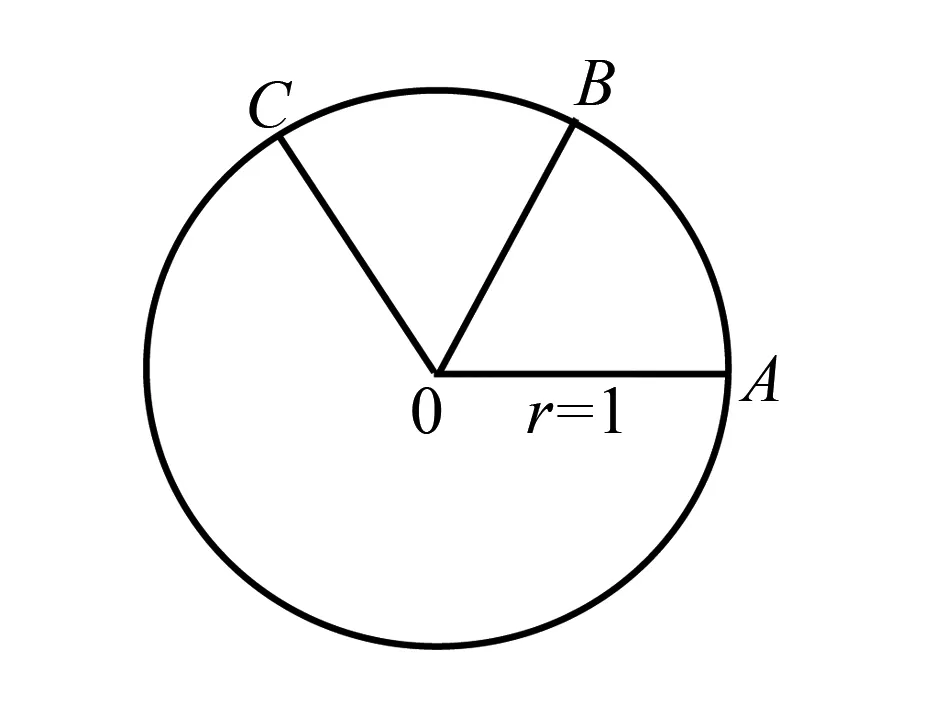
图1

在讲解角的集合与实数集对应关系的过程中，引入(如图2所示)单位圆模型：让单位圆M与数轴相切于原点O，把数轴看成一个皮尺， 对于任意一个正数a，它对应数轴上的点A，把线段OA逆时针方向缠绕到单位圆M上，点A对应单位圆上的点A′，这样以MO为始边，经逆时针方向旋转以MA′为终边的圆心角α的弧度数为正数a；同样对于任意一个负数b，对应数轴上的点B，将线段OB顺时针方向缠绕到单位圆M上，点B对应单位圆上点B′，则以MO为始边经过顺时针方向旋转以MB′为终边的圆心角β的弧度数为负数b.

2 定义任意角的三角函数

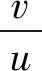
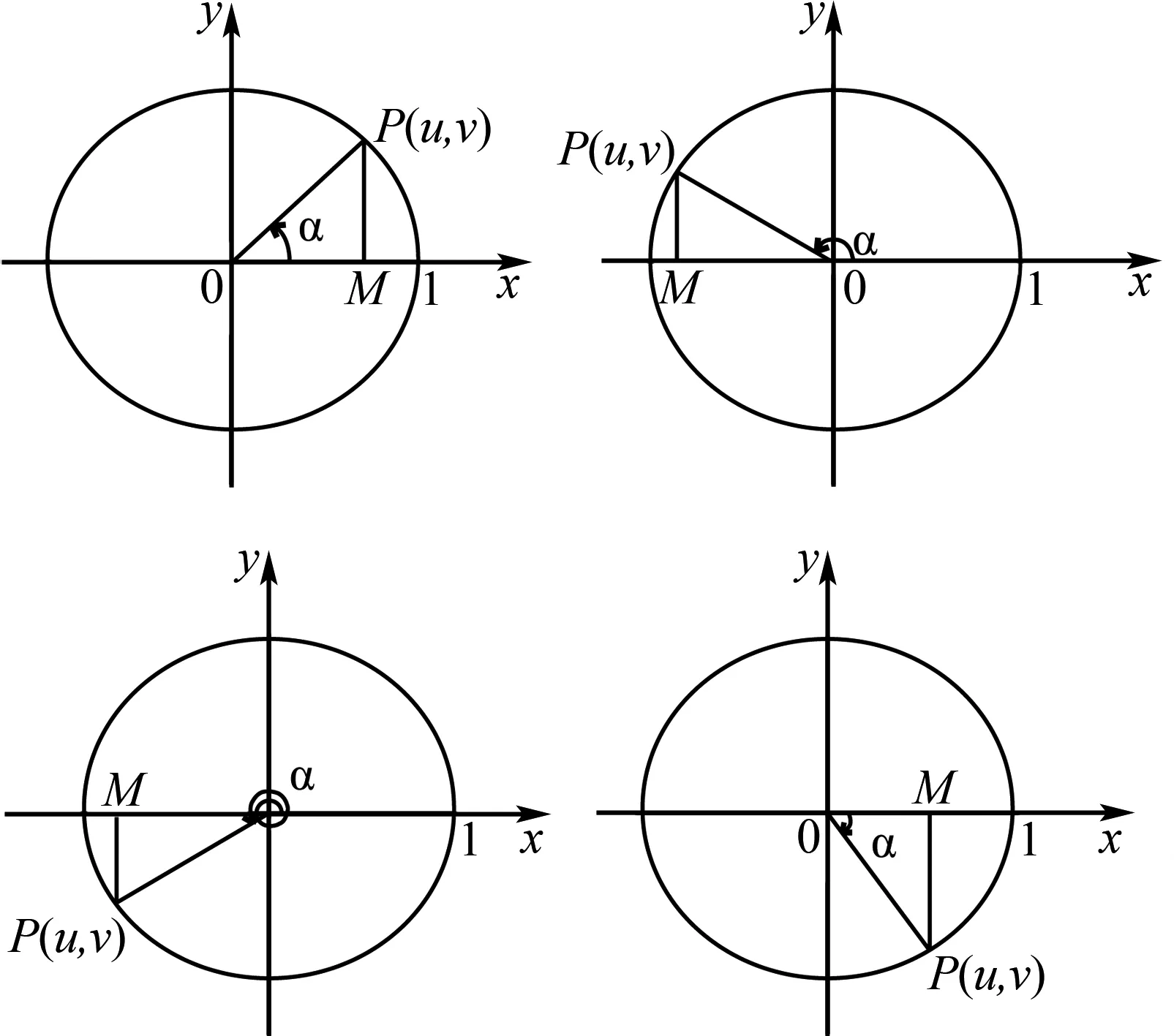
图3

3 推导诱导公式

利用单位圆的对称性与几何直观易得：

(1)角α与-α的终边关于x轴对称，终边与单位圆交点的横坐标相等，纵坐标互为相反数(图4)，即cos(-α)=cosα=u,sin(-α)=-sinα=-v.

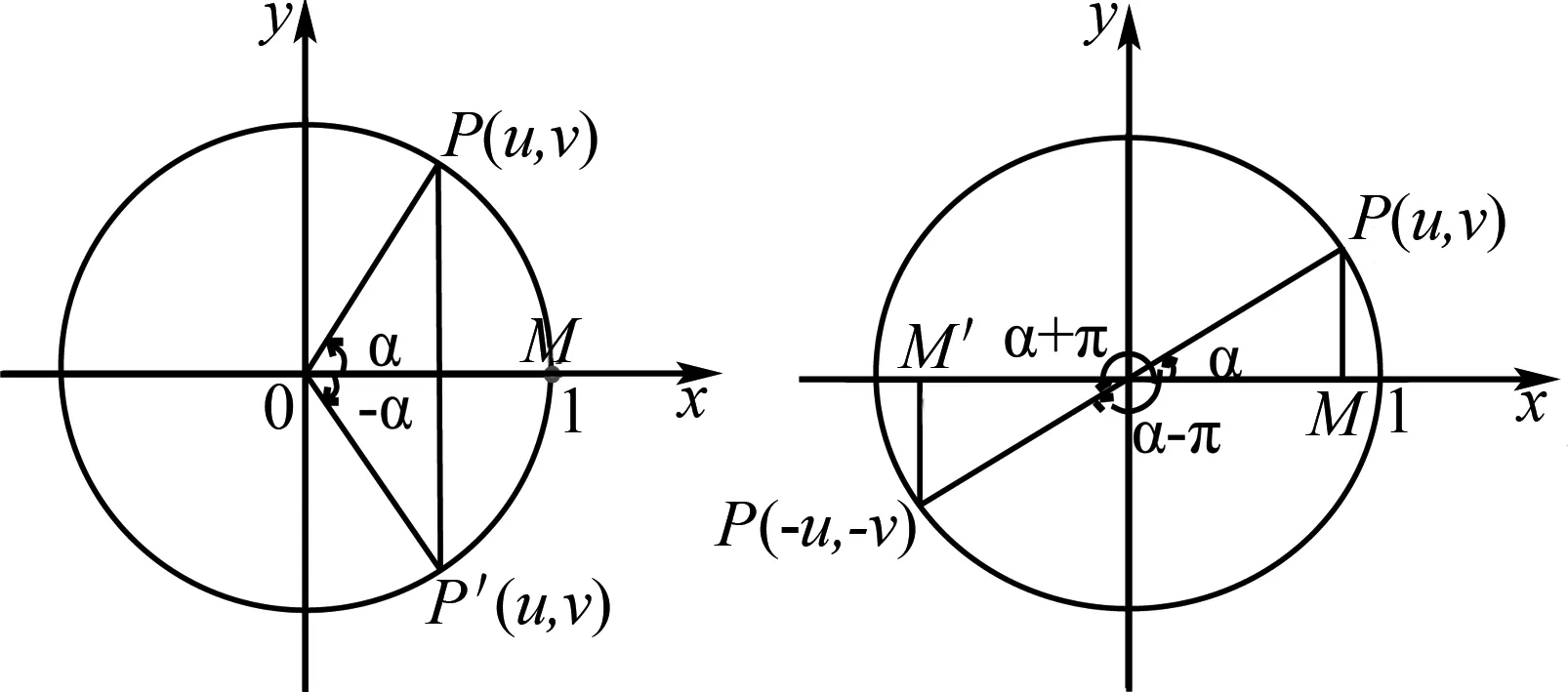
图4 图5

(2)角α与α±π的终边关于原点对称，终边与单位圆交点的横、纵坐标均互为相反数，即cos(α±π)=-cosα=-u,sin(α±π)=-sinα=-v(图5).

(3)角α与π-α的终边关于纵轴对称，终边与单位圆交点的横坐标互为相反数，纵坐标相等，即cos(π-α)=-cosα=-u,sin(π-α)=sinα=v(图6).

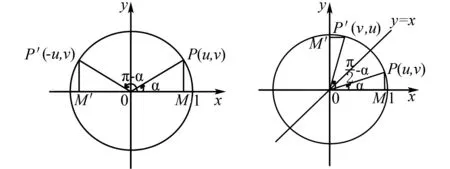
图6 图7

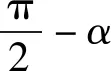
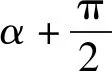
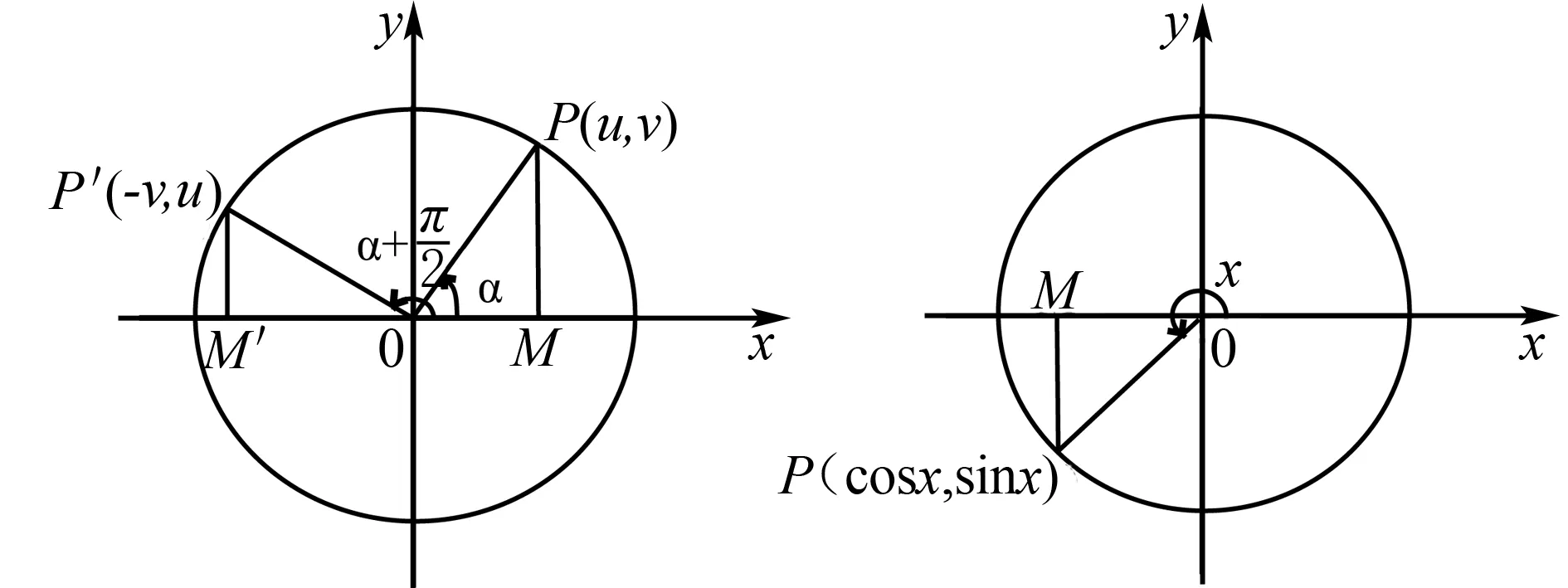
图8 图9

4 研究三角函数性质

如图9，在给定的单位圆中，设任意角x的终边与单位圆交于点P(cosx,sinx)，当自变量x变化时，点P的横、纵坐标也在变化.根据正弦函数y=sinx和余弦函数y=cosx的定义，易知以下基本性质：

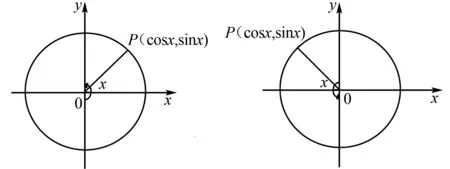
图10

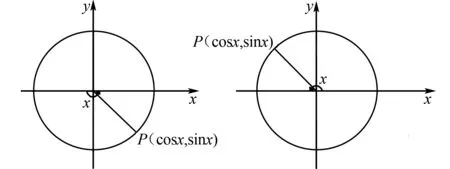
图11

5 绘制三角函数的图象

(1)先作出三角函数线：在图12中，设单位圆与任意角α的终边交于点P，过点P作x轴的垂线，垂足为点M，过点A(1,0)作x轴的垂线，与角α的终边或终边的反向延长线交于点T，则有向线段MP,OM,AT就是角α的正弦线、余弦线和正切线.

图12

(2)再借助正弦线和正切线绘出正弦函数和正切函数在一个周期内的图象(图13).

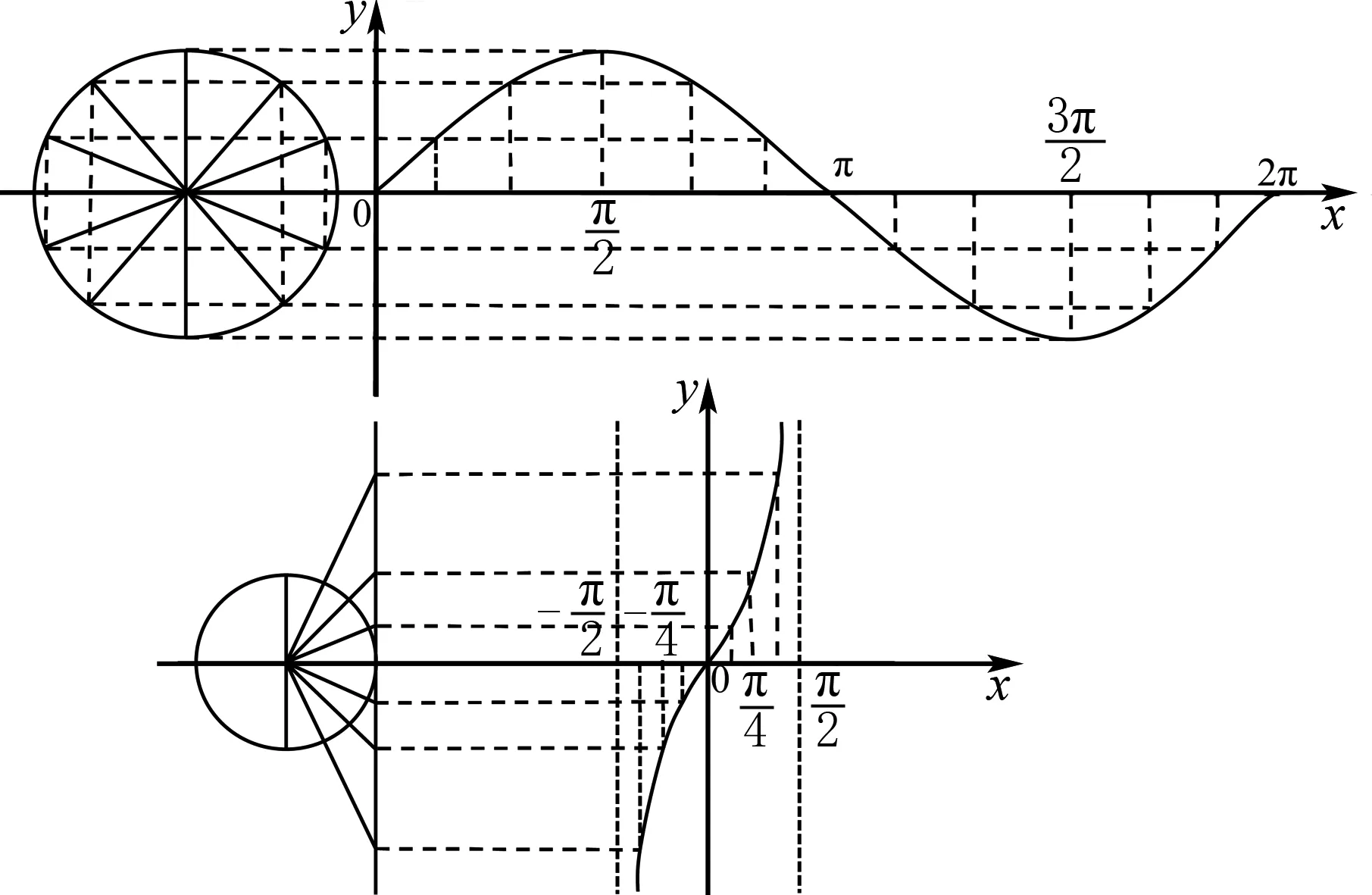
图13

6 证明同角三角函数关系

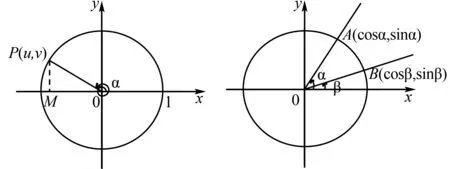
图14 图15

7 推证两角差的余弦公式

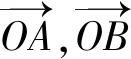
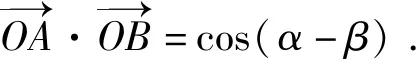
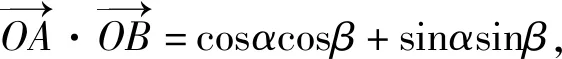
所以cos(α-β)=cosαcosβ+sinαsinβ.

总之，将单位圆融入三角函数教学，不仅有很好的辅助借鉴意义，还事半功倍.