高中阶段的排列组合问题
2022-11-03梁佳殷
梁佳殷
(黑龙江省哈尔滨师范大学教师教育学院 150025)
1 特殊元素和特殊位置
这类问题的主要特征是具有特殊元素或者特殊位置.这时我们应优先安排它们的位置.
例1由0,1,2,3,4,5可以组成多少个没有重复数字的四位奇数?
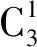
2 元素之间相邻
这类问题的主要特征是有某几个元素必须相邻.这时我们先将它们捆绑在一起,视为一个元素,先求捆绑外部的排列,再求捆绑内部的排列,称为捆绑法.
例2A,B,C,D,E,F,G七个人站在一排拍照,其中A,B,E三人想站在一起,D,G二人想站在一起,求一共有多少种不同的站法?

3 元素之间不相邻
这类问题的主要特征是有某几个元素必须不相邻.这时我们可以先将没有特殊要求的元素进行排列,再将必须不相邻的元素进行插空,称为插空法.
例3 (改自2021年理科甲卷10)将4个1和2个0随机排成一行,若2个0不相邻,共有多少种不同的排法?
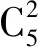
4 元素之间顺序固定
这类问题的主要特征是有某几个元素的前后顺序固定,这时我们共有三种做法.其一,先将其他元素安排进空位中,再考虑顺序固定的几个元素;其二,先将顺序固定的几个元素列出,用其他元素进行插空;其三,对所有元素进行全排列,再除去顺序固定元素的排列数.
例4学校迎新晚会共有A,B,C,D,E,F,G七个节目,考虑到节目效果,节目G必须在节目A之前,节目A必须在节目D之前,求一共能安排多少种不同的节目顺序?
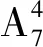
解法2 先将顺序固定的几个元素列出,由于其顺序固定,只有1种排法,即GAD,再将剩余的4个元素进行插空,放入第一个元素时有4个空位,放入第二个元素时有5个空位,放入第三个元素时有6个空位,放入第四个元素时有7个空位,由分步乘法计数原理可得,共有1×4×5×6×7=840种不同的节目顺序.
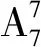
5 分配问题
这类问题的主要特征是将元素分配到不同的位置中,且每个位置要求至少有几个元素.这时我们先按照要求进行选择,再进行分配.
例5将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( ).
A.60种 B.120种 C.240种 D.480种
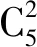
6 分组问题
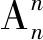
例6将A,B,C,D,E,F,G七个人分为3组,一组3个人,另外两组2个人,求共有多少种分法?
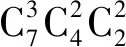
7 元素相同问题
这类问题的主要特征是元素之间没有任何区别,再将它们进行分组,且每组至少一个元素.这时我们先将全部元素列出,以插板的方式将其分组,即用(m-1)个隔板将全部n个相同元素分为m段,称为隔板法.
例7把10个相同的小球放入7个不同的盒子中,每个盒子至少放1个球,共有几种不同的放法?

8 复杂问题
之所以称为复杂问题,是因为这类问题一般都不太容易理解,给的条件很复杂,学生在遇到这种题后第一反应一般是分类,就很容易出现多算、漏算的现象.这时我们可以将问题转化为上述7类问题中的一种便于解答.
例8现有排成一排的十把椅子,若A,B,C,D四人都要入座,且每个人的左右两边都想留有一个空位,则一共有多少种不同的坐法?
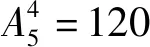
9 分情况讨论问题
这应该是学生最喜欢的一类问题,没有什么特殊的技巧和解法,仅是讨论各种可能的情况就能够得出答案.
例9现要求在4名男生和3名女生中选择4人作为班会的主持人,且要求必须有男生也有女生,求有多少种不同的选法?

注:有时运用穷举法或者画树状图的方式,可能会得到意想不到的效果.
10 染色问题
染色问题是一种复杂的分情况讨论问题,做法一般是先选择其中一个位置,再跳格进行讨论.

图1
例10如图1,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,现在要求在花坛的每一块都要种且只能种1种花,且相邻的2块所种的花颜色不能相同,则不同的种法总数为____.
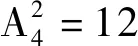
这类问题也存在着通解,若一个圆被分为n个扇形,想用m种不同的颜色进行染色,每个小扇形只能染一种颜色且相邻的两个扇形颜色不能相同,则其共有(m-1)n+(-1)n(m-1)种不同的染色方法.
排列组合这一节对学生的数学建模、数学运算、逻辑推理等核心素养要求较高,但只要多加练习,能够认准题型并熟练运用对应的方法,注意细节,就可以轻松解决.
