无限路及其笛卡尔积、直积的孪生α-距离边染色

杨 环

(海口经济学院 聚星数字经济学院，海南 海口 570100)

0 引言

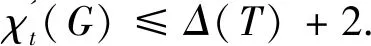
在孪生边染色概念基础上，可以定义以下更一般的带有限制条件的边染色概念.

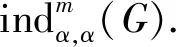
在定义1中，孪生1-距离边染色也叫孪生边染色.因2-距离边染色也称为强边染色[4]，所以孪生2距离-边染色也称为孪生强边染色[5].

引理1 设G是阶至少为3的简单图,且G的连通分支为G1,G2,…，Gω，有

本文主要研究无限路的孪生强边染色，以及无限路的笛卡尔积、直积的孪生边染色，文中未说明的符号及术语可参见文献[6]与[7]．

1 主要结果

设P∞为无限路，且V(P∞)=Z(Z为整数集),其中V(P∞)中任意不同顶点i与j相邻当且仅当

|i-j|=1．设CP(d)与DP(d)分别为d个无限路的笛卡尔积与直积，并分别记为CP(d)=P∞□P∞□…□P∞与DP(d)=P∞∧P∞∧…∧P∞，且它们的顶点集为V(CP(d))=V(DP(d))={(x1,x2,…，xd)|xi∈Z,i=1,2,…,d}，其中d≥2.

关于无限路的孪生强边染色，有以下定理1及证明.

首先,验证σ是P∞的2-距离边染色.显然,P∞中彼此距离不超过2的边最多有3条.任取P∞的距离不超过2的3条边e=vivi+1，e＇=vi+1vi+2与e″=vi+2vi+3.由σ的定义可知，σ(e)=(i)3，σ(e')=(i+1)3，σ(e″)=(i+2)3.显然e，e＇，e″具有不同的颜色，所以σ是P∞的2-距离边染色.

其次,验证由σ诱导的点染色σ＇是P∞的2-距离染色.

任取P∞中距离不超过2的三个顶点vi，vi+1，vi+2.由σ及σ＇的定义可知，σ'(vi)=(2i+2)3，σ'(vi+1)=(2i+1)3，σ'(vi+2)=(2i)3.显然，σ'(vi)≠σ'(vi+1)，σ'(vi)≠σ'(vi+2)，σ'(vi+1)≠σ'(vi+2).否则，可推出矛盾：0=1，或1=2，或0=2.因此，P∞中距离不超过2的点在σ＇下染不同的颜色，即σ＇是P∞的2-距离染色.

由以上分析可知，σ是P∞的一个3-孪生强边染色.

关于Cp(d)的孪生边色数，有以下结果：

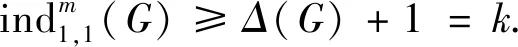
设ei=(x1,x2,…，xi，…，xd)(x1,x2,…，xi+1，…，xd)，对每一i=1,2,…d，令

显然，σ所用颜色数为k.下面证明σ是G的正常边染色，且由σ诱导的点染色σ＇是G的正常点染色.

首先,证明σ是G的正常边染色.设uv与vw为G的任意相邻两边，其中

v=(x1,x2,…，xi，…，xd),u=(x1,x2,…，xi+θ1，…，xd),u=(x1,x2,…，xi+θ2，…，xd).

且θ1=±1，θ2=±1.由σ的定义知，

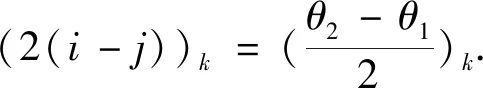
其次，验证由σ诱导的点染色σ＇是G的正常点染色.

对G中每一顶点v=(x1,x2,…，xd)，其邻边有2d条.由σ与σ＇的定义知，

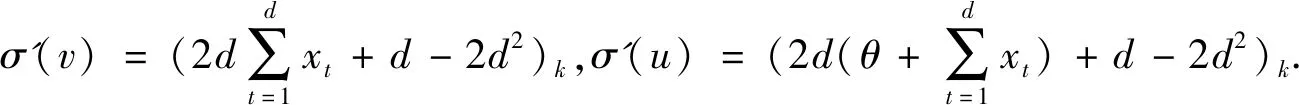
显然，σ'(v)≠σ'(u)，否则，(2dθ)k=0，这与θ=±1，k=2d+1矛盾.因此，σ＇是G的正常点染色.

由以上分析可知，σ是G的一个(2d+1)-孪生边染色.

为研究DP(d)的孪生边染色，首先给出以下两个引理：

引理2 设G是局部有限无限图.若G存在k-边染色(或k-孪生边染色)，则G∧P2存在k-边染色(或k-孪生边染色).

证明设P2的顶点集为{0,1}，并设颜色集合为{0,1,…，k-1}.

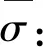
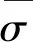
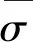
其中E*=E(G∧P2),E=E(G).

任取G∧P2的两个相邻顶点(x,0)与(y,1)，则

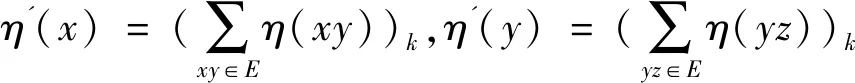
引理3 对任意正整数d，有χ＇(Dp(d))=2d，其中χ＇(Dp(d))表示Dp(d)的边色数.

证明用数学归纳法证明.当d=1时，Dp(1)=P∞，显然，χ＇(Dp(d))=2d.假设当2≤d≤k时定理结论成立.现在证明χ＇(Dp(d+1))=2d+1.由图直积的定义知，Δ(DP(d+1))=2d+1.所以χ＇(Dp(d+1))≥2d+1.为证明χ＇(Dp(d+1))≤2d+1，下面构造DP(d+1)的一个(2d+1)-边染色.

由归纳假设，可设σ为DP(d)的一个2d-边染色,其中颜色集合为[2d]0.现在，对DP(d+1)的每个子图Hi进行边染色.具体地，若DP(d)中顶点x=(x1,x2,…，xd)与y=(y1,y2,…，yd)相邻，则令

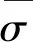
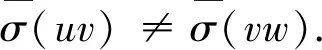
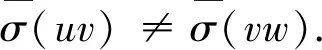
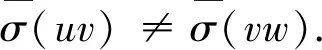
关于DP(d)的孪生边染色,有以下定理3.

证明用数学归纳法证明.当d=2时，显然，DP(2)可表示为两个不相交的CP(d)之并.

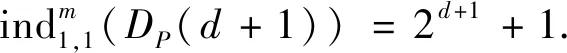
首先，由归纳假设，DP(d)存在(2d+1)-孪生边染色，根据引理2，DP(d)∧P2存在一个(2d+1)-孪生边染色，记为σ0，所用颜色集为[2d+1]0.由引理3，DP(d)存在(2d)-边染色，由引理2，DP(d)∧P2存在一个(2d)-边染色，记为σ1，所用颜色集为[2d+1+1]0-[2d+1]0.