关注高频易错点 打造品质新课堂——以三角函数的图象与性质为例

章莹莹

(江苏省新海高级中学 220006)

三角函数图象与性质是近年高考中的高频考点，高中学生在处理有关三角函数问题时，常因对三角函数的图象与性质的理解不够到位和缺乏严谨而又深入的思考导致错误.笔者着重从以下几个方面，就三角函数的图象与性质在具体运用中出现的高频易错点进行详细的归纳整理，旨在帮助同学们进一步提高解题思维能力，避免一些常见差错的产生.

1 忽视三角函数图象的周期性

利用三角函数的图象求解三角不等式时，需要先在一个周期内加以分析，再结合正弦函数、余弦函数的周期2kπ(k∈Z,k≠0)或者正切函数的周期kπ(k∈Z,k≠0)，即可获得原不等式成立的充要条件.

错解由题意可得2cos2x+1≥0.

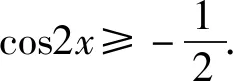
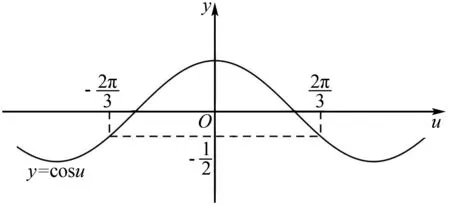
图1

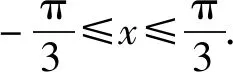
辨析以上错解的原因是利用余弦函数的图象解不等式时，只是在一个周期内进行思考，显然忽视了余弦函数图象本身具有的周期性，导致因考虑不全而出现错误.

正解由题意可得2cos2x+1≥0.

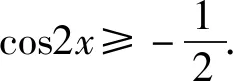
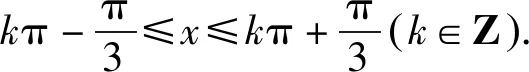
故该函数的定义域为

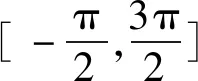
2 忽视区间端点值的取舍问题

求解三角函数中的参数范围问题时，往往会利用转化思想，若先转化为区间之间的包含关系，再据此构建不等式组时，则需要准确分析区间端点值的取舍问题，否则，极易因考虑不全而出现差错.

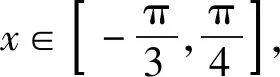
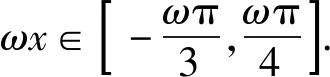
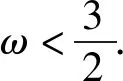
辨析以上错解的原因是构建不等式组时，对区间端点值的取舍理解不到位，会导致缩小参数的取值范围；同时还忽视了对题设已知条件ω>0的及时运用，会导致扩大参数的取值范围.

正解函数f(x)=2sinωx的图象，可根据正弦函数y=sinx的图象经过伸缩变换得到.

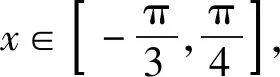
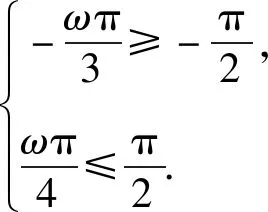
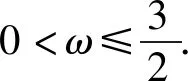
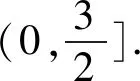
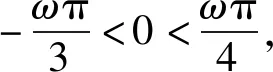
3 忽视正弦函数、余弦函数的有界性

处理与正弦函数、余弦函数有关的取值范围问题时，必须考虑正弦函数、余弦函数的有界性(即|sinx|≤1,|cosx|≤1)在解题中的充分运用；否则，极易因求得的取值范围过大而出现差错.

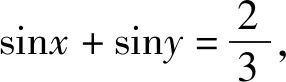
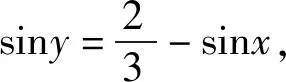
又注意到-1≤sinx≤1，

剖析上述错解中在消去siny时，因忽视siny的有界性对sinx的取值范围的影响，而导致错误.

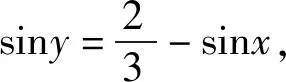
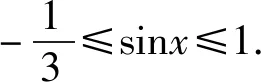
评注本题挖掘隐含条件时，不但要利用sinx的有界性，而且还要利用siny的有界性.显然，只有双管齐下，才能准确获解.

4 忽视正弦函数、余弦函数的单调性

利用已知给定的某角的正弦函数值(或余弦函数值)以及对应的正弦函数(或余弦函数)的单调性，可帮助我们进一步缩小有关“角”的取值范围，从而可帮助我们准确求解有关取值问题，避免差错.

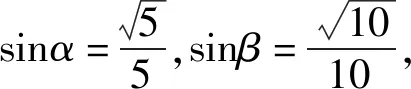
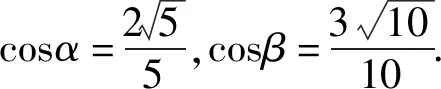
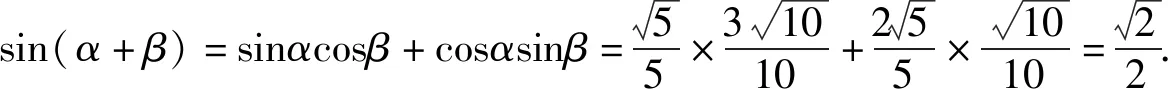
剖析上述错解的根源是没有借助正、余弦函数的单调性，进一步探究角α,β的取值范围，从而因取值范围过大，导致产生了令人难以发现的较为隐蔽的错误！

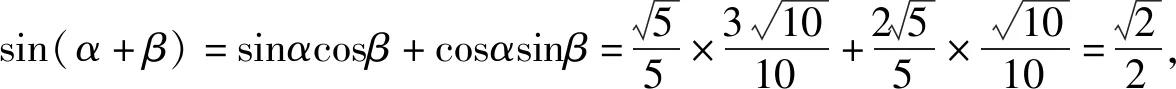
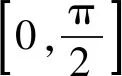
正解2因为α,β都是锐角，

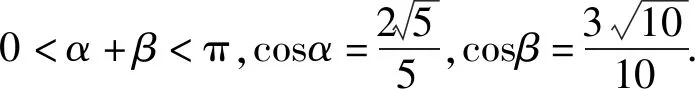
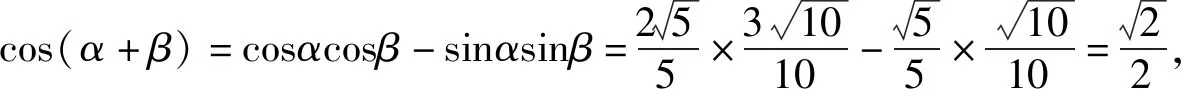
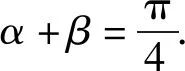
评注本题如果考虑利用正弦值分析(解法1)，则极易出错；如果考虑利用余弦值分析(解法2)，则不易出错.请想一想为什么？

总之，三角函数的图象与性质有着广泛的应用，需要我们结合对典型错解的剖析，掌握解题规律，进一步提高解题的速度和准确性.同时，作为一线教师，我们必须结合自己的教学现状，经常深入研究学生学习中的易错点以及遇到的思维障碍，才能全方位地了解学生的实际情况，对自己的教学过程不断反思，进而改变教学的方式方法，有效提高教学效率，打造品质课堂，落实核心素养.