比较中促思沟通中建构——《解决问题的策略（从条件想起）》单元复习教学设计

文|吴华平 姚凯

【教学内容】

苏教版三年级上册第五单元。

【教学过程】

一、例题再认识

1.课件出示例1。

师：我们拿到问题的第一时间需要干什么？

生：首先我们要读题目。

师：那对于这个问题，你是怎样想的？这里需要先求出什么？

生：先求出第二天摘的个数。

师：根据什么可以求出来？

生：根据第一天摘的个数和以后每天都比前一天多摘5 个，可以求出第二天摘的个数。

（课件出示框两个条件）

师：第二天摘了多少个呢？

生：30+5=35（个）。

师：接下来怎么办？

生：再根据第二天摘的个数和以后每天都比前一天多摘5个，可以求出第三天摘的个数。

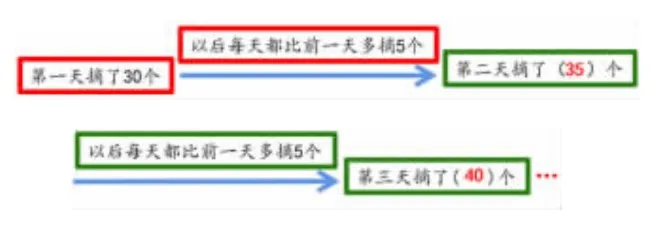
师：如果就这样一直往下想，还可以得到……

生：还可以得到第4 天、第5天……的个数。

师：像这样的思考过程，其实就是分析问题。

师：问题分析完了，接下来可以用哪些方法去解决？

生1：我们可以进行列式解答。（课件出示例题解答过程）

生2：我们曾经借助过列表的方式。（课件出示例题解答过程）

师：列表可以帮助我们更清楚地表示出几天摘桃子的情况。

2.课件出示例2。

师：这个问题你们还记得吗？你又是怎样解决这个问题的？

生：根据绿花有12 朵和黄花的朵数是绿花的2 倍，可以求出黄花的朵数。

生：再根据黄花的朵数和红花比黄花多7 朵，可以求出红花的朵数。

师：要求最后的问题，我们需要从最初的已知条件出发，一步一步地往下想。

师：在解决这个问题时，你们还想到了用什么好方法来表示几个数量之间的关系？

生：这儿出现了好几种花的数量，我们可以画线段图表示。（出示课本线段图）

师：为什么画线段图呢？

生：线段图可以帮助我们把条件和问题看得更清楚。

【设计意图：从学生回忆单元的两个例题入手，经过了单元学习，学生解决问题并没有困难，但很多方法还是碎片的、零散的，需要教师帮助引导他们进行知识的重组与统整。此教学环节，教师重策略再现轻解题过程，重点让学生回忆解决问题的过程，在知识的再认识中让学生进一步感知本单元问题的特征。】

二、比较沟通

1.找不同（课件同时出示例1、例2）。

师：刚刚我们回忆了本单元的两例题的解题过程，比较例1 和例2，他们有什么不同？同桌说一说。

生1：一个有两个条件，一个有三个条件。

师：你是从两道题的“长相”上发现了不同。

生2：例1 的两个条件，有一个条件“以后每天都比前一天多摘5 个”一直都要用到它，例2 三个条件我们要好好找一找根据哪两个条件求出一个问题，然后再根据求的结果和第3 个条件才能求出最后的问题。

师：你是从条件之间的关联上发现了他们的不同。

生3：第1 题用列表比较方便，第2 题画线段图比较方便。

师：你是从我们解决问题时用的辅助方法上发现了不同。

2.找相同。

师：老师想知道，不同的两个问题为什么放在一个单元去学习，它们一定有相同的地方。

（1）小组内交流。

（2）全班交流。

生：都是从条件出发去解决问题的。

师：像这样，从已知条件出发分析和解决问题的方法，是一种常用的解决实际问题的策略。

（3）将两个例题的思路图合并成以下模型。

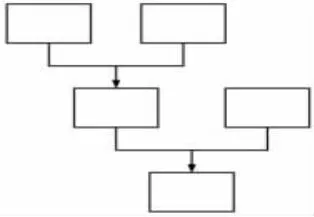
（4）在解题问题的过程中都经历了哪几个过程？

理解题意——分析问题——解决问题——回顾反思

【设计意图：结构化教学需要我们不断帮助学生寻找发现前后知识的关联，只有打通了一些“隔断墙”才能将知识与知识之间织成网结成片。本环节在加深学生对新旧知识的比较中，帮助他们理解解决问题的策略，让学生在不同中找相同便是帮助学生构建从条件想起解决问题一般思路和方法的结构模型。】

三、策略再应用

1.第一层次练习。

武术社团第一周教了10 个招式，以后每一周还要再教4 个新招式。那么到第3 周教了多少个招式？到第4 周呢？

生1：看着刚才的框图我认为可以根据第一周10 个武术动作和每一周还要再教4 个新动作可以求出第二周教了14 个武术动作，再根据第二周教了14 个武术动作和每一周还要再教4 个新动作可以求出第三周教了18 个武术动作。以此类推可以求出第四周教了22 个武术动作。

生2：我也是这样想的，不过我是列表格来写算式的。

2.第二层次练习。

航模社团的人员分布是这样的，你能看着线段图来说一说条件吗？

师：根据这里的条件可以提出什么问题？

生1：二年级有多少人？

生2：三年级有多少人？

生3：一共有多少人？

3.第三层次练习。

在学校组织的绘画展览中，一年级的作品有30 幅，二年级有45 幅，三年级比一、二年级的总数少15 幅，四年级比三年级的2 倍少30 幅。

师：这题涉及到的年级就更多了，那这个时候你觉得可以怎样，把条件变得更加清楚一些呢？

生：可以画线段图。

师：画线段图是一种好的方法，有没有其他方法了呢？

生：可以借助列表格的方式。

师：好，那接下来，我们将这四个年级参加展览的情况分别填到表中，一起看一看。

师：除了我们刚刚解决的三年级和四年级参加展览的问题，还可以解决哪些问题呢？

【设计意图：三个不同层次的练习，让学生不仅仅停留在模仿例题去解决问题，更重要的是让学生在整理复习后能真正将知识系统化、结构化，通过不同层次的练习把握各类看似不同其实解题方法相同的数学问题，从而内化解决问题的方法。】