加强概念变式增进概念理解——《梯形的认识》素养进阶习题展评与教学建议

文|章威维 陈楚楚 宋煜阳

一、习题展评

●习题一

1.习题内容。

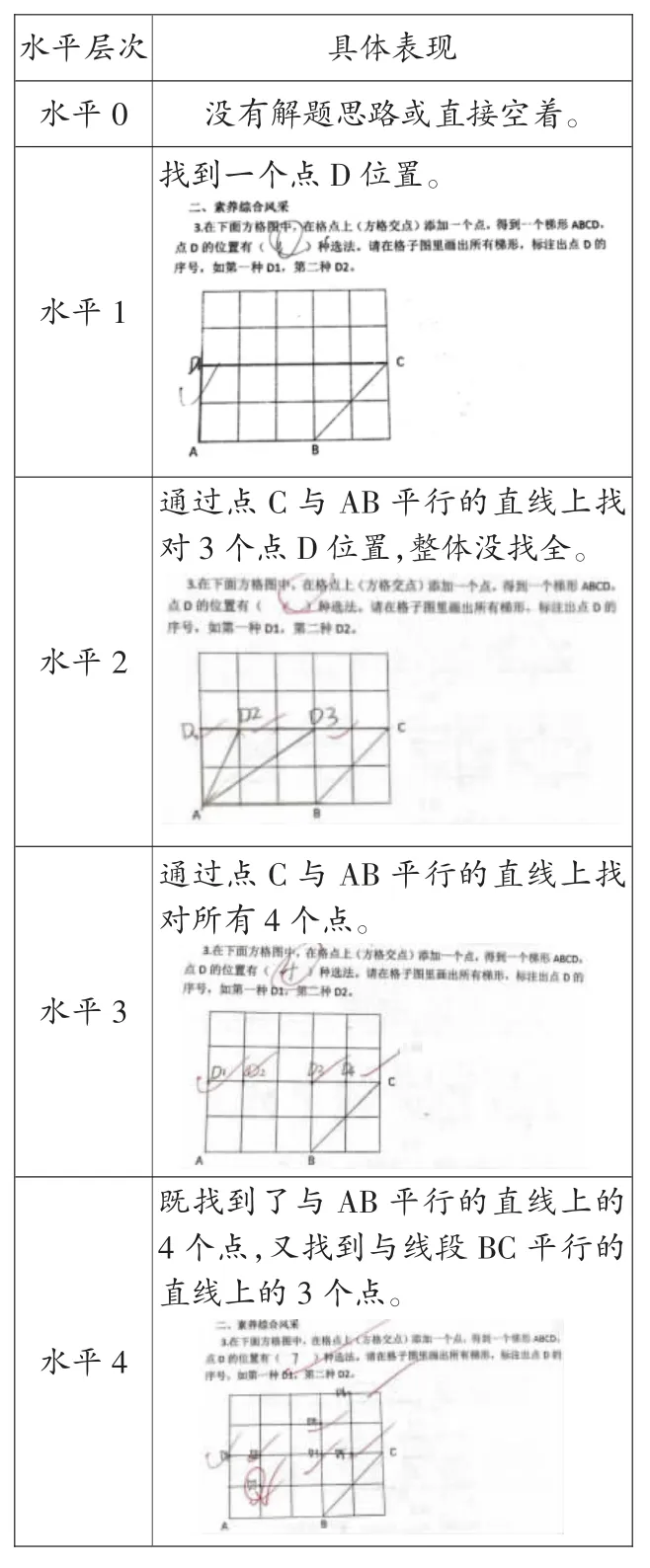
在下面两个图形中分别添加一条线段，使它形成梯形。（每个图形各画四个）

图1

图2

说一说：图1 改画为梯形，你是怎样想的？_______________。

图2 呢？_______________。

2.能力指向。

对梯形定义的理解。通过梯形的分割活动，考查学生对梯形概念的了解程度。要形成梯形，在没有平行线的图形中，需要创造出一组平行线；在平行四边形中需要破坏一组平行线，使图形只有一组平行线，强化“只有一组对边平行”的定义理解。

3.学情分析。

对乡镇小学39 名学生进行了后测，发现一半以上的学生对图1 能画出2、3 个梯形，图2 基本能画对。图1 中58.9%的学生画出与线段a 构成一组平行线的梯形，38.5%的学生画出与线段b 或线段d 构成一组平行线的梯形，只有12.8%的学生画出与线段c构成一组平行线的梯形。可见学生对一般四边形中分割出梯形，有需要创造出一组平行线这样的意识，但对平行线的方位，还是趋向于水平方向的最多。69.2%的学生无法清楚地写出“说一说”中画出梯形的依据，只会根据图形描述成：“把四边形分割成一个梯形和三角形”，不能从梯形的概念去说明如何从一般四边形或平行四边形中分割出梯形。

●习题二

1.习题内容。

在下面图形中任选两个图形进行随意交叉摆放，重叠部分会形成不同形状的图形。按要求选择合适的序号并画出草图。

2.能力指向。

对各个图形特征的掌握与应用。通过两个图形交叉后重叠部分图形的判断，考查学生对图形特征的认知，发展学生的动态想象能力。

3.学情分析。

测评统计显示，试测班级中12.8%的学生能全部正确解答，但大部分的学生只能回答正确（1）（2）（3）小题，解答两个图形重叠部分是六边形出现困难。错例中部分学生画成了五边形，如下图。

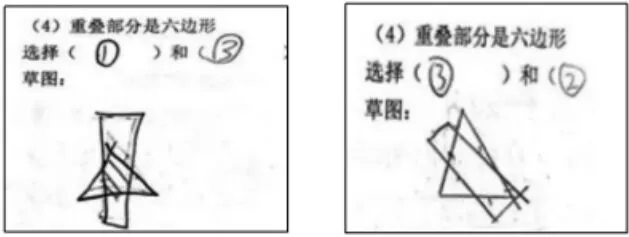
这个错误体现出学生缺少对不规则多边形图形的认知。学生平时常见的图形都是规则的图形，如六边形常见的是正六边形的图示，但对不规则六边形学生就不敏感，已有认知经验的缺乏导致解题困难。

●习题三

1.习题内容。

在下面方格图中，在格点上（方格交点）添加一个点，得到一个梯形ABCD，点D 的位置有（）种选法。请在格子图里画出所有梯形，标注出点D 的序号，如第一种D1，第二种D2。

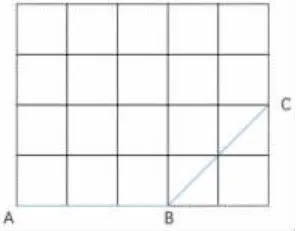
2.能力指向。

对梯形概念变式和梯形特征的辨析。根据三个点找第四个点形成梯形，在动点的移动中，考查学生对梯形概念的理解和特征的掌握，发展学生的空间观念。

3.学情分析。

根据学生解答的具体表现，划分为五个水平层次，如下表。（表格见文末）

测试班级学生的水平大多集中于水平1、水平2 和水平3。问题主要反映为概念变式认识不充足，局限于标准梯形（两底水平方向）和直角梯形等特殊梯形的认知，对一般梯形（两底不在水平方向或两腰接近平行）辨认度低。60%的学生能找到形成直角梯形的点D；43.5%的学生能找到与AB 边平行的线段DC 上的三个点，还有20%的学生错误地把形成平行四边形的那个点也标进去了。另外的三个点，需要调用与BC 边平行的线段认知经验，学生明显碰到了困难，只有15.6%的学生能找到其中的1、2 个点，达到水平4 的不足6%，说明对梯形概念特征的灵活辨析能力还不足。

二、教学建议

1.在操作和辨析中，建构图形特征，强化概念理解。

在建立标准梯形的表象时，学生对于“两条底不在水平方向”或“两条腰接近平行”这些非标准图形的一般梯形，容易出现辨识困难，需要通过变式材料的操作、辨析帮助学生建构概念。教学中，一方面通过画不同梯形的活动，在比较中凸显梯形的本质属性；另一方面通过变式图形辨析活动，引导学生从形和边这两个角度去判断，以强化梯形的特征。像习题一添加线段的过程中，在一般四边形中努力找出一组平行线，建立“没有平行线的四边形需要创造一组平行线”的操作经验；而在平行四边形中，则需要破坏一组平行线，使它们不平行。这样的操作，都指向“只有一组对边平行的四边形是梯形”这一概念本质理解。

2.在分割和移动中，加强图形联系，发展空间观念。

在四边形概念体系中，梯形与其他四边形的关系非常密切。需要打通各图形之间的联系壁垒，通过分割或移动，建立梯形与其他图形的联系。如，移动梯形的上底，当上底与下底一样长时，就变成了平行四边形；当上底为零时，就变成了三角形。又如，在一个梯形中画一条线段，既能分割成平行四边形和梯形，也能分割成两个三角形，还能分割成两个梯形或一个梯形和一个三角形等。这些分割和移动，有效沟通了梯形与其他图形的关系，培养和发展了学生的动态想象能力。教学中，可以动态演示一个梯形，随着一个点的不断移动，从“标准梯形——等腰梯形——直角梯形——平行四边形——两腰接近平行的梯形——三角形”进行转变，图形的变动引发了特征的变化，促使学生对梯形与平行四边形、三角形之间的内在联系理解更为清晰。