基于多阶段退化建模的谐波减速器实时可靠性评估与寿命预测

王国锋，曹增欢，冯海生，王俊奇，户满堂

基于多阶段退化建模的谐波减速器实时可靠性评估与寿命预测

王国锋1，曹增欢1，冯海生2，王俊奇2，户满堂1

(1. 天津大学机械工程学院，天津 300350；2. 埃夫特智能装备股份有限公司，芜湖 241007)

谐波减速器是工业机器人的关键核心部件，其可靠性的实时评估和剩余寿命预测对于提升工业机器人的工作性能和健康监管具有重要意义．作为一种复杂的高精度机械部件，其退化过程表现出明显的多阶段性特点．因此，针对谐波减速器的退化特性，提出基于Gamma过程的多阶段退化模型对谐波减速器性能退化过程进行精确描述．首先，根据谐波减速器退化趋势的变化，进行多阶段退化过程的划分；然后采用历史性能指标数据，基于最大皮尔逊相关系数准则估计模型先验分布的超参数，建立基于Gamma过程的多阶段退化模型．在此基础上，针对在役设备的实际运行特点和工程现场中性能指标数据获取困难的问题，提出采用振动特征来建立高斯过程回归模型，对性能指标值进行精准预测以实现对退化模型后验分布参数的实时更新．最后在此基础上对谐波减速器进行实时可靠性评估和剩余寿命预测．通过对谐波减速器可靠性实验数据的分析表明，所提出的方法能够实现可靠性的实时评估，并且与单一阶段退化模型相比，该方法对剩余寿命的预测精度更高．

多阶段；Gamma过程；高斯过程回归；可靠性评估；寿命预测

可靠性评估和剩余寿命预测是保证机械装备正常运维和质量监管的两大关键技术．按照数据类型，现有的可靠性和寿命预测的建模方法主要分为两类：基于失效时间数据的传统建模方法和基于性能退化数据的建模方法．而随着目前越来越多的设备呈现出高可靠性、长寿命的特点，失效数据越来越难以获得，某些复杂装备甚至会出现零失效的情况，这导致基于失效数据的退化建模陷入困境．而设备的性能退化数据可通过寿命实验直接获得，因此基于性能退化数据的建模方法逐渐成为目前的主流方法．

近年来，国内外学者对基于性能退化数据的可靠性和寿命预测建模方法展开了大量研究，主要包括失效物理模型、机器学习模型、退化量分布模型以及随机过程模型等．其中，基于失效物理的建模方法[1-2]是通过分析设备的失效机理和外部条件，然后建立失效物理模型．该方法的预测精度较高，但需要对具体设备的机理进行具体分析，因此可推广性和实际应用性较差．而基于机器学习的建模方法[3-6]在退化数据不具备规律性或是非线性的情况时，虽然模型适用性较好，但是当退化数据较少时，其精度难以保证．退化量分布模型方法[7-10]是一种基于统计学的建模方法．该方法对退化过程的波动性特点适应性较强，但是受工况环境和测量误差的随机性影响更大．

基于随机过程的可靠性建模方法考虑到了退化过程中的随机性影响，将性能指标随时间的演变看作一种随机过程，因此可以更加准确地描述设备退化过程中的随机性．常用的随机过程模型包括Gamma过程、Wiener过程以及逆高斯过程．Cheng等[11]针对退化建模中存在的先验信息获取困难的问题，提出了基于最大期望和蒙特卡洛算法的Wiener过程模型，通过轴承退化实例表明该方法能够有效提高预测精度.王书锋等[12]提出了一种基于自助法的一元Wiener过程寿命预测方法，通过对GaAs激光器的实例分析证明了方法的可行性．蔡景等[13]针对滚轮滑轨的少样本问题，提出了一种基于带漂移布朗运动的退化建模方法，实例结果证明了该方法的有效性．潘东辉[14]针对具有线性单调退化过程的设备，提出了一种基于逆高斯过程的退化建模和寿命预测方法，仿真和实例结果表明该方法能够获得较精确的预测结果．王卫国等[15]、张英波等[16]针对实际作业中的数据缺失问题，提出了基于经验最大化算法和粒子滤波算法相结合的Gamma过程退化模型，通过减速器裂纹退化数据验证了模型的有效性．Shah等[17]采用Gamma过程作为单调随机模型来模拟退化过程，实现了对剩余寿命的准确预测．

通过以上分析，目前所采用的建模方法大多都是针对单一退化过程而言的，而谐波减速器作为一种复杂的高精度机械部件，其退化过程中存在明显的非线性和多阶段性特点．如果直接采用单一阶段退化模型进行建模，会衰减掉退化过程中各拐点处的趋势性信息，使得各阶段的寿命预测精度和可靠性评估的准确度大大降低．因此，本文针对谐波减速器的多阶段性退化特点，提出了一种基于Gamma过程的多阶段退化建模方法以实现对谐波减速器性能的可靠性评估和寿命预测；其次，针对工程实际中在役设备的性能指标数据难以获取而振动数据容易获取的特点，提出建立高斯过程回归预测模型，实现了基于振动特征的性能指标值的预测，在此基础上通过该值对多阶段退化模型的后验分布参数进行实时更新，最后对谐波减速器进行实时可靠度评估和剩余寿命预测．

1 基于Gamma过程的多阶段退化建模原理

1.1 Gamma随机过程描述

Gamma过程是一个增量非负且独立同分布的连续时间随机过程，该随机过程具有以下特性．

当设备的退化过程满足以上3点时，可采用Gamma过程进行退化建模．

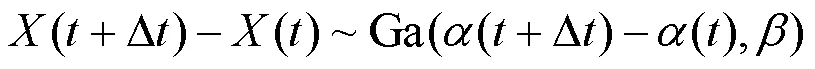
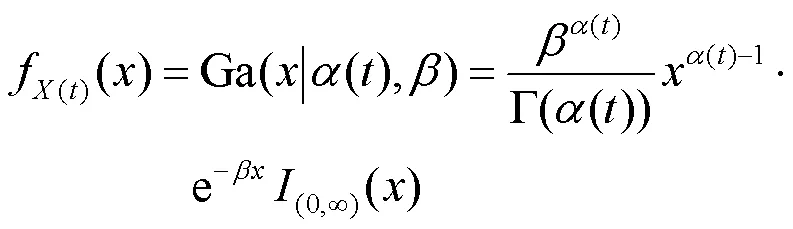
1.2 基于Gamma过程的多阶段退化建模

对于复杂机械装备来讲，其整个寿命期的退化过程呈现多阶段特性，换言之，在退化初期、中期及后期，设备的性能指标退化速率会发生明显的改变．采用单一的Gamma过程无法实现对其退化性能的准确描述，因此本文提出基于Gamma过程的多阶段退化过程模型．

对于复杂的谐波减速器而言，认为其退化过程满足以下假设．

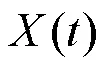
基于以上假设，建立多阶段退化过程模型，即

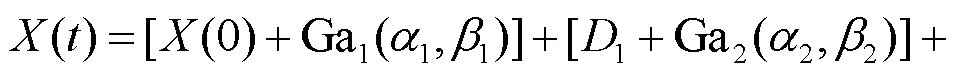
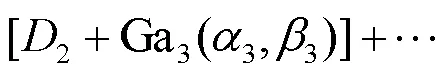
假设为设备的寿命，对于单调递增的退化过程，时刻的可靠度函数定义为

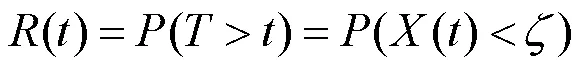
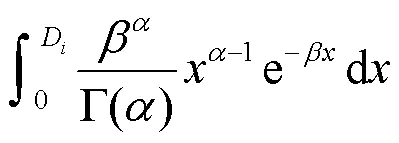
2 基于多阶段退化模型的实时可靠性评估与剩余寿命预测流程

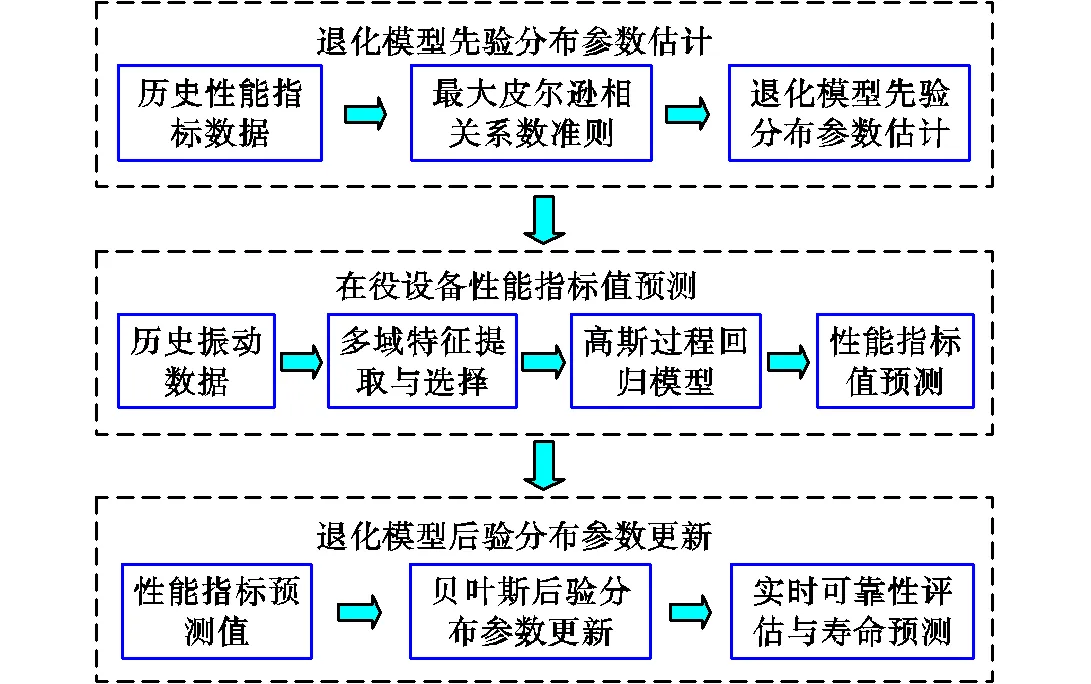
图1 基于多阶段退化过程的可靠性评估与剩余寿命预测方法流程

可靠性评估与剩余寿命预测实现步骤如下．

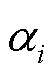
步骤2对历史振动数据进行滤波处理，并进行特征提取．以历史振动特征为训练集输入，历史性能指标数据为训练集标签，建立基于高斯过程的回归预测模型，实现从振动特征到性能指标值的预测建模．

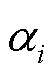
各步骤具体参数设定见第2.1节至第2.3节．

2.1 退化模型先验分布参数估计

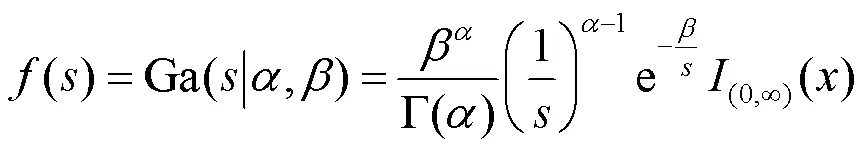
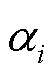
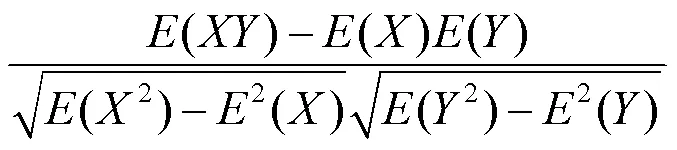
2.2 基于高斯过程回归的在役设备性能指标值预测

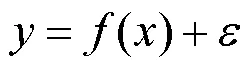
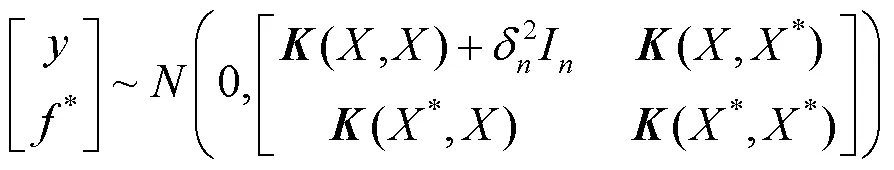
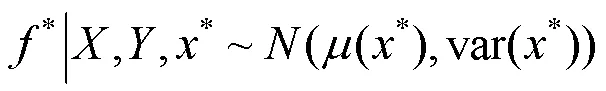
2.3 退化模型后验分布参数更新

的后验概率密度函数为

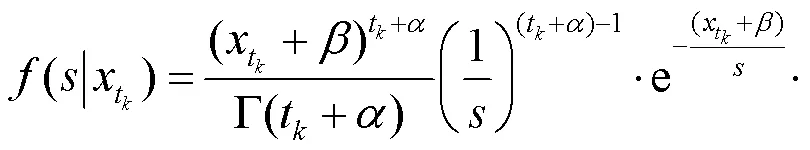
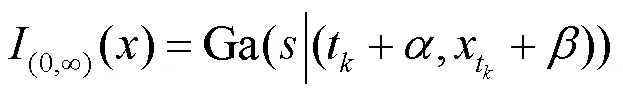
则的后验期望估计为

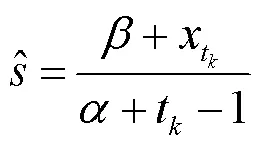
基于式(13)可计算出参数更新后的各阶段实时可靠度函数曲线，并在此基础上可计算出任一可靠度下的可靠寿命和平均寿命，实现对剩余寿命的预测．

3 实验验证

3.1 退化实验及数据

本文搭建了谐波减速器实验台进行寿命实验，以采集历史退化数据，包括同步采集的振动数据和回转误差数据．其中回转误差数据作为谐波减速器的性能指标，表征谐波减速器的性能退化失效，用以建立多阶段退化模型．振动数据用来建立高斯过程的回归预测模型，实现对性能指标值的预测，进而通过该值对多阶段退化模型进行后验参数更新以实现实时可靠度的评估和寿命预测．

实验平台由驱动电机、皮带、谐波减速器、负载砝码、支撑板和连接板组成，如图2所示．其中谐波减速器采用礼帽型谐波减速器，具体参数如表1所示.

图2 谐波减速器实验平台

表1 谐波减速器参数

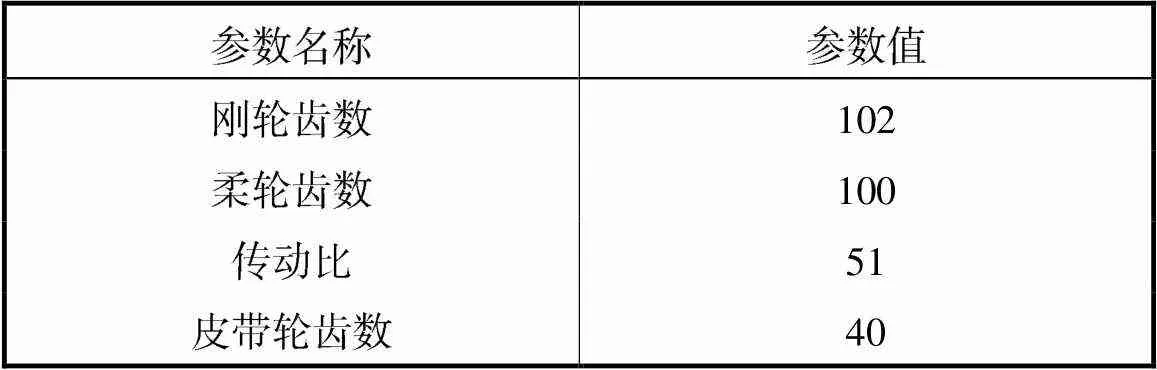
Tab.1 Parameters of the harmonic reducer

为使得谐波减速器实验工况更接近于实际作业状态，本实验设定负载端转矩为30N·m，电机转速按照0—2000r/min—0—-2000r/min—0运转，使得谐波减速器带动负载砝码循环往复运动，正反转一周期历时3s．

本实验采用杠杆式千分表测量回转误差值，测量精度为角秒级别，根据现场工程师所言，谐波减速器工作精度较高，当回转误差达到100角秒以上时，可认为精度已失效，不可再用．因此本实验回转误差的失效阈值定为105角秒．采用三向振动传感器测量振动数据，测量精度为，传感器位于支撑板上方，采样频率为5120Hz．实验从回转误差50角秒开始测量，共持续12周，每周五同一时间对其回转误差及振动进行测量，采集时间为180s，其余时间谐波减速器连续运行，每天工作时长24h．每次采集的振动数据长度为921600，回转误差数据取平均值作为该周当前回转误差值，回转误差曲线如图3所示．

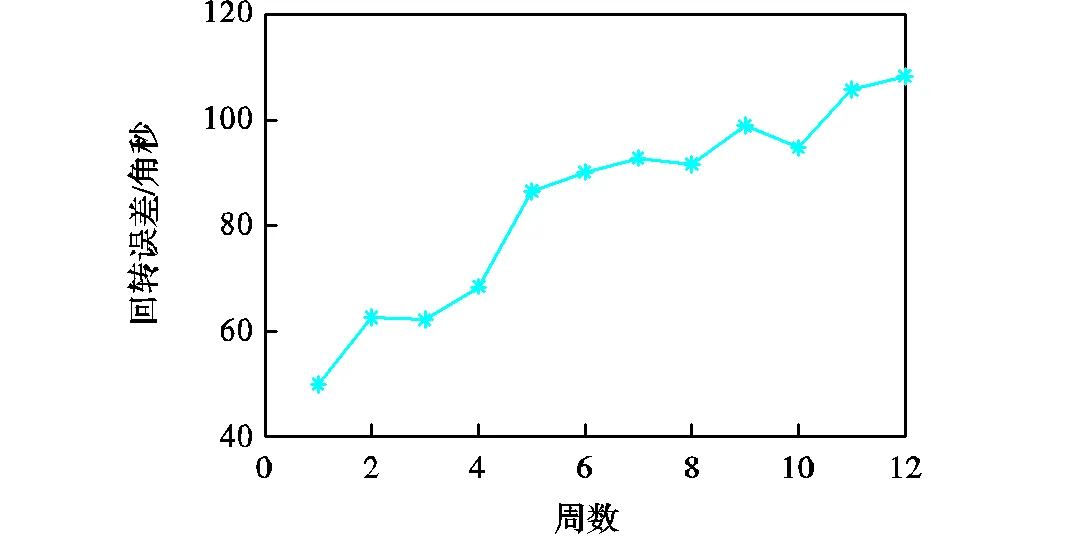
图3 回转误差

3.2 基于Gamma过程的多阶段退化建模

3.2.1 退化过程多阶段划分

由第3.1节可知本实验为期12周，共采集回转误差数据12个，数据间隔为7d．在寿命预测时时间间隔太长，难以用于实际工程当中，故本文对谐波减速器回转误差数据进行3次样条插值拟合，设定12个观测值为3次样条算法的输入，84作为待插值个数，通过计算将回转误差曲线划分为84个观测值，相邻观测点间隔为24h，如图4所示．其中红色为12个实际采集值，蓝色为84个插值后回转误差值．

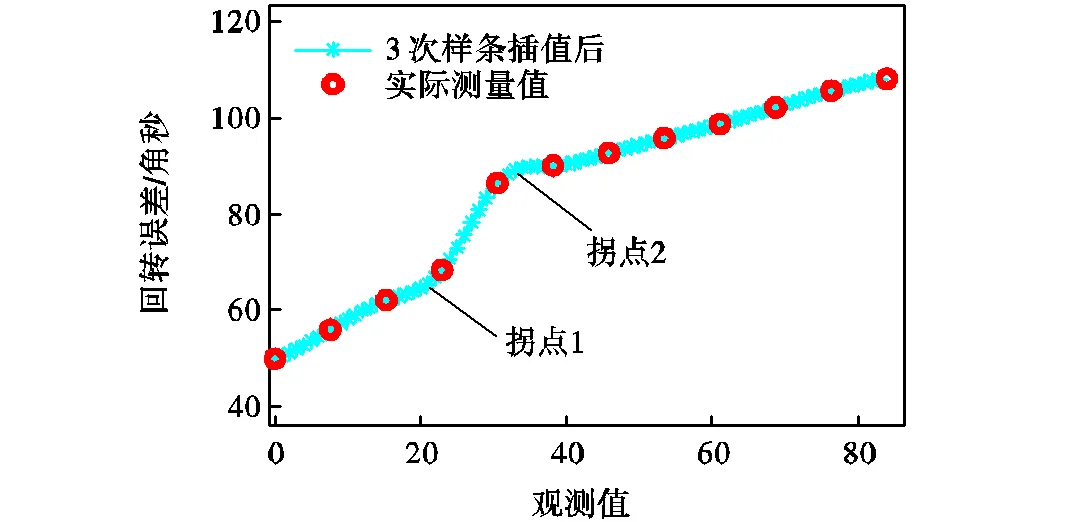
图4 谐波减速器回转误差观测值

由图4可以看出，退化曲线存在两个明显的拐点，分别为第22和第35观测值位置．在两拐点处，谐波减速器的退化趋势发生了明显的改变，退化率在拐点1处开始增大，在拐点2处又开始减小．通过分析可以看出谐波减速器的退化过程确实存在多阶段特性，下面对其进行多阶段划分．

第22和第35观测值处回转误差分别为66.89角秒和89.67角秒，因此以65角秒和90角秒为界，将退化过程人为划分为3个阶段．并设定最终失效阈值为105角秒，可知在第76个观测值(回转误差为105.2角秒)时，设备首次达到失效阈值，认定设备已退化失效．

谐波减速器退化过程阶段划分如表2、图5所示.

表2 退化过程多阶段划分

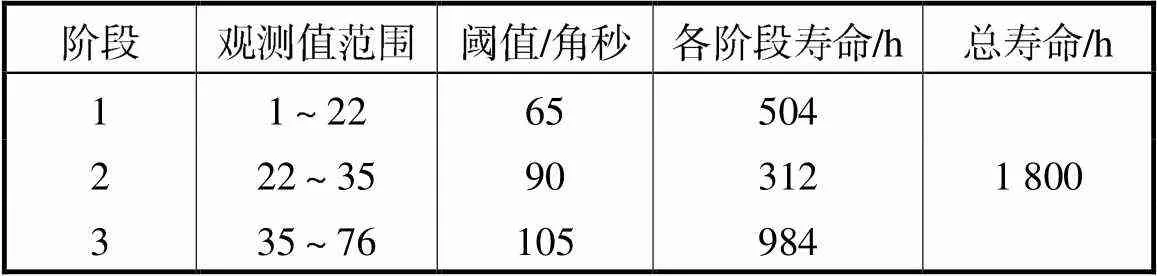
Tab.2 Multistage division of the degradation process

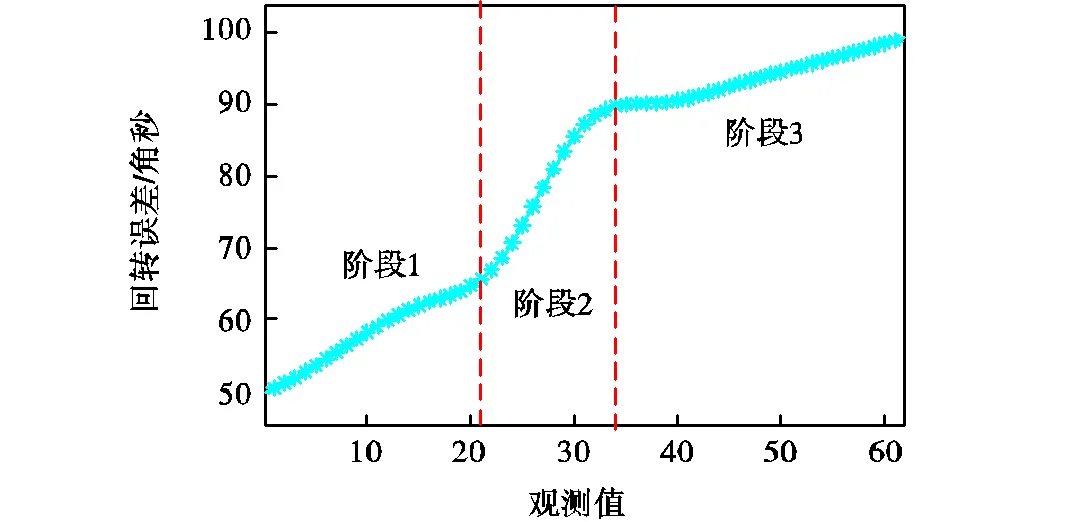
图5 退化过程多阶段划分

3.2.2 退化过程仿真

为提高模型先验分布参数估计的准确性，基于蒙特卡洛方法对退化过程进行仿真并生成仿真退化数据．真实退化数据与仿真退化数据共同作为历史性能指标数据，用于可靠性建模．

表3 各阶段参数

Tab.3 Parameters of each stage

采用估计后的各阶段参数值，基于蒙特卡洛方法进行随机抽样并生成仿真退化曲线．各阶段退化轨迹如图6所示．

3.2.3 多阶段退化模型先验分布参数估计

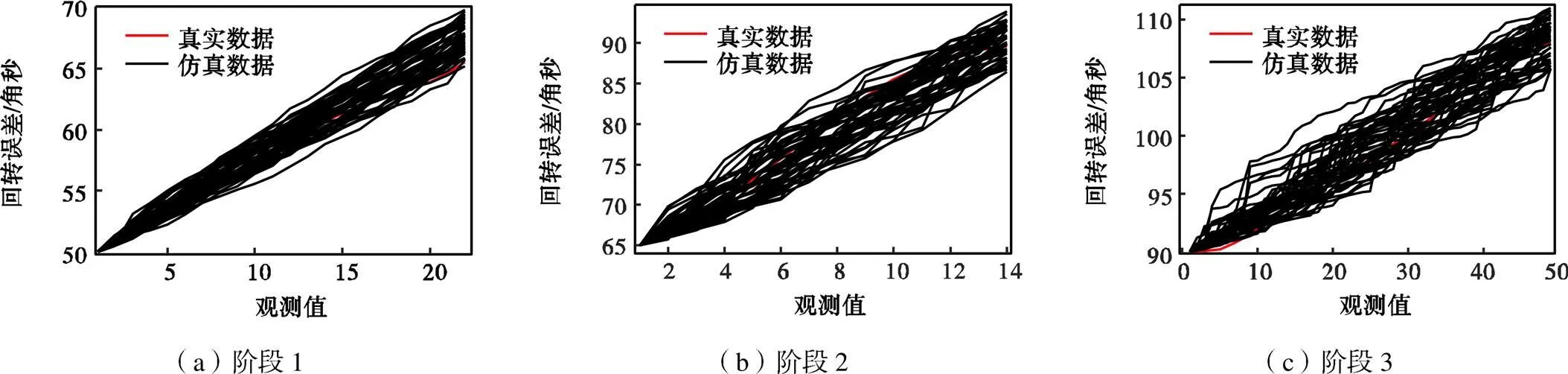
图6 各阶段退化轨迹

表4 各阶段相关系数

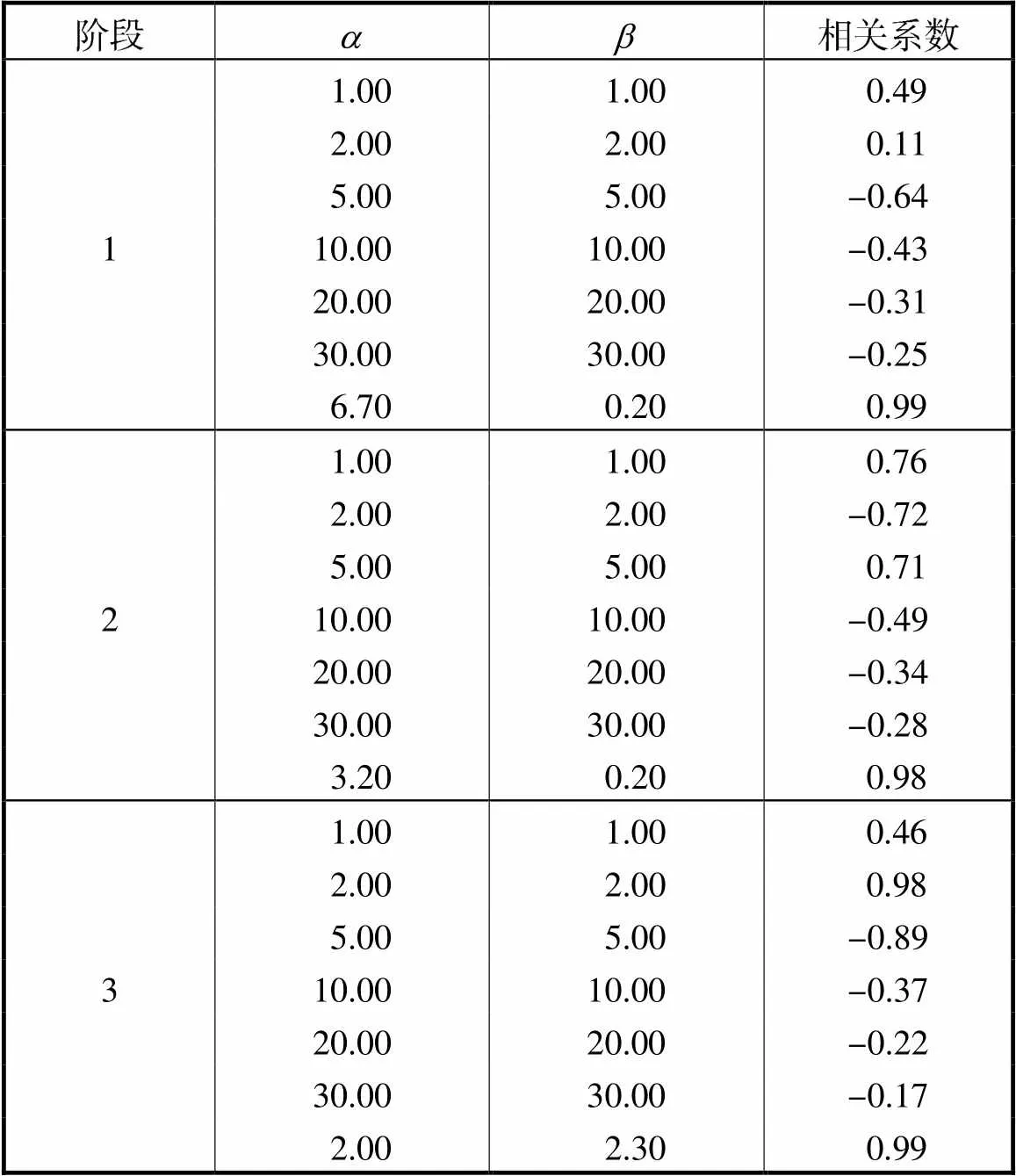
Tab.4 Correlation coefficients of each stage

表5 各阶段最大相关系数

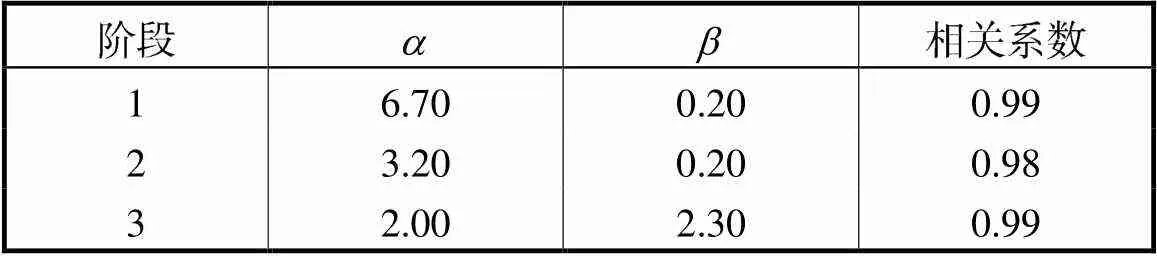
Tab.5 Maximum correlation coefficients of each stage

3.3 基于高斯过程回归的性能指标值预测

由于在实际作业中谐波减速器的回转误差无法采集，而振动数据容易采集，因此本节建立谐波减速器的振动数据和回转误差之间的预测模型，通过该预测模型和实时采集的振动数据来预测当前状态下的回转误差，进而对第3.2节的多阶段退化模型进行更新，最后实现对可靠性的实时评估和寿命预测．

第3.1节中工况为0—2000r/min—0—-2000r/min—0的变转速工况，因此根据表1谐波减速器的参数计算最大转速2000r/min时的特征频率，如表6所示．

表6 特征频率

Tab.6 Characteristic frequencies

由表6可知，2000r/min转速下谐波减速器的柔轮特征频率最大，为66.67Hz，因此其他转速下谐波减速器的各个特征频率均小于66.67Hz，又因为皮带轮啮合频率为1333.33Hz，故对12周振动数据进行低通滤波处理，频率截止上限设为500Hz，以涵盖谐波减速器所有特征频率，并滤掉皮带轮的啮合频率．

滤波后各周数据总长度仍为921600，截取各周样本长度为30000作为一样本，共提取30个样本，12周共计样本总数为360个．

对所有样本进行时域、频域及时频域特征提取，共提取26种特征，如表7所示．部分特征的12周特征趋势如图7所示．

表7 振动特征

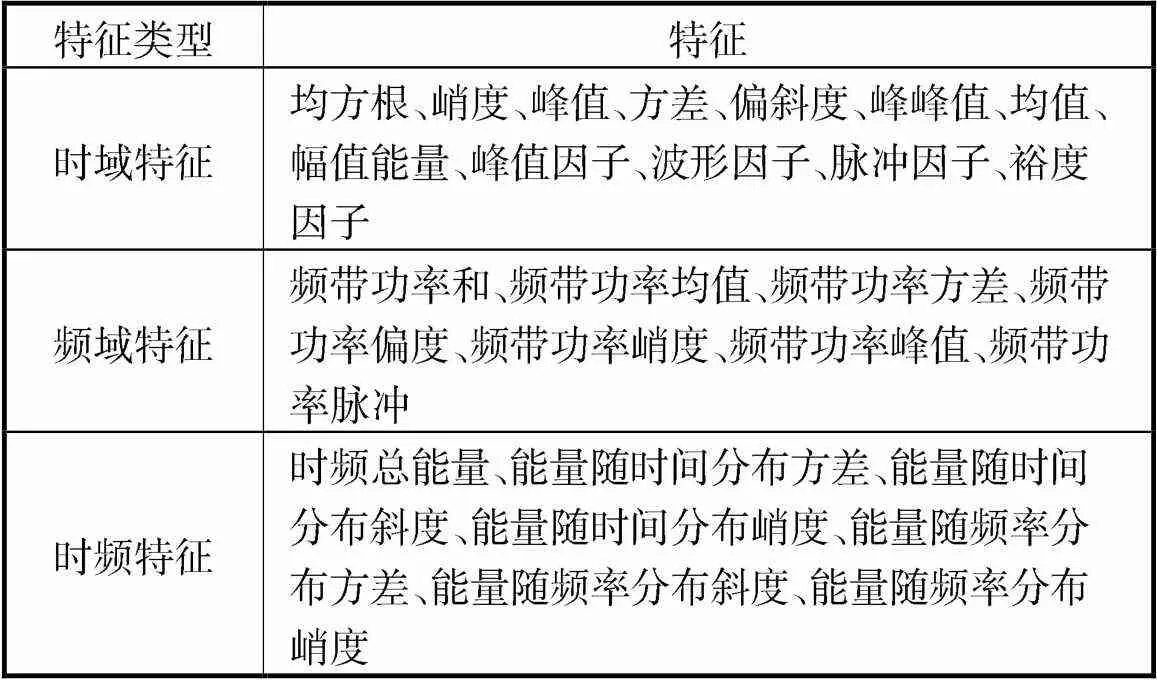
Tab.7 Characteristics of vibration

从图7可看出，有些特征的趋势呈现单调趋势，而某些特征则无规律．然而随着谐波减速器不断退化，回转误差的变化是单调的，因此应选择单调趋势的特征进行预测建模．故本文根据特征趋势性，最终选择单调性较好的有效值、方差、幅值能量、频带功率和、频带功率均值及时频总能量6种特征组成特征向量进行预测建模，共计特征样本360×6个．

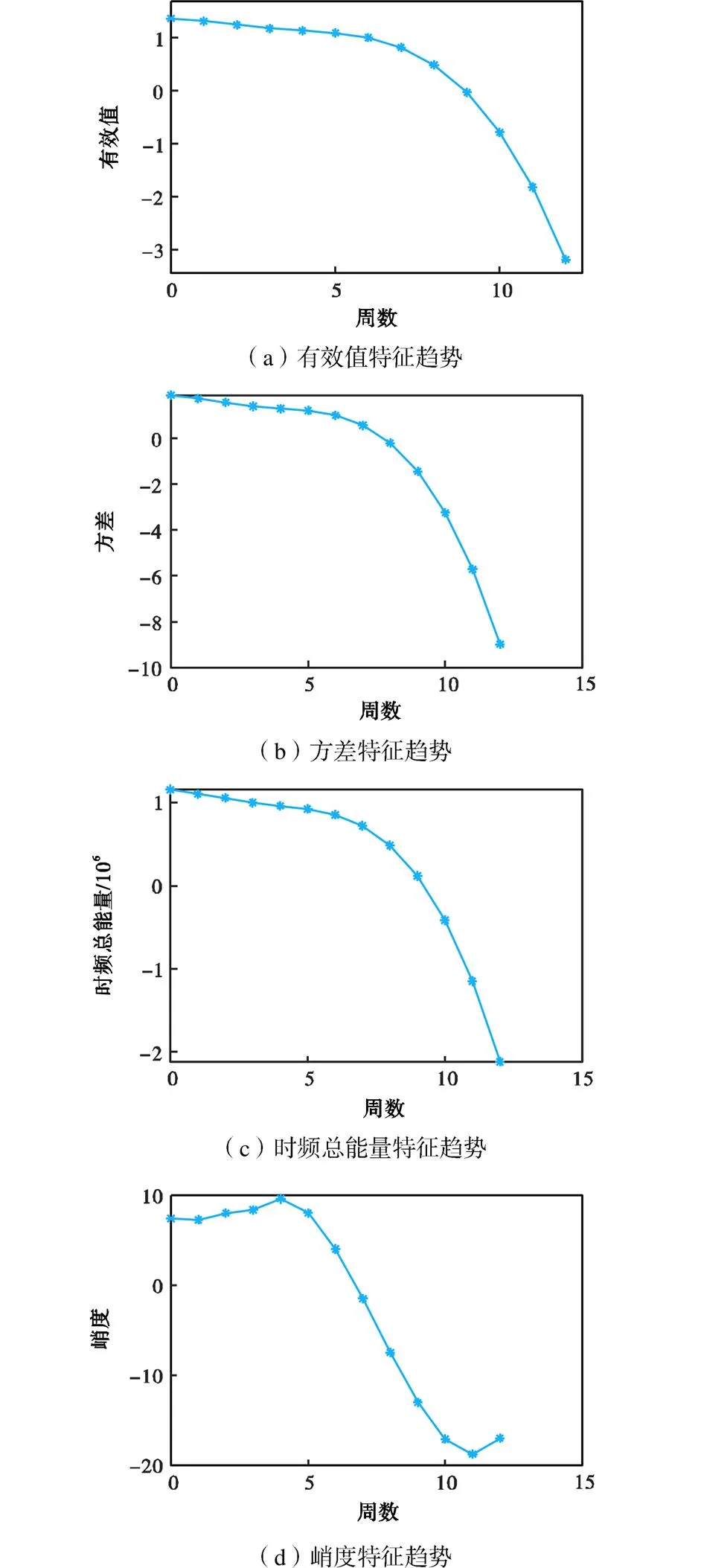
图7 部分振动特征趋势

随机选取每周数据的20个样本特征集作为训练集输入，剩余10个样本特征集作为测试集输入，采用对应数量的回转误差数据作为训练集标签(240×1)和测试集标签(120×1)．其中测试集标签不参与预测建模过程，只用于评估模型的预测精度．由此建立高斯过程回归预测模型进行预测，图8为高斯过程回归模型预测结果．

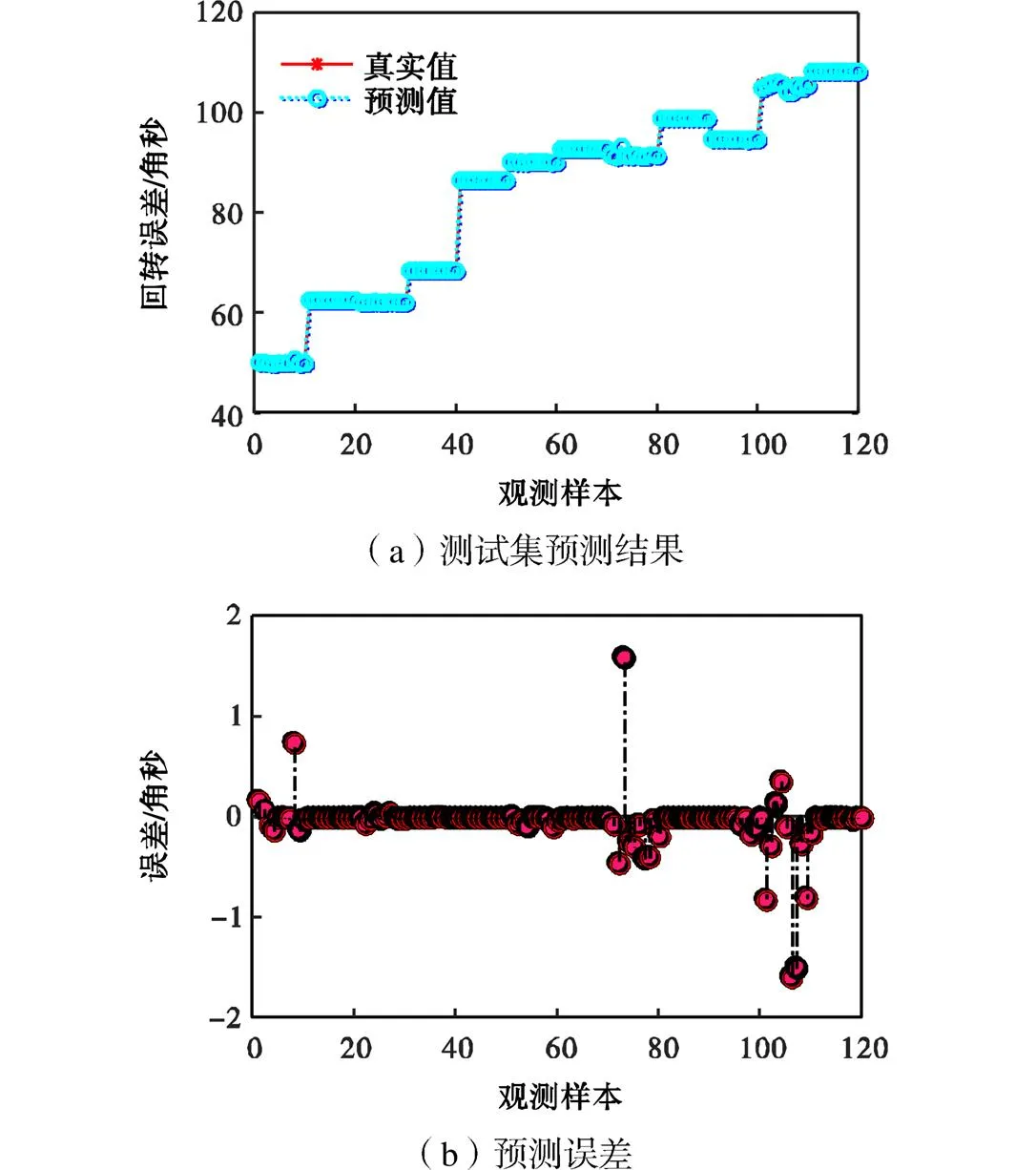
图8 高斯过程回归模型预测结果

从图8中可以看出高斯过程模型的预测误差很小，预测效果较好．

为比较高斯过程回归模型与其他模型的预测精度，本文基于相同特征集，采用支持向量机回归模型和神经网络回归模型进行回归预测，模型参数如表8所示．同时为了更直观地比较预测精度，采用均方根

表8 模型参数

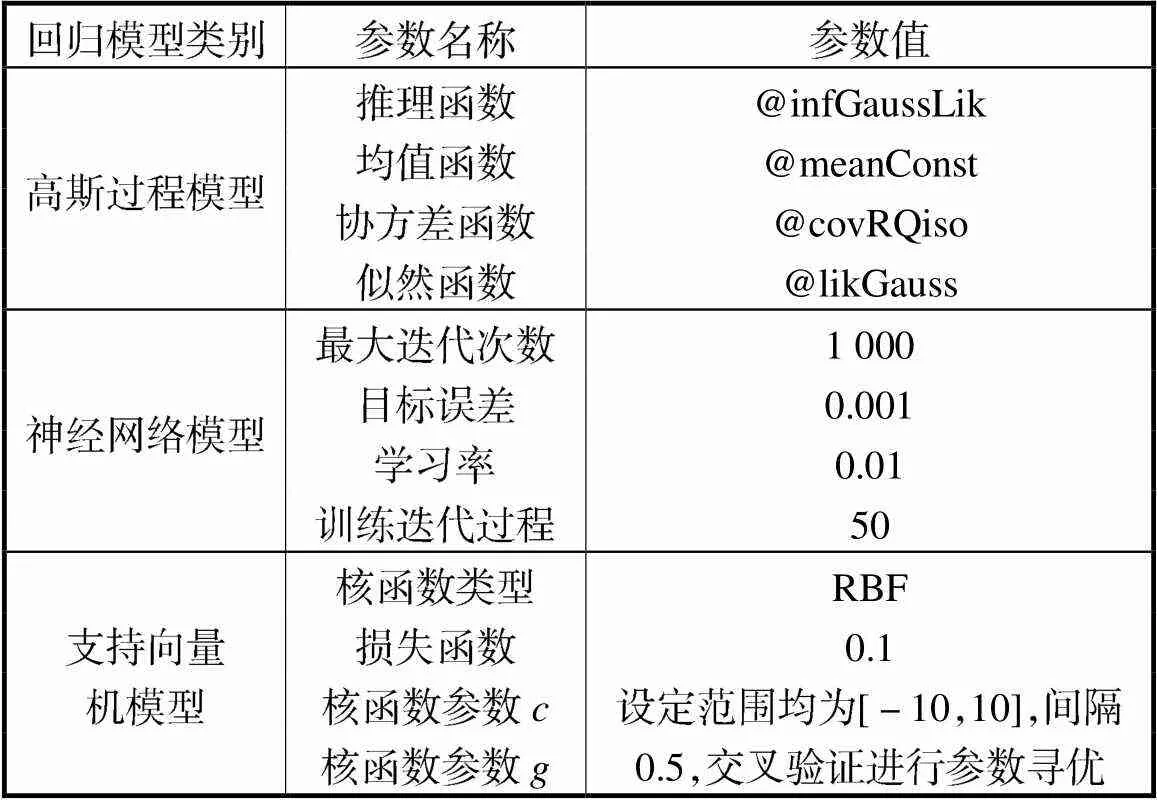
Tab.8 Model parameters

误差(RMSE)、相对误差(RE)、拟合优度(2)、准确因子(f)以及运行时间()5种评判指标进行评估，计算公式如下．

1) 均方根误差(RMSE)

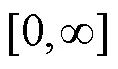
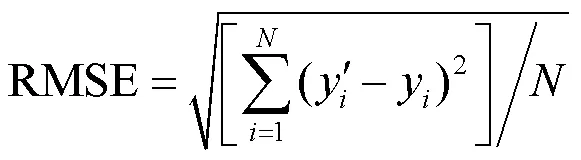
2) 相对误差(RE)

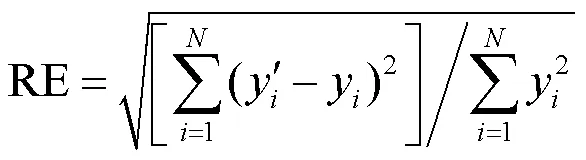
3) 拟合优度(2)

2又称为决定系数．范围为[0，1]，越接近1代表模型的性能越好，越接近0代表性能越差，经验表明决定系数大于0.4则代表拟合效果较好．表达式为

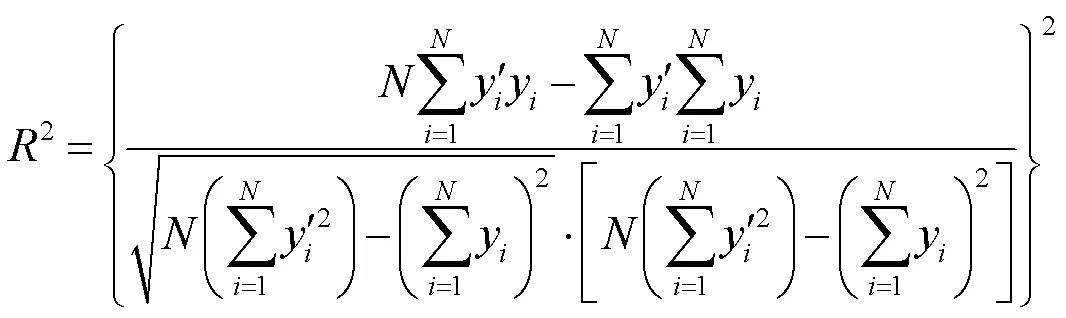
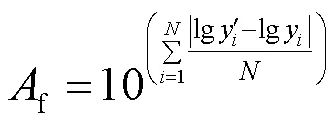
预测结果如图9、图10及表9所示．

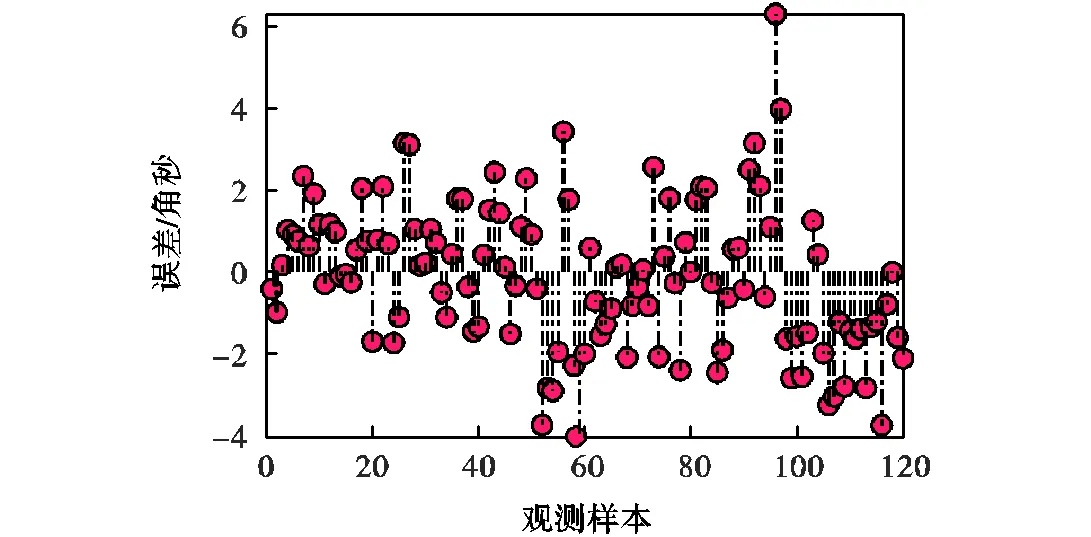
图10 神经网络回归模型预测结果

表9 模型预测精度判别

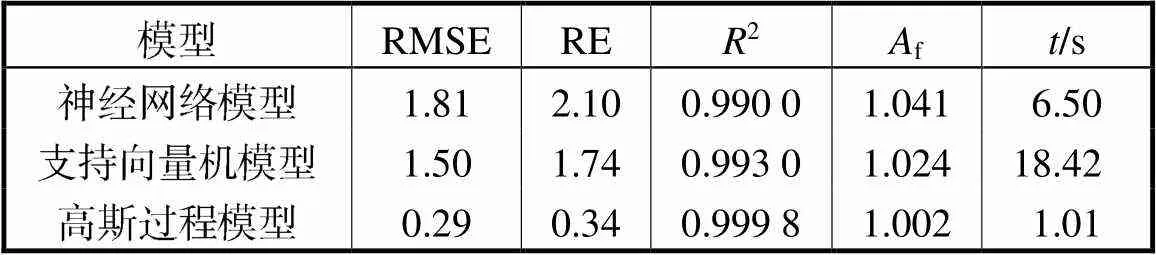
Tab.9 Discrimination of the models’ prediction accuracy

对比图8～图10可以看出高斯过程回归模型的预测精度要高于支持向量机回归和神经网络回归模型．从表9也可以看出高斯过程回归模型的均方根误差和相对误差要远小于神经网络回归模型和支持向量机回归模型，拟合优度和精确因子也更接近于1，同时建模所耗时间最短．各项指标均表明高斯过程回归模型的预测效果最好，能够实现对回转误差值的精确预测．

3.4 实时可靠度评估与剩余寿命预测

将谐波减速器当前时刻下的实测振动数据按照第3.3节的预处理方式进行滤波及6种特征的提取，将该特征向量作为回归预测模型输入，预测出当前时刻下的回转误差值，并基于此值对第3.2节的退化模型进行后验分布参数进行更新，通过式(13)可计算得出当前时刻下的谐波减速器的实时可靠度曲线，如图11所示．

图11中18表示通过此时的振动特征预测出当前状态下的回转误差值，并以此值进行参数更新后的阶段1的谐波减速器实时可靠度曲线．其他曲线依此类推．

本文设定可靠度为0.01时设备已失效，此时的寿命即为谐波减速器总体可靠寿命．例如图中18曲线，当可靠度为0.01时，总体可靠寿命为466.5h，此时谐波减速器已工作408.0h，则可得出剩余寿命的预测值为58.5h，其他曲线依此类推．

为使预测结果更为直观，本文绘制阶段2的剩余寿命真实值与预测值进行对比说明，如图12所示．

从图12可看出，随着退化量的增加，谐波减速器的实时可靠性和剩余寿命的预测准确度逐渐提高，不断接近于真实值．

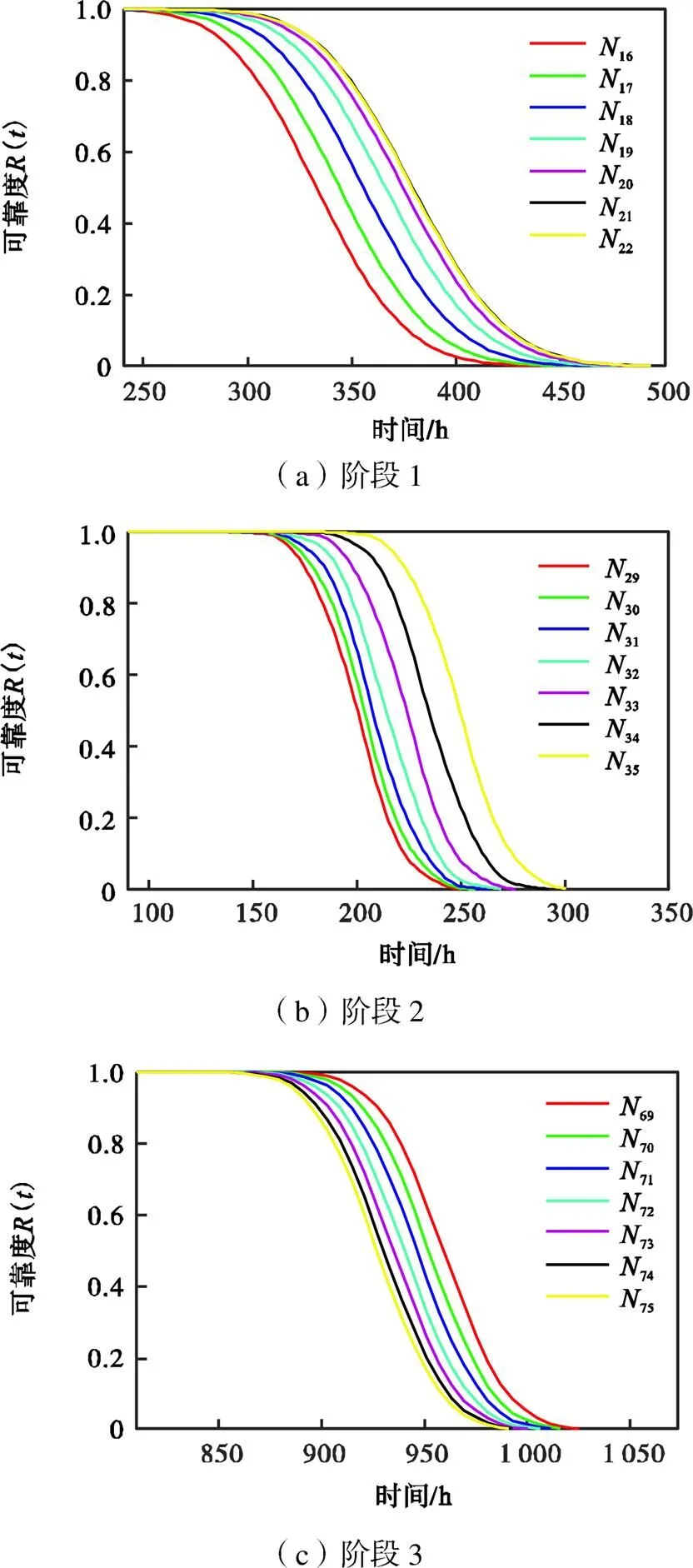
图11 多阶段退化过程实时可靠度

为比较多阶段退化模型和单一阶段退化模型的预测效果，本文再次采用单一阶段的Gamma过程进行建模，并对两方法的寿命预测结果进行比较，结果如表10所示．

从表10中可以看出，在阶段1和阶段3中，多阶段退化模型的预测结果比单一阶段退化模型更接近于真实值，且随着退化数据的增多，多阶段退化模型的预测效果逐渐提高，误差较小；在阶段2中，多阶段退化模型的预测精度要远高于单一阶段预测模型，且随着退化量的增加，多阶段模型的预测效果逐渐接近真实值，误差极小．阶段2下两种方法的谐波减速器的剩余寿命预测结果如图13所示．

阶段2为谐波减速器的退化过程发生明显曲率变化的阶段．由图13可见，此时多阶段退化模型的寿命预测值与真实值极为接近，而单一阶段模型的预测值与真实值相差较大．因此多阶段退化模型更为适用，预测精度更高．

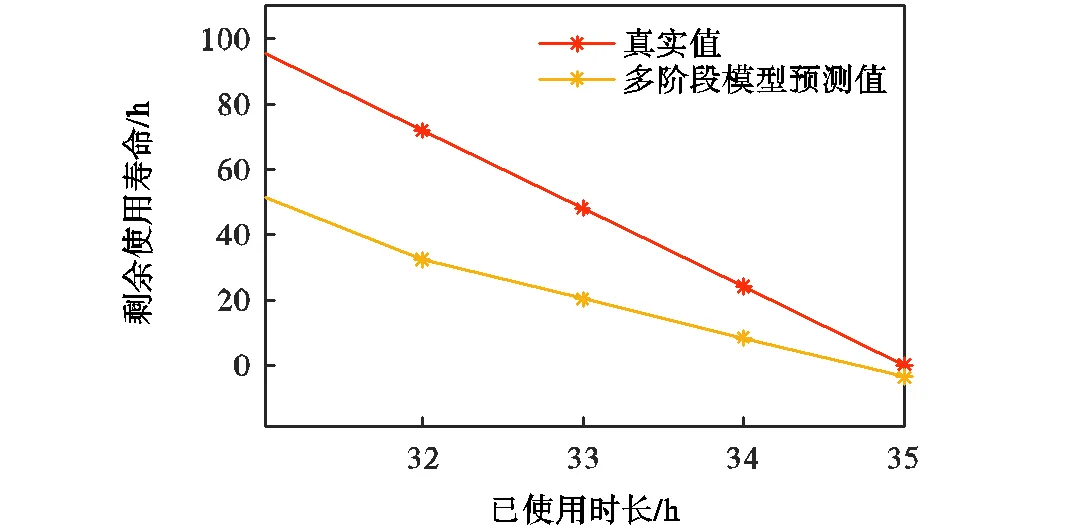
图12 阶段2剩余寿命预测

表10 剩余寿命预测

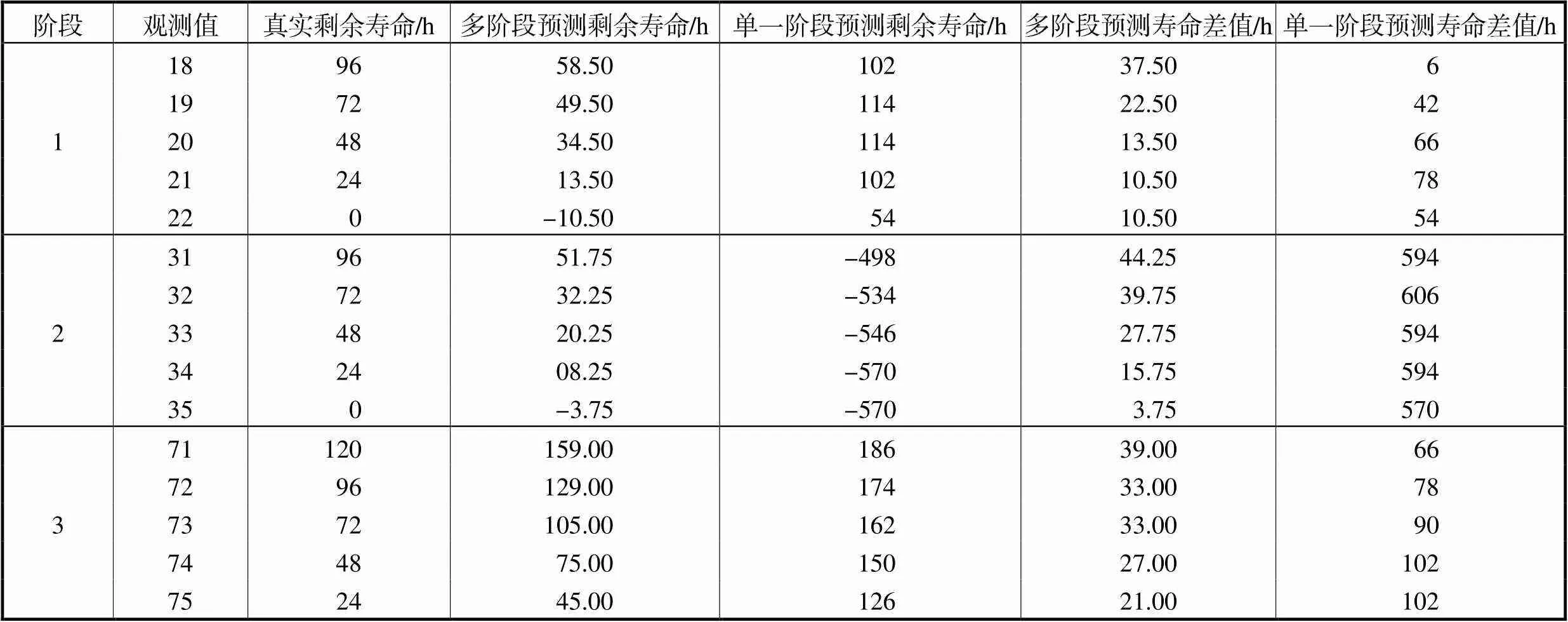
Tab.10 Remaining life predictions

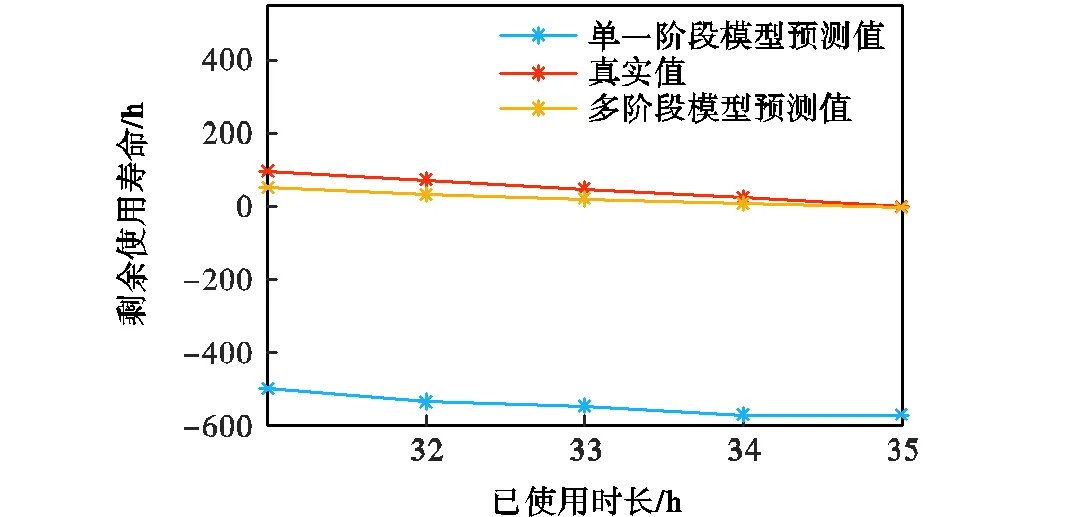
图13 剩余寿命预测

4 结 语

针对谐波减速器多阶段退化过程特点，本文所提出的多阶段退化过程模型能够对其进行精确描述，并且对实时可靠性和剩余寿命的预测精度比单一阶段退化过程模型更加准确，预测效果更为显著．同时，本文所建立的高斯过程回归预测模型，实现了对谐波减速器性能指标值的精准预测，为后验分布参数的更新提供了精确保证，进一步提高了实时可靠性评估和剩余寿命预测的准确度．

［1］ 袁 容. 基于性能退化分析的可靠性方法研究[D]. 成都：电子科技大学，2015.

Yuan Rong. Research on Reliability Method Based on Performance Degradation Analysis[D]. Chengdu：University of Electronic Science and Technology of China，2015 (in Chinese).

［2］ Meeker W Q，Escobar L A. Statistical Methods for Reliability Data[M]. New York：Wiley，1998.

［3］ 郭 琦. 基于性能退化数据的可靠性评估方法研究[D]. 广州：华南理工大学，2015.

Guo Qi. Research on Reliability Evaluation Method Based on Performance Degradation Data[D]. Guangzhou：South China University of Technology，2015 (in Chinese).

［4］ Tao T，Zio E，Zhao W. A novel support vector regression method for online reliability prediction under multi-state varying operating conditions[J]. Reliability Engineering and System Safety，2018，177：35-49.

［5］ 王国锋，董 毅，杨 凯，等. 基于深度学习与粒子滤波的刀具寿命预测[J]. 天津大学学报(自然科学与工程技术版)，2019，52(11)：1109-1116.

Wang Guofeng，Dong Yi，Yang Kai，et al. Tool life prediction based on deep learning and particle filtering[J]. Journal of Tianjin University(Science and Technology)，2019，52(11)：1109-1116(in Chinese).

［6］ 周亚同，陈子一，马尽文. 从高斯过程到高斯过程混合模型：研究与展望[J]. 信号处理，2016，32(8)：960-972.

Zhou Yatong，Chen Ziyi，Ma Jinwen. From Gaussian processes to the mixture model of Gaussian processes：A survey[J]. Journal of Signal Processing，2016，32 (8)：960-972 (in Chinese).

［7］ 邓爱民，陈 循，张春华，等. 基于性能退化数据的可靠性评估[J]. 宇航学报，2006，27(3)：546-552.

Deng Aimin，Chen Xun，Zhang Chunhua，et al. Reliability assessment based on performance degradation data[J]. Journal of Astronautics，2006，27(3)：546-552 (in Chinese).

［8］ 官 浩，王安宇，吴鸿涛. 谐波减速器寿命分布可靠性模型[J]. 机械设计与研究，2016，32(6)：46-48.

Guan Hao，Wang Anyu，Wu Hongtao. Study of life distribution reliability model for harmonic driver[J]. Mechanical Design and Research，2016，32(6)：46-48 (in Chinese).

［9］ Mohamad G，Satish C. An experimental investigation of cutting tool reliability and its prediction using Weibull and Gamma models：A comparative assessment[J]. Materials Today，2020，24(2)：1478-1487.

［10］ Yemeserach M，Haneen A，Arif S. Life cycle prediction of sealed Lead acid batteries based on a Weibull model[J]. Journal of Energy Storage，2018，18：467-475.

［11］ Cheng Yiwei，Zhu Haiping，Hu Kui，et al. Reliability prediction of machinery with multiple degradation characteristics using double-Wiener process and Monte Carlo algorithm[J]. Mechanical Systems and Signal Processing，2019，134：1-23.

［12］ 王书锋，王友仁，姜媛媛. Wiener过程性能退化电子产品的剩余寿命预测方法[J]. 电子测量技术，2014，37(5)：17-20，41.

Wang Shufeng，Wang Youren，Jiang Yuanyuan. Residual life prediction method of electronic products with Wiener process degradation[J]. Electronic Measurement Technology，2014，37(5)：17-20，41(in Chinese).

［13］ 蔡 景，任淑红，陆晓华. 基于带漂移布朗运动的滚轮滑轨可靠性预测方法研究[J]. 中国机械工程，2012，23(12)：1408-1412.

Cai Jing，Ren Shuhong，Lu Xiaohua. Research on reliability prediction for roller-slide based on Brownian motion with drift[J]. China Mechanical Engineering，2012，23(12)：1408-1412(in Chinese).

［14］ 潘东辉. 基于退化数据的产品可靠性建模与剩余寿命预测方法研究[D]. 武汉：华中科技大学，2014.

Pan Donghui. Research on Product Reliability Modeling and Residual Life Prediction Based on Degradation Data [D]. Wuhan：Huazhong University of Science and Technology，2014 (in Chinese).

［15］ 王卫国，孙磊. 基于Gamma过程和EM-PF参数估计的剩余寿命预测方法研究[J]. 军械工程学院学报，2015，27(2)：1-7.

Wang Weiguo，Sun Lei. Residual useful life prediction research based on Gamma process and EM-PF parameter estimation algorithm[J]. Journal of Ordnance Engineer-ing College，2015，27(2)：1-7(in Chinese).

［16］ 张英波，贾云献，冯添乐，等. 基于Gamma退化过程的直升机主减速器行星架剩余寿命预测模型[J]. 振动与冲击，2012，31(14)：47-51.

Zhang Yingbo，Jia Yunxian，Feng Tianle，et al. Remaining useful life prediction model of planetary carrier in helicopter main gear-box based on Gamma degradation process[J]. Journal of Vibration and Shock，2012，31 (14)：47-51 (in Chinese).

［17］ Shah L，Om P Y. Predicting remaining lifetime using the monotonic Gamma process and Bayesian inference for multi-stress conditions[J]. Procedia Manufacturing，2019，38：1260-1267.

Real-Time Reliability Evaluation and Life Prediction of Harmonic Reducer Based on Multistage Degradation Modeling

Wang Guofeng1，Cao Zenghuan1，Feng Haisheng2，Wang Junqi2，Hu Mantang1

(1. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China；2. Effort Intelligent Equipment Co.，Ltd.，Wuhu 241007，China)

A harmonic reducer is a key component in an industrial robot，and its real-time reliability evaluation and residual life prediction are important for improving the working performance and health supervision of the industrial robot. As a complex and high-precision mechanical component，its degradation process shows an obvious multistage characteristic. Therefore，considering the degradation characteristic of the harmonic reducer，this study proposes a multistage degradation model based on a Gamma process to accurately describe the performance degradation process of the harmonic reducer.First，the multistage degradation process is divided according to the change of the degradation trend of the harmonic reducer. Using the historical performance index data，the super parameters of the prior distribution of the model are then estimated based on the maximum Pearson correlation coefficient criterion to establish a multistage degradation model based on a Gamma process. In addition，aiming at the actual operating characteristics of the equipment in service and the difficulty in obtaining the performance index data in the engineering site，a Gaussian process regression prediction method based on vibration characteristics is proposed to predict the performance index value. On this basis，the posterior distribution parameters are updated in real-time. Finally，the real-time reliability evaluation and the residual life prediction are carried out. The analysis of the reliability test data of the harmonic reducer shows that the proposed method can evaluate the real-time reliability of the equipment. Compared with the single-process model，this method has higher accuracy in residual life prediction.

multistage；Gamma process；Gaussian process regression；reliability assessment；life prediction

10.11784/tdxbz202008025

TH17

A

0493-2137(2022)02-0122-11

2020-08-12；

2020-12-28.

王国锋（1975—  ），男，博士，教授.Email：m_bigm@tju.edu.cn

王国锋，gfwangmail@tju.edu.cn.

国家重点研发计划资助项目(2019YFB1704802-2，2019YFA0706702)；国家自然科学基金资助项目(52075365，51675369)；国防基础科研计划资助项目(JCKY2018205C002)；天津市自然科学基金资助项目(17JCZDJC40100)；天津市宇航智能装备技术企业重点实验室开放课题资助项目(TJYHZN2019KT003)．

the National Key Research and Development Program of China(No. 2019YFB1704802-2，No. 2019YFA0706702)，the National Natural Science Foundation of China(No. 52075365，No. 51675369)，the National Defense Basic Research Program Funding(No. JCKY2018205C002)，the Natural Science Foundation of Tianjin，China(No. 17JCZDJC40100)，the Key Laboratory Open Project of Tianjin Aerospace Intelligent Equipment Technology Enterprise(No. TJYHZN2019KT003)．

(责任编辑：王晓燕)