桌面型607 机械臂工作空间及奇异位形分析

张倩玉，张宇，陈昊然，段昊宇翔

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

近年来，机器人技术在许多领域发挥着重要作用，对它的研究也越来越深入。自从机构被发明就不可避免地存在机构的奇异问题[1]。奇异位形是除了正常工作位形外的一种特殊位形，机械臂发生的奇异位形主要分为边界奇异位形与内部奇异位形2 种[2]，它对于机械臂完成基本操作和特定任务起着重要影响。当机械臂发生奇异位形时，会对机构运动产生不利影响，如自由度变少而导致机械手无法实现某些特定运动，灵活性变差致使机构锁死等问题。当然，奇异位形也有益处，比如利用极限位置制作一些自锁机构等。因此，不管是从有利还是不利角度来说，对机械臂的奇异性问题展开研究都是非常必要的。

许多学者针对机械臂奇异性问题开展了深入的研究。舒晓春[3]利用雅可比矩阵分析了某工业机器人奇异位形发生的原因，提出了在实际工作过程中解决奇异位形的常用办法；于常娟等[4]针对不同形式驱动的并联机构,建立了雅可比矩阵，并在ADAMS 中验证所求雅可比矩阵；蔡玉强[5]等利用微分变化法求得三自由度工业拾取机械手的雅可比矩阵,并验证了机械手建立的正确性；张新[6]等用矢量积法解得该机器人机械臂的雅可比矩阵，对奇异位形和工作空间展开研究；李宪华[7]等建立了6R 机械臂的模型，得到了正运动学方程，并基于连杆速度法建立雅可比矩阵，得出该机械臂奇异位形的所有情况；李丽[8]等针对广数RB20 机械臂，运用螺旋定理求出该雅可比矩阵，并对它进行了奇异位形分析；刘青松[9]等针对轮式移动抓取机械手，利用旋量法和随机取点法解出相应的雅可比矩阵，得出奇异位形并相互印证，最后利用MATLAB 模拟求解出的奇异位形。

本文以桌面型607 串联机械臂为研究对象，首先采用标准的D-H参数法求出正运动学方程的解，并对其验证；然后，利用MATLAB 分析该工作空间；最后，利用通用的微分变换法得到其雅可比矩阵，并对其进行奇异位形研究，为机械臂避免奇异位形算法的研究提供理论依据。

1 机器人机械臂坐标系建立

桌面型607 机械臂运动范围广、运动速度快、再定位精度高，适合高速、高完成度的分拣、抓放料等工作。此机械臂是由6 个旋转副组成，根据标准的D-H 参数法，构建连杆坐标系。图1 为桌面型607 机械臂本体结构，图2 为机器臂连杆坐标系。按照桌面型607 机械臂和它对应的连杆坐标系，列出此机械臂对应的D-H 参数如表1 所示。其中：d1=179 mm，a2=340 mm，a3=53 mm，d4=300 mm。

图1 机械臂本体结构Fig.1 Robotic arm body structure

图2 连杆坐标系Fig.2 Linkage coordinate system

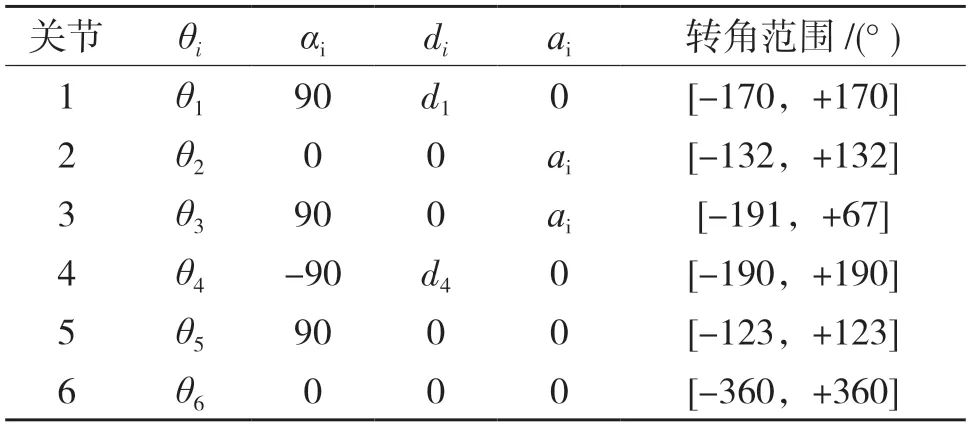
表1 机械臂D-H 参数表Tab.1 Robotic arm D-H parameters

已知关节1—关节6 的角度，即已知各关节坐标系对于基坐标系的位姿关系，则机械臂后一关节坐标系相对于前一关节坐标系的转换关系通式为：

由式（1）得各连杆转换矩阵如下：

机械臂总变换，即该末端端点的坐标系相对于该基坐标系的转换矩阵可表示为

验证正解。利用MATLAB 中的函数T=bot.fkine（zero），用Seriallink 函数得到矩阵为：

把初始关节角zero=[0 0 0 0 0 0] 代入式（2），可得矩阵0T6为

式（3）和式（4）相等，可得此机械臂正运动学求解正确。

用MATLAB 辅助模块机器人工具箱，搭建数学模型，调用Link 函数，采用标准D-H 参数，仿真模型如图3 所示。

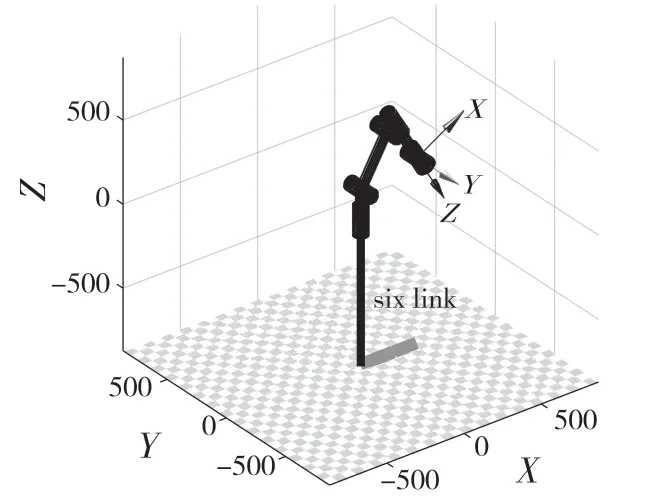
图3 机械臂连杆仿真图Fig.3 Simulation diagram of robot arm linkage

2 工作空间分析

工作空间是它的末端在每个旋转关节转角范围内能到达的所有位姿点的表示，它对机器人机械臂控制有重要意义。因此，不管是在机器人机械臂设计还是应用方面，都要对其工作空间进行分析。有4 种方法研究工作空间：解析法、图解法、数值法和蒙特卡洛法[10]。蒙特卡洛法是找到机械臂末端可达的区域边界，由边界线所组成的区域整合，然后在此区域内随机取点，得到随机取值点的集合，组成其工作空间。求解此机械臂工作空间的步骤如下:

（1）由式（2）解得位置向量0P6=[px py pz]；

（2）在每个旋转关节转角范围内选取随机步长变量：（θnmax-θnmin）rand（j）。有θn=θnmin+（θnmax-θnmin）rand（j）。其中，j=1，2，…，n；n=1，2，…，6。

（3）将步骤（2）中的θn代入正运动学方程，求得机械臂末端端点相对于极坐标系的位置点集合。迭代次数N的值越大，越能表达出机械臂实际工作空间的准确性。

（4）利用前3步在MATLAB里编程，然后运行，得到机械臂末端端点能达到的所有位置点，即工作空间图，取N=20 000，N=40 000，工作空间云如图4 所示。图5 为N=40 000 时的3 个方向投影图。

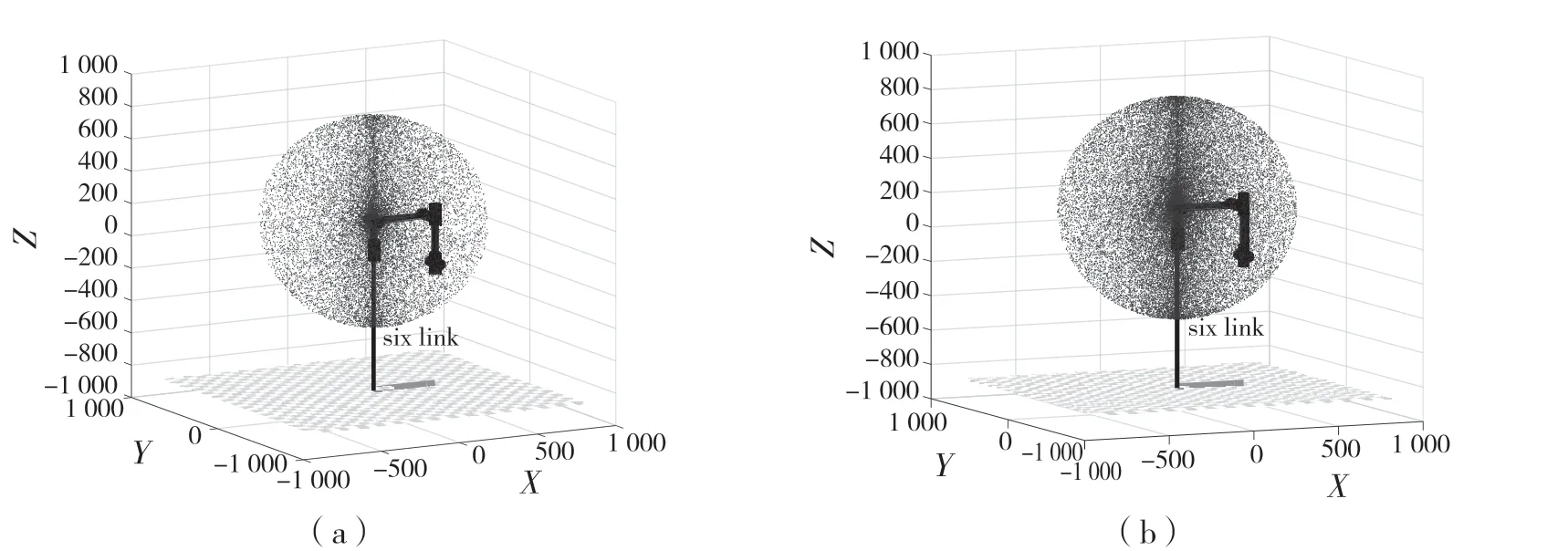
图4 不同迭代次数的工作空间云图Fig.4 Workspace cloud map for different iterations

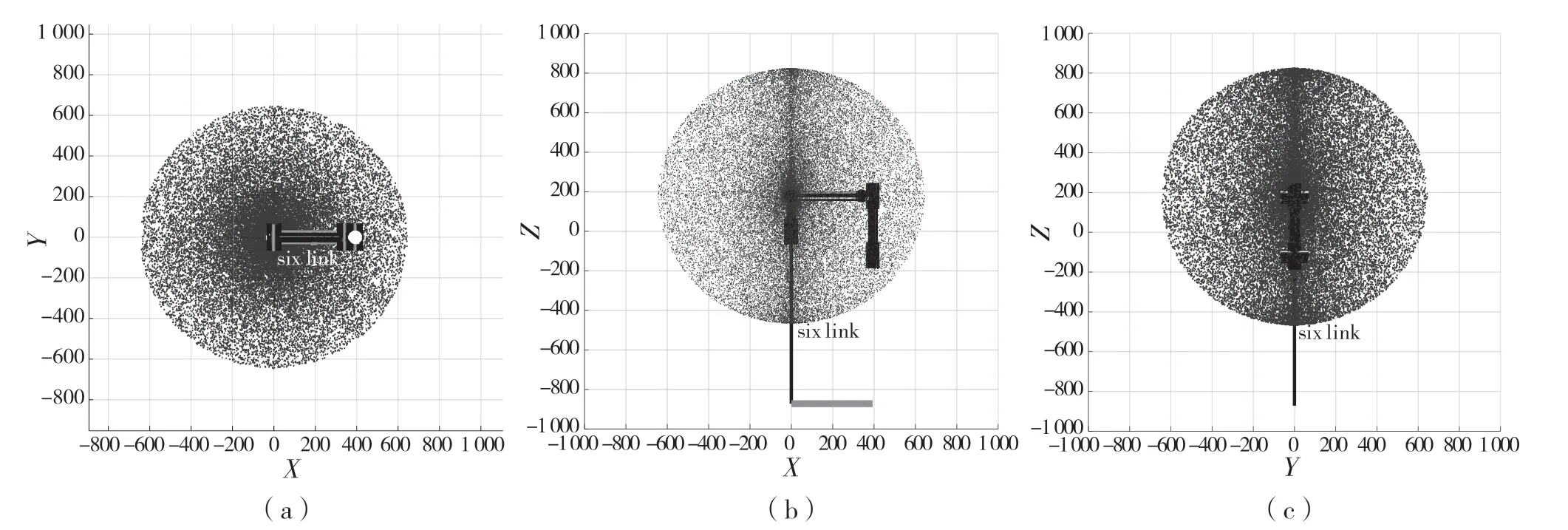
图5 N=40 000 时的工作空间云图Fig.5 Workspace cloud map at N=40 000

由图4 可知，此工作空间大体可看作椭球体，图形比较饱满，空间中能达到的尺寸符合此机械臂的关节参数，验证了所建机械臂对象的正确性，为之后的奇异性研究提供了试验基础。由图5 可知，各投影面图形分布均匀，无明显空洞，得到机械臂末端点在X轴方向运动的最大范围和最小范围到坐标原点的距离分别为640.8 mm 和-640.8 mm，在Y轴方向运动的最大范围和最小范围到坐标原点距离分别为642.7 mm 和-642.7 mm，在Z轴方向运动的最大范围和最小范围到坐标原点距离分别为823.6 mm 和-465.6 mm。

3 机械臂雅可比矩阵的求解

雅可比矩阵表达的是其关节速度和末端端点速度的微分运动关系，因此可利用微分变换法[11-12]求出雅可比矩阵。由于此桌面型607 机械臂有6 个旋转副，故只研究旋转关节的雅可比矩阵求解。

若用x=（x1，x2，…，xn）T表示其末端端点的位置向量，θ=（θ1，θ2，…，θn）T表示其关节向量，则x 与θ有如下关系：

对式（5）进行微分可得式（6）：

可得旋转变换的雅可比矩阵矢量表达式：

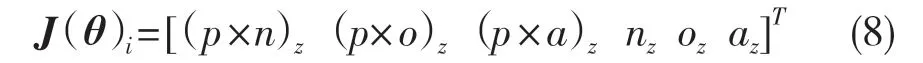
其中，（p×n）z=-pynx+pxny。同理可求（p×o）z及（p×a）z。

与关节6 的雅可比列矢量对应的变换矩阵为

分别将对应参数的n，o，a，p代入式（8），可得相应参数的雅可比矩阵的第6 列矢量：

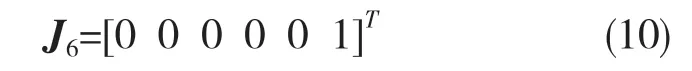
对于关节5，可在A6基础上求得其对应变换矩阵为

可求得关节5 对应的第5 列矢量：

对于关节4，在A5的基础上求得4T6：

分别将对应参数的n，o，a，p代入式（8），可得相应参数的雅可比矩阵的第4 列矢量：

同理可求出关节3、关节2、关节1 雅可比矩阵的列矢量如式（15）—式（16）：

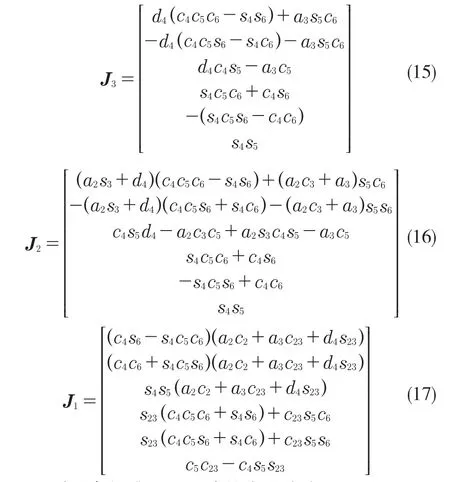
则可求得雅可比矩阵的表达式为

4 奇异位形识别与仿真

机械臂的奇异位置有边界奇异和内部奇异2种。一方面机械臂每个关节都有其运动范围，如表1 中机械臂的每个关节活动范围所示，在这些范围边界处则可能产生关节的运动极限位形，即奇异位形。当机械臂对应关节分别处于θ1=±170°，θ2=±13 2 °，θ3=±6 7 °/-191 °，θ4=±190 °，θ5=±123°，θ6=±360°这些极限位置时，对应位置为极限位置奇异点，此处只列出关节1 和关节2 的极限位置，用MATLAB 仿真模拟极限位置情况，仿真结果如图6 和图7 所示。

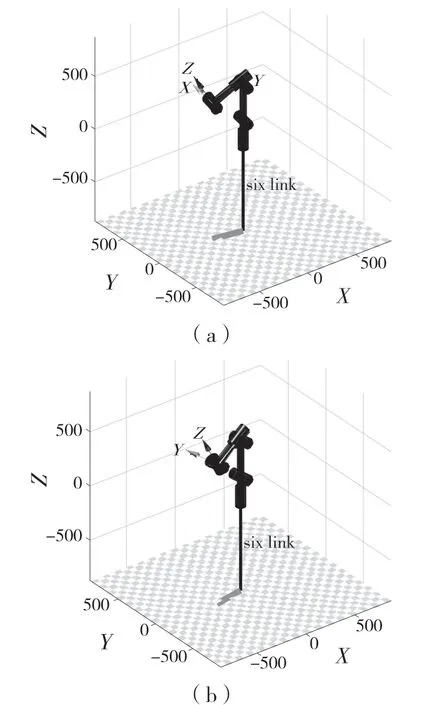
图6 关节1 边界奇异位形Fig.6 Boundary singular posture of Joint 1

图7 关节2 边界奇异位形Fig.7 Boundary singular posture of Joint 2

关于内部奇异位置，由于机械臂在内部奇异位置时雅可比矩阵的行列式为零，因此令行列式（18）为零可得其内部奇异位置。令│J（θ）│=0，得到

要使式（19）成立，则有以下3 类情形：

(1)当s5=0，即θ5=kπ。而θ5∈[-123 °，123°]。则θ5=0°。此种情形下，关节4 轴线与关节6 轴线处于共线状态，用MATLAB 工具箱进行仿真分析，如图8 所示，图9 为共线示意图。

图8 关节4 和关节6 轴线共线仿真图Fig.8 Collinear simulation diagram of axis of joint 4 and joint 6

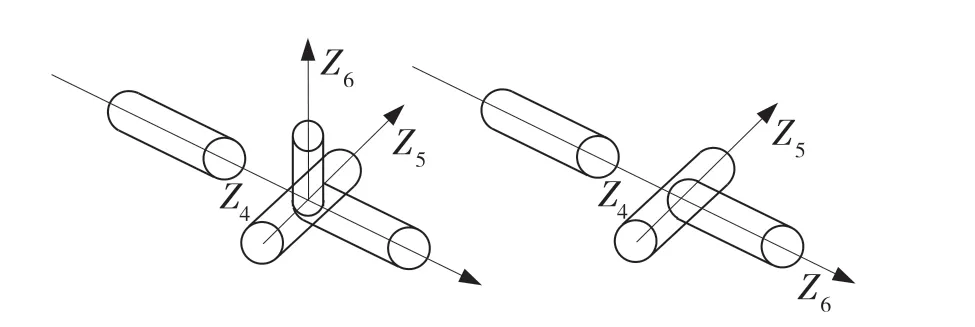
图9 关节4 和关节6 轴线共线示意图Fig.9 Collinear diagram of axis of Joint 4 and Joint 6

（2）当d4c3+a3s3=0 时，得则θ3=arctan（d4/a3）。将a3=53 mm，d4=300 mm 代入，得θ3=1.395 9°。此时关节4、关节5 和关节6 的运动轴线交点与关节2和关节3的轴线属于同一平面。运用MATLAB 对此奇异位形仿真，结果如图10 所示，图11 为示意图。

图10 关节4、关节5 和关节6 的运动轴线交点与关节2 和关节3 的轴线属于同一平面Fig.10 The intersections of motion axes of joint 4,joint 5 and joint 6 belong to the same plane as the axes of joint 2 and joint 3

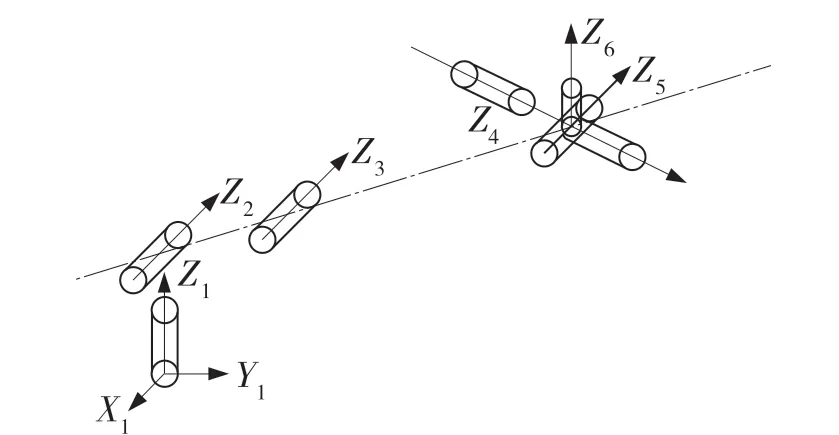
图11 示意图Fig.11 Schematic diagram

（3）当d1+a2c2+a3c（2-3）+d4s（2-3）=0 时，由于其关节2 轴线和关节3 轴线平行，所以关节1 轴线和关节4 轴线是共线的，用MATLAB 进行仿真，结果如图12 所示。图13 为关节1、关节4 和关节6轴线共线图。

图12 关节1、关节4 轴线重合Fig.12 Coincident axes of joint 1 and joint 4

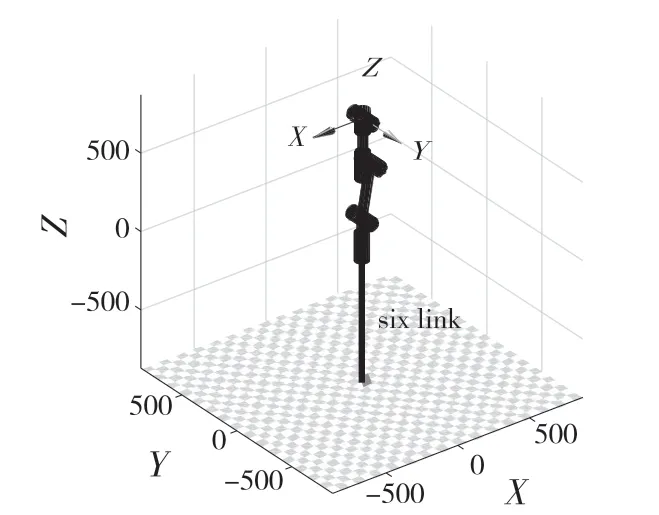
图13 关节1、关节4 和关节6 轴线共线图Fig.13 Collinear diagram of axes of joint 1,joint 4 and joint 6

5 结语

本文以桌面型607 串联机械臂为研究对象，首先运用标准的D-H 参数法求得其正运动学方程的解，并对其进行验证；其次，在MATLAB 中创建桌面型607 机械臂对象，研究其工作空间，得出其工作空间大体可看作椭球体，图形比较饱满，空间中能达到的尺寸符合此机械臂的关节参数，验证了所建机械臂对象的正确性，为之后的奇异性研究提供了试验基础；接着利用微分变换法求出该雅可比矩阵，最后利用该矩阵行列式等于0，求得其奇异位形，并用MATLAB 进行了仿真模拟，验证了方法的准确性。

通过分析仿真，此机械臂除了边界奇异点外，主要存在3 种内部奇异位形。本文分析研究可帮助此桌面型607 机器人机械臂在执行任务时避免出现奇异位形，对机械臂后续避免奇异位形算法研究提供参考。