基于ANSYS 的液压机悬挂夹紧装置结构优化

黄易周，贺福强，陈发江，徐浩然，万怡

（1.550025 贵州省 贵阳市 贵州大学 机械工程学院；2.550025 贵州省 贵阳市 贵州晶木建材有限公司）

0 引言

随着我国社会经济的高速发展，对木材的需求量逐年增加，使用农作物秸秆制造木质板材能够缓解木材资源匮乏的现状[1-2]。压制成型技术是木质板材制备过程中的一项关键技术[3]。木质板材压制成型的过程中，模具的合模与开模均在液压机上进行。本文所述液压机是在通用液压机上加装了一个悬挂夹紧装置，将模具上模部分夹紧并固定至液压机上，目的是降低模具运输成本，提高生产效率。

在类似的夹紧机构设计方面，张相志[4]等应用ADAMS 软件建立夹紧机构模型并对其进行运动学仿真，分析了运动过程中夹紧机构弹簧的受力情况；裴峻峰[5]等应用ANSYS 软件对套管钳钳头夹紧机构的三维模型进行了力学分析，并使用压力胶片测量方法进行了应力测试分析，验证了设计仿真的正确性；翟靖[6]等研制了一种专用于动力电池的夹紧机构，并通过SolidWorks 软件对夹紧过程中的关键组件进行了有限元分析，形成了结构优化的受力件，有效解决了移动版组件上翘的难题。

目前应用的液压机用悬挂夹紧装置主要根据以往经验进行设计，虽然能够满足使用要求，但是为保证其强度，结构上存在一定的冗余，因此希望对其进行轻量化设计。拓扑优化设计是根据有限元分析结果对结构材料进行删除，寻求设计结构材料最佳分配的优化方法[7-9]。但拓扑结构优化的结果通常不能直接应用，需要进行一定的尺寸优化才能得到最终结果。响应面法[10]是一种数学方法和统计方法结合的产物，用于解决非线性数据处理的相关问题，通过对过程的回归拟合[11]、响应曲面分析[12]和等高线的绘制求出相应于各因素水平的响应值，最后基于响应值找出预测结果的响应最优值。

本文以液压机中的悬挂夹紧装置为研究对象，使用ANSYS 软件对其进行静力学分析及拓扑结构优化，并确定4 个尺寸变量，然后用响应面法对尺寸变量进行优化分析，最后验证了优化结果，使改进后的悬挂夹紧装置更好地满足设计要求。

1 工作原理

该液压机的物理样机如图1 所示，为方便说明，现用UG 软件对液压机的悬挂夹紧装置及相关零件进行模型的建立，如图2 所示。悬挂夹紧装置的工作分为2 部分：一是模具开模阶段，液压缸推动悬挂夹紧装置将模具上模部分与液压机上压板固定在一起，然后模具上模部分与液压机上压板一起向上运动完成开模；二是模具合模阶段，模具上模部分与液压机上压板在液压缸作用下一起向下压，直到压制至指定位置后，悬挂夹紧装置解锁，然后将模具与产品一起移出液压机，进行下一个工序。

图1 液压机实物图Fig.1 Hydraulic press

图2 悬挂夹紧装置示意图Fig.2 Schematic diagram of suspension clamping device

2 悬挂夹紧装置拓扑优化

为了使悬挂夹紧装置的结构合理性得到提升，可以使用拓扑优化的方式对悬挂夹紧装置进行优化。拓扑优化的研究已经较为成熟，目前有多款商用优化软件均有拓扑优化模块，综合考虑各软件操作难度、兼容性以及优化目的，本文采用 ANSYS软件的拓扑优化模块对该悬挂夹紧装置进行优化。主要考虑该悬挂夹紧装置在吊起模具上模部分时的受力状态，对其结构形式进行改进，使其更加轻便，同时更符合受力分布情况。优化流程如图3 所示。

图3 拓扑优化流程图Fig.3 Topology optimization flowchart

2.1 悬挂夹紧装置静力学分析

ANSYS 软件中，对零件进行静力学分析的流程主要包括模型建立、材料赋予、网格划分、施加载荷以及边界条件设置。悬挂夹紧装置的模型已经在UG 软件中建立，可直接使用ANSYS 软件与UG软件的接口调用该模型。该装置的材料选用铸钢，其主要力学参数为：弹性模量2.02×105MPa，泊松比0.3，屈服强度345 MPa。载荷以及边界条件的施加可通过ANSYS 软件中的Load 和Support 工具对模型中的受力点及铰点进行操作，按照实际的工况施加一定的载荷及边界条件。

ANSYS 常用的有四面体网格划分、六面体为主网格划分、自动网格划分、扫掠网格划分等。由于本文中零件较为复杂，故优先考虑自动网格划分方式。但是该方式划分出的网格中包含大量非必要的四面体网格，该类型网格在同等尺寸下较六面体网格的网格单元数量及网格节点数量多得多，需要采用高阶单元，这会造成软件求解时间大大增加，且计算精度也较六面体网格差一些，因此本文采用分割几何体的方法，将悬挂夹紧装置进行一定的分割，对其不同的区域采用不同的方式进行网格划分，具体划分结果如图4 所示。其中，除中间梁部分、肋板部分及两边连接部分采用六面体为主的网格划分方式，其余部分采用扫掠网格划分方式。

图4 网格划分方式Fig.4 Meshing mode

除了网格划分方式外，网格密度也是影响有限元计算的一个关键因素。网格密度过高，单元和节点数量巨大，求解时间会变得很长；降低网格密度，虽然能使单元节点数目减少，相应的求解时间减少，但计算结果误差会增大。为了平衡求解的可信度和速度，必须要选择适中的网格单元数量进行计算，为此先对该悬挂夹紧装置进行多种方式的网格密度划分并进行静力学分析，寻找合适的网格密度。网格划分应在满足计算精度的情况下尽可能选择较少数量的网格。由图5 可知，当网格单元数量小于100 000 时，最大等效应力呈波动性上升的趋势；而当网格单元数量大于100 000 时，最大等效应力达到最大值并基本趋于稳定，因此，最终选择的网格划分方式为：网格大小4 mm，网格节点数量483 686，网格单元数量131 359。基于该网格划分方式的静力学仿真结果如图6 所示，最大等效应力169.55 MPa，小于材料屈服强度345 MPa。

图5 最大等效应力与网格密度关系图Fig.5 Diagram of maximum equivalent stress and mesh density

图6 静力学仿真结果Fig.6 Statics simulation results

2.2 结构拓扑优化

将静力学仿真的参数设置及结果与拓扑优化模块进行同步，并设置拓扑优化参数，最大迭代次数为300 次，收敛精度为0.1%，质量削减率为50%，并在拓扑优化模块中进行迭代计算，最终解算结果如图7 所示。根据图7 中的拓扑优化结果，将悬挂夹紧装置中存在浪费的位置进行删减，重新建立其模型，结构如图8 所示。

图7 拓扑结构优化结果Fig.7 Topology optimization results

图8 新结构模型图Fig.8 New structure model diagram

3 悬挂夹紧装置尺寸优化

3.1 变量设置

以距底边220 mm 为起点在零件上开通孔，长度a为第1 个变量，宽度b为第2 个变量；另外，在同一个面上开等边三角形通孔，其与外边框的距离和与转角处的距离c为第3 个变量，等边三角形的边长d为第4 个变量，具体如图9 所示。

图9 变量设置示意图Fig.9 Schematic diagram of variable setting

3.2 响应面分析

本文采用Box-Benhnken 原理进行仿真实验设计，响应面水平见表1，响应面实验设计方案见表2。

表1 响应面试验设计因素水平表Tab.1 Response surface test design factor level

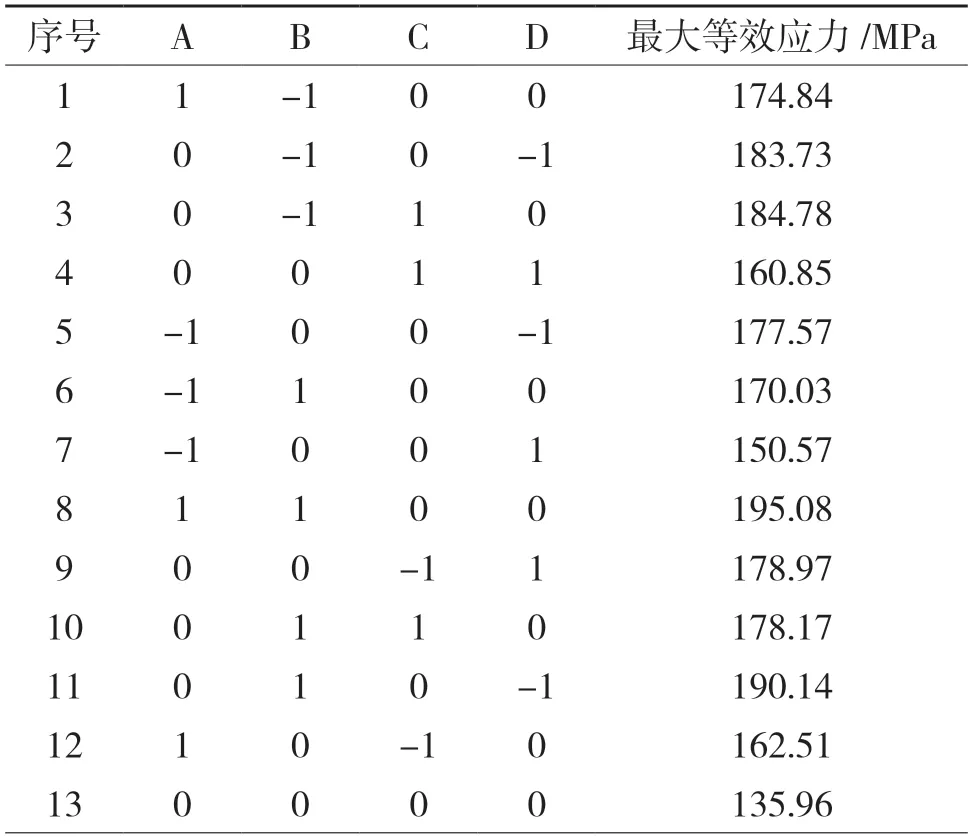
表2 响应面试验设计及试验结果Tab.2 Response surface test design and test results

（续表）

利用Design-Expert软件进行响应面回归分析，得到尺寸a、b、c、d与最大等效应力之间的二次多项式回归方程如式（1）所示：

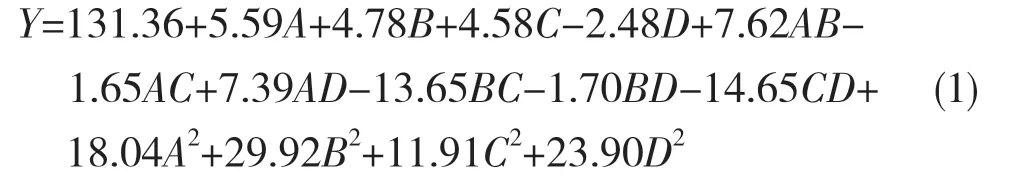
对回归方程进行方差分析，结果如表3 所示。

表3 响应面回归模型方差分析Tab.3 Response surface regression model variance analysis

其方差分析的P值＜0.000 1，表明该模型对最大等效应力的影响较显著。失拟项F值为2.97，P值为0.152 7，表明该方程的失拟项不显著，方程拟合程度高，具有较高的可信度。该方程模型中的一次项A、B、C显著D不显著，表明尺寸a、b、c对最大等效应力有较显著的影响，其显著性的顺序为：尺寸a＞尺寸b＞尺寸c。二次项AB、BC、CD显著，表明除了各尺寸对最大等效应力有影响外，它们之间还有一定的交互作用。

图10—图15 是各因素交互作用对最大等效应力影响的响应面图。

图10 尺寸a 和尺寸b 的交互作用对最大等效应力的影响Fig.10 Effect of interaction of dimension a and dimension b on the maximum equivalent stress

图11 尺寸a 和尺寸c 的交互作用对最大等效应力的影响Fig.11 Effect of interaction of dimension a and dimension c on the maximum equivalent stress

图12 尺寸a 和尺寸d 的交互作用对最大等效应力的影响Fig.12 Effect of interaction of dimension a and dimension d on the maximum equivalent stress

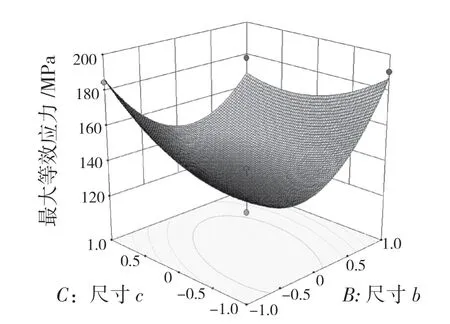
图13 尺寸b 和尺寸c 的交互作用对最大等效应力的影响Fig.13 Effect of interaction of dimension b and dimension c on the maximum equivalent stress

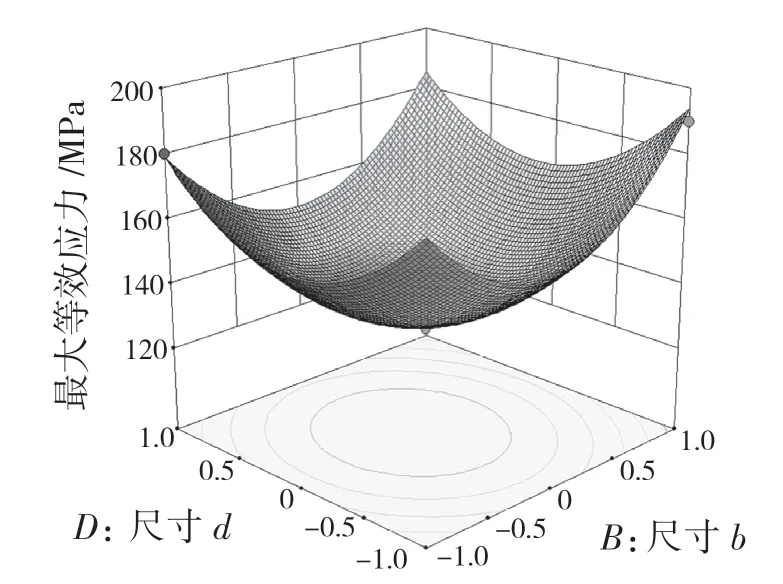
图14 尺寸b 和尺寸d 的交互作用对最大等效应力的影响Fig.14 Effect of interaction of dimension b and dimension d on the maximum equivalent stress

图15 尺寸c 和尺寸d 的交互作用对最大等效应力的影响Fig.15 Effect of interaction of dimension c and dimension d on the maximum equivalent stress

响应面图中，可以通过曲面倾斜度确定某因素对结果的影响程度，曲面倾斜度越高说明该因素对结果的影响程度越显著。响应曲面图投影若为圆形，说明两因素交互对结果的影响很小；响应曲面投影若为椭圆形，说明两因素交互对结果的影响显著。从图中可以看出，尺寸a与尺寸b之间、尺寸b与尺寸c之间、尺寸c与尺寸d之间均有较明显的交互作用，说明它们对最大等效应力的影响较为显著。交互作用对最大等效应力的影响顺序为：CD＞BC＞AB，结果与表3 中P值得出的结果相符。4 个因素间的响应曲面均存在极值点，说明最大等效应力在当前各个因素的水平范围内存在最小值。

分析可知，当零件尺寸分别为a=97.2 mm，b=38.7 mm，c=8.55 mm，d=39.8 mm 时，最大等效应力存在最小值，其预测值为130.04 MPa。为验证该结果，将上述尺寸导入ANSYS 中进行分析，得到的最大等效应力为132.39 MPa，与预测值误差为1.8%，因此利用响应面法对该悬挂夹紧装置进行尺寸优化是可行的。

4 结论

对液压机的悬挂夹紧装置进行了轻量化设计，得到如下结论：

（1）不同的网格划分方式与网格密度都会对有限元仿真的造成一定影响。本文针对悬挂夹紧装置不同几何特性的部位选择了不同的网格划分方式。此外，对于特定零件，有限元计算结果会随网格密度提高逐渐趋于稳定，在达到某个临界值后，即使再提高网格密度，计算结果也不会有太大的变化。该临界值可以作为悬挂夹紧装置网格密度的参考，在满足计算精度的前提下提高分析效率。

（2）采用响应面分析的方法可建立悬挂夹紧装置最大等效应力与各尺寸变量间的二次多项式回归方程，根据回归方程求得最大等效应力最小值的预测值130.04 MPa 及其对应的各尺寸变量。将各尺寸变量导入ANSYS 进行静力学分析，结果与预测值误差仅为1.8%，说明使用响应面法对悬挂夹紧装置进行尺寸优化是可行的。

（3）利用拓扑优化与响应面分析相结合的方法可以较好地实现结构的轻量化设计。悬挂夹紧装置在优化以后质量减轻16.8%，最大等效应力减少21.9%。