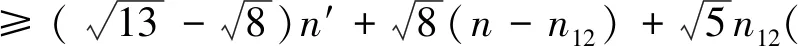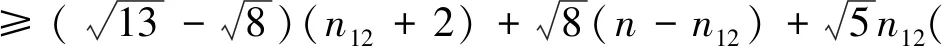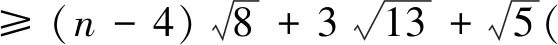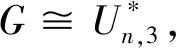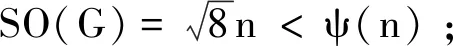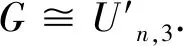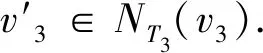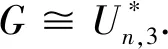单圈图的Sombor指标
2022-10-31胡文洁高珊杨星光
胡文洁,高珊,杨星光
(1.湖北大学数学与统计学学院,湖北 武汉 430062;2.湖北大学计算机与信息工程学院,湖北 武汉 430062;3.应用数学湖北省重点实验室(湖北大学),湖北 武汉 430062)
0 引言
设图G=(V,E)是一个简单无向连通图.图G的点数|G|称为G的阶.G的边数记为‖G‖.对图G中任意的点v,用NG(v)表示点v在图G中的所有邻点的集合.点v在图G中的度dG(v)(简记为d(v))指G中与v关联的边的条数, 即dG(v)=|NG(v)|.如果d(v)=maxvi∈Vd(vi),那么称v是图G中的最大度点. 图G的度为1的点称为G的悬挂点, 与悬挂点关联的边称为G的悬挂边.我们用G-x或G-xy分别表示删去x∈V(G)或xy∈E(G)后得到的图.同样地,G+xy表示在G的不相邻两点x,y之间添加一条边后得到的图.
令G和H是两个简单连通图,且u∈V(G),v∈V(H).把u和v粘合在一起得到的图记为GuvH,或简记为GuH.
满足‖G‖=|G|-1的连通图称为树.满足‖G‖=|G|的连通图称为单圈图. 记Un是所有n阶单圈图的集合.记Cn,Pn,Sn分别为n阶圈,n阶路和n阶星.Sn的最大度点称为Sn的中心.
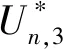
图G的Sombor指标定义为
图G的Sombor指标是由Gutman I.[2]基于图G的边的端点的度提出的一种新的拓扑指标.Sombor指标自提出以来,受到广大学者的关注,得到许多新的研究成果[1-5].2021年,Cruz-Rada[1]得到了单圈图和双圈图的Sombor指标的极值,Gutman I.[2]给出了Sombor指标的一些性质,分别刻画了连通图的Somber指标的极值和极图.最近,Wang-Zhang[3]刻画了给定直径的树的Sombor指标的极值和极图.Zhou-Lin-Miao[4-5]分别给出了给定匹配数和最大度的单圈图的Sombor指标的极值,并刻画了对应的极图.
本文中,我们进一步研究单圈图的Sombor指标,得到了n阶单圈图第二大和第二小时的Sombor指标的值,并刻画了Sombor指标达到第二大和第二小时的极图.
1 相关引理
本节中,我们给出几个在主要结论证明中需要用到的引理.
引理1.1[2]令G是一个图,且u∈V(G),v是星图Sr的中心,w是Sr的悬挂点,则
SO(GuwSr) 引理1.2设G是一个图,如果xy∉E(G),yz∈E(G).令G*=G-yz+xy.如果dG(x)≥dG(z),那么SO(G) 引理1.2的证明由r>0,y2>(y-r)2,可得 因此g(r)(x,y)是关于x≥1的递增函数,也是关于y≥1的递增函数. 设G是一个图,我们定义x≻Gz当且仅当dG(x)≥dG(z),dG(x′)≤dG(z′),对任意x′∈NG(x){z}和z′∈NG(z){x}. 引理1.3设G是一个图,u,v∈V(G).令Gp,r(p≥1,r≥1)是图G两个点u,v处分别粘上p,r条悬挂边后得到的图, 则或者SO(Gp,r) 引理1.3的证明设u′,v′是Gp,r的两个悬挂点,且uu′∈E(Gp,r),vv′∈E(Gp,r),则Gp+1,r-1≅Gp,r-vv′+uv′,且Gp-1,r+1≅Gp,r-uu′+vu′.如果dGp,r(u)≥dGp,r(v),则由引理1.2可知SO(Gp,r) Cruz-Rada[1]分别刻画了n阶单圈图的Sombor指标达到最大和最小时的极图,并给出了下面的结果. 定理2.1[1]如果G∈Un, 那么 SO(Cn)≤SO(G)≤SO(Un,3). 下面我们进一步考虑n阶单圈图的Sombor指标.注意到U3={C3},U4={C4,U4,3}.由定理2.1可知,SO(C4) 对任意的图G∈Un,令Cg=v1v2vgv1是G中唯一圈.令Ti为G-E(Cg)的包含vi(1≤i≤g)的分支.则Ti是一棵以vi为根点的树,其中1≤i≤g.如果|Ti|>1, 称Ti是非平凡的. 定理2.2设G∈Un{Cn}.则 SO(G)≥φ(n) (1) 而且不等式中等式成立当且仅当G∈Ln. SO(G)≥φ(n), 且等式成立时仅有G∈Ln. 先给出下面记号: E′=∪i+j≥5Eij, Eij={uv∈E(G):dG(u)=i,dG(v)=j}. 记nij=|Eij|,n′=|E′|,则n=n12+n13+n22+n′, 且 (2) 且不等式中等式成立时仅有E′=E23. 因为GCn,故g≤n-1,且Cg中至少存在一个度为3的点. 于是|E′∩E(Cg)|≥2.接下来证明下面命题. 命题1n′≥n12+2,进而n′≥3或n13≥1. 命题1的证明因为g≤n-1,故G-E(Cg)存在非平凡分支Ti.如果E12=Ø,那么viw∈E′或viw∈E13,其中w是vi在Ti中的邻点,即n′≥3或n13≥1.因此不妨假设E12≠Ø.令φ为E12到E′E(Cg)的映射.对任意的uv∈E12,dG(v)=2,dG(u)=1.不妨假设uv∈E(Tl)(1≤l≤g),则Tl中存在唯一(v,vl)-路P.设vl在P上的邻点为w,则vlw∈E′E(Cg).若Tl中存在度≥3的点,在Tl中唯一的(v,vl)-路P上选取离v最近的3度点设为x,P上到v距离比d(x,v)小1的点记作y,即φ是单射.从而|E′E(Cg)|≥|E12|,即n′≥n12+2≥3. 我们考虑如下两种情形: 情形1:n12≥1. 在此情形下,由命题1可知n′≥n12+2.由(2)式可得 =φ(n). 上式等式成立时,n12=1,n′=n12,n13=0,且不等式(2)中等式成立, 因此G∈Ln. 情形2:n12=0. 在此情形下,由命题1可知n′≥3或n′=2,n13≥1.由(2)式可知 =φ(n). 综合情形1和情形2的证明,我们完成了定理2.2的证明. 定理2.3令G∈Un{Un,3}.则 SO(G)≤ψ(n) (3) =ψ(n). 将SO(G)看作关于g的函数 由函数的单调性和引理1.4可得函数关于g单调递减.则 <ψ(n). 因此下面不妨假设g≤n-1且当g≥4时,GUn,g. 先证明如下命题. 命题2g=3. 命题2的证明如果g≥4, 则GUn,g.设dG(v1)=max{dG(vi):1≤i≤g},因为g≤n-1,故dG(v1)≥3.令G′=G-v2v3+v1v3,则G′∈Un{Un,3}.注意到dG(v1)≥dG(v2).因此由引理2.2,SO(G′)>SO(G),与G的取法矛盾. 于是g=3. 接下来考虑如下两种情形. 情形1:G-E(Cg)中存在唯一的非平凡分支. =ψ(n). 情形2:G-E(Cg)至少包含两个非平凡分支.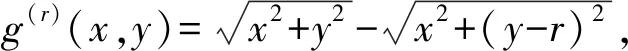

2 主要结论