基于扩展卡尔曼滤波的车辆运动轨迹估计方法研究

龙杜辉

（200082 上海市 上海理工大学机械工程学院）

0 引言

目前车辆上使用的定位技术主要有全球定位系统（GPS）、航位定位系统（DR）、惯性导航系统（INS）和同时定位与建图（SLAM）。GPS 具有全球性、精度高等特点，但是受外界干扰最大；DR 利用车载的传感器测量车辆的车速、加速度、偏航角速度来实现车辆的自主定位。在短时间内，DR 精度是很高的,但由于累计误差的存在，经过一段时间后，定位系统就会失效；INS 跟DR 一样短时间的精度高，但是定位误差会随时间累积[1-2]；SLAM 通过雷达或相机对周围环境进行扫描，来估计自身的位置，但是随着环境的几何特征和纹理特征的不明显，定位也会失效，而且SLAM 使用的传感器成本比较高[3]。每一种传感器进行定位都有优点，同时也存在弊端。利用多传感器的信息融合估算运动轨迹，可以避免单一传感器定位的弊端。本文利用扩展卡尔曼滤波器对车载编码器和IMU 采集的信息进行融合，实现车辆的自主定位，对比融合后的轨迹和真实轨迹，证明了该方法的有效性。

1 差速模型的建立

本文实验对象是两后轮独立驱动的小车模型，如图1 所示，它能通过调节两轮的速度差达到转弯目的，这种运动模型叫做双轮差分驱动模型[4]。

图1 小车模型Fig.1 Car model

小车的原点位于两轮轴的中心位置。用该模型估算小车位置只需2 个主要参数：车轮之间的距离d 和车轮半径R。运动模型如图2 所示，一般情况下，通过两车轮上编码器测量每个时间步长δt 的左右车轮转过角度δψL、δψR计算小车位姿的变化。假设x 正方向为小车前进的方向，小车左边为y 正方向，z 的正方向垂直于小车向上。因此各运动状态下模型如式（1）—式（7）。

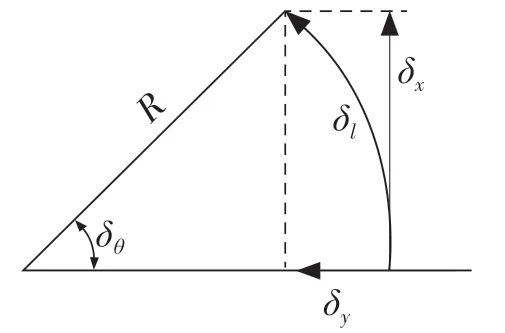
图2 运动模型Fig.2 Motion model

直行时：

转弯时：

小车运动方式通过局部位姿增量进行改变，累加局部位姿增量即可得到小车的运动轨迹，因此利用小车的编码器数据获得了车辆的里程计模型。由于车辆运动累积具有不确定性，需要协方差矩阵Q 来表示这种不确定性关系，它可以通过两驱动轮转角测量值的不确定性来如式（8）表示：

式中：J——运动模型的雅可比矩阵；Qη——轮子角度测量值的协方差。

2 IMU 驱动模型的建立

IMU 由加速计和陀螺仪组成[5]，它能测量车辆的线加速度as和角速率ωs。通过IMU 得到的线加速度和角速率可以用来预测小车位姿。式（9）为IMU 计算的状态量和误差，式（10）—式（14）为状态量和误差更新过程。

式中：p，v，q ——惯性测量单元的参考系的位置、速度和方向四元数；ab，ωb——加速度计和陀螺仪的偏差；vi，θi——在时间间隔Δt 内的测量误差；ai，ωi——加速度计和陀螺仪偏差的随机游走。——四元数相乘，R{q}——关于方向角q 的旋转矩阵，这里仅考虑2D 情况下，则R{q}如式（15）所示：

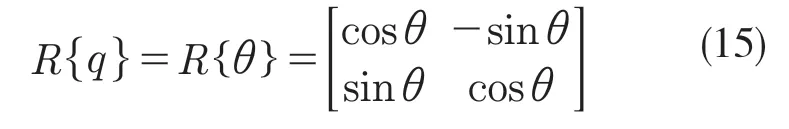
3 基于扩展卡尔曼滤波的车辆位置预测

3.1 扩展卡尔曼滤波器

扩展卡尔曼滤波器[6]是在卡尔曼滤波基础上进行改进，使其适用于非线性系统。主要应用的方法是在上一时刻的后验估计状态量下进行泰勒展开得到这附近的线性系统，然后再对系统状态进行估计。扩展卡尔曼滤波分为预测和更新2 个部分，如图3 所示。

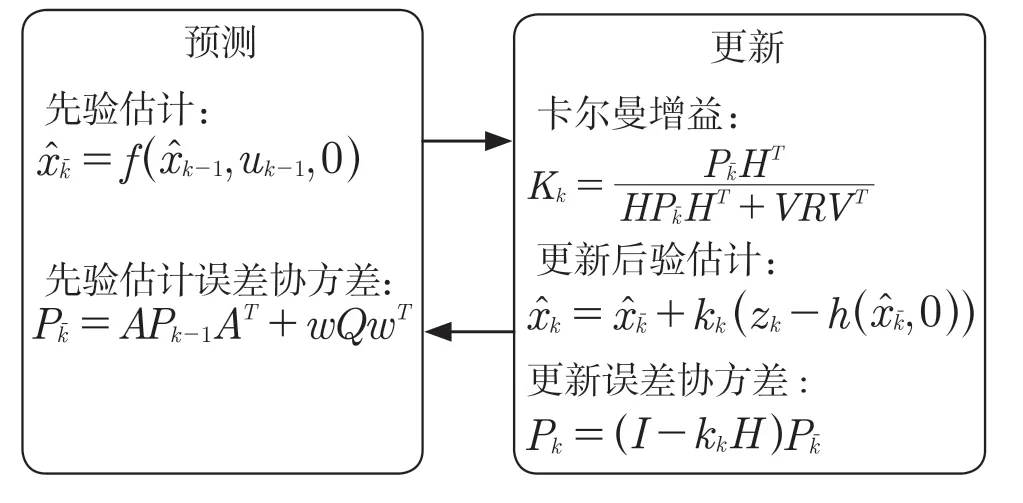
图3 扩展卡尔曼滤波过程Fig.3 Extended Kalman filtering process

3.2 多传感信息融合

由于惯性测量单元IMU 估算的车辆的运动轨迹相对于编码器的估算来说在短时间内准确度更高，但由于IMU 中加速度计和陀螺仪的双重误差累积，在长时间的运作下，对车辆的定位准确度明显下降，此时应更相信由车轮编码器估算的轨迹。

为此，提出了一种基于信息融合的扩展卡尔曼滤波器策略，来精准定位车辆位置和轨迹预测方法。此系统同时接收来自编码器信息以及惯性测量单元的数据。通过组合定位系统的数学模型，可以融合两个系统的数据，获得车辆位置的精准估计。融合过程的流程图如图4 所示。

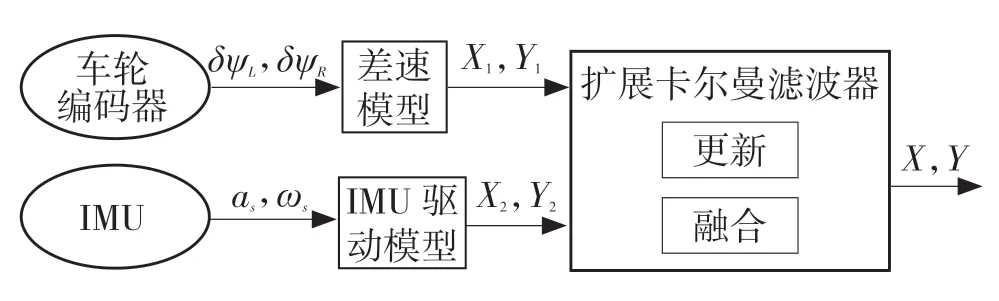
图4 多传感数据融合过程Fig.4 Multi-sensor data fusion process

多传感的数据融合可以将其中一个传感器的数据作为测量量，另外一个传感器的数据当作观测量进行融合[7]。以下为多传感的融合模型。

（1）以车轮编码器数据作为预测模型：

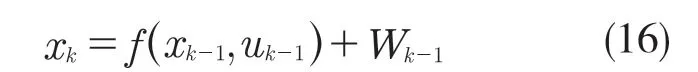
式中：xk=[xo，yo，θo]T——车辆在k 时刻平面坐标及转角的三维向量；f ——k-1 时刻与状态向量xk-1、系统控制输入量uk-1有关的非线性函数；Wk-1——系统在k-1 时刻的高斯白噪声，呈正态分布。

（2）以惯性测量单元数据作为观测模型：

式中：zk=[xi，yi，θi]T——k 时刻三维的观测向量；h——k 时刻关于状态向量xk、系统控制输入量vk的非线性函数；Vk——系统在k 时刻的观测噪声，呈高斯正态分布。

3.3 定位评价标准

评价一种算法设立评价标准是必要的[8]。本文采用定位误差和定位的成功率作为评价准则，其方法如下：

3.3.1 定位误差

定位误差表示估计位置与真实位置偏差，表达式为：

式中：d——使用融合算法后的位置与真实位置的偏差；xe、ye——通过融合算法估计的车辆坐标；xt、yt——此时刻车辆真实坐标。

3.3.2 定位准确率

定义当使用融合算法后与真实位置的偏差d 小于车辆的1/5 时为定位成功，否则设为定位失效。这里使用的小车模型长宽都为38 cm，故取判断定位成功的阈值为7.6 cm。定位准确率即为定位成功次数与实验测量总数的比值：

4 实验验证

本文基于ROS 操作系统中gazebo 的仿真环境，完成车辆行驶的仿真实验。传感器数据由gazebo环境中，小车上传感器插件模型提供话题数据，将IMU 和差速模型得到的里程计数据在ROS 的工作空间中进行融合，得到融合后的话题数据，将这些话题打包成bag 文件，并导入MATLAB 软件，结果如下所示。

图5 中，小车从图5（a）依次运动到图5（d）。由图6 可知，由多传感融合算法估计出来的轨迹与真实轨迹是十分接近的，在抖动区间也能准确预测真实轨迹。

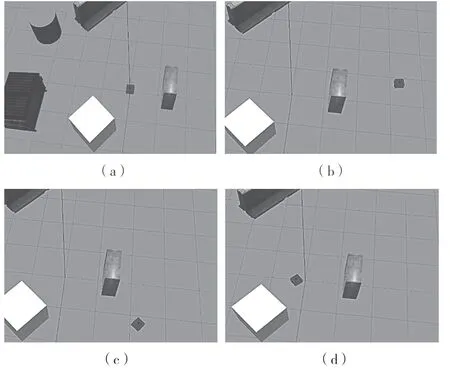
图5 小车在gazebo 运动过程Fig.5 Movement of trolley in Gazebo

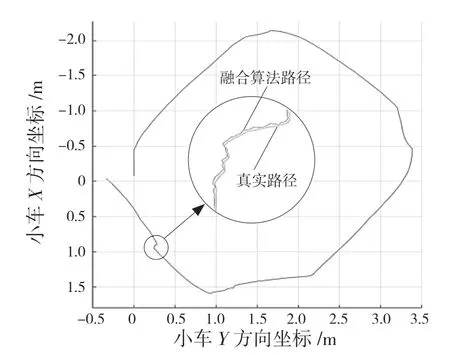
图6 小车运动轨迹Fig.6 Trajectory of trolley

为了定量判断扩展卡尔曼滤波器对多传感融合的定位效果，在所有的数据点中随机依次抽取10 个测量点作为判断指标，分别与真实值进行比较，处理后的数据如图7—图9 所示。

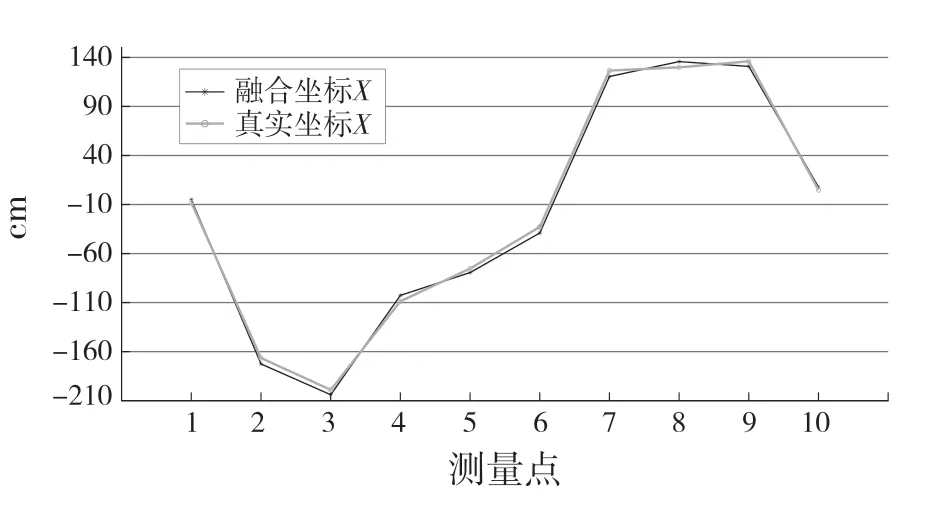
图7 小车X 轴方向上对比Fig.7 Comparison of trolley in X-axis direction

图8 小车Y 轴方向上对比Fig.8 Comparison of trolley in Y-axis direction

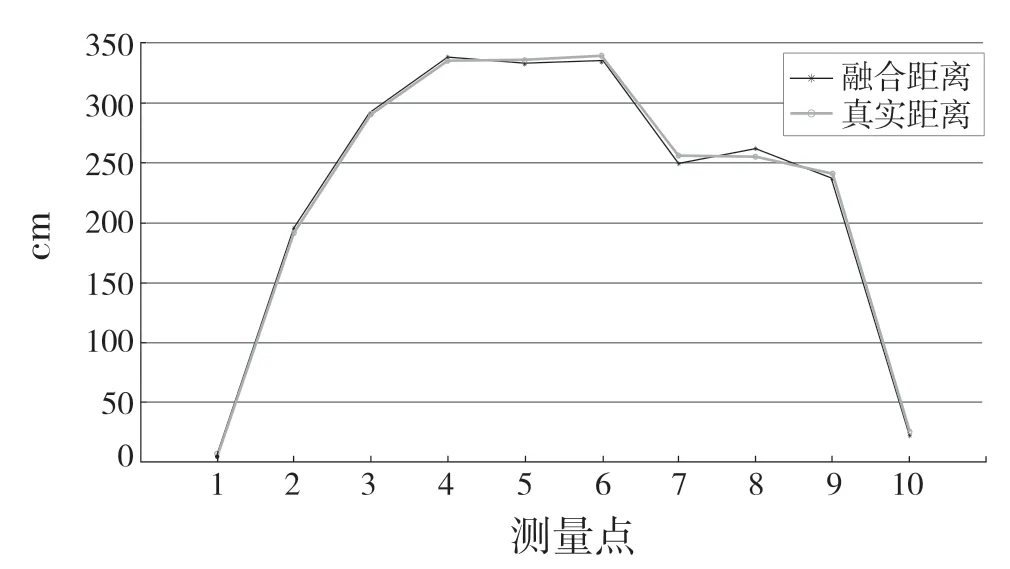
图9 小车与原点距离对比Fig.9 Comparison of the distance between trolley and origin

根据定位评价标准对该实验结果进行分析。由图10 可知，在随机的10 个测量点中只有测量点4 和测量点6 大于判断阈值，故定位失败。由式（20）可得小车在本次实验的定位成功率μ=80%。

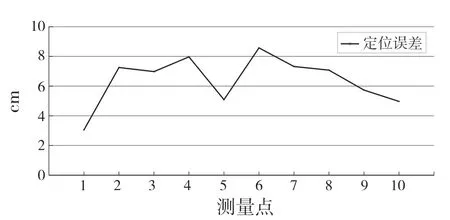
图10 定位误差分析Fig.10 Positioning error analysis

由于卡尔曼滤波器只利用了上一时刻的数据和系统的输入量，计算量是比较小的，所以相比于其它算法而言，实时性和鲁棒性都是比较优异的。

5 结论

（1）本文以小车模型为研究对象，针对车辆定位容易失效的问题。通过利用扩展卡尔曼滤波对编码器和IMU 数据进行融合，提高了定位的准确性，实现了自主定位。

（2）通过对定位误差的定量分析，验证了本文算法对提高车辆定位是有效的，并且可以仅通过车载传感器实现自我定位，解决了在复杂环境下定位失效的困惑。

（3）本次研究也存在许多不足的地方。首先本次实验是基于仿真的，故误差设定会比较不合理，设定编码器和IMU误差类型均符合高斯正态分布，这与实际误差存在着差异，且设定的方差比较小；其次仿真的模型小车与真实车辆也存在一定的差异。后续研究可以考虑采用真实的模型进行实验验证，然后加入相机、雷达进行多传感融合，继续提高定位进度。