从“联”向“变”：数学整体性教学的有效策略

江苏省苏州市吴中区华东师范大学苏州湾实验小学 皋 岭

系统论认为，人们对事物的认知具有整体性。所谓“整体性”，简而言之就是“整体大于部分之和”，即它不仅表示包含事物各部分或要素的个体特性，还表示事物各部分或要素个体特性之和以外的整体特性。基于整体性视角，我们在数学教学过程中，要充分发掘各部分或要素之间存在的关联，催生单一部分或单个要素不具备的整体性变化，追求“1+1＞2”的教学效果。为此，从“关联”趋向“变化”就成了开展数学整体性教学的有效策略，也成为促进学生形成与发展数学核心素养的重要保障。

一、分析缺“联”少“变”的教学现象

（一）只见树木，不见森林

在义务教育阶段数学课程内容的实施过程中，教师往往采用分课时的方式，把相关联的数学课程内容拆分成一个个分散的“点”来进行组织教学。一些对课程内容缺乏整体把握的教师，不能抓住课程内容各部分之间的关联与变化，人为割裂课程内容的整体性，使得数学课程的实施“只见树木，不见森林”。如教师就点教点，每个教学课时仅对单一知识点进行教学与训练，缺乏与相关知识点的关联，从而形成“碎片化”的教学样态；就题论题，不在类似数学问题的联系与变化中，揭示一类问题背后所蕴藏的相通的数学思想方法，而是采用“孤立化”的教学方式；就方法讲方法，对待数学方法的多样化与优化问题缺少整体视角，最终形成“单一化”的解决问题的方法。

（二）捡了“芝麻”，丢了“西瓜”

数学教材编制的课程内容，以单元为单位，通过例题、练习等方式呈现学生探索的数学问题，并且通过大量配套的例题与练习，把需要学生锻炼形成的数学核心素养隐含其中。数学课堂教学如果仅仅为了得到一道道例题与练习的正确答案，而忽略发掘例题与练习背后关联着的数学思想方法，缺少对零散教学内容关联与变化的整体提炼，将会使学生停留在数学学习的表层，而无法达到数学思想方法上的底层贯通。那么，发展学生的数学核心素养终究会是一句空话。正如，我们捡了完成一道道例题与练习教学表层的“芝麻”，却丢了这些例题与练习教学深层的“西瓜”。

（三）坐而论道，纸上谈兵

小学是学生系统学习数学的起始阶段，小学阶段的数学学习内容与学生实际生活有着广泛的联系。因此，在数学课程的实施过程中，教师要十分重视让学生在解决日常生活中的数学问题的同时，增长知识。只有将数学学科知识与学生生活体验进行关联，学生所掌握的数学知识才能变得灵动而有张力。为此，教师应带领学生走进数学问题的真实情境，寻求解决数学问题的方法，形成数学关键能力和必备品格。而在实际的数学课堂教学中，有些教师往往过于强调学习内容的知识性，忽略了知识应用的实践性，出现许多脱离学生生活实际与活动体验的低效教学。学生也在这样的教学中逐渐失去对数学学习的兴趣与动力，从而出现“坐而论道，纸上谈兵”的教学现象。

二、发掘需“联”求“变”的内涵价值

关联是整体性的重要特征，变化是整体性的表现形式。有了关联，整体包含的各个部分或要素才会组成相互联系的有机整体；有了变化，整体也就表现出各个部分或要素个体特性之和以外的整体特性。整体性观照下的数学教学离不开关联与变化，教师需要发掘出数学教学中原本隐含的关联与变化，才能凸显数学整体性教学的价值。结合数学课程的实施，需“联”求“变”不仅是数学课程内容实施的客观需要，还是学生构建完备数学认知的重要途径，更是学生锻炼并获得数学核心素养的重要保障。

（一）是数学课程内容体系的建构方式

义务教育阶段数学课程内容编排以学段为单位，课程内容相互关联，逐段递变，螺旋上升，构成相对系统的知识结构。课标强调，为实现核心素养导向的教学目标，不仅要整体把握教学内容之间的关联，还要把握教学内容主线与相应核心素养发展之间的关联。可见，关联及其催生的变化是课标实施的重要理念。

（二）是数学有效课堂教学的重要抓手

有效的数学课堂教学需要教师在数学知识的关联中，把握内容贯穿的主线，找准学习起点，厘清数学学习脉络，促进学生沿着内容主线整体性地学。有效的数学课堂教学还需要教师在诸多教学要素的关联中，把握内容的主次地位，凸显核心知识，帮助学生根据内容的重要性由主及次整合地学。

（三）是数学核心素养落地的务实行动

数学核心素养是学生在数学学习过程中逐渐形成的，是他们面向未来社会和个人发展所必备的重要素养。在教学中，教师不仅要重视数学知识体系内部的关联，还要重视数学与其他学科知识之间、数学与科学技术和社会生活之间的关联，在丰富而灵动的关联中，让学生理解“万变不离其宗”的数学规律及其包含的基本数学思想，学会用数学的眼光观察、用数学的思维思考、用数学的语言表达现实世界，从而形成和发展学生的数学核心素养。

三、实施从“联”向“变”的有效策略

（一）上下关联，变短为长

数学知识的产生与来源、发展与变化、综合与应用等具有联系紧密的内在结构，有效的数学课程实施需要顺应数学知识的内在发展脉络进行上下关联，在内容上连接知识“点”，形成结构“链”，变“短聚焦”为“长视程”，帮助学生用整体的、联系的、发展的眼光研究数学现象，促进学生对数学知识体系的整体性建构与全方位认知。

例如，教学“三角形的高”时，在学生初步掌握三角形高的概念后，教师展开如下探究：

1.“三角形的高”与“直线外一点到这条直线距离”相联系

课件先隐去三角形中与这条高无关的两条边，保留一组相对的顶点、底及高（如图1），让学生将其与以前学习的“直线外一点到直线的距离”（如图2）进行比较。

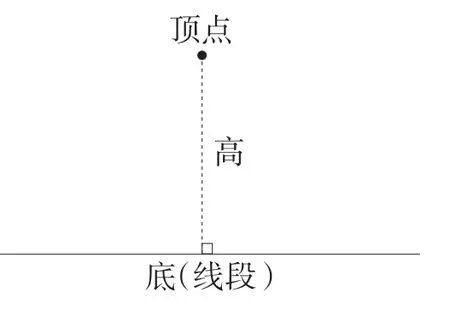
图1

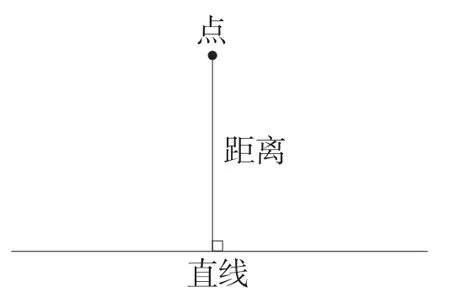
图2

2.“三角形的高”与“两条平行线之间的垂直线段”相联系

在钉子板上平移三角形的这个顶点，围出不同的三角形，让学生找出它们的高（如图3），比较并思考为什么这些三角形高的长度相等。

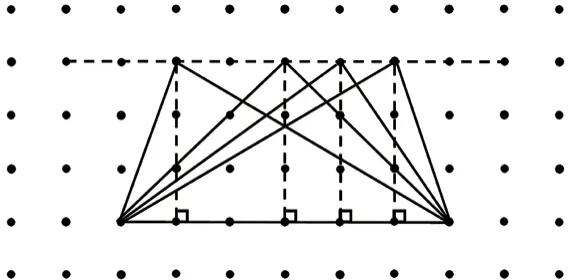
图3

3.“三角形的高”与“锐角三角形、直角三角形、钝角三角形”相联系

在钉子板上把这个顶点继续向一边平移，得到直角三角形、钝角三角形（如图4），研究并理解这三种不同类型三角形的高所具有的共同特质。

图4

（二）左右关联，变小为大

郑毓信教授指出，整体性教学“应当超出单独的每一节课、每一具体的学习内容并从更大范围进行分析与思考”。教师要从分散在不同单元板块、不同类型的数学知识中，整合具有内在关联的内容进行学习，体现数学知识的左右横向关联，放大数学探究视域，在复杂数学知识中探索共性规律，形成简约认知，从而减轻学生的学习负担，提升他们的数学学习成效。

例如，在教学“乘法分配律”时，教师通过画点子图、长方形面积计算、竖式计算等形式，让学生充分理解乘法分配律的要义。

（1）出示问题：光明小学四年级有10个班，五年级有8个班，每个班领24个篮球，四、五年级一共要领多少个篮球？

（2）用点子图直观表示四、五年级

（三）内外关联，变静为动

学生学习数学需要强化内部的数学知识与外部的其他学科知识、科学技术和社会生活之间的联系，在实际情境和真实问题中，经历发现问题、提出问题、分析问题、解决问题的过程，积累活动经验，变静态的数学知识为灵动的思想方法，促进核心素养的形成和发展。

例如，在学习“折线统计图”这一单元时，教师设计“身高增长的秘密”主题活动，让学生运用折线统计图的相关知识研究少年儿童身高增长的规律。

（1）收集整理自己一年级入学以来逐年体检的身高数据，绘制自己一到五年级身高增长变化情况的单式折线统计图，研究了解哪一阶段身高增长得较快，哪一阶段身高增长得较慢。

（2）根据《中国儿童身高管理现状调研报告》提供的标准身高数据，选择与自己同性别的标准身高数据，绘制自己一到五年级以来身高增长与同性别标准身高变化进行对比的复式折线统计图，研究自己的身高与同性别标准的身高比较情况。

（3）绘制3～15周岁男生和女生标准身高变化情况的复式折线统计图，研究了解不同性别少年儿童身高增长的普遍规律。

（4）将自己的身高增长变化与其他同性别学生进行比较，研究了解促进身高增长的因素，科学制订计划。

实践证明，从“联”向“变”不仅充分体现了数学教学的整体特质，还是形成和发展学生数学核心素养的有效教学策略，在学生综合素质的全面提升中发挥着重要作用。