基于多层特征融合注意力网络的电能质量扰动识别方法
2022-10-30奚鑫泽邢超覃日升刘辉周鑫和鹏孟贤
奚鑫泽,邢超,覃日升,刘辉,周鑫,和鹏,孟贤
(1.云南电网有限责任公司电力科学研究院,云南昆明 650217;2.广西大学,电气工程学院,广西南宁 530004)
0 引言
随着泛在电力物联网的快速发展,分布式能源与非线性负载集成到电网中,如大量的固态开关设备、电力电子开关、非线性负载等接入容易导致电网的电压、电流畸变严重,电能质量问题严峻,甚至已经对电网设备的稳定运行造成影响[1-3]。因此,对电能质量扰动类型进行精准辨识是电能质量优化控制的关键[4]。
当前电网环境复杂,各类新能源的并网造成电压信号严重畸变,电能质量扰动(Power Quality Disturbance,PQD)识别技术亟需开展深入研究。准确识别PQD,需提前获取PQD 的扰动特征,近年来,很多时频分析的方法被用在PQD 领域[5-8]。文献[9-10]将小波分解应用在电能质量扰动特征提取上,但小波基难以准确选取,影响扰动识别的准确性。文献[11-12]将稀疏分解应用在电能质量扰动参数检测上,但稀疏字典的构造缺乏自适应性。文献[13-14]通过S 变换构造PQD 信号的时频矩阵,进而构造PQD 的时域与频域特征进行扰动辨识,但S 变换中窗参数的选取缺乏理论依据,难以获取最佳时频分辨率,影响扰动识别精度。
现有的时频分析方法难以自适应获取PQD 特征。近年来,大数据、深度学习等理论的发展使得大规模并行处理电能质量数据并自适应提取扰动特征成为可能。文献[15]通过循环神经网络获取电能质量扰动信号的时序特征,进而进行PQD 识别,但对于暂态扰动特征提取精度不高。文献[16]提出一种格拉姆角场变换与卷积神经网络(Convolutional Neural Network,CNN)相结合的电能质量扰动分类方法,但文中将电能质量扰动转为二维图像进行识别,失去扰动信号的物理意义。文献[17]将长短时记忆网络(Long Short-Term Memory,LSTM)融合CNN 进行PQD 识别,但网络结构复杂,训练时间长,容易过拟合。
为弥补现有方法在复杂电网环境下对电能质量扰动分类的不足,本文通过多层卷积神经网络逐层提取电能质量扰动信号的高维特征,引入注意力机制增强模型对扰动信号局部特征与全局特征的有效融合,提升各PQD 关键特征信息关注度,提高扰动特征识别度,利用softmax 函数对PQD 进行分类,据此提出基于多层特征融合注意力网络的电能质量扰动识别方法,并经仿真实验验证了该方法的准确性与适用性。
1 多层特征融合注意力网络
1.1 卷积神经网络
CNN 是一种典型的前馈神经网络,通过一系列交替设置的卷积层和池化层自适应提取特征,进而通过分类器进行分类[18]。用于分类任务的CNN 典型网络结构如图1 所示。

图1 卷积神经网络模型一般结构Fig.1 Architecture of CNN model
本文对PQD 信号进行分类,本质上处理的是时间序列,故采用一维卷积神经网络。对于输入维度为n的离散时间序列Xn=[x1,x2,…,xn],一维卷积层的映射过程可表示为:

式中:xi+j-1为输入的第i+j-1 的特征值;s为卷积核的大小;kj为第j个卷积核中神经元的权重;b为偏置;f(*)为非线性激活函数;yi为第i个卷积的输出值(i取值范围是[0,n-s+1],即卷积的输出是长度为n-s+1 的序列)。
式(1)中的非线性激活函数f(*)取Relu 函数,相比Sigmoid 函数有防止梯度弥散和计算速度快等优点,其表达式为:

式中:x为输入的特征值。
卷积神经网络通过池化操作将池化区域内的一系列数据按一定规则转化为一个输出值,有效减少了模型的参数,提升了模型的运算速度。通常有式(3)的均值池化hmean与式(4)的最大池化hmax。

式中:ℕ 为池化域内的所有序列数据组成的集合;N为待池化区域的特征值数量;max(*)表达式为输出集合中的最大值。
通过卷积池化操作后构造的特征向量经过全连接层映射进行分类,其映射可表示为:

式中:W为权重矩阵。
1.2 注意力机制
由于不同扰动信号的特征不同,因此在识别不同类别扰动时,各层特征的重要性也不同。为了表征各个特征层的重要程度,进而根据特征本身的特点加强重要特征并抑制不重要的特征[19],本文采用压缩-拓展模块的注意力机制实现多层特征的融合,其基本结构如图2 所示。

图2 压缩-拓展注意力模块Fig.2 Squeeze-and-excitation attention block
图2中L为特征图的通道数,F为每个特征向量的维度,r为压缩系数。对于输入尺寸为L*F的特征图,首先采用全局池化得到1*L的压缩向量,以获得卷积特征图的每个通道的全局信息嵌入(特征向量)。由于每个通道只有一个特征值,得到的特征向量具有全局性。然后采用两层全连接层进行压缩拓展变换,此时得到了1*L的注意力系数向量,以表征不同层特征的重要性。该结构灵活简单,添加后网络的训练速度不会大幅降低。各通道之间的关系是相互独立的,因此学习到的注意力系数能够激励重要的特征,抑制不重要的特征,在深度网络中起到特征选择的作用,有效提高扰动识别精度。
1.3 多层特征融合注意力网络构建
为提升各PQD 关键特征信息关注度,提升电能质量扰动的辨识精度,构建了注意力机制融合多层CNN 输出特征,提出一种多层特征融合注意力网络(Multi-layer Feature Fusion Attention Network,MLFFAN),整个网络模型框架如图3 所示。

图3 MLFFAN算法框图Fig.3 Flow chart of MLFFAN algorithm
如图3 所示,该网络主要由CNN、特征注意力以及分类器等3 个模块构成。其中,CNN 模块由4个堆叠的卷积块构成,卷积块结构如图4 所示。

图4 卷积块结构Fig.4 Structure of convolution block
从图4 可以看到,每个卷积块包括1 个卷积层、1 个激活层和1 个池化层。每个卷积层的卷积步长设置为1,网络逐层获取PQD 局部特征,并最终提取PQD 全局特征;每层卷积后面采用Relu 激活函数进行非线性变换;最后,采用最大值池化降低特征维度,筛选重要特征。对于给定长度为n的扰动信号xn,每个卷积块的映射过程可以表示为:

式中:fRelu(*)为Relu 激活函数;m为最大值池化的核大小;Fi为卷积块的第i个输出。最终,4 个卷积层分别得到4 个特征向量F1,F2,F3和F4。
得到4 个特征向量之后,采用1.2 节所述的压缩-拓展模块计算各个特征向量的注意力系数,进行特征融合。
由于网络的逐层递增,PQD 局部特征容易丢失,并造成特征冗余。因此,通过注意力机制融合网络输出的PQD 特征,提升网络对关键扰动特征的关注度,各特征层与相应的注意力系数相乘构建PQD 特征向量,消除特征冗余,提高PQD 识别准确性。
在进行特征融合之前,首先通过全局均值池化操作对各个卷积块输出的特征(F1,F2,F3,F4)进行降维,得到特征向量,降维过程为:

式中:fGAP(*)为全局均值池化。
然后,采用式(9)计算注意力系数αi。

式中:σ为Sigmoid 激活函数;W1为2*4 维度的压缩矩阵;W2为维度为4*2 的拓展矩阵;δ为Relu 激活函数;fMax(*)为全局最大值池化。
然后,将各个特征向量与相应的注意力系数相乘并拼接,得到最终融合的特征向量Fz,具体融合过程如下:

最后,采用单隐藏层的全连接神经网络直接对融合特征进行变换,通过Softmax 函数得到最终扰动类别标签。
模型训练过程中以交叉熵损失为损失函数Loss进行迭代优化,表达式为:

式中:N为样本数量;K为类别数量;yi,k和pi,k分别为第i个样本的第k个标签的真实值和预测值。
构建的多层特征融合注意力网络MLFFAN 的电能质量扰动识别方法的参数(无量纲)设置如表1所示。

表1 MLFFAN模型参数设置Table 1 Setting of MLFFAN model parameters
2 实验结果与分析
2.1 扰动信号仿真数据集
根据PQD 的IEEE Std.1159 标准,基于暂升、暂降、中断、闪变、谐波、脉冲暂态和振荡暂态7 种典型的单一扰动信号建立18 种单一和复合扰动的数学模型,具体类别与标签见表2。

表2 扰动类别及其标签Table 2 PQD types and labels
在MATLAB 生成PQD 数据集,扰动模型中涉及到的变化参数,如扰动幅值、扰动开始时刻、扰动结束时间、谐波频率、振荡幅值、振荡频率相对系数等,通过取其参数范围内的随机数的方式确定(随机数选取呈现均匀分布)。本文设置基频为50 Hz,采样频率为一般录波设备的采样频率3.2 kHz,采样10 个周期,共640 个采样点。单一扰动的仿真波形如图5 所示,其横坐标为采样点序号。

图5 单一扰动的仿真波形Fig.5 Simulated waveforms of single PQD
每种扰动类型生成500 个样本,随机选取其中300 个作为训练集,100 个作为验证集,100 个作为测试集。最终,得到5 400 个训练样本、1 800 个验证样本和1 800 个测试样本。考虑实际环境中的噪声问题,在扰动数据集上添加高斯白噪声,信噪比为20~50 db 之间的随机值。此外,为了全面评估模型抗噪性,本文额外构造信噪比分别为20 db,30 db,40 db,50 db 的测试集。
2.2 仿真结果与分析
为了更加直观地说明所提特征融合网络对特征区分度的影响,通过t分布随机领域嵌入(t-Distributed Stochastic Neighbor Embedding,t-SNE)降维可视化方法,将8 种单一扰动(C0-C7)的原始数据和网络提取的特征降成二维并可视化,如图6 所示,横纵坐标表示二维特征空间的2 个维度(无量纲)。
图6(a)是对原始扰动数据的可视化结果,在特征提取之前,8 种单一扰动的可分性较差,只有部分扰动类型如C01 谐波和C05 暂升相对可分,聚为一簇。图6(b)是经过所提特征融合网络提取特征后的可视化结果,每种单一扰动基本聚为一簇,且不同扰动类别直接相隔一定距离,说明特征的可区分度很高,易于分类。

图6 t-SNE特征可视化Fig.6 Feature visualization with t-SNE
在Pytorch 实现本文所提多层特征融合注意力网络的电能质量扰动识别方法,网络的最小批尺寸设为128,共迭代训练50 次,训练过程如图7 所示。

图7 训练过程的正确率和交叉熵损失Fig.7 Accuracy and cross entropy loss in training process
从图7 可知,随着模型训练次数的递增,训练集和验证集的正确率逐渐提升,损失也随之下降。当训练迭代次数达到30 次之后,训练集与验证集的正确率、损失基本不再变化,验证集扰动识别正确率与训练集扰动识别正确率基本相同,表明此时模型收敛,并具有很强泛化能力。
为验证本文所提算法的适用性,采用各类复合扰动及混合扰动的测试集对模型进行测试,仿真结果如表3 所示,其中“综合”表示采用包含所有扰动类别的测试集的测试结果。

表3 MLFFAN方法的扰动分类效果Table 3 Disturbance classification result of MLFFAN method %
从表3 可以看到,本文所提的MLFFAN 分类方法可有效对各种噪声条件下多重复合扰动精准分类,在信噪比为20 dB 的极端噪声环境下模型的分类正确率扔可达95%,可见模型具有较高抗噪性能。在随机噪声下,模型对单一扰动和二重扰动的分类正确率接近100%,对三重复合扰动也有约98%的正确率。综合来看,MLFFAN 方法在20~50 db的随机噪声下识别本文所述18 种扰动的整体正确率可达99.22%,可见模型具有较高的分类正确率。
为了进一步说明所提MLFFAN 模型的有效性,构建了3 种其他的深度模型作为对比,对比模型的结构说明如下:
1)CNN:在所提MLFFAN 模型的基础上,去掉网络的中间层输出和注意力融合模块,仅保留经典的卷积分类网络的结构;
2)CNN-LSTM[20]:先采用CNN 提取出扰动信号的深层特征序列,再用LSTM 捕捉特征序列的时序相关性,最后对输出特征进行映射分类。网络的结构与参数均选择文献[20]提出的最优参数;
3)Deep-CNN[17]:一种由一维卷积层、批归一化层和池化层堆叠而成的6 层深度卷积网络。各层卷积的卷积核数量分别设为32,32,64,64,128 和128。网络的结构与其他参数均选择文献[21]提出的最优参数。
采用Pytorch 框架实现上述3 种对比模型,设置迭代轮次为50 次,在相同配置环境下对4 种算法进行扰动分类实验,结果对比如表4 所示。

表4 4种算法的结果对比Table 4 Results comparison of 4 calculation methods%
从表4 可知,所提MLFFAN 在各种噪声水平下均取得了最高的分类正确率。相比于传统的CNN网络,MLFFAN 的正确率提高了约1%,表明本文通过注意力机制融合多层特征层,有效改进了CNN 算法性能,提升了PQD 分类正确率。
为了进一步验证所提MLFFAN 模型对复合扰动细节特征的提取能力,测试了不同深度模型在20~50 dB 随机噪声条件下对各类扰动的识别情况。由表4 可知,Deep-CNN 模型在不同对比模型中识别精度表现最好,因此选择Deep-CNN 与MLFFAN进行对比分析,具体结果如图8 所示。

图8 不同扰动类型的识别情况Fig.8 Identification of different PQDs
如图8 所示,2 个模型对C8,C9,C10,C15,C16和C17 这6 种扰动类别的识别精度有明显降低。相比于Deep-CNN 模型,本文所提MLFFAN 模型对这6 种扰动类型的识别精度有较大提升。C8,C9,C10 分别表示振荡暂态和暂升、暂降以及中断的组合,C15,C16 和C17 是在C8,C9,C10 基础上叠加了谐波。为了便于分析,将C8 谐波+暂升和C15 谐波+振荡暂态+暂升的扰动波形(信噪比为30 dB)绘制在图9,其横坐标为采样点序号。
如图9 所示,由于暂升和谐波这2 种扰动的幅值特征和频率特征变化明显,而振荡暂态的扰动发生时间短、振荡幅度小,导致此类型扰动更加难以识别,进而导致C8 和C15 2 种扰动类型的混淆。同理,C9 和C16 之间、C10 和C17 之间也会产生同样的混淆问题。但实验结果表明,本文所提MLFFAN 模型在这6 种难识别扰动的分类精度上有较大提升,这是由于所提方法融合卷积网络各层的特征数据,能够同时有效提取扰动信号中的细节特征和全局特征,相比于其他深度学习算法有效减少了细节特征的丢失,保留原扰动信号中的细节信息。
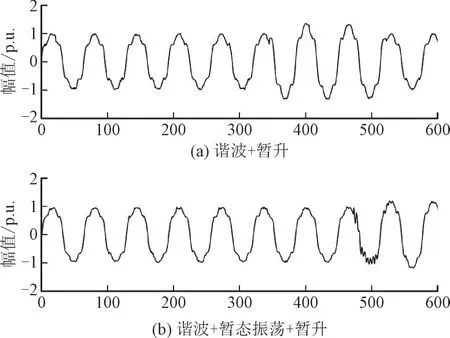
图9 C8和C15的扰动波形Fig.9 Waveforms of PQD C8 and C15
最后,将本文所提MLFFAN 算法与现有的扰动识别算法进行对比,进一步分析MLFFAN 方法的优越性。3 种传统方法分别是采用离散小波变换(DWT)和概率神经网络的方法(DWT+PNN)[21]、采用变分模态分解和决策树的方法(VMD+DT)[22]以及采用可调品质因子小波变换和随机森林的方法(TQWT+RF)[23]。另外,将文献[24]采用的相空间重构和卷积神经网络方法(PSR+CNN)、文献[25]采用的稀疏自编码器方法(SSAE)2 种深度学习方法与本文方法在同一环境下进行扰动分类实验对比。比较结果如表5 所示。

表5 本文所提方法与现有方法的对比Table 5 Comparison between proposed method and existing methodss %
由表5 可知,整体上自动提取特征的扰动分类方法在各个噪声水平下识别精度高于人工提取特征的传统方法。相较于传统PQD 分类方法,所述MLFFAN 方法通过多层卷积池化后,并引入注意力机制,融合各层扰动特征,自适应构造扰动特征向量作为最后全连接层的输入,避免传统方法中的人工特征选取的问题,也解决了人工选取特征往往仅针对特定扰动识别效果好,限制模型的扰动识别数量的问题。相比于现有的深度学习方法,所述MLFFAN 方法优于文献[24]采用的相空间重构和卷积神经网络方法。文献[25]提出的稀疏自编码器方法虽然略高于MLFFAN 方法,但其仅能识别9 种扰动,难以处理实际中的复杂扰动情形,因此本文所提的MLFFAN 更适用于PQD 分类。
3 结论
为实现复杂电网环境下电能质量扰动特征自适应提取,提高扰动识别正确率,提出了基于多特征融合注意力网络的电能质量扰动识别方法。特征可视化的结果表明,所提特征融合注意力网络能够提取有效特征,增加扰动类别之间的区分度;仿真结果表明:通过低维到高维的多层特征融合改进了传统卷积神经网络的特征提取过程,提升了电能质量扰动特征辨识度;特征注意力机制提升了网络对电能质量扰动信号全局特征与局部特征的关注度,提高模型泛化能力。本文所提方法在单一扰动、复合扰动与噪声环境下均能有效对电能质量扰动进行识别,与主流检测方法相比,本文所提方法能够有效构建复杂电网环境下电能质量扰动信号的全局特征与局部特征,减轻了传统卷积神经网络的过拟合问题,促进了卷积神经网络在复杂电网环境下电能质量扰动识别的应用。
