弱电网不对称故障下正负序电流控制耦合作用对DFIG稳定性影响分析

2022-10-30王凌云王红兵黄云辉王栋熊斌宇周克亮

智慧电力 2022年10期

王凌云，王红兵，黄云辉，王栋，熊斌宇，周克亮

（1.武汉理工大学自动化学院，湖北武汉 430070；2.国网湖北黄石供电公司，湖北黄石 435000）

0 引言

随着风电渗透率的提高，各国纷纷开始制定更加严格的“风力发电系统低电压穿越并网准则”以保障电力系统的稳定性[1-5]。我国在并网标准中明确指出在电网故障期间，风机应根据端电压的变化向电网注入相应的无功电流以支撑电网电压[1]。双馈风机（Doubly Fed Induction Generators，DFIG）以其可变速恒频运行、变频器容量低且成本小等优点在风力发电系统中得到广泛的应用[6-10]。受自然资源的地理分布影响，我国部分风电基地远离负荷中心，其风电机组在弱电网条件下输出的电流波动较大，对并网点电压造成巨大影响，导致风机稳定性不足[11-15]。另外，电网电压故障也会影响并网点电压的稳定性，进一步加剧风机失稳的风险[16]。因此，电网电压故障下连接弱电网的DFIG 稳定性问题亟待解决。

近年来，研究人员针对弱电网对称故障下DFIG稳定性进行了广泛研究。文献[17-18]分析对称故障下影响DFIG 稳定性的因素，包括短路比（Short Gircuit Ratio，SCR）、电压跌落深度、锁相环和转子电流环的控制参数，得出在弱电网条件下应设置更慢的锁相环带宽和更快的转子电流环带宽的结论。文献[19]建立考虑网侧电流控制回路的小信号状态空间模型，分析转子转速对DFIG 稳定性的影响，研究发现转子转速越快、系统稳定性越差。文献[20-21]建立DFIG 系统下小信号阻抗模型，采用奈奎斯特稳定判据分析了低电压穿越过程中DFIG 系统的稳定性。文献[22]采用复转矩系数法，使用总恢复系数和总阻尼系数对锁相环和转子电流环控制参数的作用进行了定性和量化。研究发现：锁相环带宽越高，系统的总阻尼系数越低，系统稳定性越差；转子电流环带宽越高，系统总阻尼系数越高，系统稳定性越好。文献[17-22]研究的缺点在于忽略了不对称故障的情况和负序控制系统对风机稳定性的影响。

目前，学者们针对不对称故障下的研究多集中于控制策略，对于稳定性机理的研究较少[23-28]。文献[27]采用间接功率控制，制定DFIG 不对称故障下的控制策略，抑制了故障期间风机有功功率和无功功率的脉动。文献[28]根据不对称故障下最小相电压与正序电压和最大相电压与负序电压的关系，提出一种不对称故障下正负序电流注入方法，以达到支撑电网电压的目的。文献[27-28]将不对称故障下的设备划分为正序设备和负序设备并单独分析其影响，忽略了正负序分量耦合作用的影响。文献[29]分析不对称故障下复杂电网序分量之间的耦合关系，但没有考虑正负序分量耦合作用对发电机的影响。文献[30]分析正负序d轴电流对锁相环的影响，发现合理设置正负序电流可使锁相环阻尼比增大、系统稳定性增强，并提出一种考虑电流容量限制的自适应最优电流控制算法，但未考虑正负序电流控制耦合作用对系统的影响。由文献[27-30]可知，针对弱电网不对称故障下正负序电流控制的耦合作用对DFIG 稳定性的影响机理分析还处于空白阶段，亟需开展研究。

综上所述，本文针对弱电网不对称故障下DFIG正负序电流控制耦合作用对DFIG 稳定性的影响机理尚不清晰的问题，提出一种分析正负序电流控制耦合作用影响机理的方法。研究的创新之处在于：（1）建立了弱电网不对称故障持续阶段考虑正负序电流控制耦合动态的DFIG 小信号模型；（2）揭示了弱电网不对称故障下DFIG 正负序控制环路之间的耦合作用对系统稳定性的影响机理。

1 DFIG和不对称故障网络小信号建模

1.1 DFIG小信号模型

为分析不对称故障下连接弱电网的DFIG 正负序电流控制耦合特性，考虑DFIG 各电流控制环路动态、电网强度和运行点等因素，建立不对称故障下连接弱电网的DFIG 小信号模型。模型定义如下：（1）正负序分离环节分离完全；（2）定子电流流出绕组为正方向，转子电流流出绕组为正方向；（3）不考虑前馈项的影响。

根据稳态下DFIG 机侧变流器和网侧变流器的电路关系，可得正序机侧变流器与网侧变流器的小信号公式为：

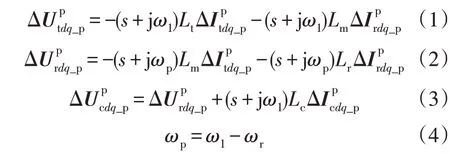
由于负序机侧变流器与网侧变流器的电路关系与正序部分仅在电网同步转速上相反，故负序机侧变流器与网侧变流器的小信号公式为：

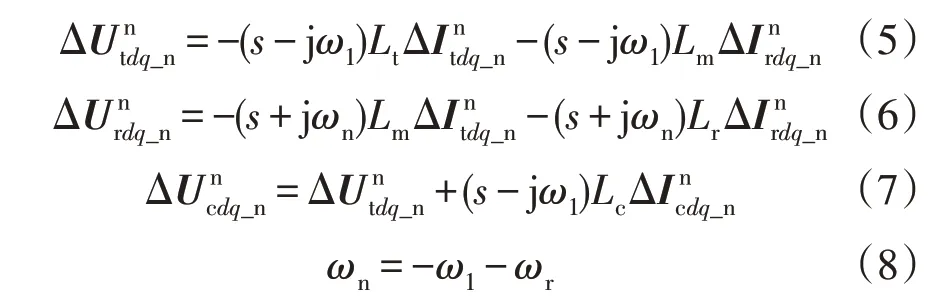
由于电流控制器需要锁相环得到的相位作为控制输出电流的依据，故在描述电流控制器动态时首先考虑锁相环动态的影响。本文所建模型采用正负序双锁相环控制，正负序锁相环的小信号公式为：

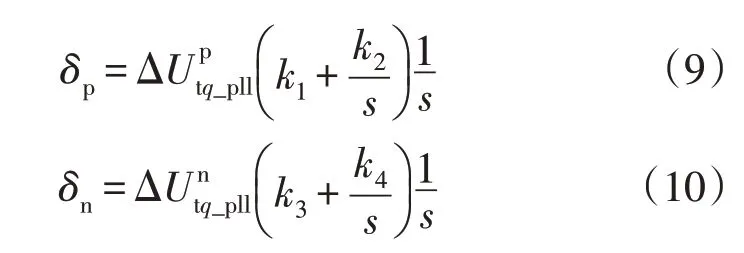
式中：δp，δn分别为正序锁相环相位差和负序锁相环相位差；分别为正序锁相环坐标系下正序q轴定子电压的小信号矢量、负序锁相环坐标系下负序q轴定子电压的小信号矢量；k1，k2均为正序锁相环PI 参数；k3，k4均为负序锁相环PI 参数。

获得正负序锁相环小信号公式后，机侧电流环小信号公式为：

1.2 不对称故障网络小信号模型

根据式（1）—式（13）可建立不对称故障下DFIG小信号模型，但在弱电网条件下并网点电压受DFIG输出电流影响较大，且不对称故障中电网正负序分量之间存在耦合。故建立考虑DFIG 正负序电流控制耦合作用的小信号模型，还需要建立不对称故障网络的小信号模型。不对称故障网络电路图如图1 所示。图1 中，Ug，Ut，It分别为矩阵形式下的无穷大电网电压、定子电压、定子电流，Z1为近风端阻抗，Z2为远风端阻抗，Zf为短路阻抗，Ifa，Ifb分别为a，b 相短路电流，IEa，IEb，IEc为流入电网的a，b，c 三相电流，Ita，Itb，Itc为风机定子a，b，c 三相电流。

由图1 可得，αβ坐标系下矩阵形式的不对称故障网络公式为：

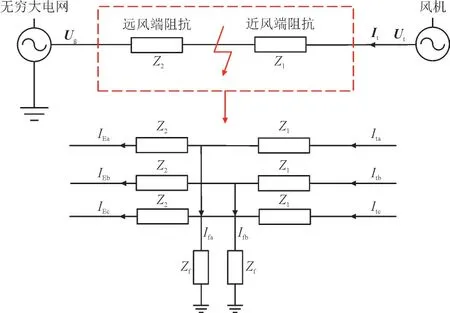
图1 不对称故障网络电路图Fig.1 Circuit diagram of power grid under asymmetric fault

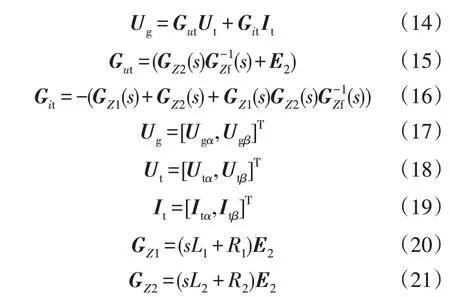
式中：Gut，Git分别为定子电压到无穷大电网电压的矩阵传递函数、定子电流到无穷大电网电流的矩阵传递函数；GZ1，GZ2，GZf分别为近风机端阻抗矩阵传递函数、远风机端阻抗矩阵传递函数、短路阻抗矩阵传递函数；Ugα，Ugβ分别为无穷大电网电压在α轴和β轴上矢量分量；Utα，Utβ分别为定子电压在α轴和β轴上矢量分量；Itα，Itβ分别为定子电流在α轴和β轴上矢量分量；L1，R1，L2，R2分别是近风端阻抗电感、电阻和远风端阻抗电感、电阻；E2为二阶单位矩阵。

由于短路阻抗矩阵传递函数三相不平衡，函数GZf表达式为：

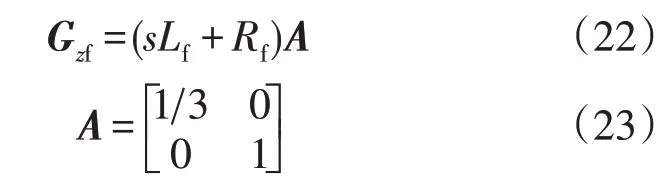
式中：Lf，Rf分别为短路阻抗电感和短路阻抗电阻；A为两相接地短路故障矩阵。

由文献[20]可知，若在αβ坐标系下电压电流有如下矩阵关系：

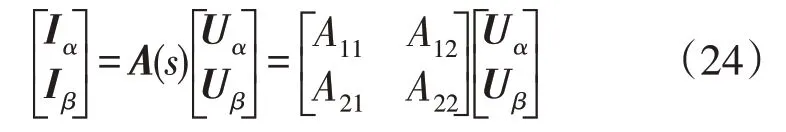
式中：Iα，Iβ为电流矢量在α轴和β轴上分量；Uα，Uβ为电压矢量在α轴和β轴上分量。A11，A12，A21，A22分别为矩阵A的第1，2，3，4 个元素。

在矢量关系式形式下电压电流关系可写为：

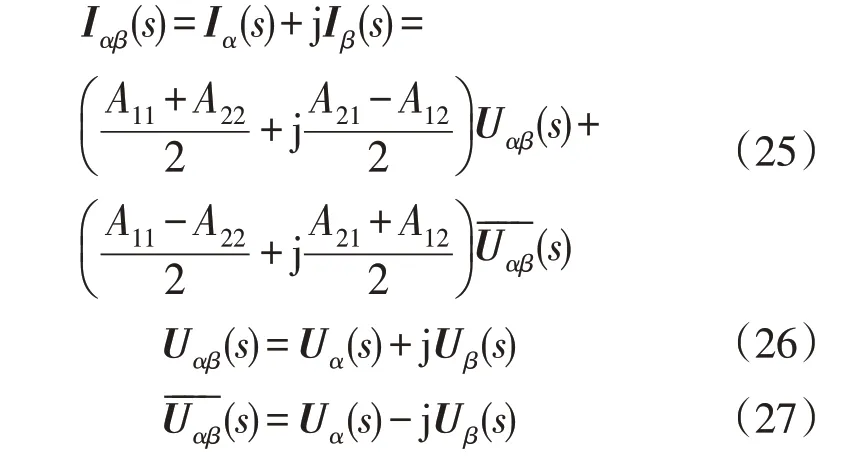
式中：Iαβ(s)为复频率形式下的电流矢量；Iα(s)，Iβ(s)分别为复频率形式下电流在α轴和β轴上矢量分量；Uαβ(s)为复频率形式下的电压矢量；为Uαβ(s)的共轭；Uα(s)，Uβ(s)分别为复频率形式下电压在α轴和β轴上矢量分量。

由式（25）可知，电网中受任意复频率电压矢量激励产生的电流矢量可写成2 种复频率矢量的和。这2 种复频率一种和电压矢量相同，一种与电压矢量共轭。由于在对称故障网络或正常电网中A11与A22相同、A21与A12均为0，故在对称故障网络和正常电网中不存在正负序耦合现象。而在不对称故障网络中，由于三相不平衡的特性导致A11与A22不同，从而导致不对称故障电网中存在正负序耦合现象。

由式（14）—式（25）可得线性化后两相旋转坐标系下端电压与端电流的关系为：

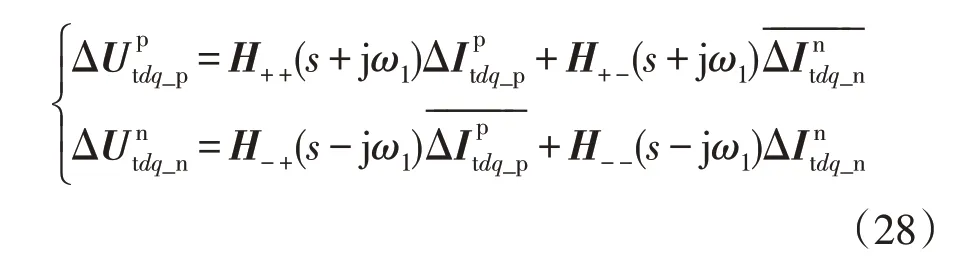
根据式（1）—式（28）可得不对称故障下考虑正负序电流耦合控制作用的DFIG 小信号模型如图2 所示。图2 中，j 为虚部运算，Conj 为共轭运算，PI 为PI 控制器，传递函数G1（s）—G8（s）由DFIG 控制参数、电网强度和故障深度共同决定。由图2 可知，不对称故障使得故障电网中正负序分量存在耦合，进而导致双馈风机正负序电流控制器之间存在相互作用；弱电网条件下双馈风机对端电压的影响被放大，加剧了正负序电流控制器的耦合作用。

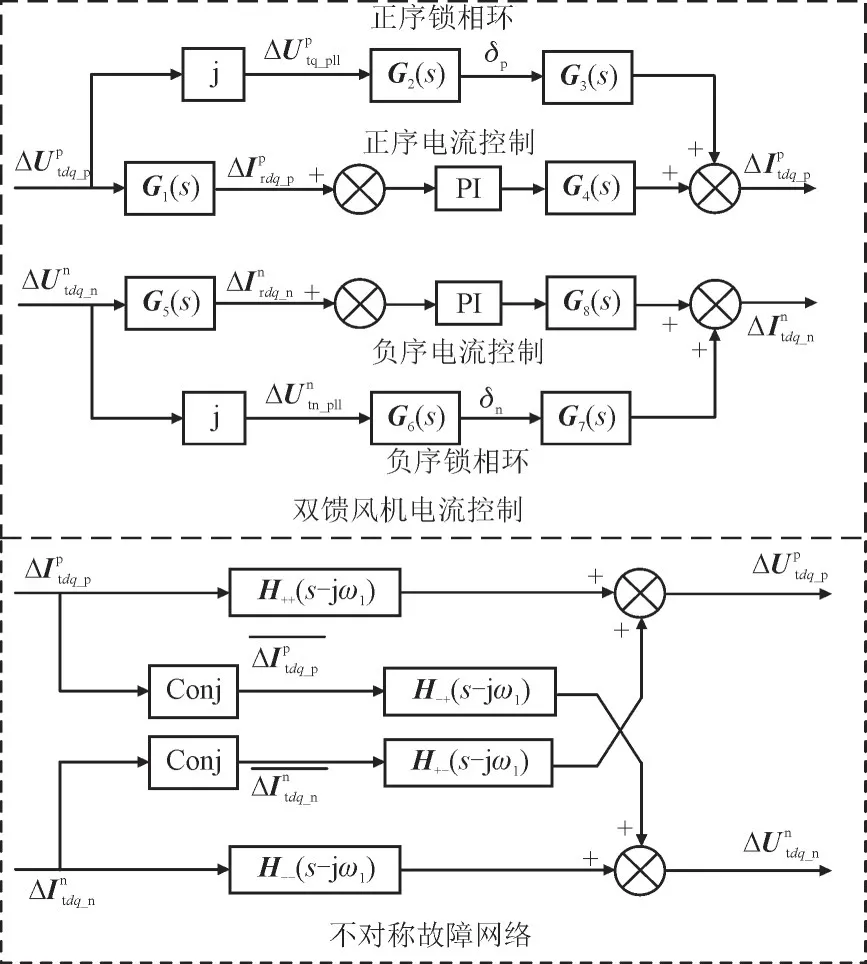
图2 不对称故障下考虑正负序电流耦合控制作用的DFIG小信号模型Fig.2 Small signal model of DFIG considering coupling effect of positive and negative sequence current control under asymmetric fault

2 DFIG稳定性分析

2.1 不同物理条件对DFIG稳定性影响

根据不对称故障下考虑正负序电流耦合控制作用的DFIG 小信号模型，分析电网参数和DFIG 控制参数对风机稳定性的影响。电网参数包括电网强度和电压跌落深度，DFIG 控制参数包括正序电流环带宽和负序电流环带宽。DFIG 控制参数和电网参数如表1 所示。

表1 DFIG控制参数和电网参数Table 1 DFIG control parameters and main circuit parameters

不对称故障下电网参数和DFIG 控制参数对风机稳定性的影响如图3 所示。

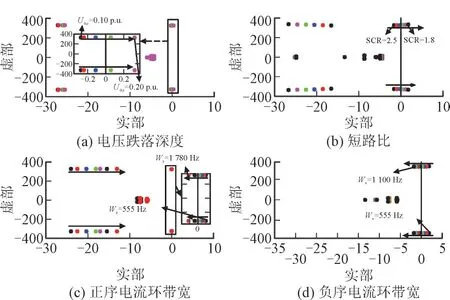
图3 不对称故障下电网参数和DFIG控制参数对风机稳定性的影响Fig.3 Influence of power grid parameters and DFIG control parameters on DFIG stability under asymmetric fault

图3 中，实线箭头表示特征根移动趋势，虚线箭头指代放大区域，Udip为电压跌落深度，Wp，Wn分别为正序电流环带宽和负序电流环带宽。

由图3 可知，图3（a）中电压跌落深度从0.1 p.u.逐渐增大致0.2 p.u.，系统主导特征根右移，逐步失去稳定，说明越严重的不对称故障越容易使DFIG失去稳定；图3（b）中短路比从2.5 下降至1.8，系统主导特征根右移，逐渐失去稳定，说明不对称故障下电网强度越弱系统越不稳定；图3（c）中正序电流环带宽从555 Hz 上升至1 780 Hz，系统主导特征根左移，系统从不稳定变为稳定，说明不对称故障下增大正序电流环带宽有利于系统稳定；图3（d）中负序电流环带宽从555 Hz 上升至1 100 Hz，系统主导特征根左移，系统从不稳定变为稳定，说明不对称故障下增大负序电流环带宽有利于系统稳定。

2.2 正负序电流控制耦合作用对DFIG稳定性影响

以正序电流控制为例，不对称故障下DFIG 正负序耦合作用机理如图4 所示。

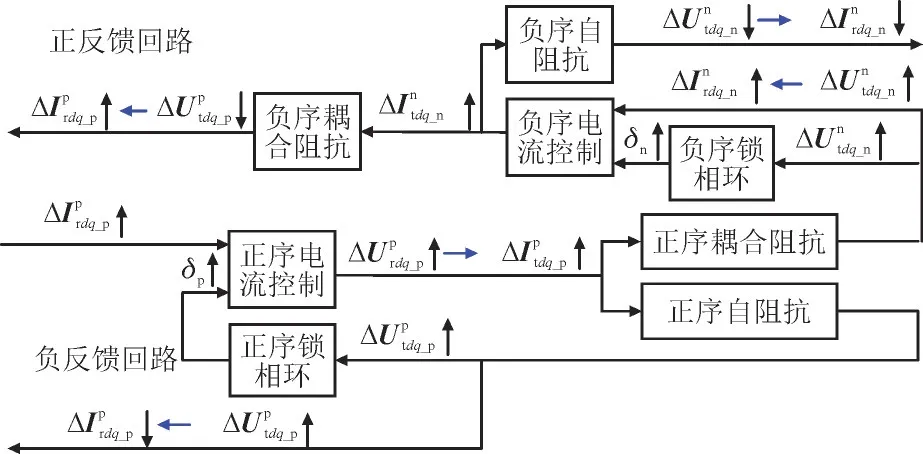
图4 不对称故障下DFIG正负序耦合作用机理Fig.4 Coupling effect mechanism of positive and negative sequence current control for DFIG under asymmetric fault

图4 中，↑表示物理量值上升；↓表示物理量值下降。由图4 可知，不对称故障下正序电流控制存在2 条耦合回路。一条是通过正序自阻抗和正序锁相环耦合的正序自阻抗回路；另一条是通过正序耦合阻抗、负序电流控制、负序锁相环耦合的正序耦合阻抗回路。在正序自阻抗回路中，正序定子电流经过正序自阻抗H++(s+jω1)使得正序端电压上升、正序转子电流下降，从而维持正序转子电流的稳定；在正序耦合阻抗回路中，正序定子电流经过耦合正序阻抗H-+(s-jω1)使得负序端电压上升、负序定子电流上升、正序端电压下降，进一步导致正序转子电流上升。故不对称故障下，正序电流控制经正序耦合阻抗、负序电流控制、负序锁相环耦合的回路是一个正反馈回路，不利于系统稳定。

为验证以上分析，构建传递函数GI（s）以分析不同控制参数对DFIG 正负序电流耦合的影响。定义传递函数GI（s）输入负序dq轴坐标系下负序转子电流，输出正序dq轴坐标系下正序定子电流。传递函数GI（s）框图如图5 所示。

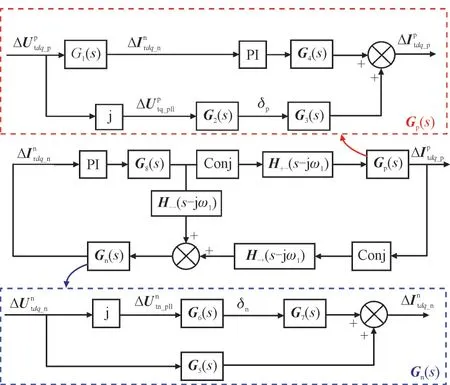
图5 传递函数GI（s）框图Fig.5 Block diagram of transfer function GI（s）

图5 中，Gp（s），Gn（s）分别为正序端电压到正序定子电流、负序端电压到负序定子电流的传递函数。

传递函数GI（s）的表达式为：

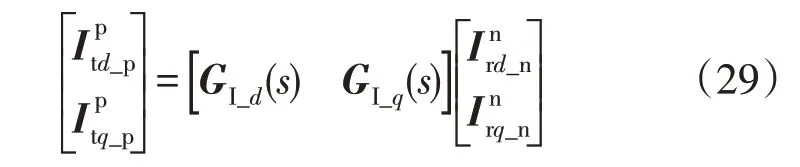
式中：GI_d(s)，GI_q(s)分别为负序d轴转子电流到正序d轴定子电流的传递函数和负序q轴转子电流到正序q轴定子电流的传递函数；分别为正序定子电流在正序d轴和q轴上的矢量分量；分别为负序转子电流在负序d轴和q轴上的矢量分量。

不同参数对GI_d(s)幅值的影响如图6 所示。

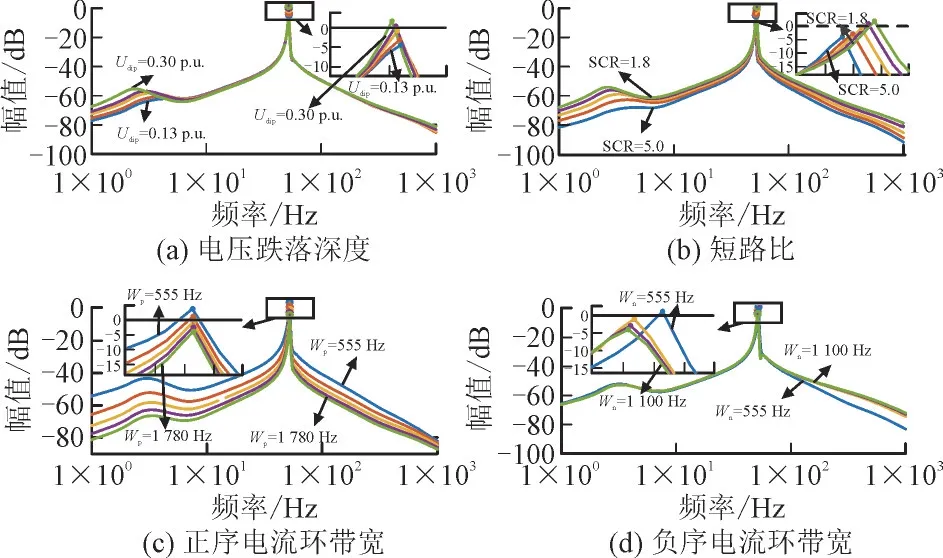
图6 不同参数对GI_d（s）幅值的影响Fig.6 Influence of different parameters on magnitude of GI_d（s）

由图6（a）可知，电压跌落深度越大GI_d(s)的幅值响应峰值越大，说明不对称故障越严重负序转子电流对正序定子电流的影响越大，DFIG 正负序电流耦合越深。由图6（b）可知，短路比越小GI_d(s)的幅值响应峰值越大，说明电网强度越弱负序转子电流对正序定子电流的影响越大，DFIG 正负序电流耦合越深。结合图3（a）和图3（b），可证明不对称故障下DFIG 正负序电流耦合作用实质是在电流控制中加入了一个正反馈回路，DFIG 正负序电流耦合作用越强对应正反馈回路效果越强，系统越不稳定。

由图6（c）可知，正序电流环带宽越大GI_d(s)的幅值响应峰值越小，说明正序电流环带宽越大负序转子电流对正序定子电流的影响越小，DFIG 正负序电流耦合越弱。由图6（d）可知，负序电流环带宽越大GI_d(s)的幅值响应峰值越小，说明负序电流环带宽越大负序转子电流对正序定子电流的影响越小，DFIG 正负序电流耦合越弱。结合图3（c）和图3（d），说明增大电流环带宽可有效减小DFIG 正负序电流耦合作用，从而使系统更加稳定。

3 仿真分析

为验证第2 章节分析，在Matlab 中建立DFIG接入弱交流电网的详细时域仿真模型，控制和主电路参数见表1。本文DFIG 参数参考GE 公司DFIG模型，设置功率为1.5 MW、端电压为690 V、风机频率为50 Hz。系统稳定运行后，在第1.5 s 时设置两相接地短路故障使系统进入故障持续阶段，在第3.0 s 时设置小干扰。不同风机控制参数对DFIG 正负序无功电流小扰动稳定影响如图7 所示。

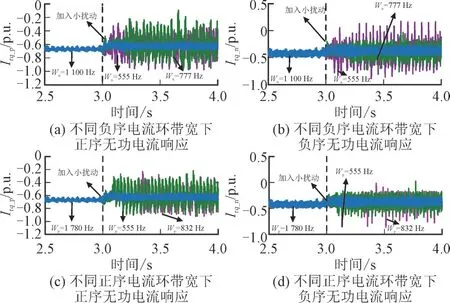
图7 不同风机控制参数对DFIG正负序无功电流小扰动稳定影响Fig.7 Influence of different DFIG control parameters on small disturbance stability of DFIG with positive and negative sequence reactive current

由图7（a）和图7（b）可知，在负序机侧电流环带宽为555 Hz 和777 Hz 的情况下，系统分别在3.0 s和3.2 s 处失稳，负序机侧电流环带宽上升至1 100 Hz 时系统保持稳定；由图7（c）和图7（d）可知，在正序机侧电流环带宽为555 Hz 和832 Hz 的情况下，系统分别在3.0 s 和3.3 s 处失稳，带宽为1 780 Hz时系统保持稳定。说明提高电流环带宽会减弱DFIG 的正负序电流控制耦合作用，从而加强DFIG在故障持续阶段的小干扰稳定性。

弱电网不对称故障下，不同电网参数对DFIG正负序无功电流小扰动稳定影响如图8 所示。

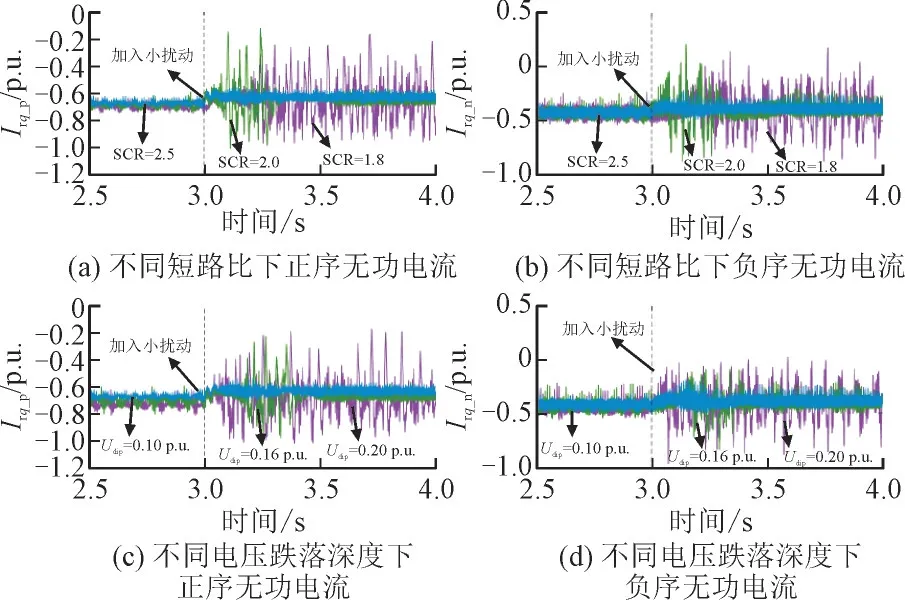
图8 不同电网参数对DFIG正负序无功电流小扰动稳定影响Fig.8 Influence of different grid parameters on small disturbance stability of DFIG with positive and negative sequence reactive current

由图8（a）和图8（c）可知，短路比为2.5 时系统稳定，短路比为2.0 时系统加入小扰动后发生震荡但最终稳定，而在短路比为1.8 经小扰动后系统失稳。图8（b）和图8（d）显示跌落深度为0.10 p.u.时系统稳定，0.16 p.u.时系统加入小扰动后发生振荡但最终稳定，0.20 p.u.时系统失稳。说明电网强度降低或电网跌落深度增加会加剧DFIG 的正负序电流控制耦合作用，从而降低故障持续阶段DFIG 小干扰稳定性。