面向新型电力系统的新能源与储能联合规划方法

2022-10-30刘沅昆张维静张艳侯孟希

智慧电力 2022年10期

刘沅昆，张维静，张艳，侯孟希

（1.清华大学电机工程与应用电子技术系，北京 100084；2.国网经济技术研究院有限公司，北京 102200）

0 引言

随着能源危机和环境污染的日益加剧，大力使用和发展非化石能源，尤其是以风能、太阳能为代表的新能源[1]，被能源行业视为减少温室气体排放、缓解气候变化和实现可持续性的最有效途径之一。凭借清洁、低碳等优势，新能源成为各国制定能源政策的主要选择[2]，在世界各国得到迅速发展。随着双碳时代的到来，构建以新能源为主体的新型电力系统是实现碳中和、碳达峰的主要举措。而电力系统的合理规划将是可持续发展战略的重要内容[3]。

传统电源规划的目标是在满足一定可靠性的基础上，寻求一个最经济适用的电源规划方案[4]，规划方法包括混合整体规划法和模拟进化方法等[5]。随着电力市场改革的不断深入，改变了原有以整个系统成本最小化或收益最大化为目标的集中电源规划方案[6]。电力市场背景下的电源规划与传统的电源规划区别[7-8]主要表现为：（1）电源规划的目标函数由垄断环境下整个发电系统总成本最低到市场环境下发电公司自身投资效益最高；（2）各发电公司的电源规划投资策略之间需要开展竞争；（3）发电公司在电力市场环境下面临的不确定因素更多、投资风险更大。

为了适应新的需求，基于电力市场环境下合理的电源规划有助于新能源消纳，实现投资利益最大化。文献[9]提出了一种新能源大规模并网的电源规划方法，考虑季节波动，针对典型时段进行系统调节能力评估。文献[10]提出了一种考虑碳约束的区域电源多阶段双层扩展规划方法，以最低成本进行多区域电力系统间的协调规划，实现了区域协同减排的目的，但未考虑电力市场的影响。文献[11]研究了电力市场中新能源发电规划，在下层市场问题的基础上，上层决定风电场的位置和容量决策，最大限度地提高以位置边际价格支付吸收风能的收入。文献[12]引入大量场景来获得负载和风能不确定性时的计算方案，开发了Benders 分解方法有效解决典型实例。文献[13]从分布式运营商角度进行电源规划，建立了主动管理模式下的双层优化规划模型，实现了利益双赢。文献[14]建立了一个随机双层混合整数优化模型，研究具有拓扑控制操作的电力市场环境下的风力发电规划问题，拓扑控制可以显著提高电力输送能力，实现更高的新能源穿透水平或更少的经济损失，然而，其均未考虑储能在1 d 之内的动态过程，且对新能源电站选址和规模确定的影响未深入研究。

大规模储能（Energy Storage System，ESS）技术的发展和应用，为增强电网灵活程度，提高风电消纳能力提供了全新的解决思路。应仔细选择新能源电站的选址和规模[15]。因此，应采用考虑所有关键因素的分析方法，如负荷、风力资源、现有发电资产和电网配置，以支持这些决策，电网应遵循市场规则来规划负荷和供应[16]。

由此，本文研究考虑电力市场调度的新能源与储能联合规划方法，提出基于典型日的双层规划方法（Bi-Level Programming，BLP）。上层规划用来模拟投资主体，下层规划用来模拟市场调度。利用IEEE14 节点算例对模型的有效性进行验证，对储能在含风电系统中的作用进行分析。

1 电力市场环境下的规划场景

1.1 电力市场运营模式

电力市场调度的目的是实现资源的合理配置，在电力市场环境下运营模式主要包括[17-19]：（1）垄断运营模式，能够实现电网设施的统一规划，但在电力供求关系缓和的情况下存在明显的缺点，效率、效益无法提高；（2）发电竞争模式，即局部垄断和局部竞争的模式，在发电部分加入独立的发电企业，增加了竞争压力，推动了零售市场的出现；（3）电力运转模式，即发电、输电和配电相互分离独立的模式，实行竞价上网；（4）配电开放模式，即配电环节从垄断模式中分离出来，发电、输电和配电三者之间存在买卖关系，使电力成为一种商品，实现了电力市场经济。

本文假设投资主体追求利益最大化，电力市场调度追求社会福利最大化，即碳排放和弃负荷最少。

1.2 典型日选取

本文通过选取典型日的方式进行规划。典型日的选取[20]既要考虑日常运行特点也要考虑规划方案应对极端情况的能力，因此本文采用“代表日+极端日”的思路，即选取表征四季正常变化的季节代表日和体现系统极端运行条件的多个极端日。极端日可选取为温度最高、温度最低负荷所在日、系统最大负荷所在日、新能源小时穿透率最大或最小所在日、重大节假日所在日等[21]。典型日的选取旨在电源投资决策模型中详细考虑时序运行约束，在确定电源最优容量组合的同时考虑新能源波动性对系统灵活性影响[22]。

2 双层规划模型

双层规划模型是一种具有2 层递阶结构的系统优化模型[23]，本文所提双层规划模型中，上层模型从投资主体角度出发，目的是通过对新能源和储能装置进行合理选址定容，达到净利润最大。下层模型是考虑电力市场调度规则的出清模型，调度目标是保证电网安全的前提下实现社会福利最大化，本文设置为碳排放和弃负荷最小。上下层模型之间相互影响[24-26]，上层模型将新能源和储能的配置方案传递给下层模型，下层模型基于上层决策的配置方案和市场调度规则求解出各典型日调度成本的期望值，并将结果反馈给上层。上层基于反馈结果对配置方案进行修正，再次优化新能源和储能的配置方案，如此循环往复，直至迭代收敛，即新能源和储能的配置方案不再变化，得到最优的选址定容结果。利用该双层模型得到的最优配置方案综合考虑了投资主体的利益与实际调度运行情况。具体模型如图1 所示。

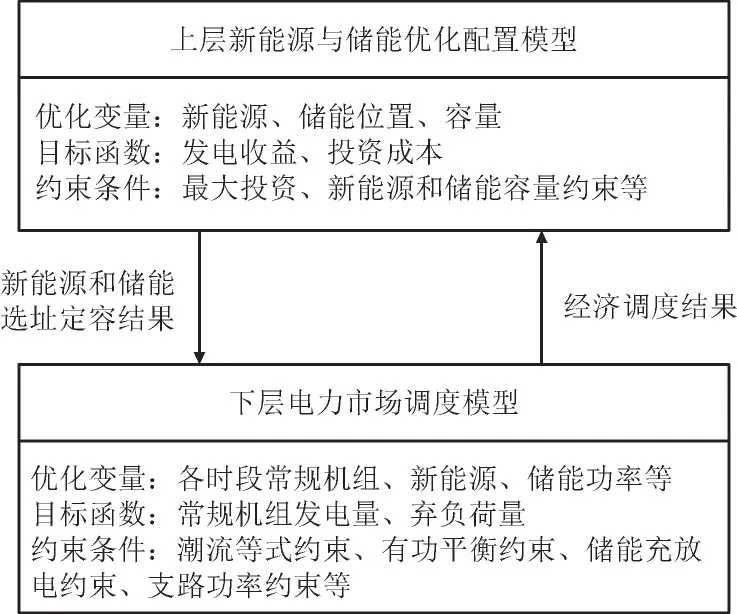
图1 双层规划模型Fig.1 Bi-level programming model

2.1 上层优化配置模型

上层模型从投资主体角度出发，通过对新能源和储能装置进行合理选址定容，达到净利润最大的目的。综合考虑发电收益和投资成本2 个目标建立规划模型，目标函数为：

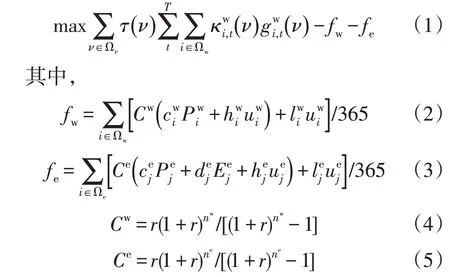
式中：为售电电价；ν为第ν个场景；Ων为所有场景ν构成的集合；τ(ν)为场景ν的概率；T为场景ν的分时段数；Ωw为新建新能源机组集合；为场景ν下t时刻新能源机组i的有功出力；Ωe为新建储能装置集合；r为贴现率；fw为新能源机组固定投资和年运行成本折算到每日的成本；nw为新能源机组寿命；为单位容量新能源机组i的单位容量投资费用；为新能源机组i的规划容量；为0-1 变量，为新能源机组i是否安装；为新能源机组i的固定投资费用；为新能源机组i的年运维费用；fe为储能装置固定投资和年运行成本折算到每日的成本；ne为储能装置寿命；为单位功率储能装置j的投资费用；为单位容量储能装置j的投资费用；为储能装置j的规划容量；为储能装置j的规划功率；为0-1 变量，为储能装置j是否安装；为储能装置j的固定投资费用；为储能装置j的年运维费用。

对应的约束条件如下：

1）最大投资约束。

式中：C为总投资的最大费用。

2）最大允许功率和允许容量约束。

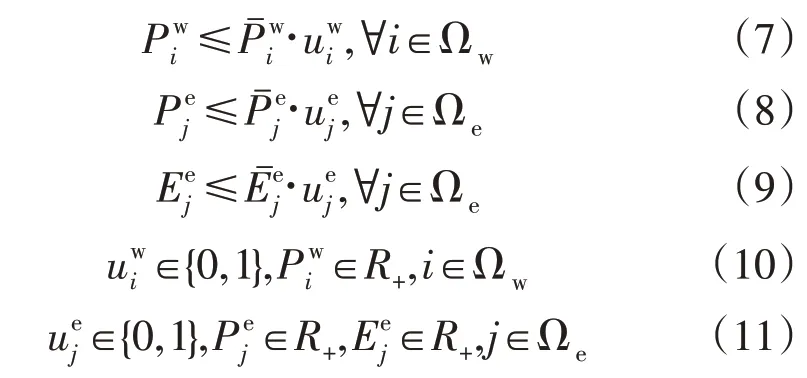
2.2 下层电力市场调度模型

下层模型是考虑电力市场调度规则的出清模型，调度目标是保证电网安全的前提下实现社会福利最大化，综合考虑常规机组发电量和弃负荷最小建立规划模型[27-28]，目标函数为：

式中：gm(ν)和gw(ν)分别为场景ν下常规机组出力变量和新能源机组出力变量组成的向量；pe(ν)和Ε(ν)分别为场景ν下储能装置运行功率变量（包括充电和放电）和剩余电量变量组成的向量；βe(ν)为0-1 变量组成的向量，为场景ν下储能装置的充放电操作；ps(ν)为场景ν下各节点弃负荷电量组成的向量。

对应的约束条件如下：

1）新能源机组i的出力范围约束。

式中：ki,t为t时刻节点i处新能源出力系数；为t时刻常规机组i的有功出力。

2）常规机组i的出力范围约束。

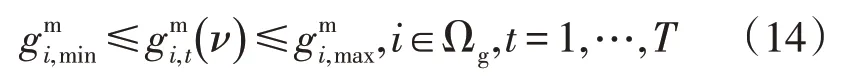
3）常规机组i的爬坡约束。

式中：Ru,i和Rd,i分别为常规机组i的最大爬坡和滑坡速率。

4）储能装置j的放电功率约束和充电功率约束。

5）储能装置剩余电量范围约束。

式中：Ej,t为t时刻储能装置j的剩余电量。

6）储能装置j的充放电约束。

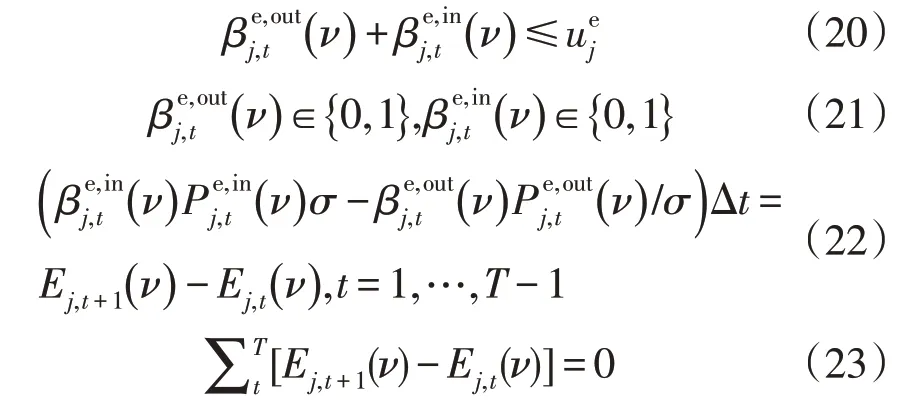
其中，式（23）为储能装置j在T个时间段内的充电量等于放电量。

7）支路潮流约束。

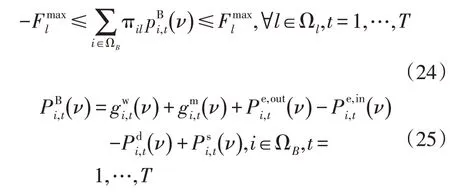
式中：πil为电网的潮流分配矩阵；为支路l的最大允许传输功率；为t时刻节点i的注入功率；为t时刻节点i的负荷；为t时刻节点i的弃负荷电量。

8）弃负荷量约束。

9）电力平衡约束。

3 双层规划模型求解

3.1 模型转化

约束式（22）中含有整数变量与连续变量的乘积项，难以直接求解，因此引入充电约束松驰变量和放电约束松驰变量，使用大M法写成等价的混合整数规划形式，具体如式（28）—式（31）所示。

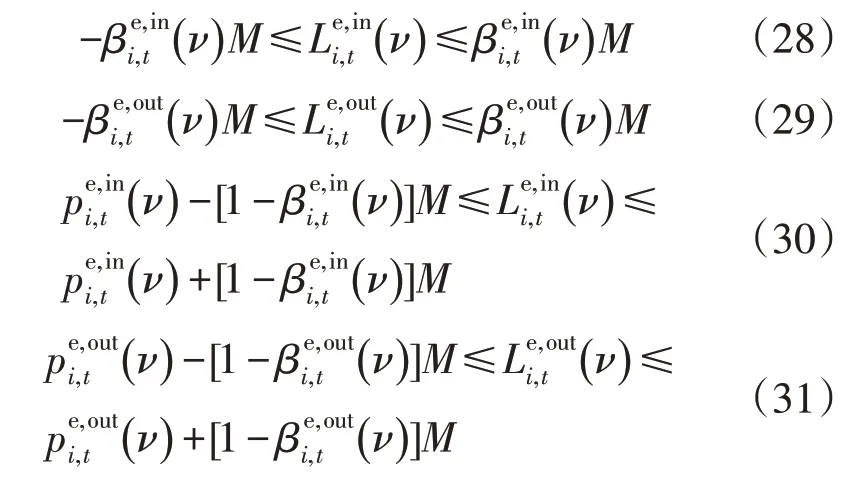
由于原规划问题为双层混合整数规划问题，难以直接求解，因此本文将其分解为1 个主问题和2 个子问题的形式，然后通过迭代的方式进行求解。

为叙述方便，首先将原问题写成如下紧凑形式：

目标函数为：

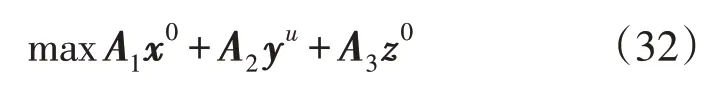
约束条件为：

其中，x0={Pw,Pe,Ee}，z0={uw,ue}，βu={βe}，yu={gw,gm,pe,E,Le,pB,ps}，A1，A2，A3，A4，A5，B1，B2，B3，B4，B5，B6分别为相应维度的系数矩阵；0 代表规划阶段的物理变量；n代表调度优化阶段的物理变量。

不难看出，当固定βu(ν)为βu,q(ν)时，式右侧为线性规划问题，写成其KKT（Karush-Kuhn-Tucker）条件形式为：

式中：πq为对偶变量；◦为2 个向量对应元素相乘。因此，式（38）可转化为一系列混合整数规划约束，可通过本文所述算法进行求解。

3.2 分解重构迭代算法

首先，将下层问题分解为2 个子问题：

子问题1（SP1）：

子问题2（SP2）：

然后，可通过如下求解步骤进行迭代求解：

步骤（1）：设置优化算法中的上限LB=-∞，优化算法中的下限，ν∈Ων，迭代次数j=1；

步骤（2）：求解主问题（MP）

式中：Θ 为新能源与储能选址定容结果。

4 算例分析

4.1 数据说明

本文所提算法可针对多个典型场景进行规划求解，且典型场景越多，分时段数越多，规划结果越客观。为简便起见，本文以IEEE-14 节点系统为例，且仅考虑光伏和化学储能装置的规划，系统示意图如图2 所示。将所有发电机最大出力设置为150 MW，最小出力设置为65 MW。所有节点负荷放大2.5 倍，所有支路最大输电容量设置为150 MVA。时间段数T设置为24，典型日场景数设置为1，并假设新能源和储能装置只安装在同一节点。各时刻的新能源出力和负荷水平的具体信息如表1 所示。

图2 IEEE-14节点系统示意图Fig.2 Schematic diagram of IEEE 14-node system

系统相关参数设置如下，r=8%，nw=20，ne=20，C=10（亿元），为方便起见，本文仅考虑分时电价场景，假设08:00-20:00 新能源售电价为0.595 3 元/kWh，其余时刻新能源售电价为0.515 3 元/kWh。

4.2 IEEE-14节点系统算例分析

新能源与储能安装在同一个节点，不另外规划储能节点，可以节约占地成本。规划后的新能源分别在节点2 和3 处接入装机容量为150 MW 和16.74 MW 的光伏机组。

不同节点的光伏有功出力随时间的变化如图3所示。

图3 不同节点的光伏出力Fig.3 Photovoltaic output of different nodes

其中光伏1 接在节点2 处，光伏2 接在节点3处。模型求解结果并未得出储能装置结果，主要是因为电价较低时，储能装置成本较高，弃光成本远小于投资储能的成本。该结果与实际规划情况吻合，验证了模型建立与求解算法的有效性。

4.3 电价对规划结果的影响

假设新能源售电价格变为原来的2 倍，分析电价变化对规划结果的影响。电价提升2 倍后分别在节点2 和3 处接入装机容量为37.75 MW 和150 MW的光伏组件。

电价变为2 倍后不同节点的光伏有功出力随时间的变化如图4 所示。其中光伏1 接在节点2处，光伏2 接在节点3 处。模型求解结果并未得出储能装置结果，主要原因还是电价不高，弃光损耗小于安装储能装置成本。

图4 电价变为2倍后的光伏出力Fig.4 Photovoltaic output of different nodes after electricity price is increased by 200%

假设将所有时刻电价提高3 倍，即高电价规划结果对比。电价提高3 倍后新能源与储能安装容量分别在节点8 和12 处接入装机容量为87.63 MW 和106.26 MW 的光伏组件，在节点12 处接入储能装置，储能规划功率为5.19 MW，储能规划容量为5.46 MWh。

电价提高3 倍后不同节点的光伏有功出力随时间的变化如图5 所示。

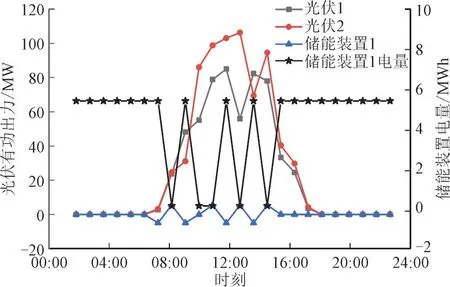
图5 电价提高3倍后光伏及储能出力Fig.5 Photovoltaic output and energy storage output after electricity price is increased by 300%

其中光伏1 接在节点8 处，光伏2 接在节点12处，储能装置1 接在节点12 处。可见，当假设电价抬高到一定程度时，模型求解得出储能装置选址定容结果，主要是因为高额电价足以支付储能装置安装成本，符合实际情况，验证了模型建立和求解算法的有效性。

假设将所有时刻电价提高5 倍，即高电价规划结果对比。电价提高5 倍后新能源与储能安装容量为，在节点1 和9 处接入装机容量为37.75 MW 和150 MW 的光伏组件，在节点1 和9处接入储能装置，储能规划功率分别为4.08 MW和14.02 MW，储能规划容量分别为15.31 MWh 和37.42 MWh。

电价提高5 倍后不同节点的光伏有功出力随时间的变化如图6 所示。其中光伏1 和储能装置1接在节点1 处，光伏2 和储能装置2 接在节点9处。可见，当假设电价继续抬高到一定程度时，与3倍电价相比，模型求解得出更多节点储能装置选址定容结果。

图6 电价提高5倍后新能源安装点处安装容量及储能剩余容量Fig.6 Installation capacity and remaining energy storage capacity at renewable energy installation point after electricity price is increased by 500%

在高电价时，储能装置在光伏出力较大且电网无法消纳过多的光伏电量时开始充电，以便减少弃光，充放电状态切换频繁，主要是因为光伏出力因气候原因有较强的波动，配合光伏出力的波动切换充放电状态，提高了对光伏发电的消纳能力。

通过对比可知，当电价较低时，仅靠平移白天光伏发电量至夜间，储能装置由于成本太高，较难盈利，只有当电价高达一定程度，或储能成本降低至一定程度，才可能盈利。因此，为追求储能的盈利，还需进一步开放储能的辅助服务市场，从多元角度来获利。