区域光伏发电出力特性分析研究

吕清泉，张珍珍，马彦宏，张健美，高鹏飞，蒋婷婷，朱红路

（1.国网甘肃省电力公司电力科学研究院，甘肃省 兰州市 730070；2.国网甘肃省电力公司，甘肃省 兰州市 730000；3.华北电力大学新能源学院，北京市 昌平区 102206）

0 引言

我国光伏发电发展迅猛，“十二五”期间光伏发电装机规模增长168倍，并于2015年成为世界光伏装机第一大国。2016—2020年保持高增速，2020年底累计装机达到240 GW，光伏发电已经超过风电，在中国成为第三大电源。在“30·60”目标指引下，光伏发电在我国能源供给结构中将会占据更为重要的地位[1]。但是由于光伏出力具有明显的周期性和随机波动性特征，当光伏电站大规模接入电网时，对电网的调峰能力和调频能力是一个极大的考验[2-6]。光伏发电的渗透率上升，超出火电机组的调节能力，“弃光”现象就会发生。以中国甘肃省为例，截至2019年底，全省新能源累计受限电量为23.9亿kW·h，其中：风电受限电量为18.8亿kW·h，弃风率为7.62%；光伏受限电量为5.1亿kW·h，弃光率为4.11%。研究区域光伏的出力特性，有利于了解规模化光伏并网对电力系统的影响，从发电端分析“弃光”现象的产生原因，提高输出功率的可控性[7]，进而实现规模化光伏发电的高效接入。

为提高光伏发电消纳水平，国内外对光伏出力特性的研究日益增多。文献[8]采用指标“季节属性”来表征光伏出力的持续时间长度，以光伏全日最大出力和季节属性为标准，将光伏典型出力曲线按标准分为9类。文献[9]用相关性、互补性和随机性指标对新能源基地出力进行评价，并建立了新能源基地的三维出力模型。文献[10]考虑了新能源发电不同时间尺度的时序出力特性、出力变化特性等，建立了新能源发电出力自然特性指标体系。文献[11]对新能源场站总出力与负荷进行Copula建模，计算出区间尾部相关系数和Spearman秩相关系数，评估新能源互补后总出力与负荷的正相关性。文献[12]利用概率潮流法(probabilistic power flow，PPF)评估光伏发电的不确定性对传输系统性能的影响。文献[13]提出了不同时间尺度下新能源出力特性的评估体系，并对青海省某风电站的出力过程进行了特性分析。

上述研究为区域光伏出力特性的研究提供了思路，但是现有区域光伏出力特性的研究缺乏光伏场站-区域层级样本数据，多停留在光伏场站出力概率模型建模及出力特性分析。为更好地揭示区域光伏发电出力特性，本文以甘肃省10个区域的17个光伏电站为例，分析了甘肃省光伏发电的出力特性以及在时间、空间上的分布特点，研究了光伏出力的波动特性，并将不同区域间光伏出力进行互补特性研究，为区域光伏消纳问题的分析提供参考，为规模化光伏发电发展规划的制定提供借鉴。

1 区域太阳能资源特性和整体出力情况

1.1 甘肃省太阳能资源情况和光伏装机

甘肃省具有丰富的太阳能资源，年太阳能总辐射量为4 800～6 400 MJ/m2，年资源理论储量为670万亿kW·h。其中，酒泉、嘉峪关、武威、张掖、金昌等区为光伏一类资源区，其他地方为二类资源区。本文所用的光伏电站数据是甘肃省10个区域17个独立电站(对应编号为1—17)2019年全年输出功率数据，数据时间分辨率为1 h。

1.2 整体出力情况分析

图1为电站分别在2019年3月15日、6月15日、9月15日和12月15日这4天的出力曲线。由图1可知，光伏出力具有明显的周期性，呈先上升后下降的趋势；同时存在随机性，体现为每个周期内的波动最大出力值是不确定的。

图1 17个光伏电站不同时刻出力曲线Fig.1 Output curves of 17 photovoltaic power stations at different time

由于光伏出力具有一定的波动特性和不确定性，在不同的时间尺度下，单一的出力值不具有代表性。求取新能源出力数据的最大值和平均值，有助于从全局角度评估光伏电站的出力水平和区域的光伏出力情形。P1,P2,P3,…,P n是统计周期内光伏电站的一组出力，则最大值Pmax和期望Paverage分别表示为：

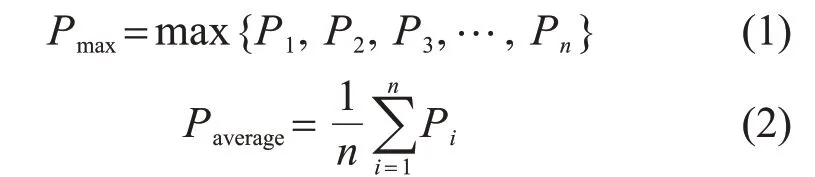
对离散的出力值进行归一化，将0～1划分为若干个等间距区间，统计出力值落在每一区间的次数，落在0.5～1区间内的概率称为半载以上概率。求取光伏的半载出力概率p，在一定程度上反映了各风电场或者光伏基地的出力水平。设定N0.5～1是比值在0.5～1区间内的次数，N是统计的总频次，则

甘肃省各区域光伏电站出力的最大值、期望值和半载以上概率如表1所示。酒泉位于甘肃省西北角，占地面积较大，光伏电站数量最多且分布分散，各电站出力最大值差异较大，变化范围为0.63～0.85 pu；半载以上概率水平差异较大，变化范围为0.12～0.30；出力期望除电站4都在0.2 pu以上。张掖处于甘肃省中部狭长地带，占地面积较小，光伏电站数量较多，这些电站出力情况较为相似，出力期望均大于0.2 pu，半载以上概率均超过0.18。金昌紧邻张掖，2个电站出力情形相似，出力期望均为0.2 pu，半载以上概率均为0.19。武威位于甘肃省中部，该区域中电站13的最大出力、出力期望和半载以上概率在所有电站中最大。白银电站最大出力为0.90 pu，出力期望为0.30 pu，出力情形较为良好。兰州和定西的光伏电站半载以上概率都不大于0.15。

表1 光伏电站出力分析Tab.1 Output analysis of photovoltaic power stations

最大出力表征光伏电站一天之内各时段达到的最大出力，半载出力以上概率体现了光伏电站的有效发电时长。总体来看，光伏电站最大出力的地域性不明显，酒泉、张掖、金昌、武威和白银等地半载以上概率更高，即这些区域光伏电站的停机和低发情形更少。

2 典型季节下的出力特性

2.1 日均出力曲线

以容量为50 MW的电站14为例，对当月每天同一时刻出力取平均值，得到每月日均出力曲线如图2所示。光伏日间出力在14:00附近达到最大，能达到电站总容量的60%。整体来看，光伏电站在7—9月的平均出力水平较高，在1、4、5、6、10、11月的平均出力水平较低。按照季节划分，冬季出力水平较低，夏季出力水平较高。

图2 光伏月度日均出力曲线Fig.2 PV monthly average daily output curves

2.2 典型日出力曲线

图3为电站14的典型日出力曲线。由于每天日间辐照量、温度和湿度具有不确定性，单个最大出力值不具有代表性，但各个季节出力时间是基本确定的。由图3可知，光伏电站在夏季日出力时间最长，从06:00到22:00，共计16 h；在冬季日出力时间最短，从09:00到19:00，共计10 h；春、秋季出力时间介于两者之间。夏季日间出力波动较大，秋季出力变化平缓。

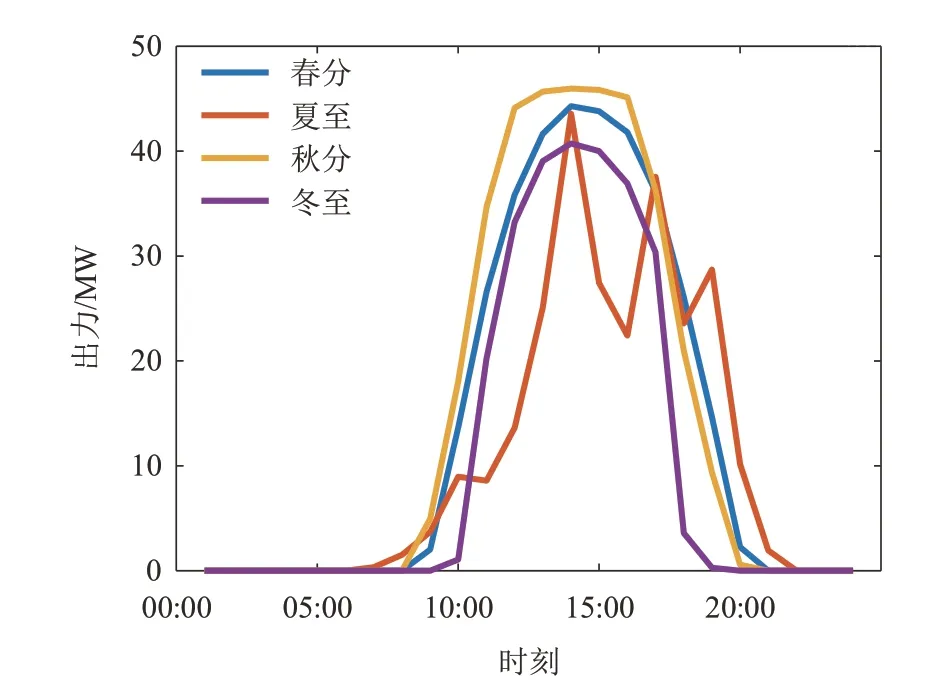
图3 典型日出力曲线Fig.3 Typical daily output curves

2.3 典型天气日出力曲线

图4为电站14在不同天气条件下的出力曲线，时间分别是12月14日、12月15日、12月16日和12月17日。由于相隔天数很近，电站的日间出力时间相同，从09:00—19:00，在14:00附近达到峰值；晴天的出力峰值最大，达到装机容量的80%以上，累积出力最大，出力变化率最平缓；多云天气的出力峰值较大，但出力下降速度较快，波动较大，累积出力较低；阴天与晴天相比区别不大，但出力峰值略有降低；小雪天气的出力水平很低，出力峰值只能达到装机容量的60%。

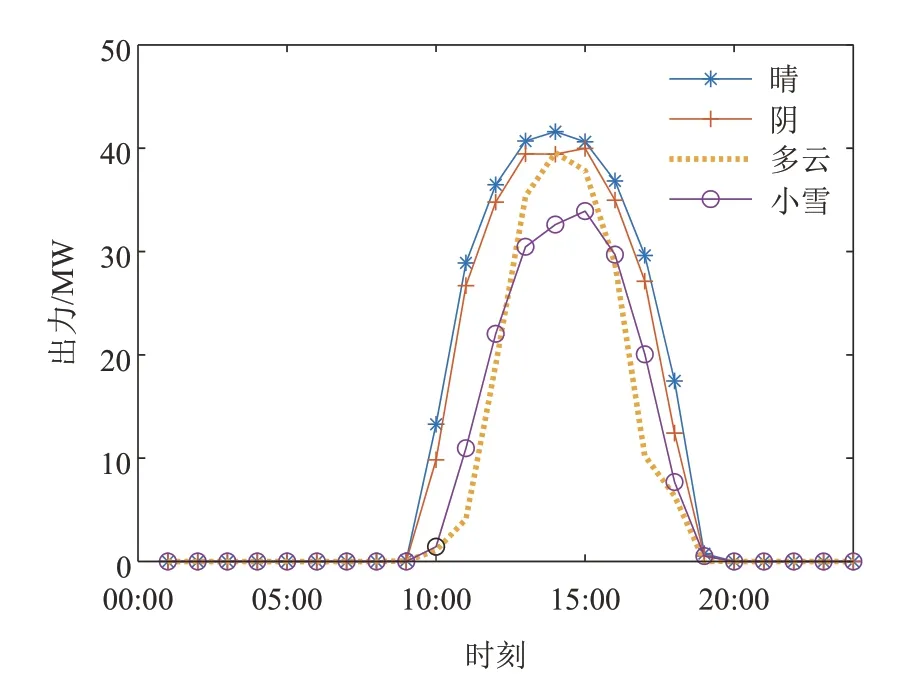
图4 典型天气日出力曲线Fig.4 Daily output curves of typical weather

3 波动特性分析

3.1 光伏出力波动的统计特性

光伏出力与辐照量呈正相关，日间出力是一条先上升后降低的曲线，在整体趋势上体现为周期性。由于辐照量的变化存在的一定的随机性，光伏出力的波动也存在一定的随机性。光伏电站在夜间出力恒定为零，波动也为零，因此剔除夜间出力，只对白天时段的波动进行分布统计。

在统计周期T内，出力的变化视为一次波动ΔP，表示为

图5为电站14截取某一段出力的波动序列。波动的分布特性用概率密度函数来体现。在统计学中，常见的概率分布函数有正态分布、Logistic分布和T-location分布。

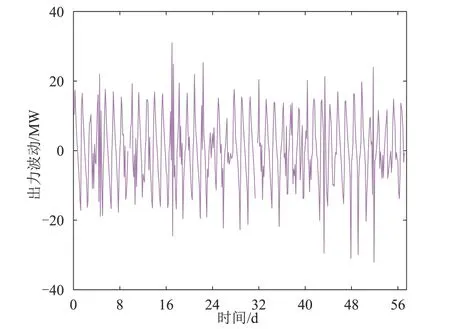
图5 波动时序曲线Fig.5 Fluctuation series curve

以电站14为例，在2019年1月1日至2019年12月30日分辨率为1 h的出力数据中，随机取1 000个连续出力值，相邻出力值之差视为一次波动，得到电站的一段波动序列。

基于最大似然估计方法，分别用正态分布函数、Logistic分布函数、T-location分布函数对波动的分布进行拟合[14]，如图6中曲线所示，实际概率分布如图6中直方图所示。

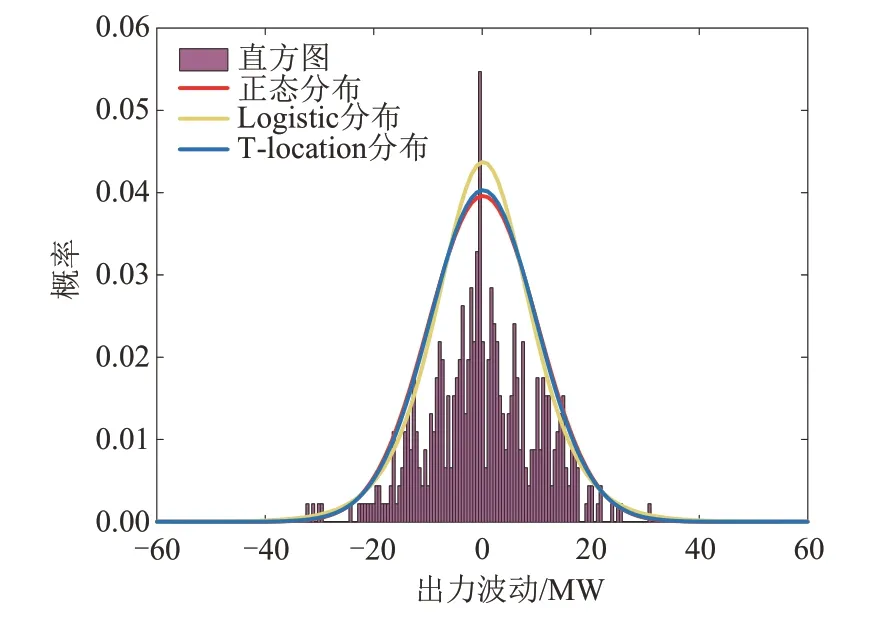
图6 电站12三种分布函数的拟合效果对比Fig.6 Comparison of fitting effects of three distribution functions of power station 12

3.2 拟合效果评估指标

用评价函数可以对分布函数的拟合效果进行评估。和方差(sum of squares error，SSE)是拟合值相对于原值的误差平方和，该值越趋向于0，代表拟合效果越好。设yi是第i个出力值，ŷ是y的拟合值，则和方差为

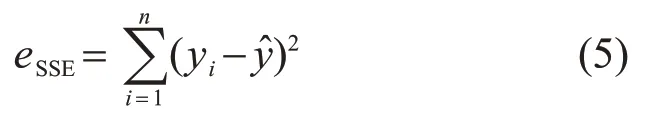
为了分析不同光伏电站日间出力波动的分布特性，选取17个光伏电站全年分辨率为1 h的实际出力数据来进行分析，得到光伏电站日间波动在不同拟合分布下的和方差，结果如表2所示。通过分析可知，对于不同地理位置、不同装机容量的光伏电站，出力序列的波动在正态分布或T-location分布下都有很好的拟合效果。

表2 不同拟合方式的方差Tab.2 Variance of different fitting methods

4 光伏出力的集群特性

4.1 光伏出力相关性

相关系数∂是一个统计学指标，用于描述2个变量之间的变化趋势及相关程度[15]。光伏出力是离散的随机变量，假设在t时刻2个光伏电站出力分别为Psolar1和Psolar2，在统计周期内其期望值分别为Ep-solar1和Ep-solar2，则

以电站9、12为例，计算2个电站每月的日间出力相关性系数，结果如图7所示。可见，相关系数都处于0.5～1.0，说明2个出力变量具有很强的相关性。相关性在全年的变化比较显著，6—11月相关性较小，1—5月和12月相关性较大。

图7 光伏电站出力相关系数Fig.7 Output correlation coefficients of photovoltaic power station

4.2 区域光伏出力相关性

以每一区域多个光伏电站的出力之和作为区域总出力，计算不同区域光伏出力的相关性，结果如表3所示。由表3可知，区域出力相关性多在0.8～0.9的范围内，线性关系较强。由于辐照度在一天中的变化比较相似，因此不同区域之间出力情况也比较类似。

表3 不同区域间光伏总出力相关系数Tab.3 Correlation coefficients of total photovoltaic output among different regions

4.3 光伏同时率分析

同时率s又称为集群效应系数，是指统计时段内最大可能出力与相应的总装机容量之比[16]，可表示为

式中：P∑为光伏电站集群统计时段内的最大出力之和；Ci为第i个光伏电站的额定容量。

出力同时率反映了光伏电站集群的最大可能出力，体现了光伏电站集群的综合利用效率。现以甘肃省4个区域(张掖、武威、金昌和酒泉)的光伏电站总出力数据为例，计算同时率的概率分布如图8所示，可以看出，各区域光伏出力同时率主要分布在[0.7,0.9]区间。张掖、金昌地区同时率相对于其他地区较大，武威地区相对较小。将4个区域的总出力作为集群计算其同时率分布，结果表明：光伏电站集群较不同区域间的同时率分布差异降低，在提升光伏利用率的同时减小了线路的负载压力。

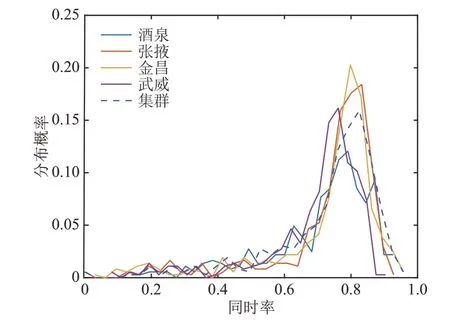
图8 区域光伏总出力同时率概率分布曲线Fig.8 Probability distribution curves of simultaneous rate of regional photovoltaic total output

同时率越高，限制光伏电站发电的情况将会越多，当限制发电频繁发生时，不仅是对能源的浪费，对于调度运行也是一种挑战。调度根据光伏集群出力的同时率、网络阻塞和地区负荷差异来确定弃光容量[17]，对于提高光伏发电接入水平具有积极意义。

5 结论

以甘肃省17个光伏电站的全年实测出力数据为分析对象，从区域光伏发电的日出力特性、季节特性、波动性和同时率等方面对其出力特性展开研究，得到以下结论：

1）甘肃省光伏出力具有区域差异，酒泉、张掖、金昌和武威等光伏资源一类地区出力大于0.5 pu的天数更多；酒泉、武威地区电站出力情形差异较大；张掖、金昌地区电站出力情形比较相似；白银虽属于光伏资源二类地区，但电站最大出力和出力期望都属于较高水平；兰州和定西地区整体出力水平较低。

2）光伏电站的出力波动具有一定的随机性，概率分布更接近于正态分布或T-location分布。

3）不同区域之间的光伏电站出力具有很强的相关性，在对光伏功率进行预测时，需要考虑到不同电站的线性关系，以提高预测的准确程度；在进行电力调度时，需要考虑区域负荷差异和网络阻塞情形，合理制定调度计划，以免产生“弃光”现象。

4）受气象因素影响，光伏日间出力波动可能较大。将张掖、武威、金昌和酒泉地区的光伏出力作为集群，其同时率较组合前差异降低，光伏出力波动情况得以改善，对于光伏发电安全经济并网有一定参考意义。