基于曲率滤波和N-P准则的路面裂缝识别方法*

王墨川,何 莉,胡成雪,陶 健,张德津

(1.湖北工业大学电气与电子工程学院，湖北 武汉 430068；2.深圳大学机电与控制工程学院，广东 深圳 518060；3.深圳大学广东省城市空间信息工程重点实验室，广东 深圳 518060)

1 引言

裂缝是沥青路面的主要破损情况，准确高效地检测裂缝对路面养护有着积极的意义。沥青路面图像纹理复杂，裂缝形状多样、尺度多变，特别是细小裂缝与路面背景对比度低，使沥青路面裂缝自动检测有一定困难。

Cheng等[1]基于背景差法消除光照不均匀，对于阴影等低频噪声的处理效果较好，但容易平滑掉裂缝信息。基于多尺度几何的Ridgelet方法[2]实现了裂缝目标的有效增强，但模型参数选择复杂，算法适应性一般。基于阈值化的图像分割得到了广泛研究，Jitprasithsiri等[3]使用不同路面裂缝图像对比了不同阈值分割方法，发现回归方法的效果最好。Oh等[4]针对回归方法的缺点，提出了一种迭代的裁剪法，使用均值和方差去除噪声像素，保留裂缝像素。许多研究人员将机器学习的方法用于路面裂缝识别[5,6]，将路面图像划分成许多小的子图像，然后针对子图像进行特征提取构建特征向量，进而通过样本训练实现对新样本分类。Oliveira等[5]计算一系列统计量，如均值、方差，作为类别特征值。Nguyen等[6]将各向异性作为类别特征。对于路面裂缝的连接，邹勤等[7,8]采用了分别基于最小生成树和最短路径的路面裂缝连接算法，此类算法根据距离因素，设置经验阈值对目标点内、外连接，对相互邻近、交叉的复杂裂缝(如龟裂)的检测效果不理想。

本文提出一种基于曲率滤波和N-P准则的路面裂缝识别方法。通过改进曲率滤波算法平滑干扰并保留裂缝信息，采用二次分割及噪声去除的方法对裂缝进行定位，基于N-P准则实现裂缝片段端点的连接，最终实现裂缝检测。

2 图像特征分析

裂缝图像具有如下特征：(1)灰度特征：裂缝相对于纹理是一些灰度值较低的像素集合，裂缝主要分布在灰度直方图左侧的一小部分区域内，如图1a所示。(2)几何特征：裂缝的几何形状接近线状和带状，有较大的长度和较大的长宽比，而纹理的长度较短，或呈点状，如图1b所示。(3)位置特征：复杂裂缝由多条简单裂缝发展而来，即空间上距离较近的简单裂缝，可能相互渗透和影响，发展为复杂裂缝，如图1c所示。(4)方向特征：路面裂缝的局部方向与裂缝的整体方向基本一致，如图1c所示。

一幅含有裂缝的图像由3部分组成，设S(I)表示含有裂缝的路面图像，则可表示为：

S(I)=Sb(I)+Sn(I)+Sc(I)

(1)

其中，Sb(I)是纹理噪声信号，Sn(I)是随机噪声信号，Sc(I)是裂缝信号，I是像素坐标{x,y}。由于Sb(I)和Sn(I)的存在，使得Sc(I)淹没其中，很难直接提取出Sc(I)。考虑干扰滤除和裂缝保持要求，本文通过结合最小矩形切平面和最小三角形切平面、修正正则化能量的曲率滤波，实现消除随机噪声、平滑纹理，并尽可能保留裂缝的目的。在此基础上，本文参考裂缝灰度特征，以子块为单元，基于直方图拟合的方法粗分割Sc(I)与Sb(I)，去除不满足要求的区域，获得感兴趣区域ROI(Region of Interest)，通过ROI子块对非ROI子块进行分类后，对所有子块再次分割；根据几何特性，去除与裂缝具有相似灰度特征的Sb(I)；最后融合位置和方向信息，连接断裂的裂缝片段，实现裂缝完整检测。本文方法过程如图2所示。

3 路面裂缝定位

3.1 基于曲率滤波的图像平滑

全变分曲率滤波TVF(Total Variation Filter)和高斯曲率滤波GCF(Gaussian Curvature Filter)[9]是常用的滤波方法。对比发现,前者能更有效地去除噪声，后者能更好地保持图像的边缘和纹理细节。本文组合全变分曲率滤波、高斯曲率滤波的最小矩形切平面、最小三角切平面，通过邻域均值修正正则能量项，在去除干扰的同时保留裂缝边缘信息。曲率滤波[9]的思想是定义一能量泛函，这个能量泛函的值越小，变量就越接近于期望的结果。能量函数的能量公式如式(2)所示:

E(S)=E0(S,I)+E1(S)

(2)

其中，E(S)表示总能量，E0(S,I)表示拟合项能量，E1(S)表示正则化能量。能量泛函的演化过程如图3所示，因为拟合项能量E0(S,I)在增加，正则化能量E1(S)在减少，且目标是使总能量E(S)减少，所以从曲率滤波的角度得出在优化过程中正则化能量是主导部分，先将曲率正则化能量降至极小值，再观察总能量决定是收敛还是继续迭代。

本文改进曲率滤波算法的具体步骤如下:对输入图像U(i,j)构造最小矩形切平面和最小三角形切平面，如图4所示。

d1=(U(i-1,j-1)+U(i-1,j)+U(i-1,j+1)+U(i,j+1)+U(i,j-1))/5-U(i,j),

d2=(U(i-1,j+1)+U(i,j+1)+U(i+1,j+1)+U(i-1,j)+U(i+1,j))/5-U(i,j),

d3=(U(i+1,j-1)+U(i+1,j)+U(i+1,j+1)+U(i,j-1)+U(i,j+1))/5-U(i,j),

d4=(U(i-1,j-1)+U(i,j-1)+U(i+1,j-1)+U(i-1,j)+U(i+1,j))/5-U(i,j),

d5=(U(i-1,j)+U(i,j-1)+U(i-1,j-1))/3-U(i,j),

d6=(U(i-1,j)+U(i,j+1)+U(i-1,j+1))/3-U(i,j),

d7=(U(i,j-1)+U(i+1,j)+U(i+1,j-1))/3-U(i,j),

d8=(U(i,j+1)+U(i+1,j)+U(i+1,j+1))/3-U(i,j),

dm=min{|di|,i=1,…,8},

通过多次实验发现，曲率滤波的正则能量项仅考虑了曲率能量的约束，对于路面裂缝图像，图像的裂缝信息被严重污染，几何结构被严重破坏，若使用结合的投影算子对能量函数进行迭代，如图5a所示，总能量和数据拟合项能量在第2次迭代就开始增加，影响结合2种投影算子后的模型的平滑能力，使得结合2种投影算子后的算法无法收敛到较好的效果。

根据裂缝的灰度特征，裂缝邻域均值较小，而非裂缝区域邻域均值较大。受双边滤波器[10]的启发，本文在考虑邻域微分几何空间的同时，结合邻域内相邻像素的灰度值差距，修正正则化能量。且正则化能量在第2次开始时是增加的，通过曲率正则化能量与邻域像素作差以适应裂缝图像的特征，提出一个新的正则能量项，如式(3)所示:

(3)

其中，K(U)为曲率正则化能量，Ψ=(y,U)表示几何曲面，y为空间坐标，|gm|为8邻域灰度值均值。

修正后的能量函数曲线如图5b所示，正则化能量和总能量在多次迭代后可收敛至较平稳的结果，证明了本文方法的有效性。改进的曲率滤波结果如图6d所示。通过改进曲率滤波滤除了干扰，并且可以保留裂缝信息，可通过图7b进一步得到验证，表明本文方法可减少图像纹理像素灰度值变化，且不会显著影响裂缝像素的灰度值。

3.2 二次分割裂缝提取

裂缝是空间上聚集灰度相似的像素点的集合，经改进的曲率滤波平滑图像后，可通过阈值分割提取路面裂缝。本文采用子块分析方法，利用二次分割的策略提取疑似裂缝。

(1)基于直方图拟合的粗分割。

粗分割大致定位裂缝的灰度区间及可能的分布区域。由裂缝的灰度特征，裂缝像素主要分布在灰度直方图左侧的一小部分区域内，可以利用直方图拟合的方法粗分割。

首先，将经改进曲率滤波后的图像划分为互不重叠的256×256像素的子块图像。其次，以子块为单元，利用迭代式阈值分割算法[11]计算子块图像的灰度阈值iimg，在直方图上选取灰度值小于iimg的区间。然后,利用高斯函数G(μ,s2)拟合位于最大值左侧的直方图区间(其中,μ和s2分别表示最大值左侧直方图的均值和方差),计算阈值Th，使P(Th)分别为65.39%,95.4%,99.7%，其对应Th=μ-s,Th=μ-2s,Th=μ-3s。最后，将灰度值小于Th的像素标记为“1”(裂缝像素)，其余标记为“0”(非裂缝像素)，完成图像所有子块分割。通过实验采用不同阈值对3 050幅裂缝图像进行检测，其漏检率和误检率如表1所示。

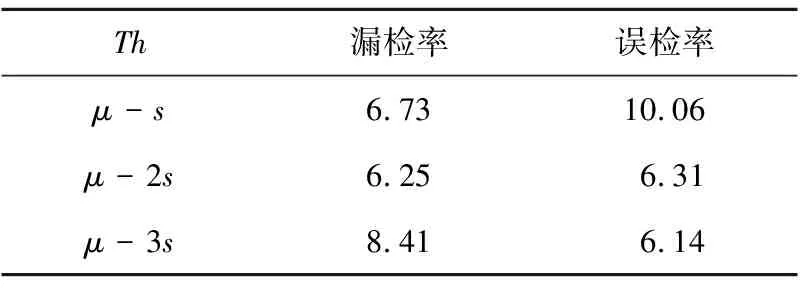
Table 1 Influence of different values of threshold on detection results

考虑漏检率应尽可能小，而误检率应尽可能大，本文选取Th=μ-2s。图8c是图8b一子块灰度值小于iimg的区间，黑点为高斯函数均值μ(125)，均值左侧曲线表示拟合的高斯函数，计算出的阈值为Th=91。阈值分割的结果如图8d所示。去除离心率不满足要求的连通域，得到ROI，如图8e所示，后续根据ROI对子块进行分类并计算子块图像的二次分割阈值，因此提取的ROI必须准确可靠。

(2)子块图像自适应分类及细分割。

细分割进一步提取疑似裂缝。本文对含有ROI的子块采用直方图估计[12]的方法计算阈值，按不同阈值将子块分为6类，如图8f所示。比较非ROI子块与已知类别子块灰度均值、方差的相似性，将其归为最为接近的那一类，实现所有子块图像的分类，如图8g所示。将子块分成若干类别，同时获得每一类别的分割阈值，按照此分割阈值对子块二次分割得到最终提取的裂缝，提取结果如图8h所示。经二次分割，裂缝区域显著增多。

3.3 裂缝噪声自适应去除

经过裂缝提取后，裂缝主体已被识别出来，但存在大量的块状或点状噪声。噪声产生的主要原因是部分小尺度纹理与裂缝的灰度区间相似，且纹理像素的坐标分布不连续，而文中的粗分割方法是基于直方图的，对目标的空间信息不敏感，会将这些噪声错误地识别为裂缝，这种情况下可根据裂缝表现出的几何特征将二者区分开。Tong等[13-15]分别利用连通域的长宽比、离心率和面积率，通过设定经验阈值来区分裂缝与噪声的方法，都取得了较好的效果，但阈值的确定存在一定的主观性。本文采用K-means算法对目标的块状或点状噪声进行自适应分类，而不依赖于特征因子的阈值。特征因子连通域的长宽比、离心率和面积率的定义如下所示：

定义1长宽比L-Wratio是指最小外接矩形的长L与宽W的比值，如式(4)所示。该比值反映裂缝的线状特征,其值越大，说明连通域是裂缝的可能性越大。

(4)

定义2离心率e是指与连通域具有相同标准二阶中心矩的椭圆的2个焦点间的距离c和长轴长度a的比值，如式(5)所示。该值反映了裂缝的线状特征，其值越大，表明该连通域越接近于直线，是裂缝的可能性越大。

(5)

定义3面积率Sratio是指连通域的面积bwarea与最小外接矩面积的比值，如式(6)所示。Sratio越小，表明该连通域的线性特征越明显，是裂缝的可能性越大。

(6)

聚类是一种无监督学习的方法，其原理是把数据集合中相似的对象分成不同的组别或者更多的子集，使在同一个子集中的成员都具有相似的属性。裂缝连通域包含裂缝和噪声2类，设定K-means算法中的类别数K=2，特征向量由3个特征因子构成，即X=(L-Wratio,e,Sratio)。图8h的聚类结果如图9所示，其中第1类表示噪声，第2类表示裂缝。去除噪声的结果如图10所示，至此实现了裂缝的定位。

4 裂缝片段连接

受裂缝壁脱落、积灰等因素影响，裂缝仅在宏观上呈现连续性，去除裂缝噪声后得到的是裂缝的零碎片段，是不完整、不连续的裂缝，需要将裂缝片段的端点连接起来，以获得较完整、连续的裂缝。并且并非所有裂缝片段的端点都需要连接，因此在连接过程中需要对所有片段进行判断。

传统的判断方法通常采用贝叶斯准则进行判断，该准则以先验概率和损失函数为已知条件。对于如雷达信号的检测，雷达信号的先验概率是变化的且先验概率的获取十分困难，也无法对各种判断结果给定损失函数。为此，本文采用奈曼皮尔逊(Neyman-Pearson)准则[16]，简称N-P准则。N-P判断规则如式(7)所示：

(7)

其中，λ为检测门限。可以连接的全体连通域对lla,b组成的类别为c1类，不能连接的全体连通域对lla,b组成的类别为c2类。a,b∈{1，…，n}为连通域的索引，n为二进制图像中连通域的数量。X表示某连通域对，p(X∣c1)表示连通域对X在可以连接的条件下的连接概率密度函数。

在裂缝片段连接过程中，实际裂缝片段不能连接但错误判断为可以连接的概率为虚警概率PF。N-P准则在给定PF的条件下，使得漏检概率PM最小，即使得实际裂缝片段连接，判断结果为不连接的错误判断概率最小。本文融合位置和方向特性，得到2个特征因子，基于N-P准则对所有裂缝片段进行判断，在判断为连接的基础上进行端点连接。具体步骤如下所示：

步骤1对所有连通域进行评估，考虑连通域的空间位置和方向特征得到2个特征因子x1a,b和x2a,b。(1)x1a,b：表示连通域a和b之间的最短距离。x1a,b指区域的位置特征，依据相邻相似的原则，连通域在空间位置上距离越近,属于同一裂缝的可能性就越大。(2)x2a,b表示连通域a和b具有相同标准二阶中心矩的椭圆的长轴方向之间的最小角度。本文将与连通域具有相同标准二阶中心矩的椭圆的长轴方向作为连通域的方向，x2a,b越小，裂缝的相似度越高。此时将连通域对X表示为向量形式，如式(8)所示：

(8)

步骤2假设每个随机变量x1a,b,x2a,b都分别服从高斯分布且相互独立，即N1(u1,σ1)，N2(u2,σ2),其中，u1和u2分别表示随机变量x1a,b和x2a,b的均值，σ1和σ2分别表示随机变量x1a,b和x2a,b的方差，则随机变量x1a,b与x2a,b的二维均值向量和协方差矩阵分别如式(9)所示：

(9)

其中,ω∈{1,2}是类别。

步骤3根据全概率公式、正态分布的概率密度函数公式，利用式(8)和式(9)对式(7)进行推导，得到式(10)。当式(10)成立时，可将2个连通域中最近的端点连接起来。

(10)

其中，m∈{1,2}是随机变量的维数。

经过上述步骤进行连接判断及端点连接，最终实现裂缝识别。图11a和图11c为经裂缝噪声去除后的效果图，图11b和图11d分别展示的是图11a和图11c经裂缝片段连接的效果，如图11a矩形框中的a1～a6、图11c矩形框中的c1～c4经连接后，分别对应图11b矩形框中的b1～b6、图11d矩形框中的d1～d4。可以看出，本文裂缝片段连接方法能有效连接断裂的裂缝。

5 实验与结果分析

5.1 有效性验证

本节利用公开数据集[17]，对现有较好的裂缝检测方法Kittler法[18]、大津法[19]、松弛因子法[20]以及本文方法进行对比实验，从测试效果和裂缝识别的完整性2个方面对实验结果进行对比分析。图12a第1列从上至下分别代表连续性差的横缝、低对比度的纵缝、高对比度的纵缝及光照不均匀的网状裂缝图像。从图12可知，本文方法与现有其它方法相比，对于漏检、局部不连续等状况有明显的改善，且检测出的裂缝清晰完整，与人工描点的裂缝较吻合，其检测结果明显优于其它方法。

本文使用机器学习中常用的精确率P(Precision)、召回率R(Recall)以及F值[14]进行完整性评估，各指标的定义如式(11)所示:

(11)

其中，TP表示真阳性,FP表示假阳性,FN表示假阴性。通过式(11)可得误检率(1-P)和漏检率(1-R)。将不同方法的识别结果与人工描点进行比对，得到裂缝完整性评估结果，如图13所示，本文方法的P、R、F均高于其他3种方法的。

5.2 工程数据分析

本文还对道路检测装备采集的工程数据进行了实验。图14a第1列从上至下分别代表横裂、纵裂、块裂及龟裂缝图像，各行表示对于不同裂缝图像，本文方法的各步骤图及人工描点图。

具体分析如下：

(1)对第3.1节中的曲率滤波方法与改进的曲率滤波方法的平滑度进行测试，结果如图15所示。改进的高斯曲率滤波方法的P、R指标均高于曲率滤波的，分别提高了5.6%,9.4%。

(2)对第3.2节中所示粗分割和二次分割结果进行评估，评估结果如图16所示。经过第二次分割后，评估指标F值提高了8.7%。

(3)对第3.3节中的裂缝噪声去除，分别利用长宽比[13]、离心率[14]和面积率[15]，通过设置经验阈值的方法，与本文方法进行对比实验，评估结果如图17所示。采用本文方法对裂缝噪声消除最好，误检率分别降低了44.1%，34.5%和61.2%，漏检率分别降低了78.1%，76.5%和79.3%。

(4)裂缝片段连接的判断过程中，需要设置λ，从而获得虚警概率PF与检测概率PD=1-PM。设λ的值在[3.5,5.5]，以0.1为步长计算PF，部分结果如表2所示。绘制受试工作特性曲线如图18所示，计算坐标点(0,1)到曲线最近距离对应的坐标A(0.0320，0.9394)，即PF=0.0320，根据表2查出，此时λ为5.0，检测概率PD为0.939 4。

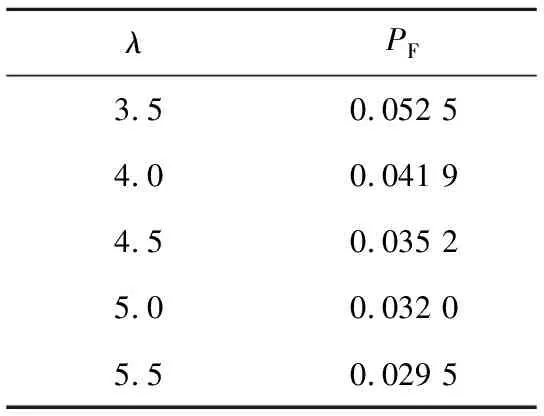
Table 2 Correspondence between λ and PF

(5)利用工程数据中的裂缝图像分别对第3.3节(连接前)与第4节(连接后)测试裂缝识别的完整性，连接前P、R和F值分别为81.1%,79.8%和80.4%，连接后P、R和F值分别为91.2%,90.2%和90.7%，P、R、F值分别提高了12.5%，13.1%和12.8%。相比本文提出的滤波、分割方法，本文提出的连接方法对裂缝的完整性检测起到了至关重要的作用。

6 结束语

本文提出了一种基于曲率滤波与N-P准则的路面裂缝识别方法，通过组合最小矩形切平面和最小三角形切平面及修正正则化能量的改进曲率滤波算法，达到了消除随机噪声、平滑路面纹理噪声和裂缝保留的目的。以子块为单元，利用裂缝灰度特征采取二次分割的策略提取疑似裂缝目标集合，运用裂缝几何特性自适应去除块状或点状噪声，进而获得裂缝片段和实现裂缝的定位。在此基础上，融合裂缝片段的位置和方向信息，基于N-P准则连接裂缝片段端点，实现裂缝的完整性检测。与其它裂缝检测方法比较，本文方法可以对不同特征、位置的裂缝目标进行有效检测，具有更好的检测效果和更高的检测精度。

本文研究建立在裂缝与背景灰度形成差异的基础上，对于裂缝与纹理灰度相似的裂缝的检测具有局限性。未来将结合裂缝灰度及脊边缘特征的不同优点，在裂缝多特征融合方面展开深入研究，进一步提高识别的准确性。