三维空间智能弹药集群协同攻击

■ 张磊 杨帆

1 引言

山地或海岛作战时，需要对反斜面目标进行突防、打击及压制，本文以此为背景，研究智能弹药集群对目标的协同攻击问题。智能弹药具备察打一体、快速智能打击等特点，对反斜面目标的攻击具有一定的自主性，智能弹药集群作战可在战场局部区域对特定目标形成“协同饱和攻击”态势，更具压制优势。智能弹药集群攻击目标时，若无法保证同时攻击目标，后续弹药会受到火光、烟雾等影响，造成目标打击精度的降低，集群毁伤效能大大降低，因此，协同攻击时间是智能弹药集群目标攻击作战问题的关键。张友安通过将时间控制问题转化为弹目距离问题，提出了一种基于时间约束的协同导引律，实现多枚导弹对目标的同时攻击。

本文以某基地静止（或低速）目标为研究对象，针对智能弹药集群攻击目标的关键问题，提出一种基于协同攻击时间约束的变结构控制导引方法，以协同集群中智能弹药的攻击时间，解决智能弹药集群执行任务时因攻击时间不一致而造成的毁伤效能降低的问题。

2 模型建立

根据作战背景，在三维空间建立单枚智能弹药与静止目标的相对运动模型，O-为地面坐标系，m-XYZ为视线坐标系，见图2.1。

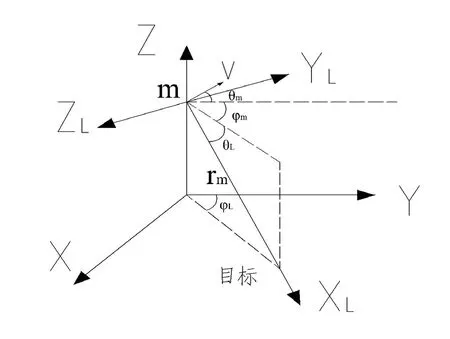
图2.1 相对运动模型

图中： r—智能弹药与静止目标的视线距离；—视线俯仰角；—视线偏航角；—智能弹药俯仰角；—智能弹药偏航角；—智能弹药飞行速度。根据相对运动模型，建立智能弹药与静止目标的运动方程为：

3 导引律设计

分别对式（2.2）、（2.3）两边对时间进行求倒，并与式（2.4）、（2.5）相结合，整理可得：

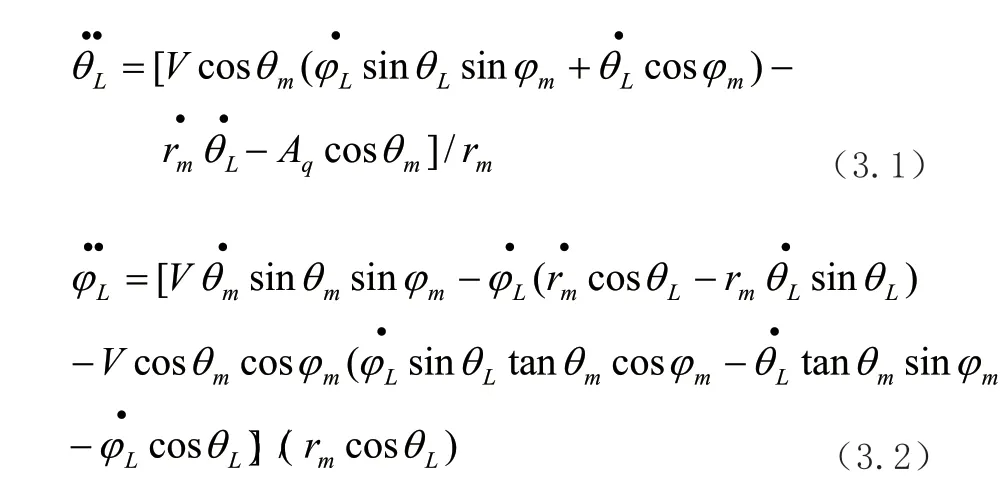
根据单枚智能弹药导引过程要求，智能弹药命中目标瞬间，其末端视线俯仰角和偏航角速率为零，即：

式中，—智能弹药命中目标时间。

智能弹药集群攻击目标时，为有效突破目标防御体系，集群中各弹药的攻击角度应尽可能分散化，本文在俯仰平面内对视线俯仰角进行约束，不同弹药施以不同攻击角度的约束，实现智能弹药集群以分散化攻击角度命中目标，即：

智能弹药集群实现对目标的协同攻击的必要前提，在于攻击过程中各智能弹药的剩余导引时间应逐渐收敛并保持一致，因此，设定期望协同攻击时间为。本文将各智能弹药剩余导引时间的控制转化为实际导引时间与期望协同攻击时间误差的控制，智能弹药命中目标瞬间，要求在其俯仰平面和偏航平面内时间误差收敛于零，即：

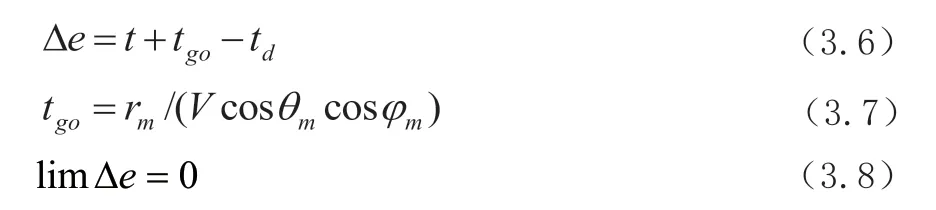
式中，Δ—时间误差；t—智能弹药瞬时剩余导引时间。

弹药集群协同攻击目标背景下，需要的导引规律需具有鲁棒性强、自适应等特点，经典导引规律很难满足导引需求。本文设计滑动模态变结构控制导引方法协同智能弹药集群的目标攻击，其优点在于设计简单，且具有很强的鲁棒性及自适应性。

对于单枚智能弹药，基于视线角速率及导引时间误差两种变量，分别在俯仰平面和偏航平面内选取滑模面为：

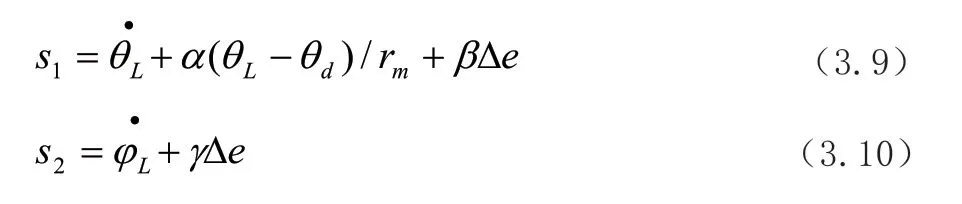
式中：—视线俯仰角误差系数，且＞0；—俯仰平面时间误差系数，且＞0；—偏航平面时间误差系数，且＞0。

此时，智能弹药导引系统处于滑模运动状态，智能弹药可按期望视线俯仰角和期望协同攻击时间命中目标。由于自适应滑模趋近律在智能弹药导引的不同时刻趋近滑模的速率可以自适应变化的特性，保证智能弹药协同攻击时间和攻击角度的精度，选取自适应滑模趋近律为：

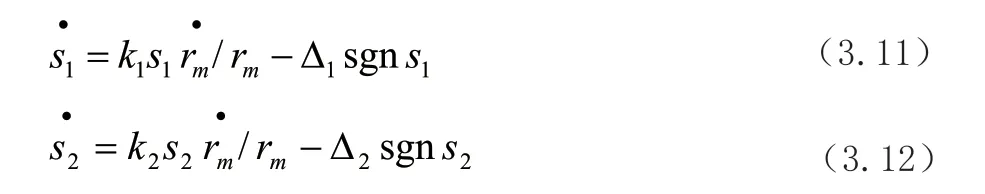
其中，，，Δ，Δ为大于零的常数。

分别将式（3.9）、（3.10）两边对时间求导，并结合式（3.1）、（3.2），整理可得：

4 仿真实验

基于本文设计的攻击时间约束滑模变结构控制导引方法，使用Matlab 进行5 枚智能弹药协同攻击目标的三维仿真验证。假设目标空间位置为（2500m，3500m，0m），智能弹药飞行速度均为30m/s，初始飞行高度在100～200 米，初始俯仰角（弹道倾角）为0°，仿真步长0.01s，其他基本参数初始化见表4.1。

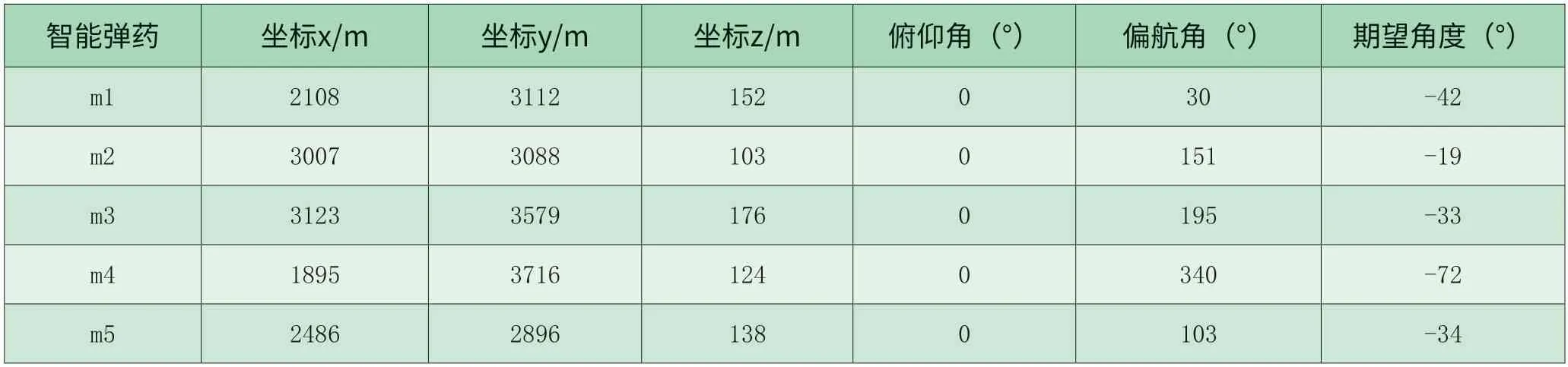
表4.1 智能弹药参数初始化

4.1 智能弹药无协同攻击时间约束下的攻击仿真

在无协同攻击时间约束条件下，智能弹药攻击目标过程中的导引方法不包含时间误差控制项，各智能弹药以最短时间将俯仰角收敛于期望角度，并保持该期望角度攻击目标。

仿真弹迹曲线见图4.1，5 枚智能弹药在无协同攻击时间约束条件下对目标进行攻击，可以看出，在无时间误差控制项的导引方法控制下，各智能弹药快速调整其运动方向，使其俯仰角以尽可能短的时间收敛于期望角度，后以近乎直线的弹迹命中目标。智能弹药攻击时间及脱靶量数据见表4.2，此时弹药的攻击时间为最短攻击时间，集群中各弹药的攻击时间在19.52s～21.59s，时间差异明显。

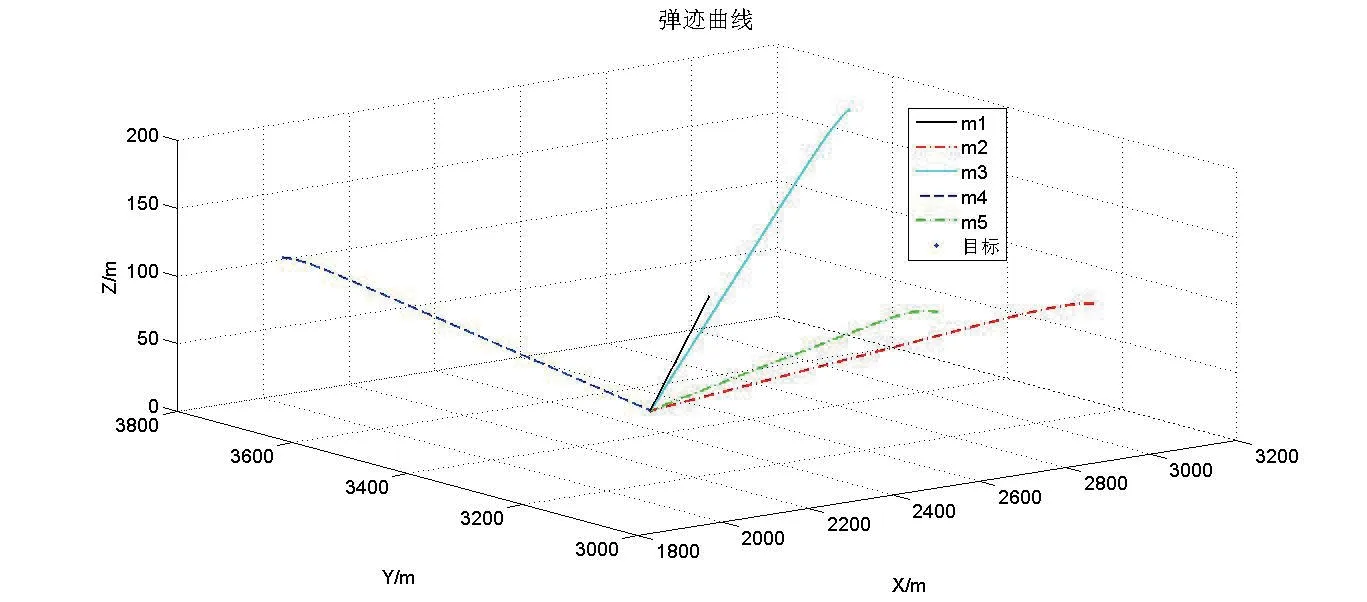
图4.1 智能弹药无协同攻击时间约束下弹迹曲线

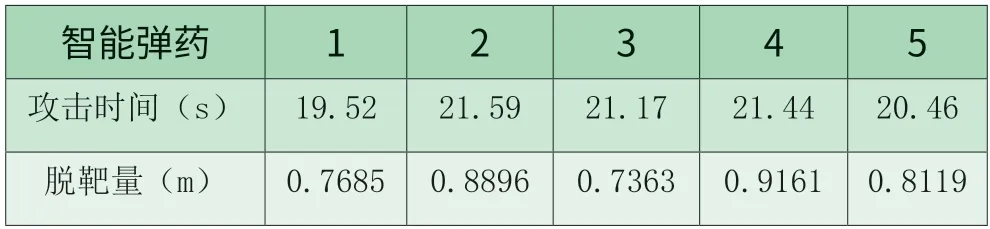
表4.2 智能弹药无协同攻击时间约束下攻击效果

4.2 智能弹药协同攻击时间约束下的攻击仿真

在协同攻击时间约束条件下，智能弹药攻击目标过程中的导引方法包含时间误差控制项，弹药攻击过程中同时保证俯仰角收敛于期望角度、时间误差收敛于零。根据4.1 节的仿真结果，可知智能弹药攻击用时最长为21.59s，若实现集群中各弹药同时攻击目标的效果，期望协同攻击时间必须大于攻击用时最长时间，因此，本文选取3 个期望协同攻击时间（22.0s、26.0s 和30.0s）进行仿真。

3个不同期望协同攻击时间下的仿真弹迹曲线见图4.2，与无协同攻击时间约束时相比，基于协同攻击时间约束的弹迹曲线弯曲程度明显大于无约束状态；不同协同攻击时间相比，期望时间越长弹迹曲线越弯曲。可以发现，基于协同攻击时间的滑模变结构控制导引方法通过控制智能弹药增大弹迹曲线的弯曲程度来延长并协调弹药的攻击时间。

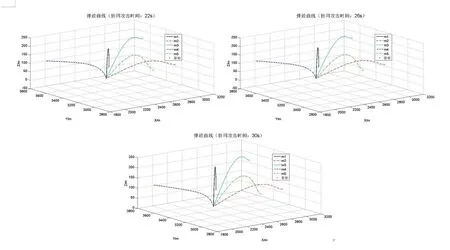
图4.2 智能弹药协同攻击弹迹曲线

智能弹药集群协同攻击时间及脱靶量见表4.3，基于协同攻击时间约束的智能弹药攻击目标时间均收敛于期望攻击时间，本文设计的导引方法具有很好的时间协同性，实际攻击时间与期望攻击时间的误差小于0.03s，智能弹药集群获得了较好的协同攻击效果。

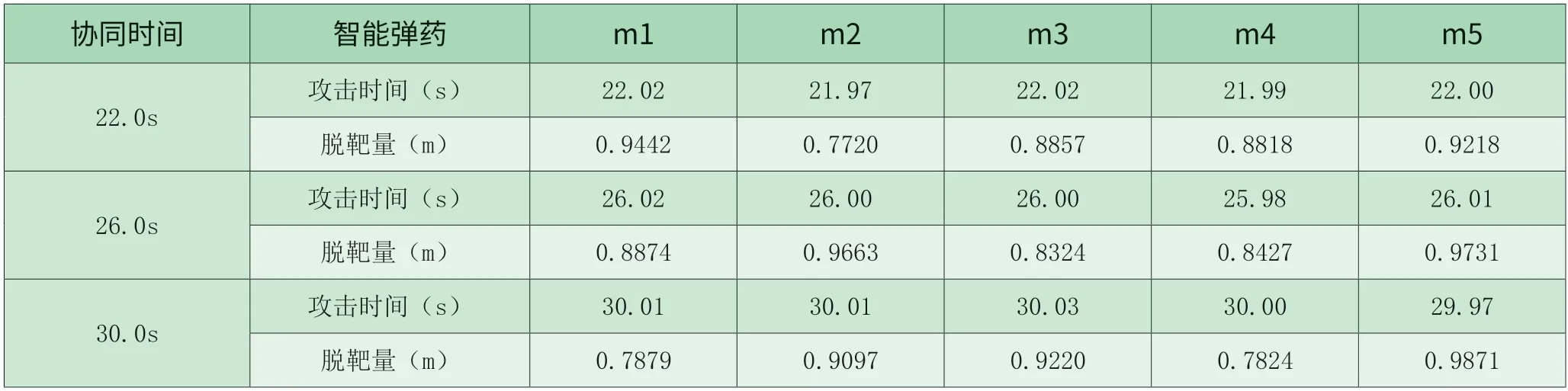
表4.3 智能弹药协同攻击时间约束下攻击效果

智能弹药在不同期望攻击时间下其攻击过程角度与时间的对应关系见图4.3，可以发现，期望协同攻击时间越长，智能弹药视线俯仰角调整幅度越大，其弹迹曲线越弯曲，其攻击角度收敛于期望角度的时间也越长，进一步证明了基于协同攻击时间约束下滑模变结构导引方法通过控制智能弹药的俯仰角度大小以实现攻击时间的协同。

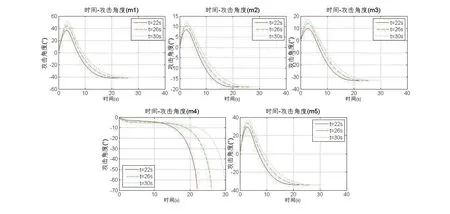
图4.3 智能弹药不同期望攻击时间约束下攻击角度与时间对比关系

5 结论

本文研究了智能弹药集群在三维空间下攻击静止目标的攻击时间协同问题，对三维空间下弹目运动关系进行建模，并建立弹目运动方程，从视线角和剩余时间两方面入手研究，提出基于协同攻击时间约束的滑模变结构控制导引方法。通过仿真实现了5 枚智能弹药以特定攻击角度协同攻击目标，协同攻击时间效果较好。