某自行高炮刚柔耦合动力学建模方法研究
2022-10-27张鑫张辉王宝宝贺世豪
张鑫,张辉,王宝宝,贺世豪
(1.中国船舶重工集团公司第七一六研究所,江苏 连云港 222000;2.南京理工大学 机械工程学院,江苏 南京 210094)
小口径自行高炮在射击过程中,车体在三维空间上会产生刚体位移和弹性变形[1-3]。车体作为武器系统的安装平台,其姿态变化会间接造成身管指向发生改变,引起弹丸出炮口时的扰动增大,从而对自行高炮的射击精度产生很大影响[4-5]。为了确保自行高炮的射击精度,需要准确、实时地获取射击过程中的车体姿态信息,以满足火控系统的需要。火控系统根据当前的车体姿态信息对跟踪和解相遇问题进行相应的修正计算[6-8]。
传统的车体姿态获取手段主要有结构动力学仿真、多体动力学计算和传感器测量等方法。梁传建等[9]通过构建某自行火炮火力部分的非线性有限元动力学模型,对火炮射击时座圈的动态响应开展了研究。孟凡东等[10]通过建模分析和仿真计算,量化了自行高炮车体姿态测量误差对射击诸元的影响。寇超等[11]设计了自行高炮模拟仿真实验平台,能够实时模拟车体姿态变化,开展行进间射击和急停急射训练模拟。笔者以某自行高炮为研究对象,对其进行了刚柔耦合建模方法研究。
1 某自行高炮结构分析
1.1 基本假设
为了减少模型规模,对自行高炮进行如下假设:
1)除车架考虑为柔性体之外,其余构件均视为刚体;
2)忽略构件之间的间隙、碰撞等结构非线性因素;
3)忽略各个构件的结构阻尼;
4)不考虑射击过程中弹丸和身管之间的耦合作用;
5)忽略射击过程中后坐部分运动造成的质量、质心变化。
1.2 拓扑模型
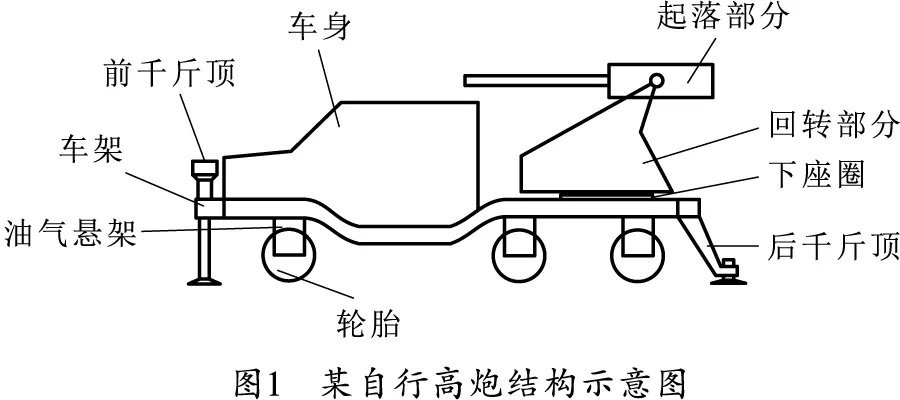
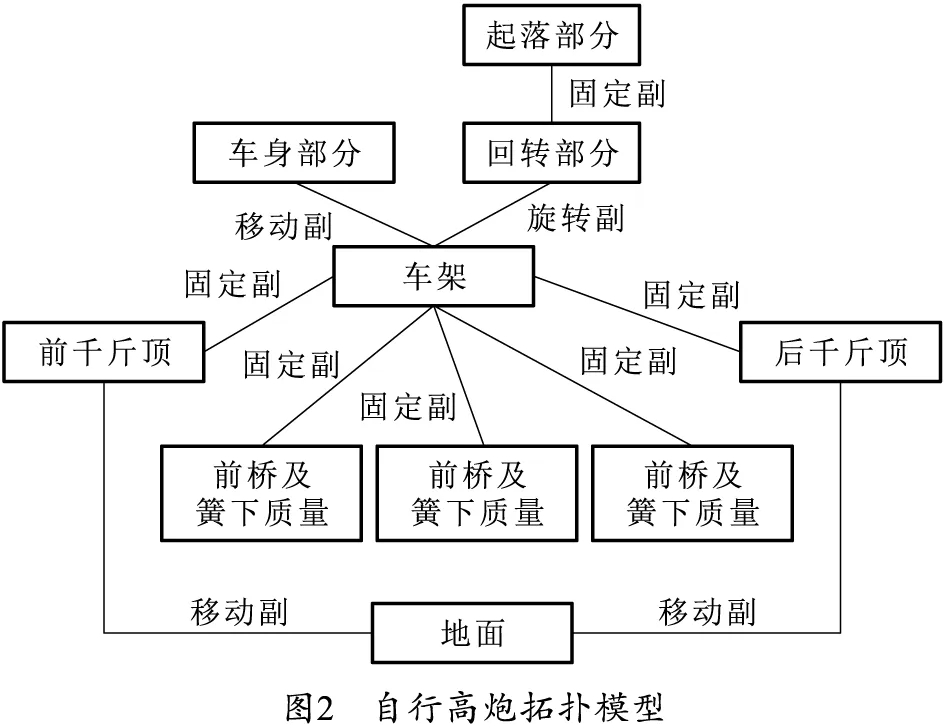
某轮式自行高炮结构示意图如图1所示,底盘型号为6×6,悬架类型为独立油气悬架。火炮射击时,车身及车架由4个千斤顶完全撑起,摇架承受的后坐力经由耳轴及高低传动机构传递到托架,最后通过座圈传递到车体,造成下座圈及车体的位姿变化。车架的振动造成车身连接处橡胶垫的弹性变形,从而引起车身的位姿变化。拓扑结构如图2所示。
1.3 参考坐标系定义
自行高炮是一个复杂的机械系统,为了更好地描述各构件的运动状态,对构件进行受力分析。自行高炮为小阻尼系统,因此在动力学模型的构建过程中对阻尼作用进行了省略。
自行高炮简化结构如图3所示。
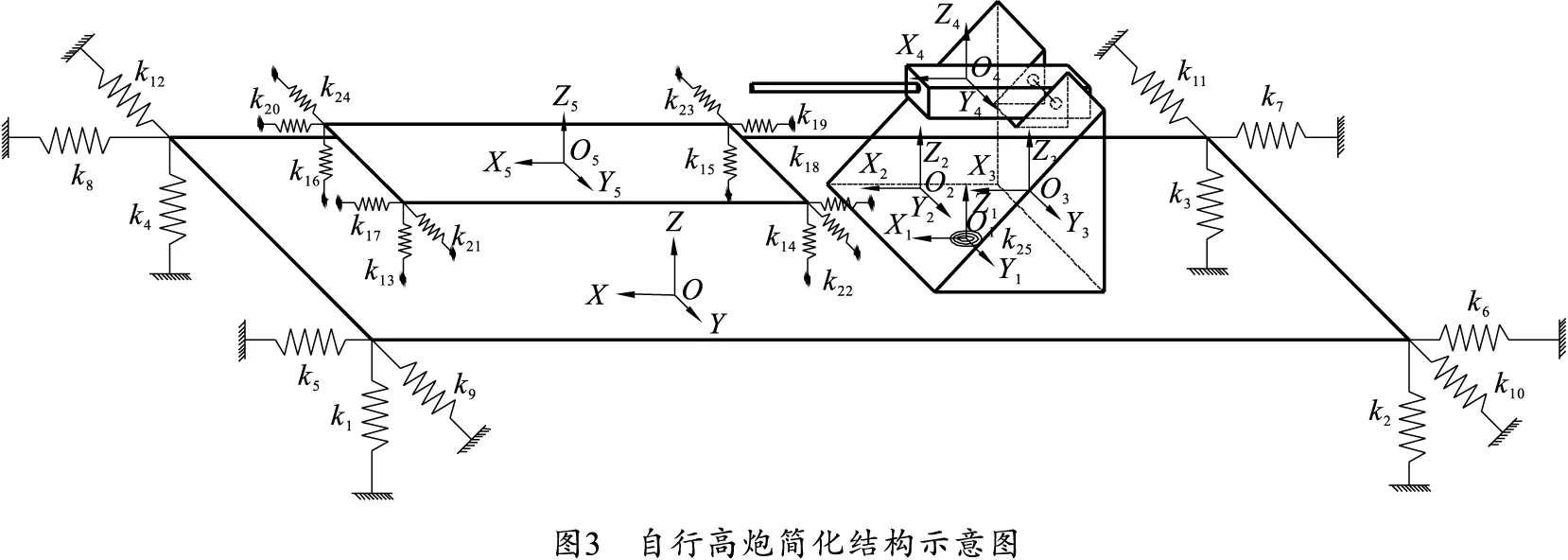
图3中k1、k2、k3、k4为千斤顶垂向等效弹性系数;k5、k6、k7、k8为千斤顶前后方向等效弹性系数;k9、k10、k11、k12为千斤顶左右方向等效弹性系数;k13、k14、k15、k16为橡胶垫块垂向等效弹性系数;k17、k18、k19、k20为橡胶垫块前后方向等效弹性系数;k21、k22、k23、k24为橡胶垫块左右方向等效弹性系数;k25为方向机等效扭簧弹性系数。
现对不同原点的惯性坐标系及各构件连体坐标系进行定义,各坐标系定义如下:
1)惯性坐标系N或OXYZ:惯性坐标系N固结于大地,不随车辆位置的变化而改变,主要用来描述车辆的空间位置、速度以及加速度等状态参量,其原点O与车架的质心重合;X轴沿着车辆初始的纵向方向,向前为正;Z轴与重力方向相反,向上为正;Y轴垂直于XOZ平面且方向符合右手定则。
2)下座圈坐标系N1或O1X1Y1Z1:惯性坐标系N1固结于大地,不随高炮位姿的变化而改变,主要用来描述起落部分和回转部分的空间位置、速度以及加速度等状态参量,其原点O1与下座圈的几何中心点重合;X1轴沿着车辆初始的纵向方向,向前为正;Z1轴与重力方向相反,向上为正;Y1轴垂直于X1O1Z1平面且方向符合右手定则。
3)上装部分坐标系N2或O2X2Y2Z2:起落部分坐标系是固结于上装部分质心且不随高炮位姿的变化而改变的惯性坐标系,主要用来求解不同射角下上装部分的惯性张量,其原点O2与上装部分的质心重合,X2轴沿着车辆初始的纵向方向,向前为正;Z2轴与重力方向相反,向上为正;Y2轴垂直于X2O2Z2平面且方向符合右手定则。
4)回转部分坐标系G1或O3X3Y3Z3:回转部分坐标系是固结于回转部分质心且随回转部分位姿变化而改变的随体坐标系,主要用来描述回转部分的运动状态,其原点O3与回转部分质心重合;X3轴沿着回转部分的正面方向,向前为正;Z3轴与重力方向相反,向上为正;Y3轴垂直于X3O3Z3平面且方向符合右手定则。
5)起落部分坐标系G2或O4X4Y4Z4:起落部分坐标系是固结于起落部分质心且随起落部分位姿变化而改变的随体坐标系,主要用来描述起落部分的运动状态,其原点O4与起落部分的质心重合;X4轴沿着身管指向,向前为正;Y4轴指向回转部分侧面方向,向左为正;Z4轴垂直于X4O4Y4平面且方向符合右手定则。
6)车身坐标系G3或O5X5Y5Z5:车身坐标系是固结于车身且随车身位置变化而改变的随体坐标系,主要用来描述车身的运动状态,其原点O5与车身的质量中心重合;X5轴沿着车身的纵向方向,向前为正;Z5轴与重力方向相反,向上为正;Y5轴垂直于X5O5Z5平面且方向符合右手定则。
2 某自行高炮刚柔耦合动力学模型
2.1 上装部分动力学建模
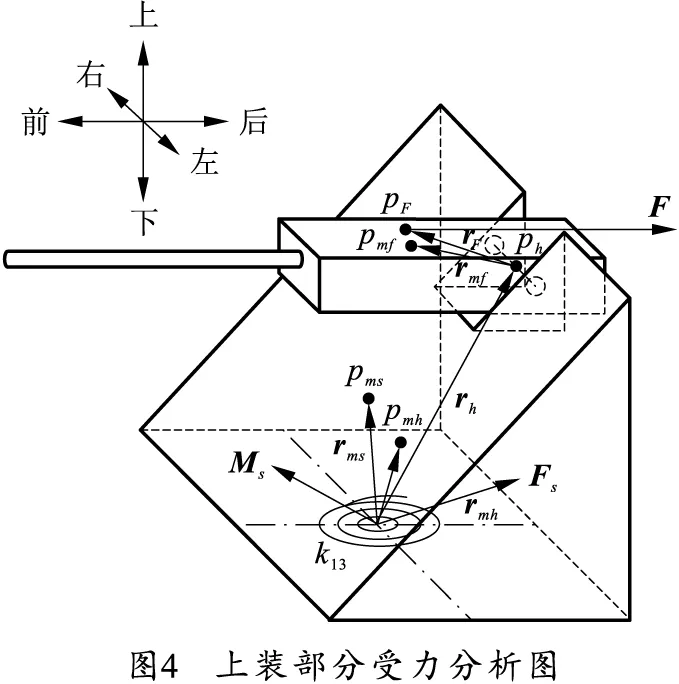
射角改变时,上装部分的质心位置和惯性张量、后坐力的指向和作用点也会随之变化,在惯性坐标系下对任意射角下的自行高炮载荷进行分析。上装部分受力分析及符号规定如图4所示。
车架对上装部分的约束力和约束反力矩分别为Fs和Ms。ph为耳轴回转中心点,rh为ph在下座圈坐标系N1下的空间坐标向量;pF为后坐力作用点,rF为pF在起落坐标系G2下的空间坐标向量;pms为上装部分质心点,rms为pms在下座圈坐标系N1下的空间坐标向量;pmh为回转部分质心点,rmh为pmh在回转坐标系G1下的空间坐标向量;pmf为起落部分质心点,rmf为pmf在起落坐标系G2下的空间坐标向量。
将起落部分和回转部分的质量信息由各自的随动坐标系转化到惯性坐标系下,在惯性坐标系下对上装部分进行动力学分析。规定方位射角ψf和高低射角θf对应的坐标系转换矩阵为Aψf和Aθf。
回转部分质心在惯性坐标系N下的坐标为
(1)
起落部分质心在惯性坐标系N下的坐标为
(2)
则上装部分质心在惯性坐标系N下的坐标为
(3)
式中:mh为回转部分质量;mf为起落部分质量。
下座圈坐标系N1下后坐力作用点pF相对于上装部分质心pms的坐标为
(4)
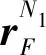
回转部分在惯性坐标系N下的惯性张量为
(5)
式中,IhG1为回转部分在G1坐标系下的转动惯量。
起落部分在惯性坐标系N下的惯性张量为
IfN=AψfAθfIfG2(AψfAθf)T,
(6)
式中,IfG2为起落部分在G2坐标系下的转动惯量。
上装部分质心的加速度计算公式为
αs=αz+βs×rms+ωs×(ωs×rms),
(7)
式中:αz为下座圈中心点加速度;βs为上装部分的角加速度;ωs为上装部分的角速度。
下座圈坐标系N1下的后坐力为
FN1=AψfAθfF,
(8)
式中,F为起落部分坐标系G2下的后坐力。
在惯性坐标系下,以上装部分质心为参考点对上装部分进行动力学分析,应用牛顿欧拉法推导出上装部分动力学方程为
FN1+Fs=(mf+mh)αs,
(9)
(10)
式中,Is为上装部分的惯性张量。
2.2 车身动力学建模
车身由车壳、发动机、电器柜和蓄电池等构件组成,这些构件没有相对运动关系,故简化为一个刚体构件。车架与车身之间通过减振橡胶垫相连接,其力学特性为三向线性弹簧。在惯性坐标系下以车身质心为参考点对其进行动力学分析,推导出射击状态下车身的动力学方程组。车身受力分析及符号规定如图5所示。
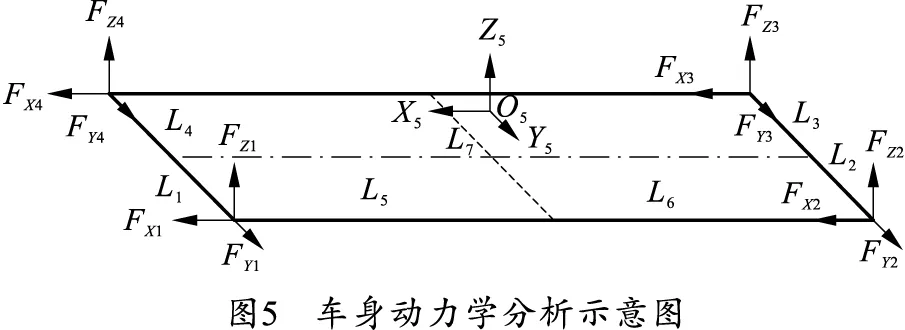
FXi、FYi、FZi分别为第i个橡胶垫块对车身X、Y、Z方向的作用力,i=1、2、3、4。L1、L2、L3、L4分别为左前、左后、右后、右前橡胶垫块与车身质心沿Y方向的距离;L5、L6分别为前橡胶垫块、后橡胶垫块与车身质心沿X方向的距离;L7为所有橡胶垫块与车身质心沿Z方向的距离。车身在射击过程中的位移为Rb=[xbybzb]T,角位移为Wb=[φbθbψb]T。前左方向橡胶垫块在惯性坐标系下相对车身质心的位置坐标为rb1=[L1L5-L7]T;后左方向橡胶垫块的位置坐标为rb2=[L2-L6-L7]T;后右方向橡胶垫块的位置坐标为rb3=[-L3-L6-L7]T;前右方向橡胶垫块的位置坐标为rb4=[-L4L5-L7]T。与第i个橡胶垫块下端连接车架点的位移为uci=[xciycizci]T。第1个橡胶垫块的刚度矩阵为K1=[k17k21k13]T;第2个橡胶垫块的刚度矩阵为K2=[k18k22k14]T;第3个橡胶垫块的刚度矩阵为K3=[k19k23k15]T;第4个橡胶垫块的刚度矩阵为K4=[k20k24k16]T。
第i个橡胶垫块的位移为
uri=Rb+rbi×Wb-uci.
(11)
第i个橡胶垫块对车身质心的作用力为
Fbi=[FXiFYiFZi]T=diag(Ki)·ur1,
(12)
式中,diag函数将橡胶垫块的刚度矩阵转化为对角矩阵的形式。
第i个橡胶垫块对车身质心的作用力矩为
Mbi=Fbi×ur1.
(13)
车身构件的动力学方程组为
(14)
(15)
式中:mb为车身质量;αb为车身构件的线加速度;βb为车身构件的角加速度;Ib为车身的惯性张量;ωb为车身的角速度。
2.3 车架动力学建模
据车架实体结构,在UG软件中对车架模型进行一定程度的简化,在ABAQUS软件中对简化车架进行有限元建模,分别对每个面进行不同材料属性定义,划分网格,连接界面耦合,构建的车架有限元模型如图6所示。
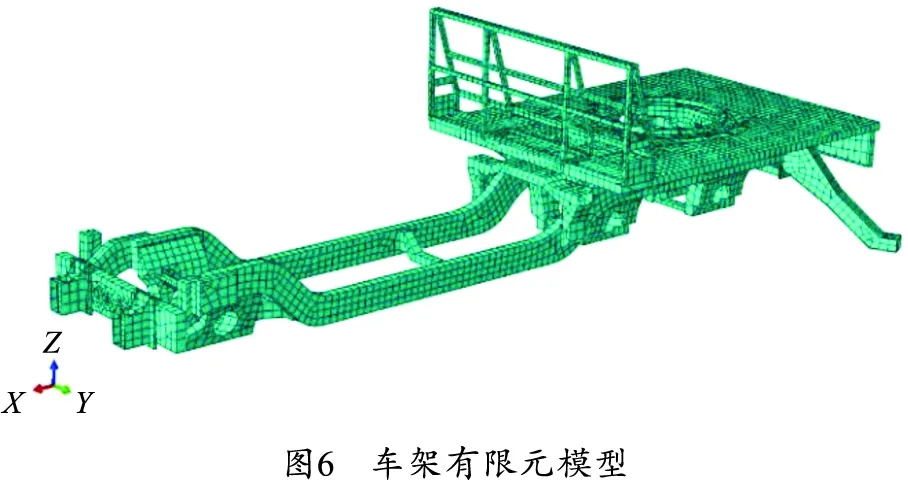
车架有限元模型共有13 276个节点和14 147个壳单元。为了便于处理刚体和柔体之间的载荷、约束或者接触关系,对连接位置的主从节点进行了定义。主从节点的定义示意图如图7所示。

主节点与从节点设置耦合关系,即主、从节点的运动关系完全一致。只有主节点和外界进行载荷、位移等信息的交换,因此主节点又被称为界面节点。图7中,RP-50、RP-77、RP-90分别耦合在车架与车桥的连接处,在界面节点处分别通过固定副将3个车桥及簧下质量与其相连。RP-137、RP-138、RP-7、RP-149分别耦合在千斤顶的上端面,在界面节点处与三向弹簧固连以模拟千斤顶的力学作用,三向弹簧的另一端固连在大地上。RP-8、RP-9、RP-10、RP-11分别耦合在车架与橡胶垫块连接处,在界面节点处与三向弹簧固连以模拟橡胶垫块的力学作用,三向弹簧的另一端与车身相连。RP-6与上座圈内径相耦合,在界面节点处与绕Z方向的扭簧相连接,另一端与上装部分总体质心相固连。
利用ABAQUS软件导出车架的质量信息与刚度信息,以便于采用直接刚度法得到自行高炮发射动力学模型。ABAQUS软件可通过更改inp文件,即在该文件增加相应的关键词即可导出质量矩阵和刚度矩阵。将生成的矩阵文件进行排序、刚度矩阵的非奇异化处理,即可得到车架柔性构件的质量矩阵和刚度矩阵。由于主从节点之间的耦合,导致车架质量矩阵和刚度矩阵的规模有一定的缩减,最终的车架动力学方程个数为76 776。
2.4 全炮发射动力学方程
对自行高炮各个构件开展动力学分析,得到了各构件的动力学方程组。为了便于系统总方程组的求解,采用直接刚度法消除方程组的约束反力及约束反力矩项,得到对称的系统总质量矩阵和总刚度矩阵,便于振型叠加法的求解。
欧拉方程中出现了上装和车架的速度平方项,根据第一阶模态频率及试验结果,推定速度平方项为高阶小量,因此省略了动力学方程中的速度平方项。
车架动力学方程如下:
(16)
车身动力学方程组经合并同类项转化为矩阵形式为
(17)
上装部分动力学方程组经合并同类项转化为矩阵形式为
(18)
前桥、中桥、后桥及相应簧下质量构成的质量矩阵分别为Mfa、Mma、Mra;4个千斤顶的刚度矩阵分别为Kfl、Krl、Krr、Kfr。
直接刚度法是将单元矩阵扩展为贡献矩阵,再叠加得到总结构刚度阵的一种方法[12]。依据车架有限元模型的界面节点编号,消除车架与上装部分、车身部分之间的约束反力项。将前桥、中桥、后桥及相应簧下质量构成的质量矩阵及4个千斤顶的刚度矩阵依据相应的界面节点编号与车架质量矩阵和刚度矩阵相结合。自行高炮系统的发射动力学模型如下:
(19)
式中:质量矩阵为

刚度矩阵为
载荷矩阵为Fg=[0 0 0 0 0 0 0 0 0 0 0Fs… 0 0]T。
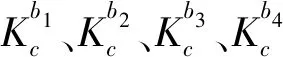
在车架质量矩阵基础上,将车身、上装、车桥及簧下质量的质量矩阵与之合并;在其刚度矩阵的基础上,将车身、上装、千斤顶的刚度矩阵与之合并。车桥及簧下质量与相应的车架界面无相对运动关系,千斤顶的连接物体是大地,故二者不会增加矩阵的规模。相对于车架的自由度而言,只增加了上装一个旋转自由度和车身六个自由度,最终的自行高炮发射动力学方程数为76 783。
3 基于振型叠加法的车体姿态求解
3.1 某自行高炮总体参数
某自行高炮动力学模型中的质量、转动惯量、刚度系数、尺寸参数设置分别如表1~4所示。

表1 质量参数表

表2 转动惯量参数表
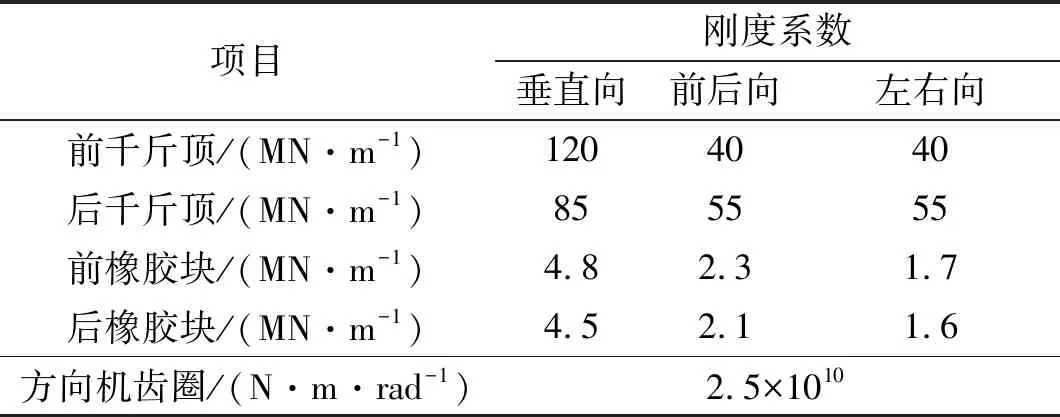
表3 刚度系数表
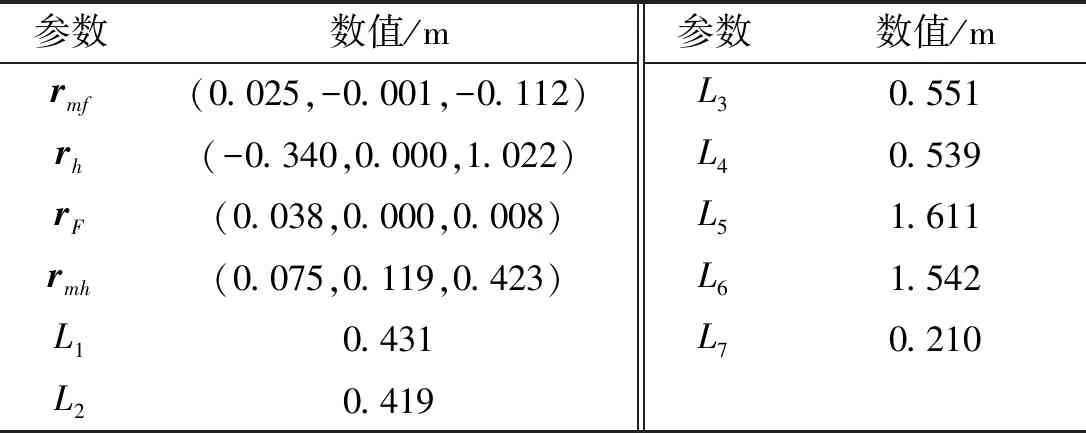
表4 各作用点空间坐标表
上述表格规定了自行高炮发射动力学模型中使用的结构参数及动力学特性参数,能够对任意射击状态下的中间变量进行计算,构造全炮刚柔耦合动力学模型,进行射击过程中的车体姿态解算。
3.2 典型工况下车体姿态求解
某自行高炮发射动力学模型是一个复杂激励作用下的76 783个耦合二阶微分方程组,由于系统的微分方程组规模过于庞大,采用振型叠加法更有利于提高求解效率。
将中间变量的解算、总质量矩阵和刚度矩阵的处理、方程组的解算等进行了编程实现,程序流程如图8所示。

对某一种试验工况进行仿真,将射击状态设置为方位射角180°,高低射角0°,射击发数7发,后坐力曲线如图9所示。
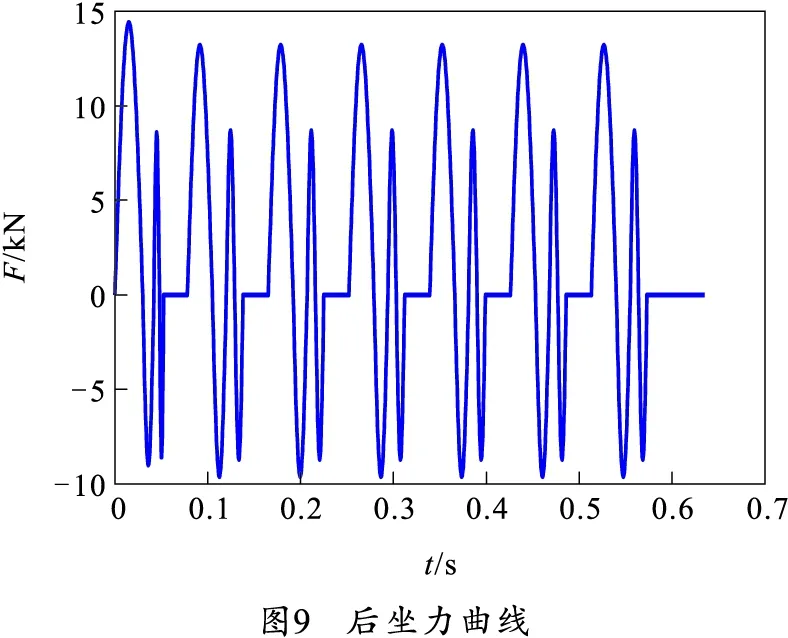
根据输入的射击状态信息,计算上装总体质心位置、质量、转动惯量、惯性积及后坐力,构造上装动力学方程组。运用直接刚度法将3个车桥的质量矩阵、4个千斤顶的刚度矩阵、上装动力学方程组、车身动力学方程组与车架动力学方程组联立,构造矩阵形式的全炮刚柔耦合动力学模型。求解系统的固有频率和固有振型,并将特征向量正则化,得到正则振型,方程组化为n个单自由度微分方程。运用Duhamel积分求解激励作用下的车体下座圈相关方程,得到正则空间下的广义位移解,将广义位移由正则空间变换到物理空间,即得到车体姿态响应。车体姿态响应如图10所示。
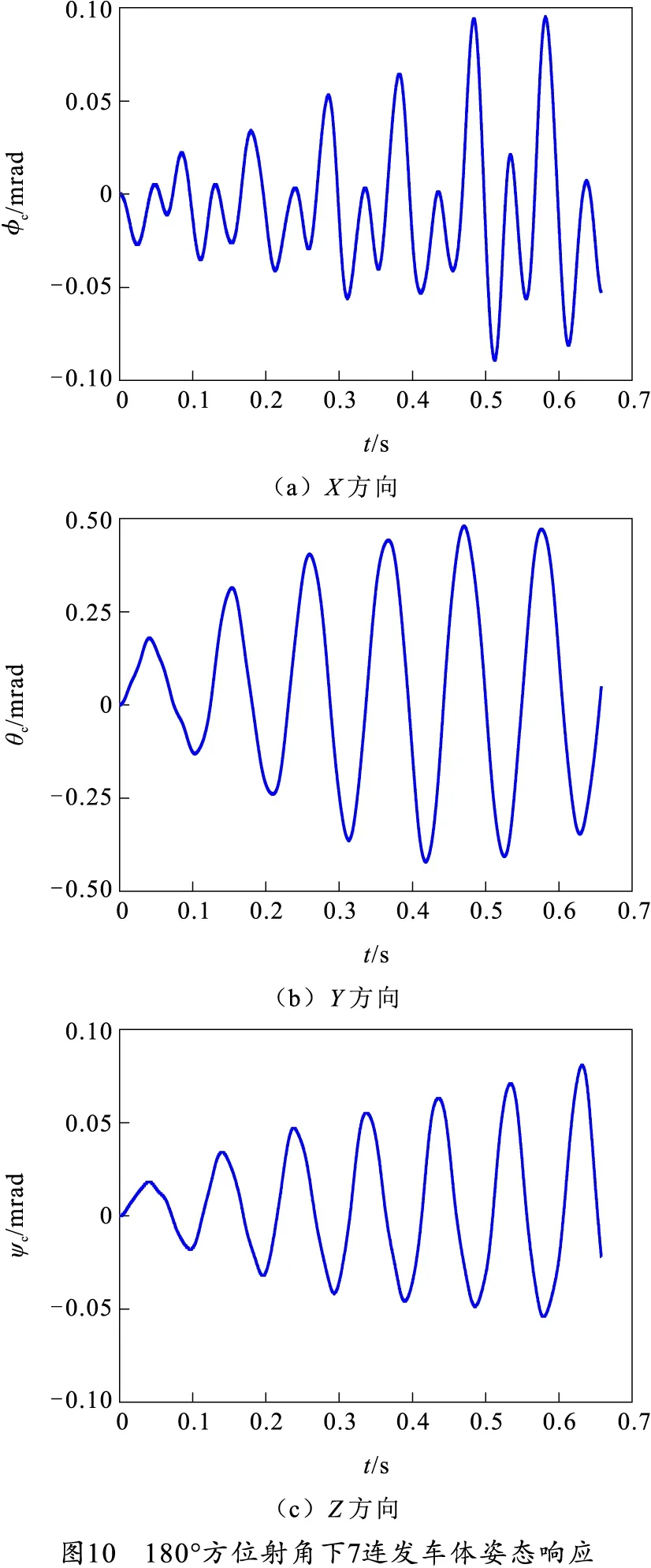
该高炮射击间隔为94 ms,运用该动力学模型解算出单发射击车体姿态响应的时间约为5 ms,而火控系统进行数据传输、火控解算的时间为10 ms,因此能够满足火控系统对车体姿态解算时间响应的要求。
Y方向的姿态幅值最大值约为0.5 mrad,X方向的姿态幅值最大值约为0.1 mrad,朝后方射击工况下,Y方向的角位移变化大于X方向是合理的。此外,3个方向的角位移幅值都逐渐增大,表明系统产生了一定程度的共振。
3.3 解算方案验证
通过ABAQUS软件和刚柔耦合模型对自行高炮进行动力学分析,振型叠加法的模态保留前15阶,提取车体下座圈的姿态响应,以验证模型解算的准确性。下座圈姿态响应结果对比如图11所示。
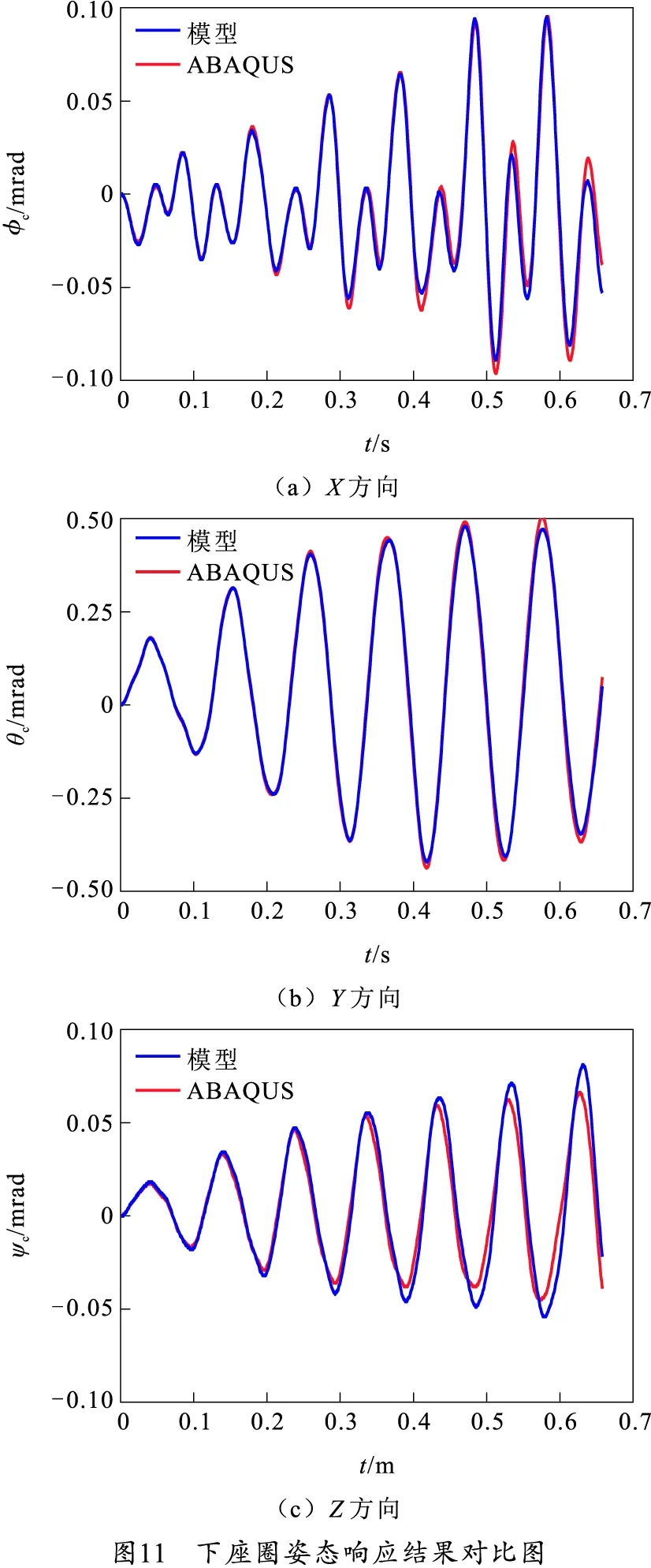
从图11可以看出,通过两种方法解算的车体姿态响应基本一致,Y方向符合的最好,X方向次之,Z方向略差。较好的符合结果表明基于刚体动力学理论和有限元法的刚柔耦合发射动力学模型构建方法具有较高的准确性,振型叠加法保留的阶次数目也设置得合理。
4 结论
以千斤顶全支撑状态下的某自行高炮为研究对象,建立了全炮刚柔耦合发射动力学模型,实现了射击过程中的车体姿态快速求解:
1)采用牛顿欧拉法分别对刚体构件进行受力分析,建立其动力学方程。
2)通过有限元法获取车架的质量矩阵、刚度矩阵,得到柔性车架构件的动力学方程。
3)采用直接刚度法消除方程组中的约束反力项,构造全炮刚柔耦合发射动力学模型。
4)振型叠加法编程实现,完成对全炮模型的动力学分析,得到射击过程中的车体姿态响应,与采用动力学仿真模型得到的姿态响应有较好的符合度。
5)该方案同时解决了多体系统的刚柔耦合建模及动力学响应快速求解两大难题,为解决复杂多体系统动力学响应快速求解问题探索了一种新方法。
