手扶式移栽机栽植机构优化设计与试验*

李慧霜，马月虹，曹新伟

(1. 新疆农业大学机电工程学院，乌鲁木齐市，830052； 2. 新疆农业科学院农业机械化研究所，乌鲁木齐市，830091)

0 引言

我国作为人口大国，对于蔬菜的需求很大，温室种植蔬菜早已成为潮流，这种种植方式可以进行气候补偿且高产稳定[1-2]。目前有一些温室依然采用最原始的人工移栽钵苗的方式进行种植，这种方式需要耗费大量的人力物力，而且移栽的效果也不是很好，比如株距不均匀、栽植深度不一致等，最重要的是在当今社会人工的费用较高，会加大蔬菜的生产成本，移栽机的出现打破传统手工移栽的局面。目前市场上已经出现了几种比较成熟的机型，比如链夹式、吊篮式、导苗管式、鸭嘴式、连杆式等[3]，但是目前这几种机型都存在或多或少的缺点，链夹式的栽植效率欠佳，吊篮式的栽植鸭嘴始终是垂直地面，摆线为余摆线，其垂直度较差，导苗管式移栽机的结构较为复杂[4-5]，综合考虑温室的情况不同于大田，面积较小，选择鸭嘴式连杆栽植器。栽植机构的设计会最终影响栽植效果[6]，目前有些移栽机的栽植直立度并没有达到很好的效果，在栽植频率较快的情况下，直立度较差，因此，针对这种情况提出了一种凸轮摆杆共同配合的栽植方式，结合鸭嘴式连杆栽植机构进行分析，通过对其结构以及参数进行优化，使栽植机构尽可能紧凑简洁，进而在工作过程中减少震动，提高稳定性，使之达到提高钵苗栽植效果的设计要求[7-8]。

1 结构及工作原理

1.1 整机结构及工作原理

手扶式半自动移栽机主要由发动机、车轮、链条、供苗机构、变速箱、鸭嘴开合控制机构、栽植机构、鸭嘴栽植器、覆土机构等结构组成，其整机结构简图如图1所示。

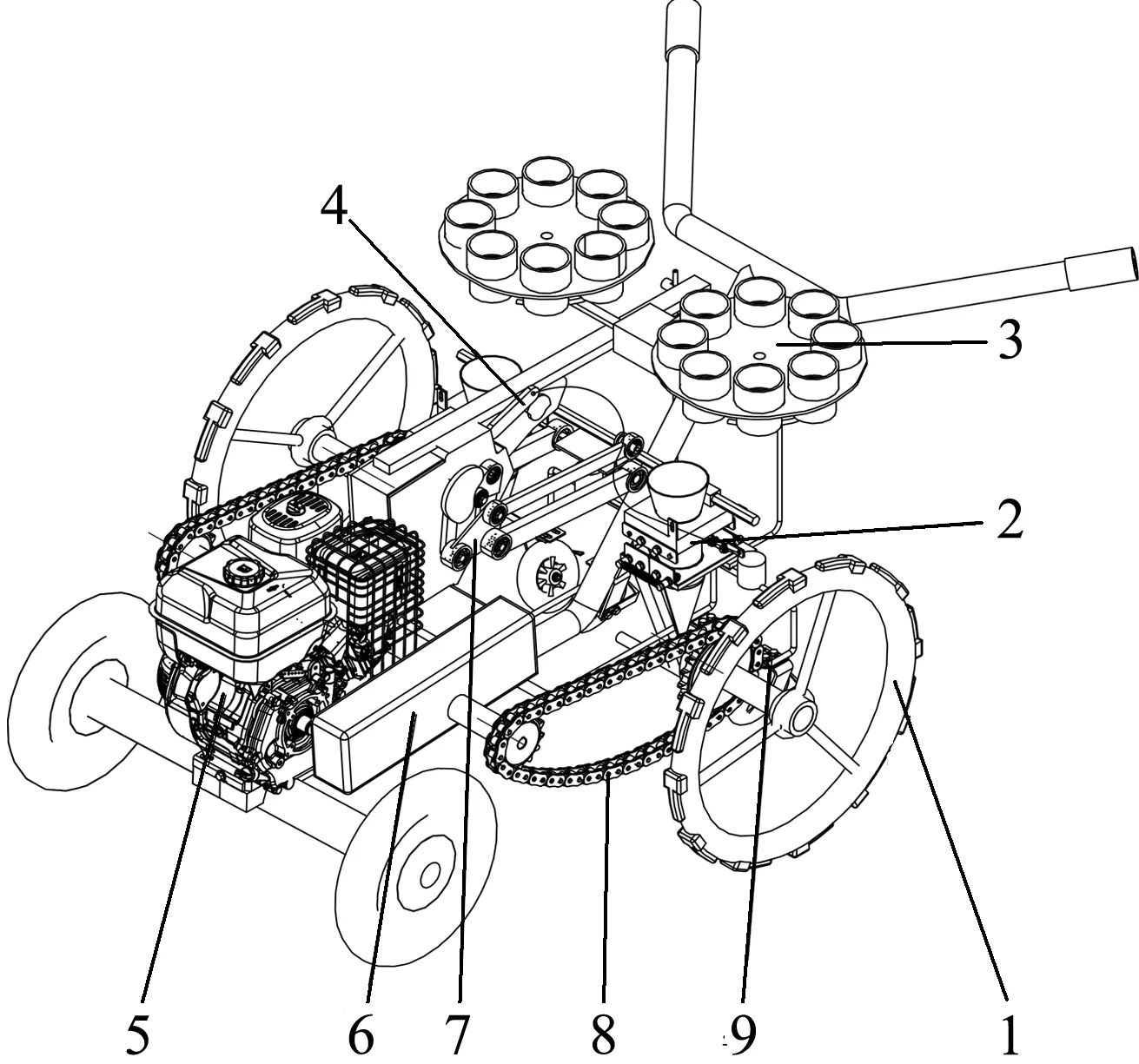
图1 整机结构简图

启动发动机，发动机将动力经过变速箱传输给栽植机构，实现预期的栽植轨迹运动，另外在鸭嘴栽植器入土一定深度时，鸭嘴需要张开进行放苗移栽工作，鸭嘴开合控制机构中的凸轮转动并带动拉线实现鸭嘴开合运动，当钵苗已经栽植入土后，鸭嘴离开钵苗，覆土机构进行镇压，保证钵苗有良好的直立度，完成一个周期的钵苗移栽动作。

1.2 栽植机构设计以及运动分析

栽植机构模型建立，如图2所示。图3为该移栽机的栽植机构简图，栽植机构的主动件分别为凸轮K以及曲柄BC，两者都以ω的角速度顺时针匀速转动，凸轮K将其中一个动力经过滚子R传递给摆杆MOA，使A点有一个运动，凸轮的作用主要是可以实现轨迹的平缓，在曲柄BC的带动下将另一个动力传递到D点，使栽植点有另一个的运动，因此，凸轮摆杆部分KMOA、曲柄连杆部分BCD共同影响栽植部分的运动。

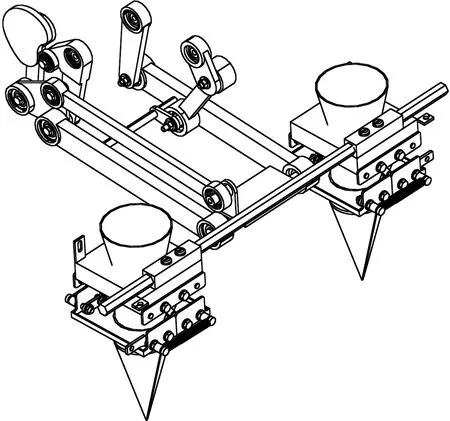
图2 栽植机构结构示意图

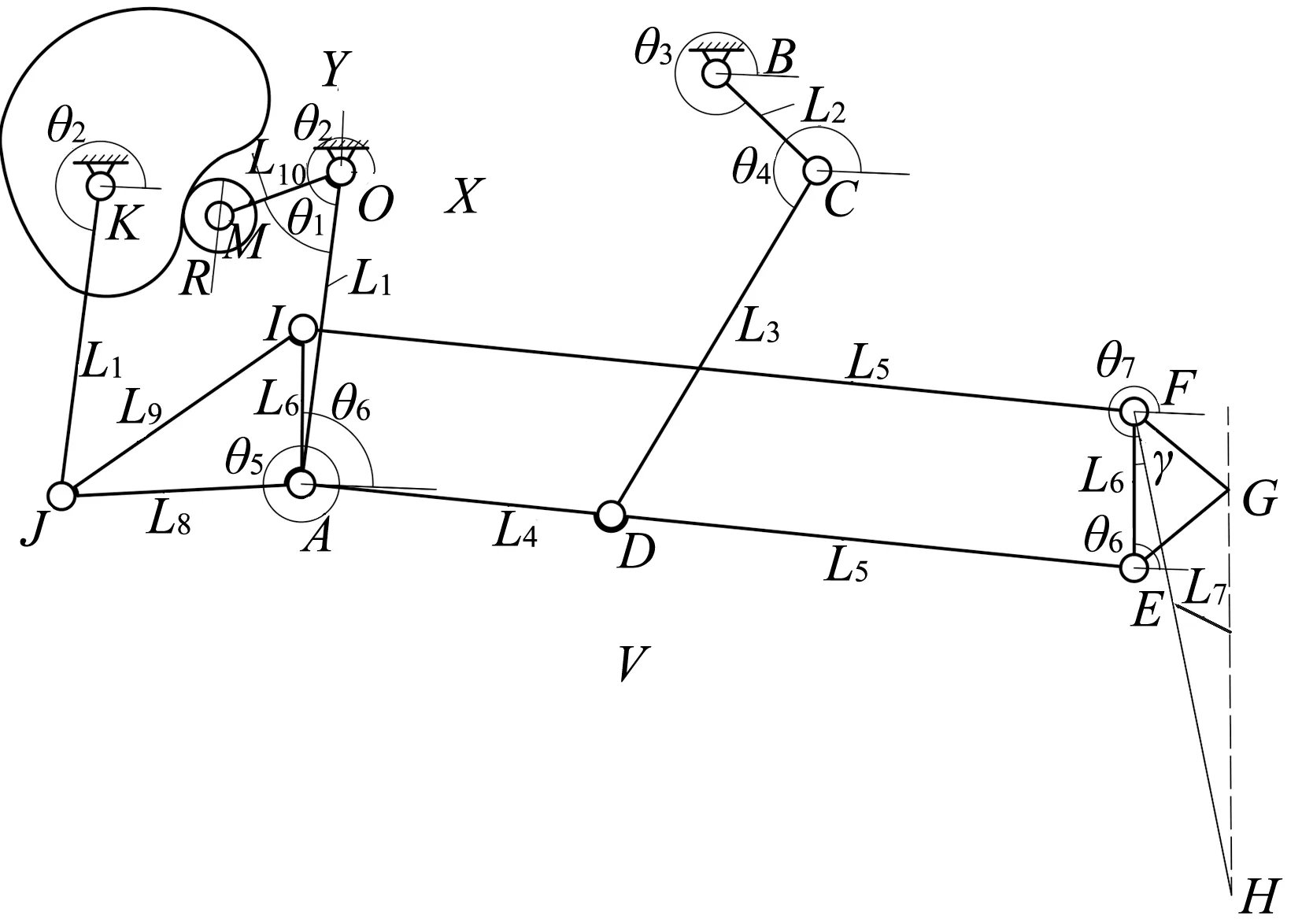
图3 栽植机构简图

栽植机构的运动轨迹可分为X方向以及Y方向，建立数学模型，表1为栽植机构数学模型参数表，和传统的栽植机构所采用的两个主动件都是曲柄的方案不同，该栽植机构的两个主动件分别是凸轮K以及曲柄BC，它们共同控制栽植点H的运动轨迹。由图3可知

F=3n-(2pl+ph)。

式中：pl——低副；

ph——高副。

表1 栽植机构数学模型参数表Tab. 1 Mathematical model parameter table of the planting mechanism

通过利用凸轮高副低代计算自由度，去除虚约束组件，其中n为8，pl为11，ph为0，所得自由度F为2，主动件为凸轮K以及曲柄BC，数量为2，具有确定的运动条件。

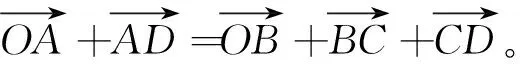
A点的轨迹分析，XO=YO=0。

(1)

C点的轨迹分析

(2)

D点的轨迹分析

(3)

对D点的轨迹公式进行整理简化分析可得(XA-XC)2+2(XA-XC)L4cosθ5+(YA-YC)2+2(YA-YC)L4sinθ5+L42-L32=0。

令a=2(XC-XA)L4；b=2(YC-YA)L4；c=L42-L32+(XC-XA)2+(YC-YA)2，则

E点的轨迹分析

(4)

F点的轨迹分析

(5)

H点轨迹分析

(6)

θ7=θ6+π+γ，考虑到会有移栽速度的影响，栽植轨迹会发生一定的变化

(7)

通过对式(7)求一阶导以及二阶导便得到了栽植点的速度与加速度方程。

2 MATLAB多目标函数求解

2.1 设计变量分析

通过对栽植点H轨迹进行分析，该栽植点与参数L1、L2、L3、L4、L5、L6、L7、θ2、θ3、θ7、φ1、φ2、XB、YB、V、t有关。考虑到移栽钵苗的尺寸、鸭嘴栽植器的尺寸设计以及安装尺寸，设置L7的尺寸为300 mm，另外L8、L9的尺寸为82、104 mm，凸轮K与曲柄BC以2π rad/s 的角速度顺时针匀速运动，凸轮将运动经过滚子与摆杆MO传递给摆杆OA，所以摆杆OA的摆角φ1是受凸轮控制的，φ1=f(ωt)，另外φ2=-ωt，φ1、φ2方向相反，凸轮K主要会对栽植轨迹的平稳性产生影响，对其他参数影响很小，可以忽略不计，所以事先选定一个凸轮形状以及位置，(XK,YK)为(-81.75，-6.39)，另外设滚子R直径、摆杆L10尺寸的初始值为32、48 mm，摆杆MO与摆杆OA之间夹角θ1为56°，取栽植机构各参数初始值对凸轮进行优化，对其轮廓不断进行调整，可以得到一条平缓的栽植轨迹曲线，最终得到一个较优的凸轮形状，如图4所示，由内而外的曲线分别为实际凸轮轮廓、滚子轨迹以及理论凸轮轮廓。

通过对栽植点进行分析，已知θ7是在一定范围内摆动，若已知γ，则可以推导出θ6。在栽植过程中V取500 mm/s，时间t为可控变量，B点要安装在减速箱上，参考现有机型对该点的位置进行提前设计选定，(XB,YB)为(139.08，35.72)，综上，栽植点的轨迹设计变量为X=[x(1),x(2),x(3),x(4),x(5),x(6),x(7),x(8),x(9)]=(L1,L2,L3,L4,L5,L6,θ2,θ3,γ)。

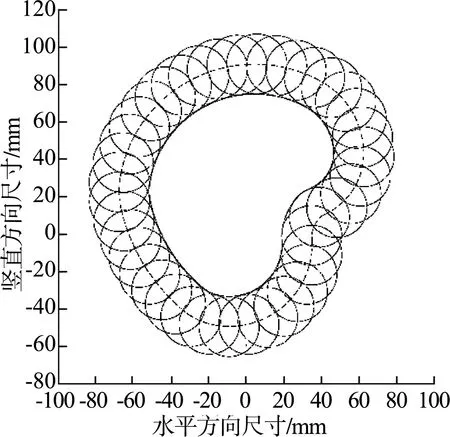
图4 凸轮轮廓曲线

2.2 目标函数栽植轨迹要求

移栽机的栽植轨迹对栽植效果有重要的影响，在移栽过程中直立度是衡量栽植效果的重要指标，一条合格的栽植轨迹的栽植高度必须大于钵苗的高度，才可以避免出现夹苗的现象发生。钵苗一般在30～45 d的期间内进行机械移栽，随着钵苗的根系不断生长发育，在进行移栽时的损伤率也会降低，考虑到栽植器的结构参数及工作参数的设计，选择40 d的72穴辣椒以及番茄钵苗进行移栽，钵苗的长度范围在130～170 mm 之间，茎秆2.2～3.1 mm之间，叶片在3～5片之间，叶面幅度不超过8 cm，如图5所示，尺寸合格的钵苗可以避免鸭嘴在开合过程中伤苗，减少钵苗在移栽过程中损伤率。

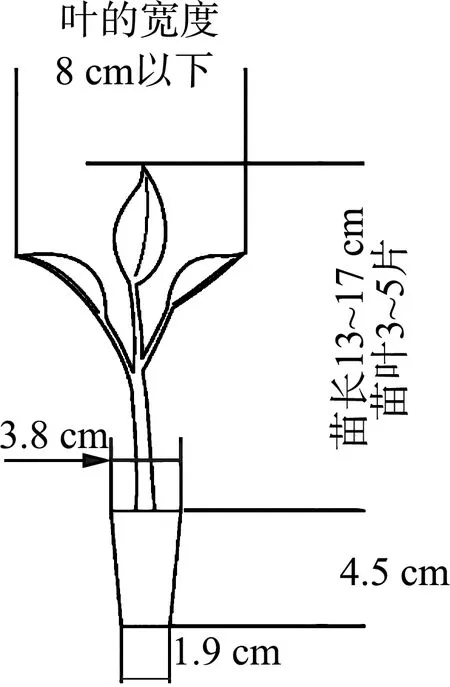
图5 钵苗示意图

综上，栽植轨迹的高度要比钵苗的高度高出一部分，栽植轨迹的高度定为250 mm；另外入土轨迹和出土轨迹尽量重合且与地面垂直，可以避免撕膜严重以及保证直立度；确保在栽植的过程中钵苗落入穴坑中的水平速度尽量为零，也就是所谓的‘零速栽植’，零速移栽在理论上可以保证在移栽过程中钵苗的直立度；栽植轨迹尽量平缓，凸轮的选择可以实现这一要求；在栽植的过程中，鸭嘴的摆角不宜过大，鸭嘴的摆角等效可以用θ7表示，其范围在285°～315°之间。当凸轮K与曲柄BC以2π rad/s的速度运转，机组以500 mm/s的速度前进，在一个周期内刚好形成一个完整的运动轨迹，在这个周期内进行轨迹分析。

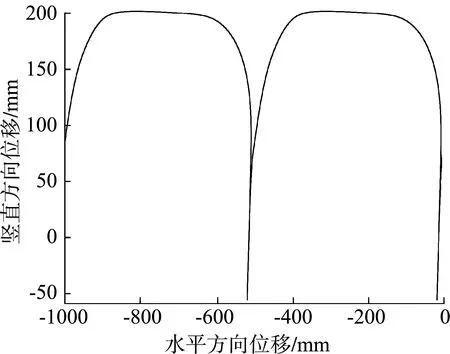
通过分析可得移栽机栽植机构多目标优化函数的数学方程，其轨迹曲线如图6所示。

1) 栽植点H的Y方向最高点至少比最低点高出250 mm。

2) 栽植点H轨迹最低点以上150 mm范围内X方向的距离小于15 mm。

3) 栽植点H轨迹最高点以下10 mm范围内，所对应的X最大值至少比最小值大200 mm。

4) 连杆FH与水平面夹角在285°～315°范围内运动。

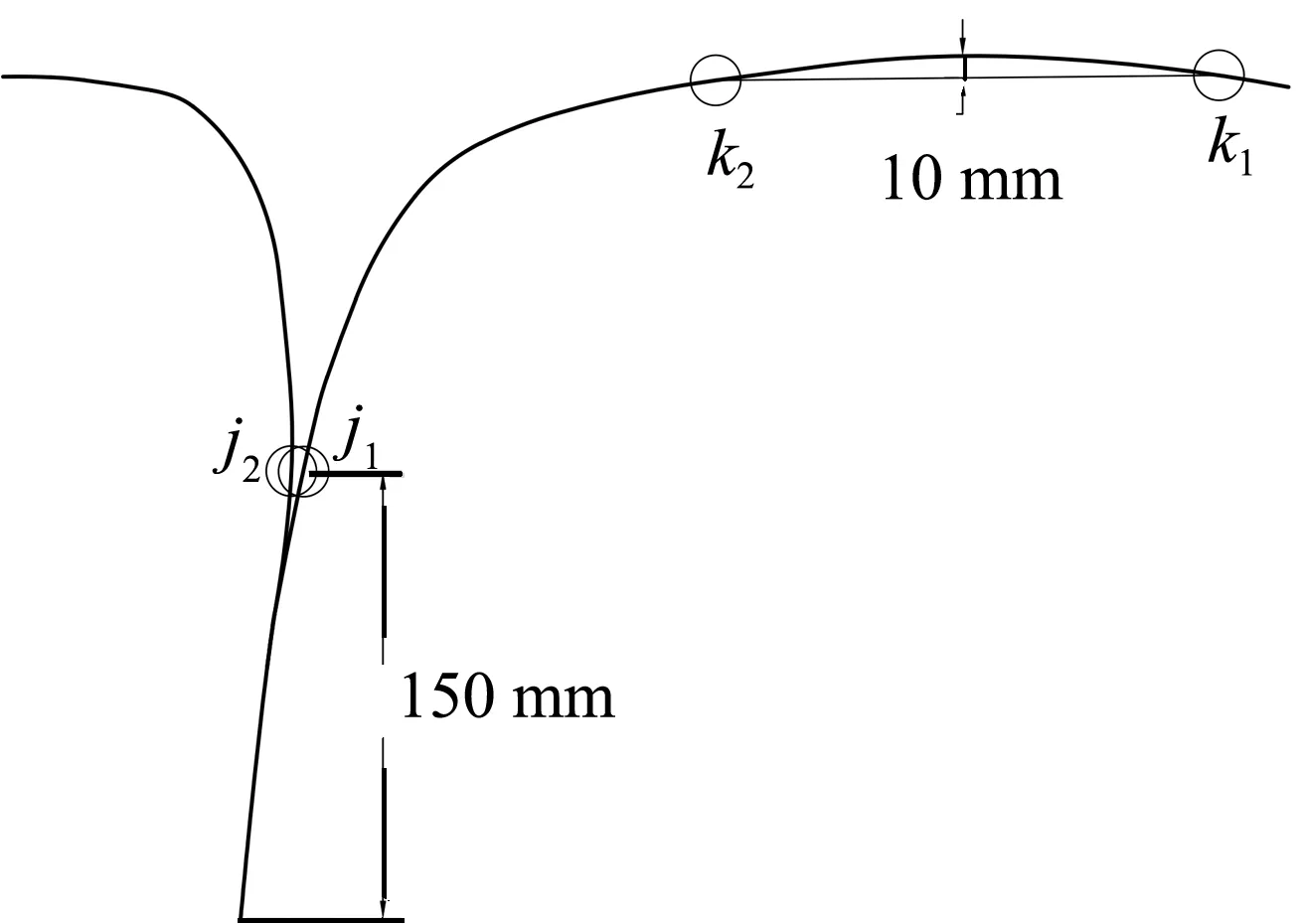
图6 目标轨迹示意图

转换为MATLAB语言可表示为

f(1)=min(YH(i))-max[YH(i)]+250

(8)

f(2)=max[XH(j1∶j2)]-min[XH(j1∶j2)]-15

(9)

f(3)=200-max[XH(k1∶k2)]+min[XH(k1∶k2)]

(10)

f(4)=max[θ7(i)]-315×∏/180

(11)

f(5)=285×∏/180-min[θ7(i)]

(12)

2.3 约束条件的确定

通过分析可知，移栽机栽植机构简图中存在五杆机构OBCDA，若想栽植机构运动平稳，则不能出现死点位置，则需要对△ACD进行分析

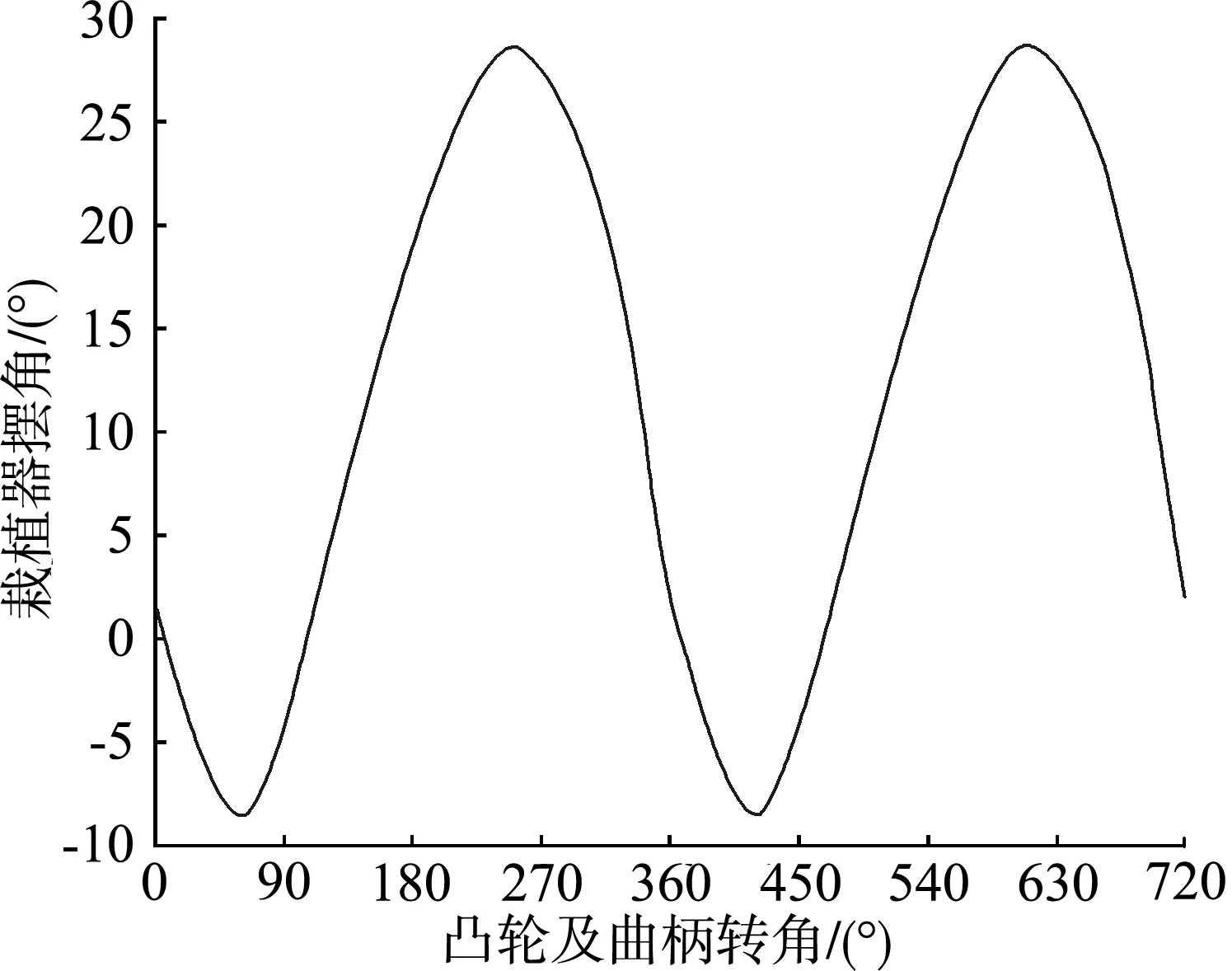
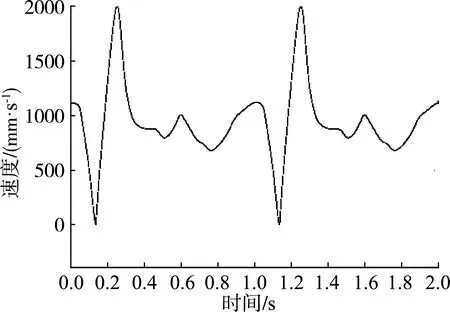
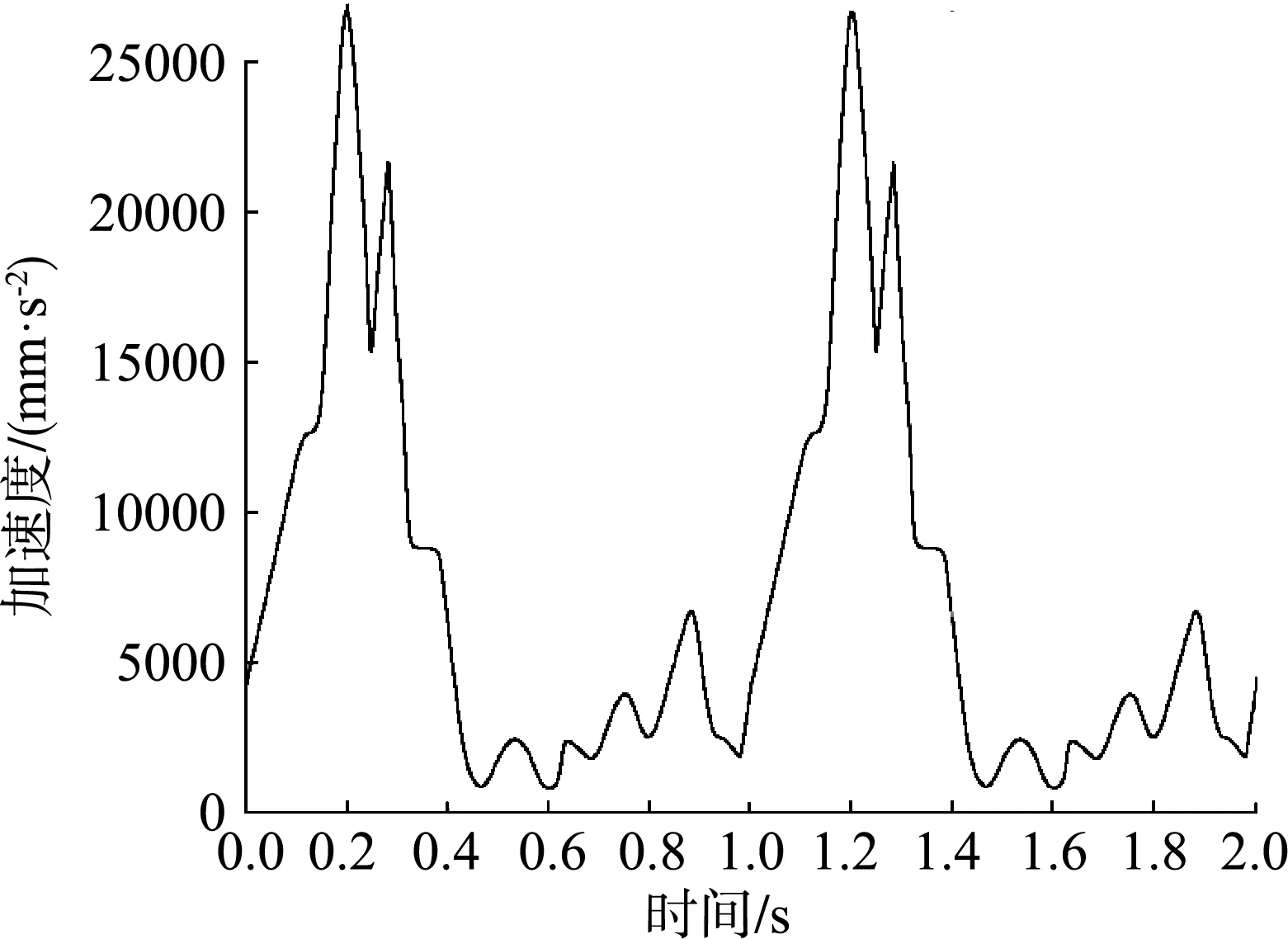
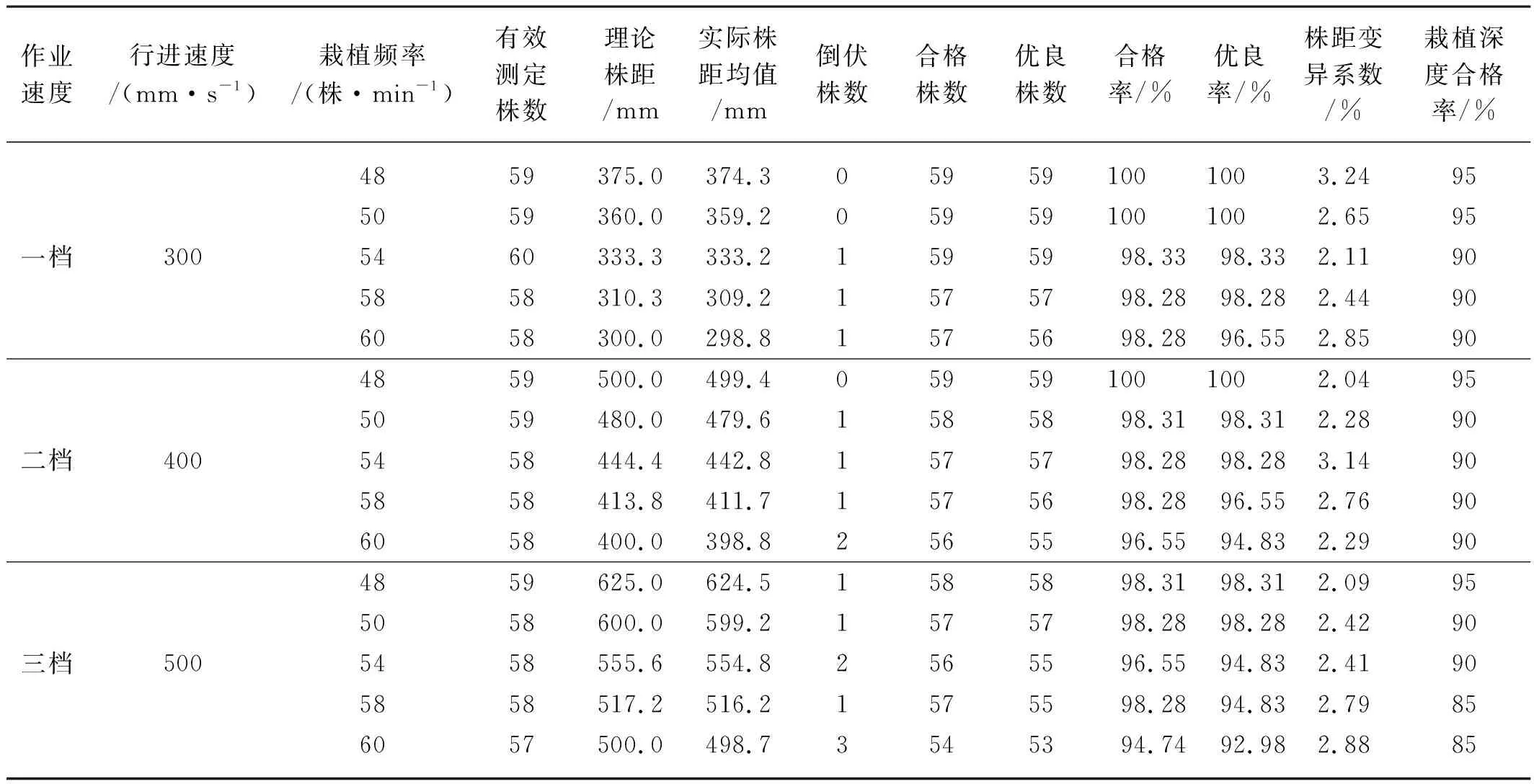
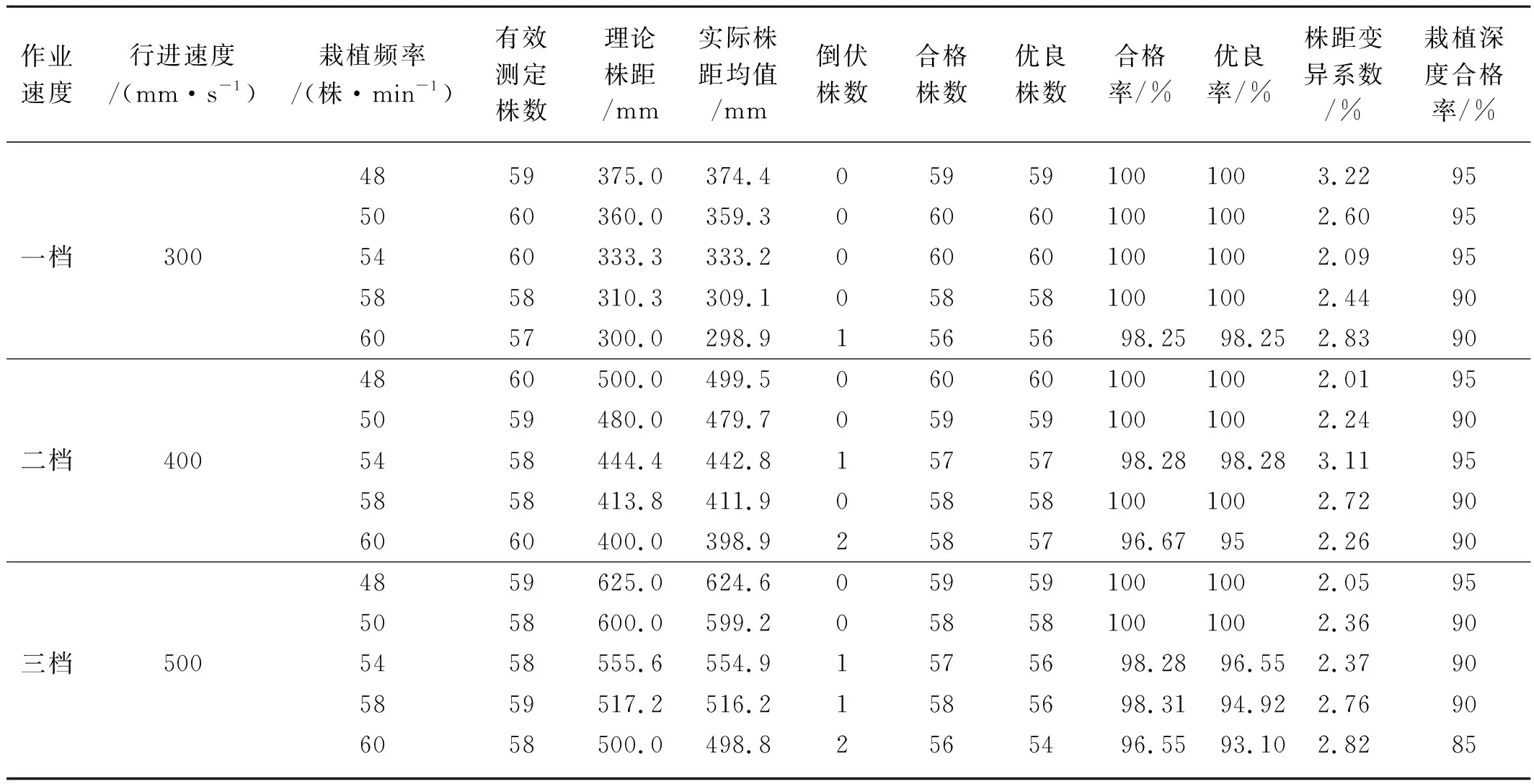
|L4-L3|

(13)

通过对上述对栽植点运动进行分析，将各点的位移代入上述公式可得栽植机构的约束函数

(14)

MATLAB软件具有强大的计算功能，可以使用优化工具箱中fgoalattain求解移栽机栽植机构复杂的多目标非线性规划问题，这种求解方式是把多目标转换为单目标，然后给每个目标函数一个权重weight，然后去求解，节省了大量的计算时间。以下是调用fgoalattain的格式:[x，fval，attainfactor，exitflag]=fgoalattain(‘fun’，x0，goal，weight，A，b，Aeq，beq，lb，ub，’nonlcon’)。

x为所求多目标函数的最优解；fval为多目标函数在最优解x处所对应的目标值；attainfactor是指目标到达情况，当attainfactor>=0时，fval没有溢出，attainfactor<0时，fval有溢出；exitflag为输出标记，当exitflag>0时，解收敛，相应的x、fval有效，反之为无效值。’fun’，’nonlcon’是所调用的目标函数以及约束函数的函数文件名称，x0是选定的一组设计变量的初始值，在这里设定x0的取值范围：x0=[120；50；150；125；320；60；255π/180；315π/180；10π/180]。

goal表示目标函数fun要逼近的目标值，它是一个向量，其维度等于目标函数fun的个数，已知栽植机构的目标函数有五个，所以goal的维度为5，goal=[0；0；0；0；0],weight表示目标函数的权值向量，其维度等于目标函数的个数，weight=[0.2；0.2；0.2；0.2；0.2]；A、b为不等式约束系数及右端项，Aeq、beq为等式约束系数及右端项，通过分析，该模型中不存在A、b、Aeq、beq，所以皆为空矩阵。lb、ub是设计变量的下限与上限，lb=[90；30；120；100；280；40；240π/180；300π/180；-π/6]；ub=[150；70；180；150；350；80；270π/180；330π/180；π/3]。

MATLAB中fgoalattain的优化过程经过多次迭代计算使得多目标规划中目标函数向量逼近目标goal，把目标函数、约束函数以及主程序整理输入MATLAB中[9-16]，可以得到最优解X=[128；52；150；120；336；60；256π/180；316π/180；8π/180]。

2.4 结果分析

根据MATLAB优化工具箱分析优化以及设置的其他连杆长度可以得到一组最优参数组合，l1=128;l2=52;l3=150;l4=120;l5=336;l6=60；l7=300;l8=82;l9=104;l10=48;θ1=56°;θ2=256°；θ3=316°;γ=8°。通过对栽植机构数学模型分析，在机组前进速度为500 mm/s，栽植频率为60株/min的前提下，利用MATLAB的绘图功能对该组结构参数下的栽植点进行两个栽植周期的轨迹、摆角、速度、加速度分析。

鸭嘴的栽植轨迹如图7所示，栽植轨迹的高度可达250 mm，株距50 mm，栽植深度在55 mm左右，入土点与出土点之间的间距在0.5～0.9 mm之间，栽植的穴口小，极大的缓解撕膜这种现象的发生，栽植轨迹最低点以上150 mm范围内，入土轨迹与出土轨迹的横向宽度在15 mm范围内，轨迹的垂直度与重合度高，另外栽植轨迹的最高点以下10 mm的范围内，栽植轨迹横向宽度可达200 mm以上，确保了在接苗过程中的动作平稳性要求，该曲线完全满足所设定的目标函数。

图7 栽植点轨迹曲线

鸭嘴栽植器摆角如图8所示，当凸轮与曲柄转过102°～123°时，鸭嘴摆角在-2.4°～2.4°之间摆动，处于栽植阶段，当曲柄转过113°时，鸭嘴摆角为0°，鸭嘴栽植点处于最低点，确保在栽植过程中钵苗可以垂直落入穴孔中，并且此时鸭嘴栽植点的速度也为零，也就是零速栽植，大大提高了钵苗的直立度，当曲柄转过265°时，鸭嘴栽植点为最高点，此时鸭嘴摆角为27.2°，摆角过大，此时对于接苗尤为不利，当曲柄转角为0°～20°时处于接苗阶段，摆角在-2°～2°之间，运动平稳，当曲柄转过10°时，摆角为0°，此时为最佳接苗点，可以大大提高接苗成功率。

图8 鸭嘴栽植器摆角曲线

栽植点的速度曲线以及加速度曲线如图9、图10所示，在栽植过程中，凸轮摆杆机构带动鸭嘴做预期的栽植轨迹运动，当栽植点处于最低点时，栽植点的速度接近于零速栽植，较低的运动速度便于钵苗下落平稳，鸭嘴栽植点的运动惯性小，保证钵苗初期与地面具有较高的垂直度，此时栽植点的加速度较大，回程时间大大缩短，鸭嘴在最低点到最高点的行程中，加速度先增后减，逐渐接近于零，速度变化幅度不大，栽植轨迹较为平稳，便于鸭嘴进行接苗工作。

图9 栽植点速度曲线

图10 栽植点加速度曲线

3 试验方法与分析

3.1 试验地点

试验地点为新疆乌鲁木齐市沙依巴克区农业机械化研究所的温室内，试验对象为40 d左右的辣椒苗及番茄苗，种植方式为覆膜双行半自动机械化操作。

3.2 试验指标

移栽机前进速度分为3个档位，对不同速度下的单行移栽频率的栽植效果进行分析。主要从3个方面对栽植效果进行评定，分别是株距均匀性、栽植深度合格率以及直立度。每次试验的株数为60株，将对其中任取20株计算其株距变异系数及栽植深度合格率。

1) 株距变异系数。在不同的前进速度下进行移栽，栽植鸭嘴会受到来自土壤的不同阻力，导致移栽速度会比理论值低，以株距变异系数为指标可以评测移栽机的栽植精度。

(15)

式中：CVX——株距变异系数；

SX——株距标准差；

2) 栽植深度合格率。栽植深度为h，若实际的栽植深度在(h-1 cm，h+2 cm)的范围内，则为合格。

(16)

式中：SV——试验采集中栽植深度合格的株数；

S——试验采集中总株数；

V——栽植深度合格率。

3) 直立度。根据旱地栽植机械农艺要求，栽植钵苗的主径杆与垄面之间的夹角α来评测直立度的合格率，当α越接近90°，直立度也就越好，当α>45°处于合格，α>70°则为优良。

直立度合格率

(17)

直立度优良率

(18)

式中：N——试验采集中总株数；

N1——试验采集中直立度合格的株数；

N2——试验采集中直立度优良的株数。

3.3 试验结果

首先对样机的栽植数据进行统计分析，如表2所示。其次对优化后栽植机构试验数据进行统计分析，如表3所示。

表2 优化前试验结果Tab. 2 Test results before optimization

表3 优化后试验结果Tab. 3 Test results after optimization

通过对优化前后的试验数据进行分析比较，优化后三个档位下的栽植效果均有得到改善与提高，例如一档频率下的58株/min所对应的栽植合格率和优良率均提高1.72%，60株/min所对应的优良率提高1.7%；二档频率下的50株/min所对应的栽植合格率和优良率均提高1.69%，58株/min、60株/min所对应栽植合格率和优良率均有不同程度的提高；三档下的五个频率所对应的栽植合格率和优良率全部得到了提高，另外株距变异系数和栽植深度合格率也得到一定的改善。

4 结论

1) 设计了一套关于凸轮摆杆的移栽机栽植机构，建立了相应的数学模型，通过对其运动进行分析，确定了相应的设计变量、约束函数以及目标函数，利用MATLAB优化工具箱中fgoalattain求解移栽机栽植机构复杂的多目标非线性规划问题，得到了栽植机构各参数的较优组合[128；52；150；120；336；60；256π/180；316π/180；8π/180]。

2) 对移栽机优化前后不同档位下的栽植频率进行移栽试验，对其数据结果进行统计分析，通过分析比较试验数据可知优化后的栽植效果相比于优化之前得到了不同程度的提高。例如一档频率下的60株/min所对应的优良率提高1.7%，二档频率下的58株/min所对应的合格率提高1.72%，优良率提高3.45%，三档频率下的60株/min所对应的栽植合格率提高1.81%。另外栽植株距均匀性以及栽植深度合格率也得到了不同程度提高。