衬砌厚度不足对隧道结构承载力的影响
2022-10-27许崇帮杨香英周幸宇
张 军,许崇帮,徐 筱,杨香英,周幸宇
(1.渝黔铁路有限责任公司,重庆 400037;2.交通运输部公路科学研究院,北京 100088;3.中铁十一局集团第五工程有限公司,重庆 400037)
0 引言
隧道运营过程中,难以避免地会遇到各种不同程度的病害问题,如衬砌厚度不足、材料劣化,裂缝等,这些病害往往是相互作用、相互影响的,其耦合作用最终直接影响整个隧道结构的整体承载性能。由于隧道衬砌结构的承载性也可作为直接体现隧道安全性、耐久性的指标,因此对隧道衬砌结构承载性能评价方法的研究是必要的。一套完备的衬砌解耦股承载性能评价方法对隧道的后期运营至关重要。对衬砌结构极限承载能力研究的基础是确定评判结构达到极限状态的指标。当前研究者认为,当衬砌结构一个截面达到其极限状态时,整体结构并不会立即破坏,该结构仍然可继续承载。当隧道在承载过程中的屈服截面个数增多到使超静定结构转变为机动结构时,结构才会破坏,丧失稳定[1-3]。因此,隧道衬砌结构临界失稳状态具有分段性[4-5]、模糊性[6-7]的特点。在隧道衬砌结构承载性能研究手段方面,多数研究人员主要借助于数值计算方法[8-11]和物理试验测试方法[12-14]。其中,王勇[8]利用素混凝土截面的抗拉和抗压强度验算公式计算出隧道承载能力,认为该承载能力为隧道极限承载能力,并定义安全系数为极限承载力和实际计算荷载的比值;张玉军等[9-10]认为裂缝深度的影响较大,而宽度的影响可以忽略,并认为压剪状态下裂纹的应力强度因子为零,在此基础上定义了带裂缝衬砌结构截面安全系数,以此判断带裂缝结构的稳定性和安全性。综上所述,隧道衬砌结构承载力的受控影响因素较多,不仅涉及隧道断面大小与形状、衬砌结构参数和围岩情况,还涉及对隧道最大承载能力确定识别的判断指标。
本研究根据已有的文献研究成果,首先明确了适合于隧道衬砌结构最大承载能力评判指标的标准。在此基础上,对隧道衬砌结构厚度不足的位置和厚度不足程度对隧道衬砌承载力的影响进行了分析,以期建立可供隧道衬砌结构承载评判参考的量化关系。
1 隧道衬砌承载力极限状态评判指标
隧道工程是一种复杂的系统结构,隧道衬砌的承载能力受多种因素影响,其中对隧道衬砌结构承载力极限状态的识别和判断是计算分析隧道衬砌承载力首先需要考虑的问题。本研究利用已有的隧道衬砌承载力室内物理模型测试数据,对隧道衬砌结构承载力极限状态的评判指标进行分析,建立可供数值计算中隧道衬砌结构承载力最大值的确定标准。
1.1 试验案例选取
选取5篇研究文献数据作为隧道衬砌承载力极限状态评判指标研究的样本案例。5篇研究文献数据中的相关数据信息如下:
(1)案例1
王士民等[15]以广深港高速铁路专线狮子洋隧道为依托进行了相似模型试验。试验隧道衬砌形态为圆形,外径5.4 m,内径4.9 m,厚度50 cm,材料为C50钢筋混凝土,配筋率0.48%,围岩为Ⅴ级,加载模型为边长60 m正方形,衬砌埋深24.6 m。试验表明,该衬砌在加载至第13级荷载时,隧道拱顶竖向荷载为1 252.2 kPa时,结构开始失稳。
(2)案例2
伍超等[16]以重庆市沙坪坝区双碑隧道为依托进行了相似模型试验。试验隧道衬砌形态为曲墙式,厚度70 cm,材料为C30钢筋混凝土,主筋为HRB335,配筋率0.6%,围岩为Ⅳ级,加载模型为边长90 m正方形,衬砌埋深37.35 m。试验结果表明,该结构在受到竖向荷载1 113.7 kPa时出现失稳特征。
(3)案例3
梁庆国[17]以宝兰客运专线通渭至榆中段上庄隧道为依托进行了相似模型试验。试验隧道衬砌形态为直墙式,厚度70 cm,材料为C25钢筋混凝土,配筋率0.6%,围岩为Ⅴ级,加载模型为60 m×28 m矩形,衬砌埋深5 m。试验结果表明,衬砌所受竖向荷载为1 550 kPa时,结构出现破坏。
(4)案例4
刘学增等[18]以双车道80 km/h标准断面为原型进行模型试验。试验隧道衬砌形态为曲墙式,厚度50 cm,材料为C30钢筋混凝土,主筋为HRB335,配筋率0.6%,围岩为Ⅵ级,加载模型为60 m×40 m矩形,衬砌埋深10.37 m。共测试了1.58,50,100,160,200 MPa/m共5种弹性抗力,用以研究不同围岩级别下衬砌承载,试验测得衬砌在拱顶所受竖向荷载分别为162,1 000,1 387,1 602,1 695 kPa时隧道开始失稳。
(5)案例5
谭家麒[19]针对Ⅴ级围岩条件下的高速公路隧道进行了模型试验。试验隧道衬砌形态为曲墙式,厚度50 cm,材料为C30钢筋混凝土,主筋为HRB335,配筋率0.6%,围岩为Ⅴ级,加载模型为40 m×24 m矩形,衬砌埋深7 m,衬砌在拱顶所受竖向荷载为794.6 kPa时开始失稳。
以5个文献案例中9组隧道衬砌结构的极限承载力测试工况为计算分析工况,9组计算工程如表1所列,其中,工况1,2,3分别对应案例1,2,3,工况4~工况8数据为案例4的5种测试数据结果,工况9对应案例5的测试结果。

表1 工况与衬砌极限承载力对比Tab.1 Comparison of working conditions and ultimate bearing capacity of lining
1.2 衬砌破坏评判指标研究
鉴于工况4~工况8中分析对象为案例4的相同衬砌结构,其余工况为不同衬砌结构。为便于分析衬砌形态对各指标因素的影响,对工况4~工况8进行分析时,简称为“相同衬砌工况”,对工况1~工况3、工况9进行分析时,则简称为“不同衬砌工况”。
(1)衬砌轴力指标
隧道衬砌结构达到极限状态时,对应多种分析工况(衬砌极限承载力),隧道特征位置衬砌轴力分布如图1所示。

图1 极限状态时隧道特征位置衬砌轴力分布Fig.1 Distribution of lining axial forces at characteristic position of tunnel in limit state
由图1(a)可以看出,圆形衬砌与直墙式衬砌破坏时,各特征位置轴力均比曲墙式衬砌小,截面承受轴力的能力比曲墙式低,所受轴力因衬砌形式的变化而不同。由图1(b)可以看出,衬砌破坏时,各特征位置轴力随衬砌结构承载能力的增大而增大。
因此,隧道衬砌结构承载力达到极限状态时,隧道衬砌轴力与结构形式、尺寸、跨度及围岩情况等因素皆相关,故不宜作为衬砌破坏的评判指标。
(2)位移指标
隧道衬砌结构承载力达到极限状态时,隧道特征位置衬砌结构变形分布如图2所示。
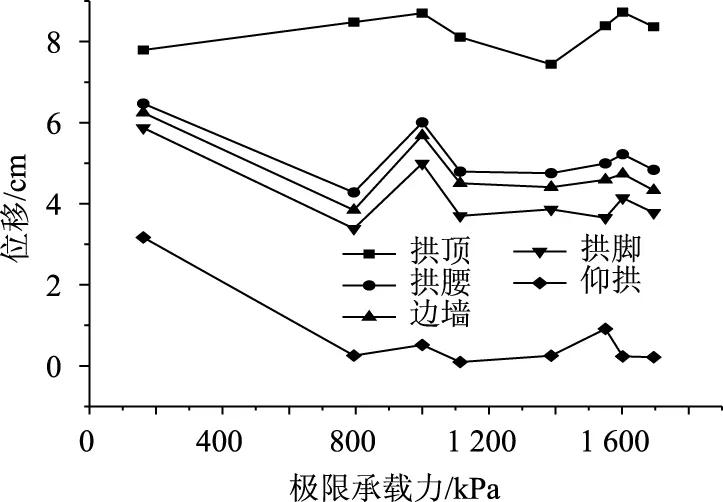
图2 极限状态时隧道特征位置衬砌变形分布Fig.2 Distribution of lining deformations at characteristic position of tunnel in limit state
由图2可以看出,隧道承载力达到极限状态时,隧道衬砌特征位置变形随衬砌承载能力变化的趋势大致相同,拱顶变形最大、仰拱变形最小,除仰拱中央处变形差距较大外,其他特征位置变形都相对稳定。其中,隧道拱顶处变形只有竖向变形,即拱顶沉降值,且最大变化率为14.73%,因此,各工况极限状态时衬砌拱顶沉降值相对稳定,规律较统一。
因此,可将衬砌拱顶沉降值作为评判隧道衬砌结构承载力极限状态的评判属性。
(3)衬砌结构破坏过程力学特性分析
以最大塑性应变值为评判指标,各计算工况随隧道衬砌结构所受荷载逐渐增大。隧道特征位置衬砌应力变化如图3所示。
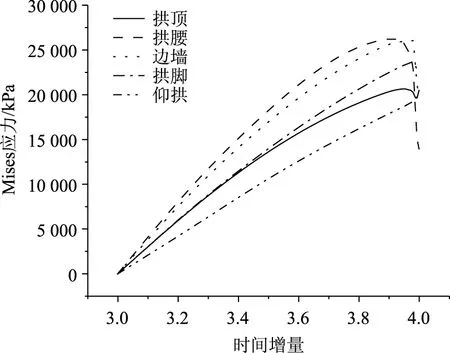
图3 加载过程隧道特征位置衬砌Mises应力变化曲线Fig.3 Mises stress variation curves of lining at characteristic position of tunnel during loading
由图3可知,隧道结构破坏过程中,隧道衬砌最大塑性应变值指标会出现突变,具有作为隧道衬砌结构承载力达到极限状态评判的可能。
为了讨论将最大塑性应变值作为评判指标的可行性,以工况9为例,分析隧道特征位置衬砌各指标突变点对应荷载,统计值如表2所示。

表2 加载过程隧道特征位置衬砌各指标突变点荷载统计(单位:kPa)Tab.2 Statistics of load on mutation point of lining indicator at characteristic position of tunnel during loading(unit: kPa)
工况9中隧道衬砌结构极限承载力为794.6 kPa,则表2中各指标突变点荷载误差如表3所示。

表3 衬砌各突变点荷载与工况9衬砌极限承载力误差Tab.3 Error between load on each mutation point of lining and ultimate bearing capacity of lining under working condition 9
从表3可以看出,隧道拱顶荷载与试验测得的荷载值最大误差仅1.48%,能够满足计算需要,因此将最大塑性应变值作为评判指标可行。
再以其他4组工况为例,隧道拱顶位置衬砌指标突变时对应的拱顶竖向荷载如表4所示。

表4 四种工况加载过程隧道特征位置衬砌指标突变点荷载(单位:kPa)Tab.4 Loads on mutation point of lining indictor at characteristic position of tunnel during loading under 4 working conditions (unit: kPa)
计算工况2衬砌破坏荷载为1 113.7 kPa,工况6破坏荷载为1 387 kPa,工况7破坏荷载为1 602 kPa,工况8破坏荷载为1 695 kPa,与上述突变点荷载作对比,误差如表5所示。

表5 四种工况加载过程衬砌指标突变点荷载与试验衬砌极限承载力误差(单位:%)Tab.5 Errors between load on each mutation point of lining indictor and ultimate bearing capacity of test lining during loading under 4 working conditions (unit: %)
从表5可以看出,隧道拱顶的计算荷载值与实际测试荷载值最大误差为8.26%(工况6),小于10%的误差,在工程计算中可以接受。因此,以最大塑性应变值作为评判指标能够满足对隧道承载力状态的研判要求。
综上分析,隧道衬砌结构承载力计算分析中,可采用隧道衬砌拱顶沉降值和最大塑性应变值作为隧道衬砌结构承载力极限状态值的评判指标。
2 隧道衬砌厚度不足对承载能力评价
2.1 评价方法构建
(1)隧道衬砌厚度不足的程度量化
设隧道衬砌结构设计厚度为S、衬砌结构环向长度为L,衬砌厚度不足部分的实际厚度为S′,厚度不足部分的环向长度为L′,隧道衬砌结构厚度不足程度用式(1)表达:
(1)
即隧道衬砌待评单元内厚度不足状态下的体积与延米内正常情况的体积之比α0∈[0,1]。对于完整隧道衬砌结构,α0∈1,隧道衬砌结构存在厚度不足越严重,α0值越小。
对于确定的衬砌结构,当α0为某一值时,存在多种不同S′和L′值组合,其中S′越小对隧道衬砌结构安全性越不利,对隧道衬砌结构承载能力的影响越严重。为反映这种差异性,引入厚度的敏感性指标(函数)δ来反映S′对承载力的影响,δ为不同程度厚度不足衬砌极限承载力与特定工况衬砌极限承载力之比。α为隧道衬砌厚度不足对承载力的影响指标。因此,对式(1)做如下改进,α为隧道衬砌厚度不足对承载力的影响指标:
(2)
(2)厚度不足的部位量化
因隧道衬砌为左右对称结构,仅选取隧道衬砌结构断面的右半部分(或左半部分)进行分析,隧道衬砌结构厚度不足出现的范围为-90°~90°,以路面或设计高程为水平基准面。
隧道衬砌厚度的部位对承载力的影响指标(函数)为β,该指标值由其衬砌厚度不足的位置确定,其值为厚度不足衬砌极限承载力与完整衬砌极限承载力之比。
(3)厚度不足时衬砌结构承载力综合评价
假定已知的隧道衬砌结构无损伤时初始状态的承载力为P,隧道衬砌结构出现厚度不足后的结构承载力P′表述为:
P′=F(P,α,β)。
(3)
2.2 隧道衬砌厚度不足位置的影响分析
为探究隧道厚度不足出现位置对隧道衬砌承载力的影响,可假定衬砌厚度不足程度为衬砌厚度缺失50%(即0.25 m),厚度不足环向长度为5.13 m,其他物理力学参数按表1中工况9选取。若不考虑厚度不足位置的差异性及厚度敏感指标δ,仅考虑衬砌体积的缺失引起的衬砌承载能力变化,按式(1)对衬砌极限承载力进行折减,可得厚度不足衬砌的极限承载力假定值为763.932 kPa。
按照上述工况对厚度不足位置因素进行模拟计算。按照拱顶下沉值与最大塑性应变值作为评判指标对应拱顶竖向荷载的较小值作为衬砌结构的极限承载力特征值。各工况衬砌变形和塑性应变分布如图4~图5所示。
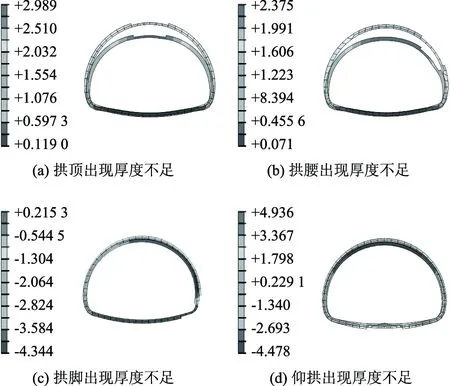
图4 极限状态下不同部位厚度不足时衬砌变形分布(单位:cm)Fig.4 Distribution of lining deformations in case of insufficient thickness at different parts in limit state (unit: cm)

图5 极限状态下不同部位厚度不足时衬砌塑性应变分布Fig.5 Distribution of plastic strains in case of insufficient thickness at different parts in limit state
由图4可以看出,当拱顶出现厚度不足时,衬砌变形趋势与工况9最接近,当其他部位出现厚度不足时,结构在围岩作用下整体向衬砌薄弱处挤压,导致衬砌薄弱处变形最大,越靠近衬砌薄弱处变形越大。
由图5 可以看出,削弱任意某个位置的衬砌,结构破坏时塑性应变最大点均出现在衬砌薄弱处。
根据衬砌破坏评判指标对衬砌不同位置出现厚度不足工况进行数值计算,得出衬砌结构极限承载力和厚度不足位置敏感性指标,如表6所示。
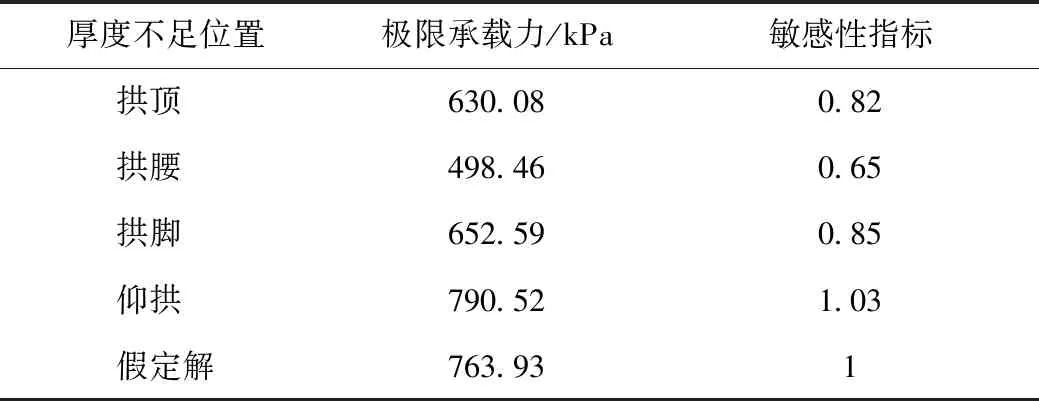
表6 不同位置厚度不足衬砌极限承载力及位置敏感性Tab.6 Ultimate bearing capacity and position sensitivity of lining with insufficient thickness at different positions
从表6可以看出,厚度不足出现在衬砌拱腰位置时对结构的承载能力产生了最大的负面影响,与衬砌承载力假定解偏差最大。厚度不足出现在仰拱处时,位置的影响因素几乎可以忽略不计,因此厚度不足位置对承载力的影响指标(函数)β的分布形式为分段函数,可表述为:

(4)
2.3 厚度不足程度的影响分析
因不同衬砌设计厚度不完全相同,不能仅以厚度不足处结构剩余厚度S′作为变量,为使敏感性指标δ更具有通用性,引入衬砌厚度剩余量ε,建立ε与δ的函数关系:
(5)
为得出厚度的敏感性指标δ,结合上述分析,控制厚度不足体积为每延米1.28 m3不变,选取5种厚度水平工况如下:
(1)S′=0.1,L′=3.21,ε=0.2。
(2)S′=0.2,L′=4.28,ε=0.4。
(3)S′=0.25,L′=5.13,ε=0.5。
(4)S′=0.3,L′=6.41,ε=0.6。
(5)S′=0.4,L′=12.83,ε=0.8。
为降低厚度不足部位对计算结果的影响,使厚度不足区域跨越尽量少的部位,假定厚度不足位置为拱顶,由上述分析可知,当厚度不足位置位于拱顶时,β值为0.82。综合考虑体积缺失与β值的修正,衬砌结构假定承载力应为626.42 kPa。各工况衬砌变形和塑性应变分布如图6~图7所示。
由图6可以看出,衬砌厚度不足引起的变形变化主要集中在厚度不足区域的边缘处,当衬砌病害处剩余厚度、环向长度均较小时,厚度不足边缘处受到挤压导致衬砌变形整体向病害处集中,当衬砌病害处剩余厚度、环向长度均较大时,厚度不足边缘处受到围岩挤压导致该处向衬砌净空侧下凹,病害区域中部相对来说反而呈现向围岩侧凸起的趋势。

图6 极限状态下不同程度厚度不足时衬砌变形分布(单位:cm)Fig.6 Distribution of lining deformations with different degrees of insufficient thickness in limit state (unit: cm)
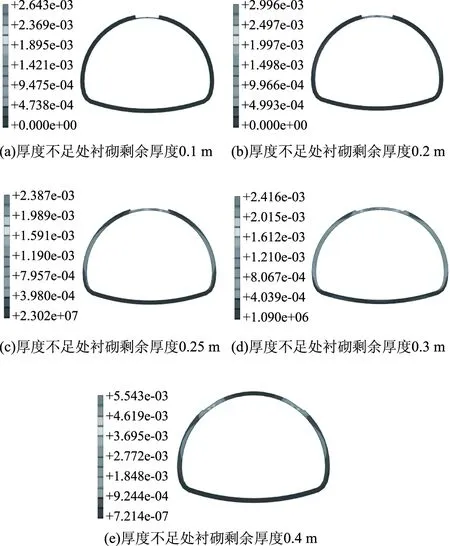
图7 极限状态下不同程度厚度不足时衬砌塑性应变分布Fig.7 Distribution of plastic strains with different degrees of insufficient thickness in limit state
由图7可以看出,衬砌应变在厚度不足处较大,且受厚度不足环向长度影响较大。当环向长度较小时,衬砌应变主要集中在厚度不足区域中部;当环向长度较大时,衬砌应变主要集中在厚度不足区域边缘处,该位置容易在围岩压力作用下下凹,产生较大应变。
根据衬砌破坏评判指标,对衬砌拱顶出现不同程度厚度不足工况进行数值计算,得出衬砌结构极限承载力和厚度不足程度敏感性指标,如表7所示。
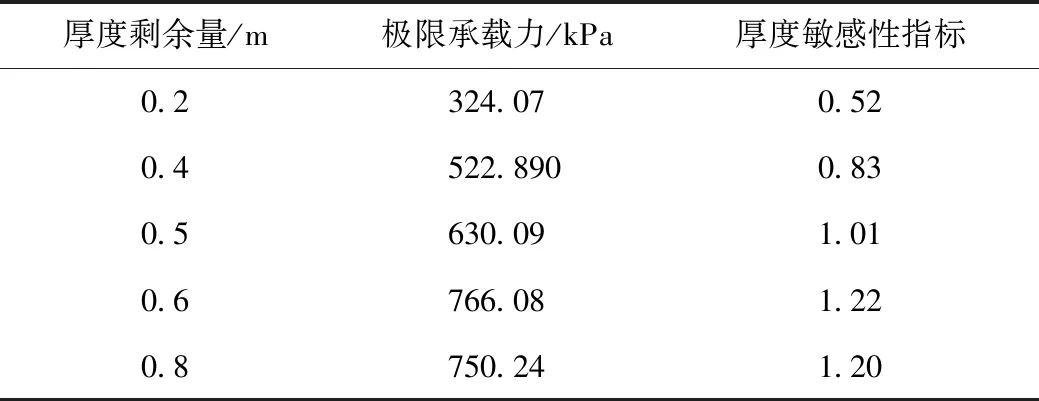
表7 不同程度厚度不足衬砌极限承载力及程度敏感性Tab.7 Ultimate bearing capacity and degree sensitivity of lining with insufficient thickness in different degrees
由表7可以看出,厚度剩余量为0.5时,衬砌极限承载力最接近假定值,厚度剩余量越小衬砌承载能力越差。建立厚度剩余量与其敏感性指标的函数关系,如图8所示。

图8 衬砌厚度剩余量与敏感性函数Fig.8 Residual lining thickness and sensitivity function
从图8可以看出,当厚度剩余量为0.8时,衬砌承载力比剩余量为0.6时略有降低,原因是厚度剩余量为0.8时厚度不足环向长度最大,且厚度不足区域自身承载能力已经较强,此时厚度不足,环向长度影响开始凸显,但该因素对结果产生的误差较小,可用函数关系近似表述为:
δ=-1.72ε2+2.91ε。
(6)
根据式(4)及(5),山岭隧道衬砌结构出现厚度不足后的结构承载力可以综合表述为:
(7)
式中,β与δ按式(4)与(6)确定。
3 结论
(1)将数值计算结果的衬砌薄弱位置的最大塑性应变量与该情况下的拱顶位移作比较,可以发现衬砌的最大塑性应变与拱顶最大位移正相关,故在实际判断中,可将隧道衬砌结构破坏计算值中采用拱顶下沉值与最大塑性应变值突变,作为隧道衬砌结构承载力极限状态的评判指标。
(2)当衬砌厚度不足位置出现在拱腰时,拱顶出现最大位移且该位置薄弱处的塑性应变最大,表明衬砌厚度不足出现在拱腰对结构承载能力影响最大。根据计算的不同衬砌厚度,可以发现衬砌厚度与结构承载能力负相关,即厚度不足程度越大,隧道结构承载能力所受负面影响越大。
(3)根据针对隧道衬砌的数值分析结果比值得到了厚度不足位置敏感性指标β。由数据计算点拟合出β的函数关系,结合衬砌不同厚度与不同位置的影响,建立了基于衬砌厚度衬砌结构承载能力评价公式。
