基于响应面法的斜拉桥动力模型修正方法
2022-10-27张立业王兵见吕竟铭
张立业,汪 波,王兵见,陈 可,吕竟铭
(1.交通运输部公路科学研究院,北京 100088;2.安徽省公路管理服务中心,安徽 合肥 230022)
0 引言
建立能够精确反映实际桥梁结构特性的基准有限元模型是进行结构分析、损伤识别和状态评估的关键[1-2]。由于实际桥梁结构的物理参数存在随机性和离散性,有限元模型采用的物理参数很难与实际桥梁结构一致,且建模过程中往往需要对边界条件和连续条件进行简化,致使桥梁结构有限元模型计算的特征参数与健康监测的特征参数存在一定的差异,进而影响桥梁结构分析、损伤识别和状态评估的准确率。获得能够精确反映实际桥梁结构的有限元基准模型需要借助健康监测数据和模型修正(Model Updating)技术。模型修正是通过优化结构有限元模型的几何物理等参数,使有限元计算的特征参数接近于结构健康监测的特征参数,其核心是最优化问题[3-4]。
常用的桥梁结构模型修正方法包括静力模型修正法[5-6]和动力模型修正法[7-8]。通过静力法测得的特征参数具有准确率高、抗干扰性强、适应性好等优点,但需要对桥梁结构进行荷载试验,获得静力响应数据,其加载方式单一,实测数据量有限,通常需要中断交通,因此,采用静力法进行桥梁结构模型修正是比较困难的。动力模型修正法以桥梁结构的模态参数作为特征参数,因模态参数反映了桥梁结构自身的特性,与加载方式无关,可通过环境激励的方法测得,无须中断交通[9],且大量研究表明:基于模态参数的损伤识别和状态评估方法对实际桥梁结构比较有效[10]。因此,动力模型修正方法更适用于实际桥梁结构,在桥梁结构健康监测中具有很好的应用前景[11-12]。
有限元模型修正的核心是最优化问题,构建合理的包含结构主要响应信息的目标函数是有限元模型修正的关键问题[13-14],目前已有不少学者基于实际桥梁结构或者室内试验模型的静动力测试数据[15-16],提出了比较有效的模型修正方法[8,17]。任伟新等[18]提出了一种基于响应面的模型修正方法;宗周红等[19-20]提出了一种基于响应面模型修正的桥梁结构识别方法,并应用于桥梁健康监测的有限元模型确认中;马印平等[21]提出了基于响应面法的钢管混凝土组合桁梁桥多尺度有限元模型修正方法;周林仁等[22]提出了基于径向基函数响应面方法的斜拉桥有限元模型修正方法;王晓光等[23]将稳健估计法引入响应面优化求解过程,提高了基于响应面模型修正的可靠性;Sanayei等[24]提出了一种基于多响应面数据的有限元模型修正和损伤识别方法。本研究在斜拉桥健康监测和参数化有限元分析技术的基础上,基于响应面法建立了斜拉桥动力模型修正方法,解决了斜拉桥有限元动力模型难于修正的问题,研究结果表明:修正后的有限元模型能够精确模拟实际斜拉桥结构,对斜拉桥的模型修正具有很好的适应性。
1 模型修正的基本原理
为了使有限元模型能够精确地反映实际桥梁结构的力学特性,除了建模过程中尽可能准确地选用符合实际的结构有限元模型参数,合理地处理边界条件和连续条件外,更重要的是要借助试验测试或桥梁监测结果修正有限元模型,这是获得高精度桥梁结构有限元模型的关键。
结构健康监测数据包括结构位移、应变、加速度等监测指标,特征参数指监测指标的极值、均值等时域特征,以及频率、振型等频域特征。由桥梁结构健康监测数据获得的1组特征参数为yi,m(i=1,2,3,…n),由桥梁结构有限元模型计算得到的1组与yi,m相对应的特征参数为yi,c(i=1,2,3,…n)。由于桥梁结构监测指标是实际桥梁结构的真实响应,其特征参数反映了结构的真实状态,因此,可以认为桥梁结构健康监测数据获得的特征参数yi,m是准确且可靠的。模型修正的主要任务是优化有限元模型参数xj(j=1,2,3,…,k),使yi,m和yi,c之间的误差最小。
桥梁结构有限元模型计算得到的yi,c可以看成是有限元模型参数xj的函数yi,c(xj),可以将yi,c(xj)和yi,m之间的误差函数作为有限元模型修正优化问题的目标函数。构造目标函数的途径有最小二乘法、Bayesian概率方法等,其中广泛应用的是最小二乘法。
(1)
式中,γi为各特征参数的权重,反映了各特征参数对有限元模型的影响程度,通常可以通过重要度或灵敏度方法来确定。
2 动力模型修正方法
振动频率、振型等模态参数是桥梁结构的固有特性,反映了桥梁结构几何尺寸、质量和刚度等主要几何物理量的分布特征。这些模态参数与加载工况无关,避免了监测过程中荷载工况差异所带来的误差。动力模型修正方法的一般过程包括:(1)建立待修正桥梁结构的初始有限元模型(FEM);(2)通过重要度或灵敏度等分析方法确定各几何物理参数权重并选取待修正参数xj;(3)根据待修正参数的重要度或者灵敏度确定待修正参数的变化倍率;(4)进行FEM计算,得到与实测结果对应的特征参数;(5)采用最小二乘法等回归算法分析FEM的计算结果,得出响应面方程;(6)建立形如式(1)的目标函数,确定各特征参数的权重系数;(7)采用最优化算法得出目标函数最优解,确定待修正参数的修正值。有限元模型修正的具体流程如图1所示。

图1 有限元模型修正流程Fig.1 Flowchart of finite element modification
由于桥梁结构动力响应与待修正参数通常存在着难以表达的隐性函数关系,响应面法可以通过建立响应面方程近似模拟这种隐性函数关系,其中,多元二次响应面方程是常用的响应面方程形式:
Y=AX,
(2)
其中
Y=[Y1Y2…Yi]T,
(3)
X=[1x1x2…xjx1x2x1x3…x1xj…
(4)
(5)
式中,A为响应面特征点参数;Y为桥梁结构特征参数向量;X为待修改正参数向量;Yi为桥梁结构特征参数;xj为待修正参数;aik为待定系数;i,j,k分别为桥梁结构特征参数、待修正参数和多元二次响应面方程待定系数的个数。
上述响应面方程反映了桥梁结构特征参数与待修正参数的函数关系,待定系数需要通过最优化方法得到,从而得出响应面方程。结合实际桥梁结构监测的特征参数,便能够建立起模型修正的目标函数。
3 基于频率监测的斜拉桥模型修正
频率是斜拉桥监测的重要指标,测试成本低且精度高,因此,基于频率监测指标来修正斜拉桥有限元模型的可行性较高。这里选用东海大桥主航道斜拉桥作为研究对象,其主跨为420 m,采用双向六车道加紧急停车带的高速公路标准。桥宽31.5 m,设计时速80 km/h。
3.1 修正参数的选取及其变化倍率
斜拉桥的主梁、桥塔和斜拉索的参数都会影响到斜拉桥的振动频率,因此选用主梁钢材密度、主梁钢材弹性模量、主梁混凝土密度、主梁混凝土弹性模量、主塔弹性模量和斜拉索弹性模量6个待修正参数。相对而言,斜拉桥频率对主梁钢材的参数更为敏感,故主梁钢材密度和弹性模量的变化倍率为1±0.2,其余参数的变化倍率为1±0.3,具体如表1所示。

表1 待修正参数及其变化倍率Tab.1 Parameters to be corrected and their change rates
3.2 试工况及有限元分析
采用参数化有限元分析技术,建立全桥初始有限元模型,选用Beam4单元模拟主梁混凝土,通过模态分析,得出各阶振动频率计算结果,由于低阶振动频率能够较好地反映桥梁结构状态,其中竖向振动频率影响最大,横向和扭转振动频率影响次之,且现实工程中很少发生。因此,选用前5阶振动频率进行修正,包括前3阶竖向振动频率,一阶横向和一阶扭转振动频率。恰当地选择频率修正阶数,可使模型修正精度既满足工程需要,又节约计算资源。实测和修正前频率如表2所示。

表2 实测频率与修正前频率Tab.2 Measured frequency and frequency before modification
有限元分析的振动频率和振型如图2所示。
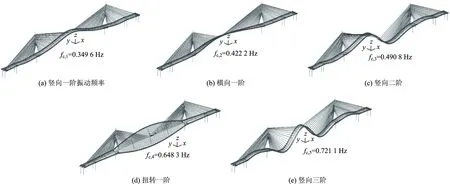
图2 模态分析振型图Fig.2 Mode shapes for model analysis
为了建立响应面方程,采用中心复合设计法来设计响应面的试验工况,由于待修正参数为6个,所以因子数为6,立方点数为64,轴向点数为12,α值为2.828。各代表性试验工况的有限元分析结果如表3所示,其中工况1~64为立方点,工况65~76为轴向点,工况77~82为中心点。

表3 代表性试验工况的有限元分析结果Tab.3 Finite element analysis result of representative test cases

由表3可以看出,各阶频率随着修正参数的倍率变化而变化,变化倍率越大、变化参数越多,对各阶频率影响越大,计算结果用于构建响应面方程,包括立方点(工况1~64)、轴向点(工况65~76)和中心点(工况77~82)。
3.3 响应面方程及目标函数
(6)
利用响应面方程的计算值与桥梁结构的实测值,建立的目标函数如下:
(7)
式中γi为各特征参数的权重值。
3.4 动力响应权重系数的确定方法
由式(7)可以看出,权重系数γi是影响目标函数优化结果的重要因素。本研究采用固定变量法分析各权重系数对目标函数的影响规律,用以选择最佳的动力响应权重系数,进而得出模型修正的最优化结果。
敏感性理论分析可知,式(7)中各动力响应权重系数对目标函数值的敏感性是不尽相同的,对于不同的工程应用情况,由于动力特征不同,其最优的权重系数也会有所不同,一个比较可行的方法是采用数值模拟的方法,具体工程具体分析。
拟定权重系数区间为0~1,采用固定变量法逐个分析γ1,γ2,γ3,γ4,γ5与振动频率变化率的相关系数,分析结果如表4所示。
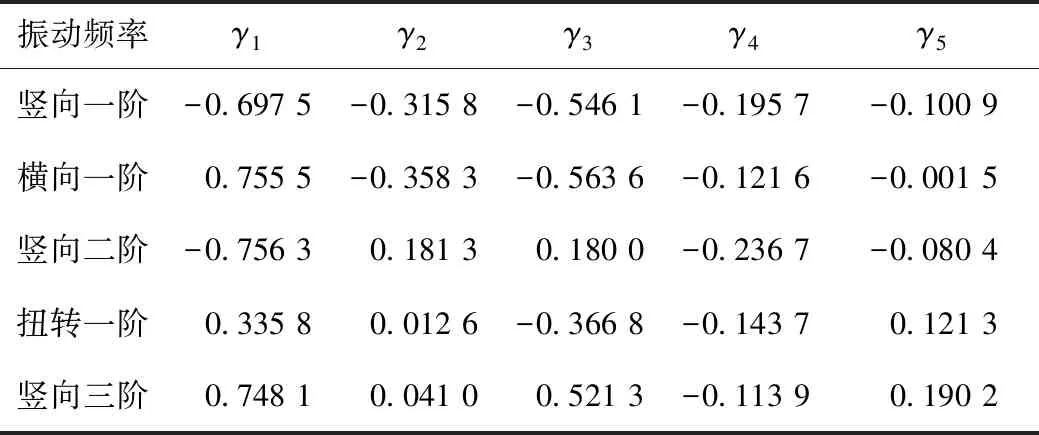
表4 权重系数与振动频率变化率的相关系数Tab.4 Correlation coefficient between weight coefficient and vibration frequency change rate
由表4可知,权重系数与各阶振动频率的相关性存在较大差异。对于该桥梁,权重系数γ1,γ2,γ3,γ4和γ5分别与竖向二阶、横向一阶、横向一阶、竖向二阶和竖向三阶的相关性较高,其相关系数分别为:-0.756 3,-0.358 3,-0.563 6,-0.236 7和0.190 2。选用相关系数的最大值作为权重系数可以得到均衡的全局最优化结果,对于有特殊要求的情况,可以选择关心阶次频率的相关系数最大值,以此保证在关心阶次频率上得出最优化的结果。
3.5 模型修正结果对比
由前面模态分析可知,前5阶模态中包含了竖向、横向和扭转振动频率。根据前面分析结果,这里选用相关系数的最大值[-0.756 3 -0.358 3 -0.563 6 -0.236 7 0.190 2]作为权重系数,得到均衡的全局最优化结果。
采用最优化方法求解目标函数,得到的优化结果为x1=0.923,x2=0.922,x3=0.773,x4=0.927,x5=1.384,x6=0.949。修正前与修正后的频率对比结果如表5所示。可知经过模型修正,有限元模型计算的振动频率值更接近于实际桥梁结构监测的振动频率值。
由图3可知,通过模型修正,有限元模型计算的振动频率值与实际监测的振动频率值的误差绝对值由2.03%~7.95%变化到0.05%~1.27%,其中一阶振动频率由-4.59%变化到-0.05%,几乎与实际监测的振动频率值一致。

表5 模型修正前与修正后的频率对比Tab.5 Comparison of frequencies before and after model modification

图3 模型修正结果Fig.3 Model modification result
4 结论
本研究建立了基于响应面法的斜拉桥动力模型修正方法,实现了斜拉桥有限元模型修正和健康监测数据快速分析。解决了响应面方程建立、目标函数求解和最优化算法等斜拉桥动力模型修正的关键问题,得出了斜拉桥动力模型修正的一般流程。实际桥梁结构算例表明:修正后有限元模型计算的振动频率值与实际桥梁结构监测的振动频率值的误差由2.03%~7.95%变化到0.05%~1.27%,其中一阶振动频率由-4.59%变化到-0.05%,几乎与实际监测的振动频率值一致,修正后的有限元模型能够精确的模拟实际斜拉桥结构,表明该方法对斜拉桥结构的有限元模型修正具有很好的有效性。
