基于感知信息的混凝土桥梁耐久性智能诊断方法

2022-10-27李殿斌

公路交通科技 2022年8期

李殿斌，李伟，陈南

(1.中国公路工程咨询集团有限公司，北京 100089；2.交通运输部公路科学研究院，北京 100088)

0 引言

一般大气环境中,桥梁结构混凝土碳化现象是造成混凝土桥耐久性下降的重要原因，揭示结构混凝土碳化机制,实现对碳化深度的预测，对于提升混凝土桥耐久性的诊断水平具有重要意义。国内外学者对桥梁混凝土碳化开展了一些研究，Papadakis等[1]研究了混凝土水化反应的机理，推导了反映混凝土碳化过程的化学式，揭示了碳化过程中二氧化碳、氢氧化钙等物质浓度对碳化深度的影响机理。Ashraf[2]将实测感知信息用于不确定性分析，提出了表征碳化随机过程的不确定性预测模型。Pan等[3]采用三维和二维电镜观测手段，建立了水泥基胶凝材料的碳化过程的机制模型。Chen等[4]基于随机过程方法推导了用于预测混凝土碳化深度的算法模型。Valcuende等[5]采用二阶贝叶斯函数拟合出碳化深度经验公式模型，并采用实测数据对模型进行了验证。通常，桥梁结构混凝土碳化深度受环境温湿度的影响较大，也取决于混凝土自身工艺(如水灰比、掺合料含量等)因素，由于作用因素众多，各因素间又可以产生相互作用，现有预测模型通常无法全面分析混凝土碳化的内在复杂作用。近年来，随着人工智能技术的发展，学者们开始研究采用神经网络等不确定性方法进行碳化深度预测，同时桥梁健康监测所提供的大量长期实测数据也为神经网络模型的建模提供了支撑[6～9]。已有研究建立的各种神经网络模型通常不考虑碳化的时间依赖性，而混凝土碳化是一个时效性很强的随机过程。因此，本研究在揭示一般大气环境中桥梁混凝土碳化机制的基础上，提出了基于时间依赖性的碳化深度神经网络预测方法，即把碳化反应随时间的变化与其他影响因素统筹考虑，形成一种BP-AR融合算法，实现对碳化深度的预测和修正，以达到提升模型预测精度的目的。

1 大气环境中桥梁混凝土碳化机理

桥梁结构在服役过程中必然会出现不同程度的混凝土碳化，导致构件钢筋锈蚀及耐久性衰退。氢氧化钙是胶凝材料中导致水化反应的重要物质，当桥梁结构混凝土的孔隙中浸润的液体pH 值高于12.0时可以有效保护钢筋不被腐蚀[10～11]。但是，大气中的二氧化碳会通过混凝土孔隙的渗透作用逐渐向内部迁移，并与氢氧化钙等水化产物发生一系列复杂的反应，主要包括如下反应：

(1)CH+CO2→CaCO3+H2O；

(2)C1.7SH4+1.7CO2→1.7CaCO3+SiO2·4H2O；

(3)C3S+3CO2+αH2O→3CaCO3+SiO2·αH2O;

(4)C2S+2CO2+αH2O→2CaCO3+SiO2·αH2O。

其中，氢氧化钙和二氧化碳之间的中和反应会不断地降低孔隙渗透溶液的酸碱度，当酸碱度降到临界pH值以下时，混凝土保护层下的钢筋钝化层就会逐步失效，从而导致钢筋发生锈蚀现象。然后，FeO,Fe2O3和Fe(OH)3等锈蚀产物会造成混凝土开裂，从而使更多的侵蚀物质进入混凝土内，进一步降低混凝土结构的耐久性[12]。碳化主要受材料和环境因素的影响，并且具有明显的时效性特征。在材料因素方面，当混凝土水灰比下降，实际发生的碳化深度也会随之降低，而随着混凝土强度的增大，碳化深度反而会减小[13～15]。在环境因素方面，湿度对碳化深度影响较大，主要是因为其会影响碳化的速率，随着相对湿度增大，碳化速率会先增大再减小；有文献研究显示[16]，当大气中相对湿度在50%～70%之间时，混凝土的碳化速率达到峰值，此时引起钢筋锈蚀的风险也较高。此外，大量实测数据表明，碳化深度具有较强的时间依赖性，这是因为影响碳化深度的主要因素(温度、湿度、CO2浓度等)随着时间的推移对水泥水化产物的化学反应具有累积效应[17～18]。所以，有必要建立一个能够考虑环境、材料诸因素影响以及时间依赖性的碳化深度预测模型。

2 AR-BP神经网络模型

自回归模型(AR模型)是自回归平均移动时间序列模型ARMA(Auto Regression Moving Average)的一种典型表达式，其根据被预测对象的历史观测数据(含实时数据更新)，通过寻找数据外延的统计特性，构造特定的模型进行预测。普遍形式的ARMA模型可以表示为：

yt-φ1yt-1-φ2yt-2-…-φpyt-p=

εt-θ1εt-1-θ2εt-2-…-θqεt-q,

(1)

式中,φ为自回归系数；θ为移动平均系数；p为自回归阶数；q为移动平均阶数。

AR模型与现有经典BP神经网络相结合，形成BP-AR神经网络方法，其算法逻辑流程如图1所示。

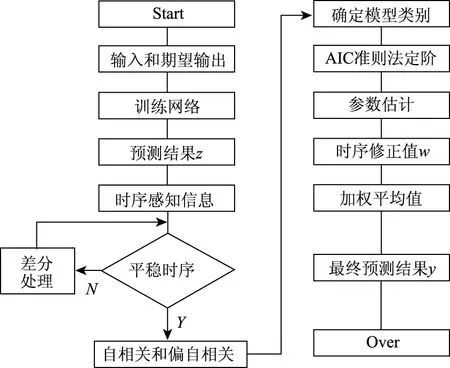
图1 BP-AR算法流程Fig.1 Flowchart of BP-AR algorithm

以上BP-AR算法流程用矩阵表示,如式(2)所示，其中xin是指被预测值(即碳化深度)相关的n个影响因素，在矩阵中一共有m组这样的影响因素集；ym为每行对应的预测结果的输出值，在本研究要建立的模型中ym代表碳化深度期望。

(2)

首先，确定BP神经网络中作为影响因素子集的n个输入值，设定作为预测结果的碳化深度值zi，并将其设定为BP神经网络的输出子集，输入输出的对应关系如式(3)所示。将综合模拟数据集分为训练集和测试集，此时还需要大量基于实测的数据(或试验数据)作为训练样本，实现对BP神经网络的训练，而测试集则用来验证所建立模型的正确性。

(3)

建立以温度、湿度、水泥用量、CO2浓度、水灰比、碳化时间6个影响因素作为输入层，建立3层结构的BP神经网络模型(模型层数增加虽然有利于训练结果，但是对计算量影响较大，本研究采用3层模型可以满足预测精度的要求)作为输出层。所建立的BP神经网络拓扑结构如图 2 所示，隐含层神经元节点数可由式(4)、式(5)来确定：

(4)

(5)

式中，m，n为输入层和输出层的神经元节点数；a为1～10之间的常数。

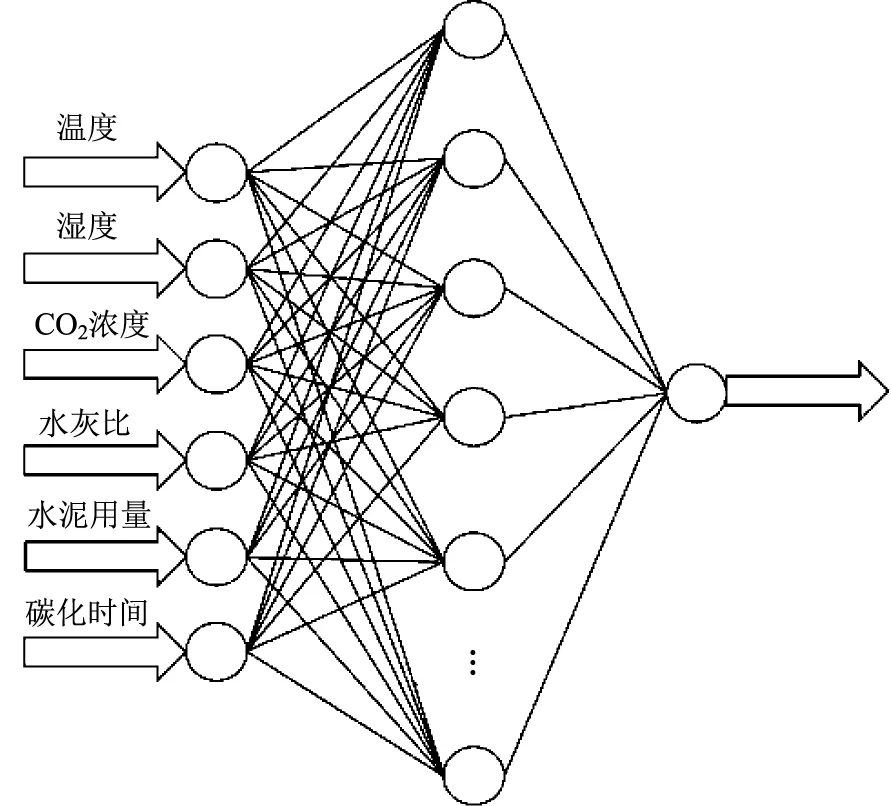
图2 BP神经网络拓扑结构Fig.2 Topological structure of BP neural network

然后，根据数据的时间顺序采用AR模型分析t-1至t-p时刻BP模型预测值随t变化而变化的规律，假设某个t时刻的碳化深度预测值为wt，并以此作为进一步修正得到的时序预测值：

Ptimeseries(zt-1,zt-2,…,zt-p)→wt。

(6)

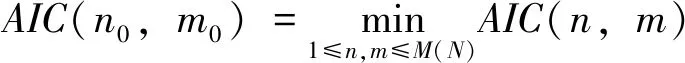
表1 ARMA模型定阶基本原则Tab.1 Basic principle of fixing order of ARMA model

在完成定阶后，需要开展模型参数的估计，本研究拟采用文献中经常出现的最小二乘估计方法来确定参数。最小二乘估计，通过计算时间序列数据信息的方差，得到实际值与估计值间的平方误差，当此误差期望值为最小时认定对应参数估计值为最佳。

yi=α1xi1+α2xi2+…+αnxin+ei(i=1,2,…，N)，

(7)

式中，y为感知信息数据；α为待估计参数；ei为零均值误差。

最后，与一般的BP神经网络不同，本研究还要在综合考虑各因素的基础上，进一步融合碳化速率时效性的影响，即将预测值zi与时序预测值wt按照式(8)进行加权平均统计，按照式(8)计算得出的结果即碳化深度预测值：

(8)

3 试验验证与分析

根据前面所建立的用于预测碳化深度的时间序列神经网络模型，本研究拟采用依托工程中采集的450余组感知数据(含试验数据)进行分析和验证。将工程中采集到的感知数据分别用作对BP神经网络进行训练的原始数据，以及开展测试需要的基本数据。采用分析软件对模型训练和回归过程进行演算，并且逐步调整计算过程，确定隐含层中神经元个数为13。BP神经网络的训练误差曲线与原始数据的拟合曲线如图3所示，由图中可见，当BP神经网络训练的目标误差为0.05时，此时的训练步数为2 919步并且达到最小误差要求，得到数据序列的拟合度R为0.827。

图3 BP神经网络的训练误差曲线与拟合曲线Fig.3 Training error curves and fitting curve of BP neural network

本研究设计了一种加速碳化的试验装置，制作两组不同工艺配方的混凝土测试件，每组测试件参数如表2所示。碳化深度的测量从第10 d开始至第110 d结束，测量间隔为每隔5 d测量一次。

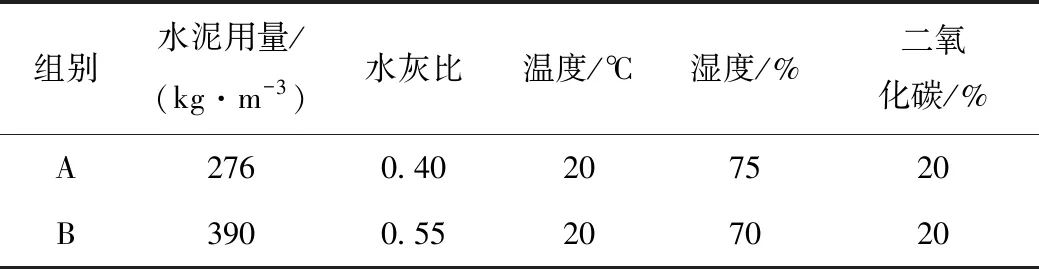
表2 混凝土试件相关参数Tab.2 Correlation parameters of concrete specimens

采用实测数据完成了对BP神经网络的训练，然后对两组时间序列数据开展碳化深度预测，分别标记为A组和B组，将各组中10～80 d的时间序列数据作为用于预测的数据，采用建立的BP-AR模型对80～110 d的碳化深度开展预测。采用自相关函数图和偏自相关函数法进行模型类型选择以及初步的模型定阶，使用 MATLAB 工具求得 A,B 两组数据的自相关(ACF)和偏自相关(PACF)函数图，根据自相关、偏自相关函数的计算结果可以判定，A组数据为较优数据组，更适合本研究建立的时序预测模型(图中显示，ACF拖尾，PACF截尾)，对A组数据确定模型阶数，相关的AIC准则函数计算如表3所示。

表3 A组数据AIC准则函数计算表Tab.3 Calculation sheet of AIC criterion function for data of group A

当n=3时，AIC值最小，故A组相对应的模型为AR(3)，即：yt=θ1yt-1+θ2yt-2+θ3yt-3(t=4,5,…,15)，采用LS法计算时间序列方差估计参数，计算得到A组的最终预测模型为：

yt=1.22yt-1-2.54yt-2+0.92yt-3。

(9)

同理，根据B组的AIC准则函数计算结果，选用AR模型对B组数据进行计算，确定模型阶数与A组数据一致，AIC准则函数计算如表4所示。

表4 B组数据AIC准则函数计算表Tab.4 Calculation sheet of AIC criterion function for data of group B

根据上述结果，B组数据模型的阶数为2，即当n取2时准则函数计算值最小，采用LS法计算时间序列方差估计参数，计算得到B组的最终预测模型为：

yt=1.33yt-1-0.915yt-2。

(10)

由式(9)、式(10)分别计算两组时间序列的预测值，预测时间范围为85～110 d，每间隔5 d得出一个预测值，总共得出6个碳化深度值，将BP-AR网络预测值进行加权平均处理，得到本模型最终预测值y，预测结果与实测值的比较如表5所示。

表5 预测值与实测值比较验证结果Tab.5 Comparison and verification result of predicted value and measured value

根据以上预测结果可知，利用考虑时效性的时序神经网络方法测算的预测值比单纯采用BP神经网络的预测值具有更高的预测精度。为了直观反映时间因素对碳化深度的影响，将预测值和实测值随时间变化规律进行比较，如图4所示。从图中可以看出，碳化反应的时效性在预测过程中呈支配地位，从数据外延的角度考察，用于预测的数据组充分决定了后续时间被预测值的走向趋势；对于一般的BP神经网络而言，当某一时刻预测值出现较大误差时，下一时刻的时序修正值也会出现较大波动(B2中最大波动为2%)，这可能是造成一般BP神经网络误差较大的原因。然而，在充分考虑时效性后，基于BP-AR模型的预测过程对之前碳化深度值的时变规律有充分的把握，这将有助于提升预测结果的精度和可靠性。因此，由于建立的模型是基于时间依赖性的碳化深度神经网络预测方法，即把碳化反应随时间的变化与其他影响因素统筹考虑，形成一种BP-AR融合算法，实现了对碳化深度的预测和修正，达到了提升模型预测精度的目的。