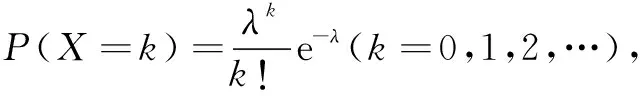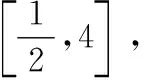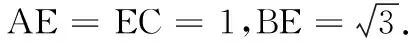高二数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1.设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x|x2-4x+3=0}，则U(A∪B)=( )

(A){1,3} (B){0,3}

(C){-2,1} (D){-2,0)

2.“logam>0”是“(a-1)(m-1)>0”的( )条件.

(A)充分非必要

(B)必要非充分

(C)充要

(D)既非充分也非必要

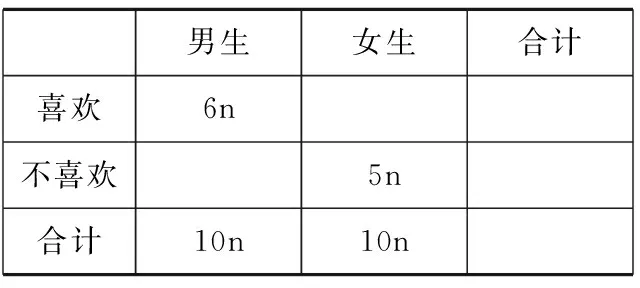
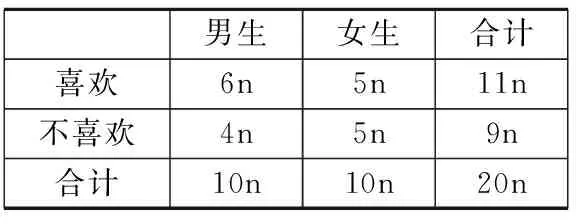
(A)b

(C)b

5.若(2x-1)4=a4x4+a3x3+a2x2+a1x+a0,则a0+a2+a4=( )

(A)40 (B)41 (C)-40 (D)-41

7.某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3,且p3>p2>p1>0.记该棋手连胜两盘的概率为p,则( )

(A)p与该棋手和甲、乙、丙的比赛次序无关

(B)该棋手在第二盘与丙甲比赛,p最大

(C)该棋手在第二盘与乙比赛,p最大

(D)该棋手在第二盘与甲比赛,p最大

(A)函数f(x)的定义域是[-4,2]

(B)函数y=f(x-1)是奇函数

(C)函数f(x)的图象关于直线x=-1对称

(D)函数f(x)在区间[-1,2)上是减函数

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

9.图中阴影部分用集合符号可以表示为( )

(A)B∩(A∪C)

(C)B∩U(A∪C)

(D)(A∩B)∪(B∩C)

11.有5位志愿者主动到3所山区学校参加支教活动,要求每所学校至少安排一位志愿者,每位志愿者只到一所学校支教,下列结论正确的有( )

(A)不同的安排方法数为150

(B)若甲学校至少安排两人,则有60种安排方法

三、填空题(本大题共4小题,每小题5分,计20分)

13.命题“∀x>1,x2-x>0”的否定是______.

14.从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为______.

15.已知函数f(x),g(x)的定义域均为R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7.若y=g(x)的图象关于直线x=2对称,g(2)=4,则f(1)=______.

16.已知x=x1和x=x2分别是函数f(x)=2ax-ex2(a>0且a≠1)的极小值点和极大值点.若x1

四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知幂函数f(x)=(m2-3m+3)xm的图象关于y轴对称,集合A={x|1-a

(1)求m的值;

18.(本小题满分12分)甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.

(1)求甲学校获得冠军的概率;

(2)用X表示乙学校的总得分,求X的分布列与期望.

(1)当m=3时,求f(6,y)的展开式中二项式系数最大的项;

20.(本小题满分12分)某学校对男女学生是否喜欢长跑进行了调查,调查男女生人数均为10n(n∈N*),统计得到以下2×2列联表,经过计算可得K2≈4.040.

男生女生合计 喜欢6n 不喜欢5n 合计10n10n

(1)完成表格求出n值,并判断有多大的把握认为该校学生对长跑的喜欢情况与性别有关;

(2)① 为弄清学生不喜欢长跑的原因,采用分层抽样的方法从调查的不喜欢长跑的学生中随机抽取9人,再从这9人中抽取3人进行面对面交流,求“至少抽到一名女生”的概率;

② 将频率视为概率,用样本估计总体,从该校全体学生中随机抽取10人,记其中喜欢长跑的人数为X,求X的数学期望.

附表:

P(K2≥k0)0.100.050.0250.0100.001 k02.7063.8415.0246.63510.828

21.(本小题满分12分)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.

(1)证明:平面BED⊥平面ACD;

(2)设AB=BD=2,∠ACB=60°,点F在BD上,当∆AFC的面积最小时,求CF与平面∆ABD所成的角的正弦值.

22.(本小题满分12分)已知函数

(1)求函数f(x)在[-3,3]的值域;

(2)设g(x)=f′(x)-xex+5x+1,已知x1+x2≥0,求证:g(x1)+g(x2)≥4.

参考答案

一、单项选择题

1.D;2.A;3.C;4.D;5.B;

6.D;7.B;8.C.

二、多项选择题

9.AD;10. BCD;11.AC;12. BC.

三、填空题

四、解答题

17.(1)由幂函数定义,知m2-3m+3=1,解得m=1或m=2.

当m=1时,f(x)=x的图象不关于y轴对称,舍去;当m=2时,f(x)=x2的图象关于y轴对称.因此m=2.

由题意知BA,故解得a≥1.

(2)依题可知，X的可能取值为0，10，20，30.

P(X=0)=0.5×0.4×0.8=0.16,P(X=10)=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44,P(x=20)=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34,P(X=30)=0.5×0.6×0.2=0.06.故X的分布列为

X0102030P0.160.440.340.06

E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.

20.(1)2×2列联表如下表所示:

男生女生合计 喜欢6n5n11n 不喜欢4n5n9n 合计10n10n20n

21.(1)因为AD=CD,E为AC的中点,所以AC⊥DE.

在∆ABD和∆CBD中,由AD=CD,∠ADB=∠CDB,DB=DB,得∆ABD≌∆CBD,有AB=CB.

又因为E为AC的中点,所以AC⊥BE.

又DE,BE⊂平面BED,DE∩BE=E,所以AC⊥平面BED.因为AC⊂平面ACD,所以平面BED⊥平面ACD.

因为∆ABD≌∆CBD,所以CB=AB=2.又因为∠ACB=60°,所以∆ABC是等边三角形.

显然φ′(x)在R上单调增且φ′(0)=0,故φ(x)在(-∞,0)单调减,在(0,+∞)单调增,可得φ(x)min=φ(0)=4>0,即g′(x)>0,于是g(x)在R上单调增.

令F(x)=g(x)+g(-x)=ex+e-x-x2+2,则F′(x)=ex-e-x-2x,令G(x)=ex-e-x-2x,则G′(x)=ex+e-x-2≥2-2=0,等号当且仅当x=0时成立,故函数G(x)在R上单调增.而G(0)=0,所以有F(x)在(-∞,0)单调减,在(0,+∞)单调增,可得F(x)min=F(0)=4.于是,∀x∈R, 有g(x)+g(-x)≥4.

由x1+x2≥0,得x1≥-x2.于是g(x1)≥g(-x2)等价于g(x1)+g(x2)≥g(x2)+g(-x2)≥4,即当x1+x2≥0时,g(x1)+g(x2)≥4成立.