一道联考题的多角度思考

王洪军

(内蒙古师范大学附属中学,010020)

(A) 2 (B) 3

(C) 4 (D) 以上都不对

视角1立足基础,踏实计算

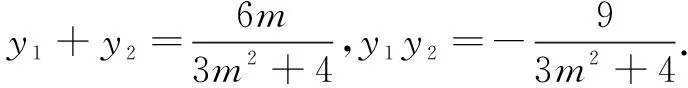
视角2利用二级结论

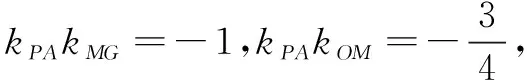
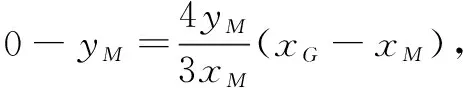
卡夫卡父子关系的痛苦之处在于：卡夫卡无法成为父亲，无法找到属于自己的坐标，更不可能用父亲的标准来衡量自己那个完全迥异的世界，而卡夫卡显然一生都受困于此；父亲的蛮横无理击溃了卡夫卡，以至于他认为一切困难都可以击倒他；而父亲粗暴的爱也并没有教会卡夫卡责任和承担，教会他勇敢地选择并为之付出代价。卡夫卡无法在内心树立起一个属于自己的强大形象，并达到最终真正的成长。

评注上述两种解答都是基于先确定点的坐标,进而得到所考虑线段的长度,其中解法2实施了“设而不求”这一常用策略,大大简化了运算量.

视角3数形结合

解析几何本来就是解决几何问题,只不过是借助坐标法来解决相应问题.其实,当题目中的几何关系易于把控时,不引入点的坐标而直接考察线段长度的关系也是可行的,这需要适当借助图形的几何关系开拓思维,更好地将各知识模块联系起来,在综合分析问题的基础上给出解决方案.

解法3如图2,设|PF1|=λ|F1A|(λ>0且λ≠1),|F1A|=m,则|PF1|=λm.设椭圆Γ的右焦点为F2,记θ=∠PF1F2.

在∆PF1F2中,由余弦定理,得|PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|cosθ,将条件代入,得(4-|PF1|)2=|PF1|2+4-4|PF1|cosθ,整理得

①

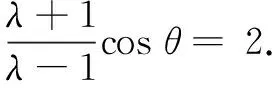
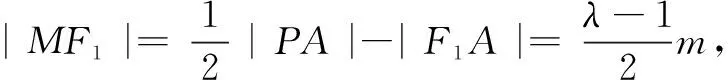
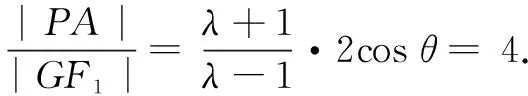
视角4利用圆锥曲线的统一性质

圆锥曲线中有很多统一的优美性质,能为我们的解题提供方便.注意到弦PA通过左焦点F1,这启发我们联想椭圆中类似的焦半径公式,进而得到如下解法.

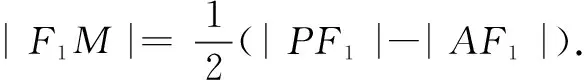
评注从上面的解答容易看到,我们已经得到了一个与椭圆离心率有关的拓展结论,具体表述如下:

上述结论在双曲线与抛物线中也有类似的表达,都可以借助上面的解法进行论证.至此,我们已经看到了问题中蕴含的普遍规律,也就是说它是基于上述结论命制的,是圆锥曲线统一性质的一个特例.