运用一题多变探究与(-1)n有关的数列求和问题*

迟丽杰 姜尚鹏

(山东省平度市第九中学,266700)

数列求和问题是高考试题中的常考题型,对于一些常用的数列求和方法,如公式法、分组求和法、错位相减法、裂项相消法、倒序相加法、并项求和法等,学生已经熟练掌握.但在平时教学中,笔者发现对与(-1)n有关的数列求和,学生常感到无从下手.根据平时教学中的一些积累,本文对与(-1)n有关的数列求和进行了梳理和总结,以变式探究的形式整理成文,与读者分享.

一、问题呈现

引例已知an=(-1)n(2n-1),求数列{an}的前n项和Sn.

解因为Sn=-1+3-5+7-9+11-…+(-1)n(2n-1),所以

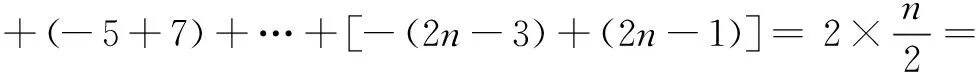
评注数列求和的关键在于分清数列通项公式的特点,由此选择相应的求和方法.此题是(-1)nf(n)型的求和问题(其中f(n)是等差数列的通项公式),因此根据等差数列相邻两项的差为定值的特点,采用分组求和法可简化问题;对n进行分类讨论求和时可用类比思想解题,也可以利用奇数项和与偶数项和的关系解题,如本题中当n是奇数时,n-1是偶数,则Sn=Sn-1+an=(n-1)-(2n-1)=-n.

二、变式探究

变式1若an=(-1)n2n,求数列{an}的前n项和Sn.

评注此题将引例中的f(n)换成了等比数列的通项公式,观察an=(-1)n2n,发现此题中的(-1)n与2n分别是两个等比数列的通项公式,其乘积的结果(-2)n也是一个等比数列的通项公式,由此转化,可以直接用等比数列的前n项和公式求和.

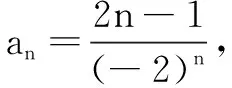
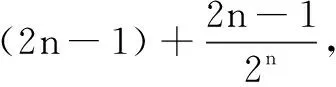
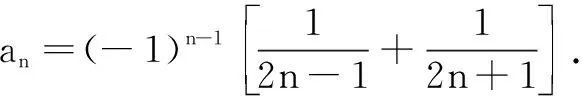
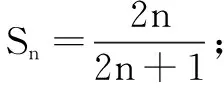
变式5已知an=(-1)n-1(2n-1)2,求数列{an}的前n项和Sn.

解易见Sn=(12-32)+(52-72)+…+(-1)n-1(2n-1)2=(1-3)(1+3)+(5-7)(5+7)+…+(-1)n-1(2n-1)2.

当n是奇数时,Sn=Sn-1+an=-2(n-1)2+(2n-1)2=2n2-1.

评注此题把f(n)换成(2n-1)2,题设中的(-1)n-1起到的作用是两个平方项作差,相邻两项可以用平方差公式运算,用并项求和法即可转化为等差数列的求和问题.当然,在解题细节上需要注意对n进行分类讨论.

评注此题对前面的与(-1)n有关的求和问题进行了推广,通项公式是分段函数型,其中的奇数项和偶数项是均匀分布的,学生很容易分清它们的项数,将问题转化为等差数列、等比数列求和问题.

变式7在数列{an}中,已知

其中k∈N，求{an}的前4n项和S4n.

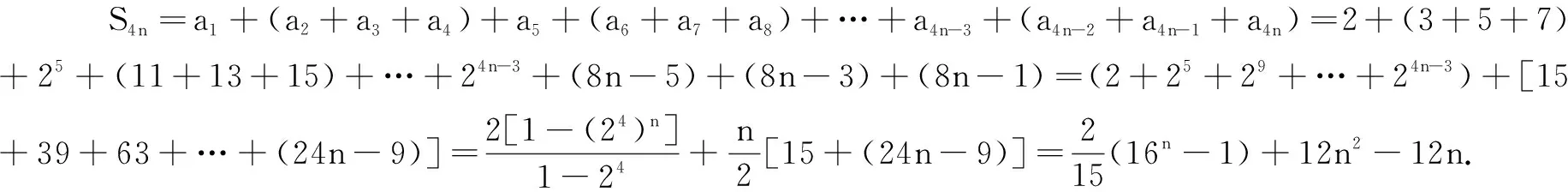
评注此题是分段函数中的不均匀分组,重新组合后分组求和,因为求的是S4n,所以比较容易求和.若改为求Sn,则难度偏大,需要仔细分析并进行分类讨论,数清各组的项数,有兴趣的同学课后不妨进一步探究.